Somewhat Homomorphic Encryption Craig Gentry and Shai Halevi

Somewhat Homomorphic Encryption Craig Gentry and Shai Halevi June 3, 2014 China Summer School on Lattices and Cryptography

Part 1: Homomorphic Encryption: Background, Applications, Limitations

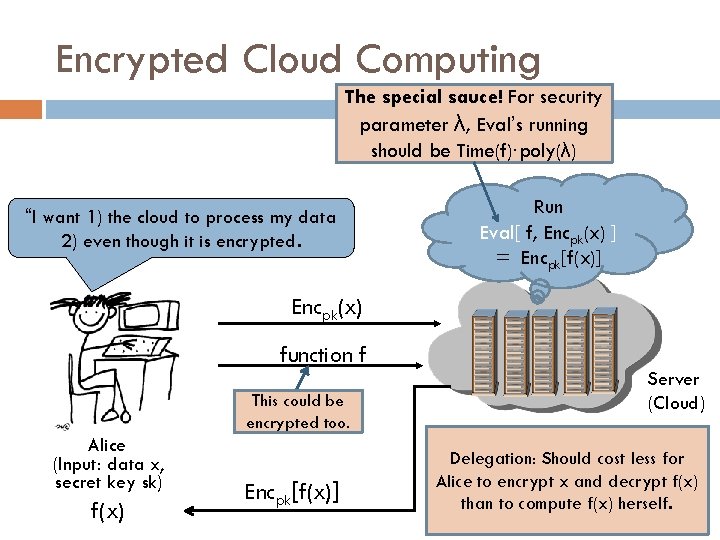
Computing on Encrypted Data Can we delegate the processing of data, without giving away access to it. Example App: Cloud computing Safe to store your data in the cloud unencrypted ? ?

Encrypted Cloud Computing The special sauce! For security parameter λ, Eval’s running should be Time(f)∙poly(λ) “I want 1) the cloud to process my data 2) even though it is encrypted. Run Eval[ f, Encpk(x) ] = Encpk[f(x)] Encpk(x) function f This could be encrypted too. Alice (Input: data x, secret key sk) f(x) Encpk[f(x)] Server (Cloud) Delegation: Should cost less for Alice to encrypt x and decrypt f(x) than to compute f(x) herself.

Homomorphic Encryption (HE) Procedures: Key. Gen, Encrypt, Decrypt, Eval Correctness: For any function f in “admissible” family F: c 1 ← Encpk(m 1) … ct ← Encpk(mt) c ← Evalpk(f, c 1, …, ct) Decsk(c) = f(m 1, …, mt) Semantic Security: same as for basic encryption

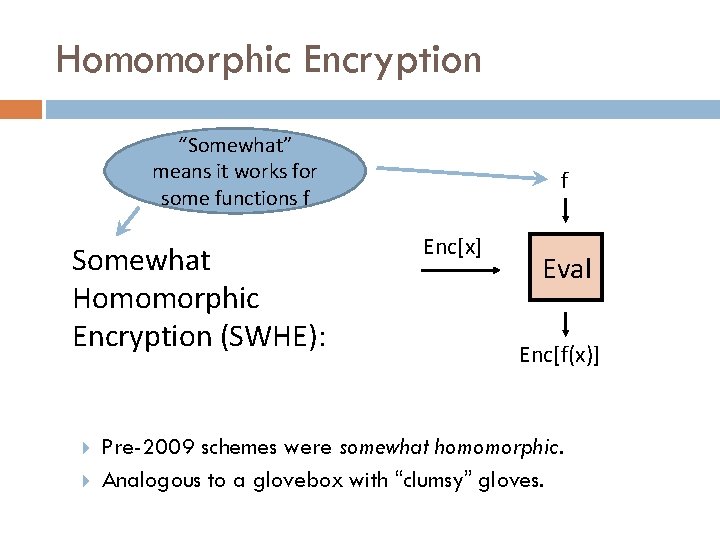
Homomorphic Encryption “Somewhat” means it works for some functions f Somewhat Homomorphic Encryption (SWHE): f Enc[x] Eval Enc[f(x)] Pre-2009 schemes were somewhat homomorphic. Analogous to a glovebox with “clumsy” gloves.

Homomorphic Encryption “Fully” means it works for all functions f Fully Homomorphic Encryption (FHE) [RAD 78, Gen 09]: f Enc[x] Eval Enc[f(x)]

Homomorphic Encryption Basics A way to delegate processing of your data, without giving away access to it. Fully Homomorphic Encryption (FHE): Arbitrary processing But computationally expensive. Somewhat Homomorphic Encryption (SWHE): Limited processing Cheaper computationally.

An Analogy: Alice’s Jewelry Store Alice wants workers to assemble raw materials into jewelry But Alice is worried about theft: She wants workers to process raw materials without having access. Alice puts raw materials in locked glovebox. Workers assemble jewelry inside glovebox, using the gloves. Alice unlocks box to get “results”.

Functionality

Processing (Unencrypted) Data Forget encryption for a moment… How does your compute a function? Basically, by working on bits, 1’s and 0’s. Using bit operations – for example, AND(b 1, b 2)=1 if b 1=b 2=1; otherwise, equals 0. AND(b 1, b 2)= b 1×b 2. XOR(b 1, b 2)=0 if b 1=b 2; equals 1 if b 1≠b 2. XOR(b 1, b 2)= b 1+b 2 (modulo 2)

Computing General Functions {ADD, MULT} are Turing-complete (over any ring). Take any (classically) efficiently computable function. Express it as a poly-size circuit of ADD and MULT gates. Circuits vs. Turing machines (about the same): Circuit size = O(Tf log Tf) Tf = time to compute f on a TM

Let’s Do This Encrypted… Let b denote a valid encryption of bit b.

Let’s Do This Encrypted… Let b denote a valid encryption of bit b. Suppose we have a (homomorphic) encryption scheme with public functions E-ADD, E-MULT where: E-MULT( b 1, b 2 ) = b 1 x b 2 E-ADD(b 1, b 2) = b 1+b 2 for any b 1 and b 2. Then we can AND and XOR encrypted bits. Proceeding bit-wise, we can compute any function on encrypted data.

Security

Security of Homomorphic Encryption Semantic security: For any m 0 ≠ m 1, (pk, Encpk(m 0)) (pk, Encpk(m 1)) means indistinguishable by efficient algorithms. Any semantically secure encryption scheme must be probabilistic – i. e. , many ciphertexts per plaintext.

HE Security: A Paradox? Cloud stores my encrypted files: pk, Encpk(f 1), …, Encpk(fn). Later, I want f 3, but want to hide “ 3” from cloud. I send Encpk (3) to the cloud. Cloud runs Evalpk (F, Encpk(3), Encpk(f 1), …, Encpk(fn)), where F(n, {files}) is the function that outputs the nth file. It sends me the (encrypted) file f 3. Paradox? : Can’t the cloud “see” it is sending the 3 rd encrypted file? By comparing the stored value Encpk(f 3) to the ciphertext it sends? Resolution of paradox: Semantic security implies: Ø Many encryptions of f 3, Ø Hard to tell when two ciphertexts encrypt the same thing.

Limitations

FHE Doesn’t Do Obfuscation: Difference between obfuscation and FHE: In FHE, cloud computes Enc(P(x)), and it can’t decrypt to get P(x). Barak et al: “On the (Im)possibility of Obfuscating Programs” I give the cloud an “encrypted” program Enc(P). For any input x, cloud can compute Enc(P)(x) = P(x). Cloud learns “nothing” about P, except {xi, P(xi)}. Certain types of obfuscation are impossible. Garg et al: “Candidate Indistinguishability Obfuscation and Functional Encryption for All Circuits” Certain types of obfuscation seem possible (we have schemes).

FHE Doesn’t Do RAM Circuits vs. RAMs: Circuits are powerful: Circuit-size ≈ TM complexity. But random-access machines compute some functions much faster than a TM or circuit (Binary search) Can’t do “random access” on encrypted data without leaking some information (not surprising) What we can do: Oblivious RAM: But this is a very interactive protocol between client and server where server can’t tell what client is computing Use Obfuscation to do ORAM: Intuitively, obfuscation allows addresses in memory to be revealed “noninteractively”.

FHE Doesn’t Do Multi-Key FHE Different clients encrypt data under different FHE keys. Later, cloud “combines” data encrypted under different keys: Encpk 1, …, pkt(f(m 1, …, mt)) ← Eval(pk 1, …pkt, f, c 1, …ct). FHE doesn’t do this “automatically”. But, “On-the-fly Multiparty Computation on the Cloud via Multikey FHE”: There is a scheme that does this.

Part 2: Somewhat Homomorphic Encryption Constructions

A Toy HE Scheme (from American Scientist magazine) Encryption: Double the plaintext. x → 2 x Decryption: Halve the ciphertext. x → x/2

Noisy Ciphertexts Each ciphertext has some noise that hides the message. Think: “hidden” error correcting codes… If error is small, Alice can use knowledge of “hidden” code to remove the noise. If noise is large, decryption is hopeless even for Alice.

Somewhat Homomorphic Encryption over the Integers The van Dijk, Gentry, Halevi, Vaikuntanathan scheme

SWHE with Integers Main Idea Encryptions of 0 are something small and even modulo a secret integer. Key. Gen: Secret key = large odd integer n. Public key: Integers q 1 n+2 r 1, …, qtn+2 rt with |ri| ¿ n. (These are encryptions of 0. ) Encrypt: Add a random subset of the encryptions of 0 to get a “random” encryption of 0. Then add the message m in {0, 1}. c = n(Σi in S qi) + 2(Σi in S ri) + m. Decrypt: Compute [c]n = m+smalleven. ([c]n denotes c mod n. ) Then, reduce mod 2 to get m. ADD and MULT: Output sum or product of ciphertexts.

Security of SWHE with Integers Reduction: “approximate gcd” problem is hard, then the scheme is semantically secure. If Approximate GCD Problem: Given many ai = ei + qi∙n (approx multiples of n), output n.

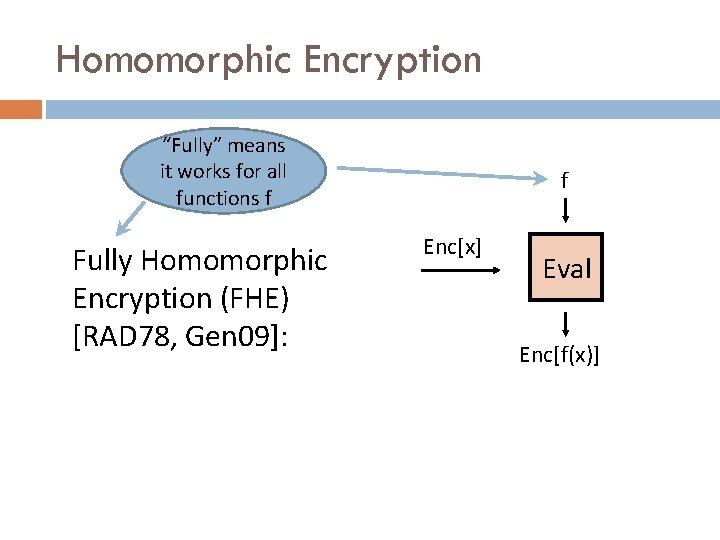
The Noise Problem ADD: c = c 1+c 2. Noise of c is [c]n = [c mod n] = sum of noises [c 1]n and [c 2]n. Unless this sum is bigger than n (decryption error). MULT: c = c 1∙c 2. Noise [c]n is product of noises, unless product > n. (q 1 n+e 1)∙(q 2 n+e 2) = (q 1 q 2 n+q 1 e 2+e 1 q 2)n + e 1 e 2. Function f: c = f(c 1, …, ct). [c]n = f([c 1]n, …, [ct]n) – i. e. , f applied to noises. Rough approximation: Noise magnitude increases exponentially with degree of f.

The Noise Problem Hurts Efficiency. Why? Ciphertexts must be large to let noise “room to grow”. Noise grows exponentially with degree. Bit-length of noise grows linearly with degree. Ciphertext size grows linearly with degree.

Somewhat Homomorphic Encryption Based on LWE Focusing on the Gentry-Sahai-Waters scheme. (Brakerski and Vaikuntanathan were the first to construct HE based on LWE. )

Recall Regev’s Encryption Scheme

Properties of Regev’s Scheme

Homomorphic ADD in Regev

Homomorphic MULT in Regev

Matrix Version of Regev st (1 Attempt)

Homomorphisms in Error-Free Setting Ciphertext Matrix Message Eigenvalue Secret Key Eigenvector

Homomorphisms with Error New Noise

Controlling the Noise New Noise

How to Flatten Ciphertexts

How to Flatten Ciphertexts

How to Flatten Ciphertexts

Flattening Ciphertexts Repeatedly

Key. Gen, Encrypt, and Decrypt

Security Based on LWE

Summary of GSW HE Scheme

Thank You! Questions? E M I T I RE D P X E ?

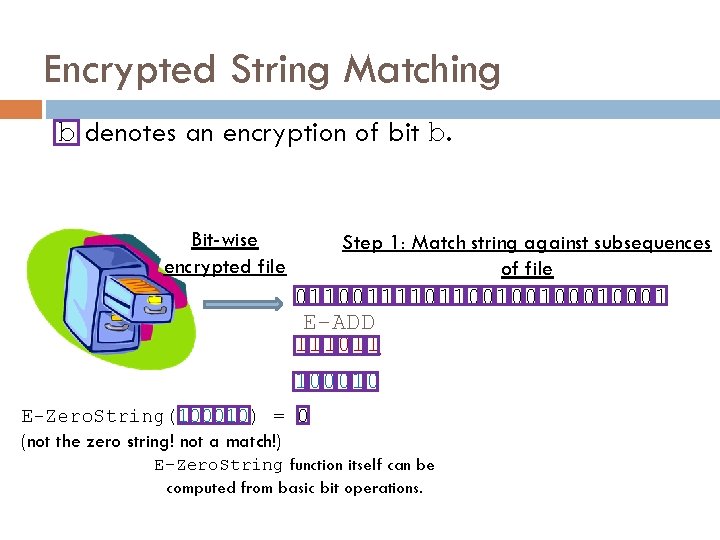
Encrypted String Matching b denotes an encryption of bit b. Bit-wise encrypted file Step 1: Match string against subsequences of file 0110011110110010010001 E-ADD 111011 100010 E-Zero. String(100010) = 0 (not the zero string! not a match!) E-Zero. String function itself can be computed from basic bit operations.

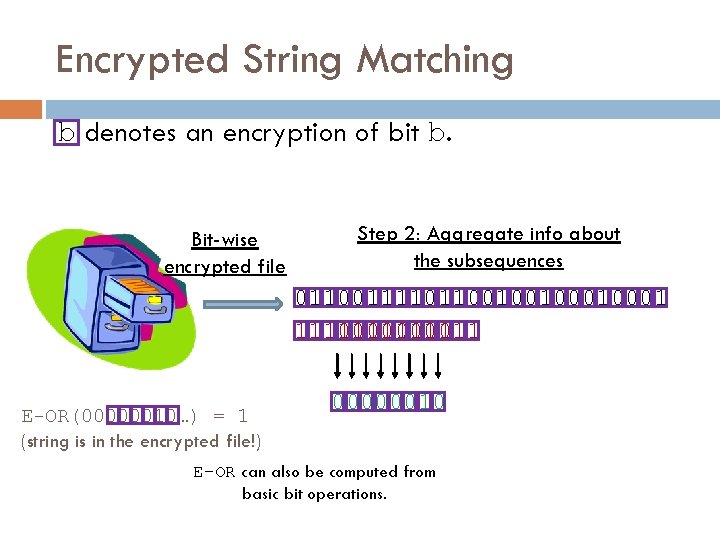
Encrypted String Matching b denotes an encryption of bit b. Bit-wise encrypted file Step 2: Aggregate info about the subsequences 0110011110110010010001 111011 111011 E-OR(00000010…) = 1 (string is in the encrypted file!) 00000010 E-OR can also be computed from basic bit operations.

Learning with Errors (LWE) Problem

Generalization of Error-Free Scheme (which is also insecure) Ciphertexts live in a ring RC. Plaintexts live in a ring RP. Decryption is a ring homomorphism Decsk: RC → RP. Homomorphic Eval operations: + and · in RC. Call it the “Hidden Ring Homomorphism Approach” Security: Ideal membership problem Is challenge ciphertext in the ideal of encryptions of 0?

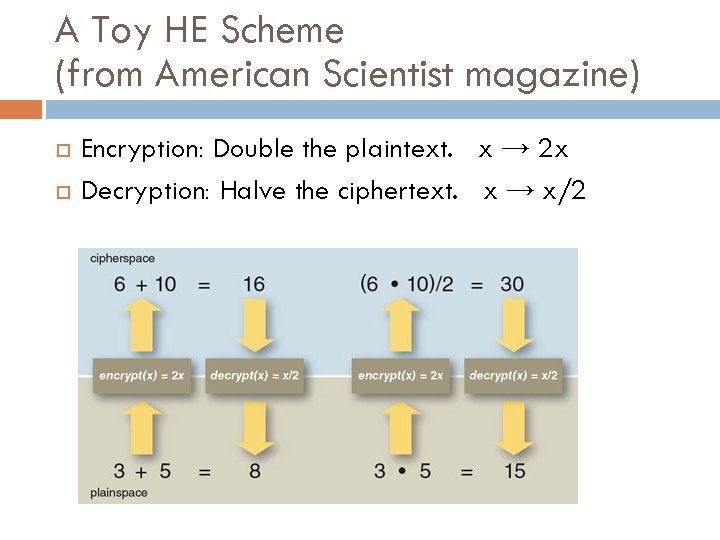
Polly Cracker [FK 93]: Ciphertexts in a multivariate polynomial ring Main Idea Encryptions of 0 are polynomials that evaluate to 0 at the secret key. Key. Gen: Secret sk = some point (s 1, …, st) 2 Zqt. Public key: Polynomials {fi(x 1, …, xt)} s. t. fi(s 1, …, st)=0 mod q. Encrypt: From {fi}, generate random poly g s. t. g(s 1, …, st) = 0 mod q. Ciphertext is c(x 1, …, xt) = μ + g(x 1, …, xt) mod q. Decrypt: Evaluate ciphertext at the secret: c(s 1, …, st) = μ mod q. ADD and MULT: Output sum or product of ciphertext polys. Security: Distinguish whether c has common root with the f i’s.

Polly Cracker Attack Collect lots of encryptions {ci} of 0. They form an ideal. The coefficient vectors of the ci’s generate a lattice L. Compute Hermite Normal Form (HNF) of L. Coefficient Else, vectors must be only polynomially long the scheme is inefficient Linear algebra attack on semantic security: To distinguish whether c encrypts 0 or 1, reduce it modulo HNF(L): the result will be 0 only if m = 0. Ideal membership problem is easy in this case.

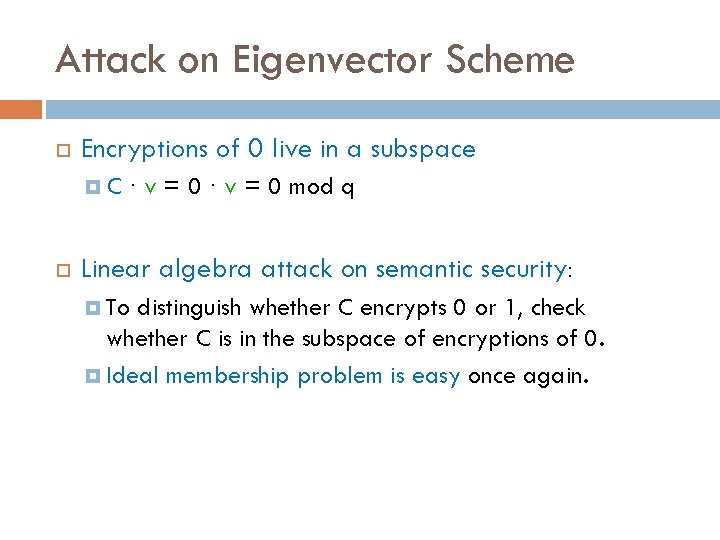
Attack on Eigenvector Scheme Encryptions of 0 live in a subspace C · v = 0 mod q Linear algebra attack on semantic security: To distinguish whether C encrypts 0 or 1, check whether C is in the subspace of encryptions of 0. Ideal membership problem is easy once again.

Identity-Based FHE (IBFHE)

IBE → IBFHE Compiler: What It Needs

IBE → IBFHE Compiler: Construction

Attribute-Based FHE (ABFHE)

Compiler: GVW ABE → ABFHE