Information Security Part II PublicKey Encryption and Hash

Information Security -- Part II Public-Key Encryption and Hash Functions Frank Yeong-Sung Lin Information Management Department National Taiwan University YSL Information Security -- Public-Key Cryptography

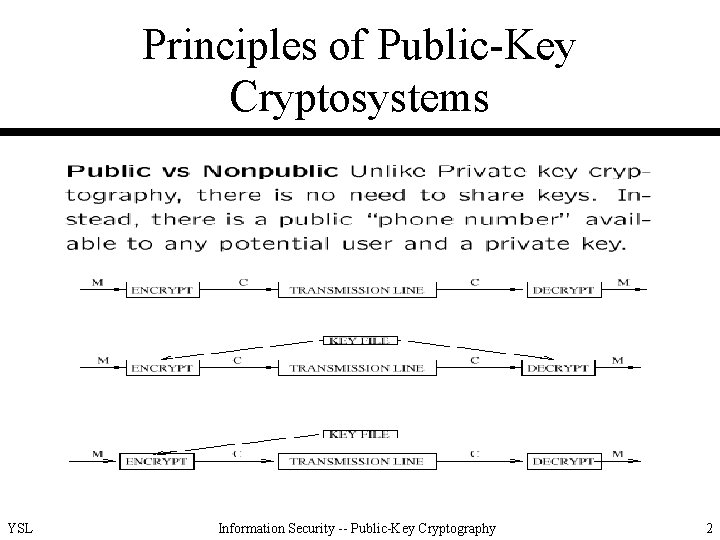
Principles of Public-Key Cryptosystems YSL Information Security -- Public-Key Cryptography 2

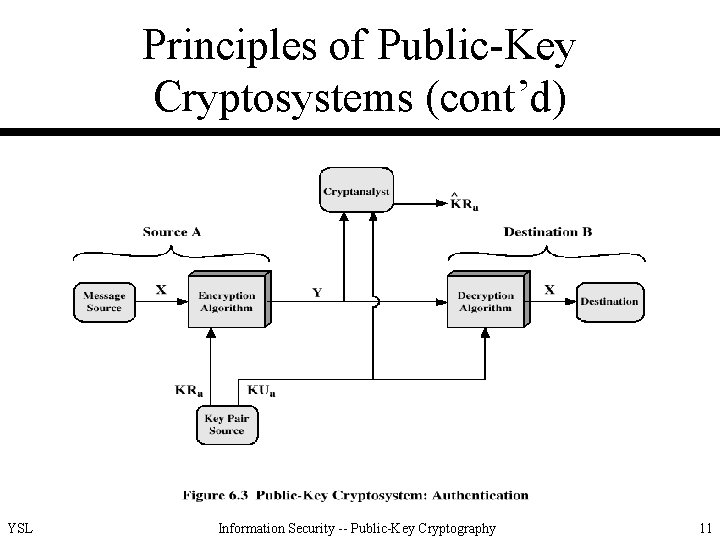
Principles of Public-Key Cryptosystems (cont’d) • Requirements for PKC – easy for B (receiver) to generate KUb and KRb – easy for A (sender) to calculate C = EKUb(M) – easy for B to calculate M = DKRb(C) = DKRb(EKUb(M)) – infeasible for an opponent to calculate KRb from KUb – infeasible for an opponent to calculate M from C and KUb – (useful but not necessary) M = DKRb(EKUb(M)) = EKUb(DKRb(M)) (true for RSA and good for authentication) YSL Information Security -- Public-Key Cryptography 3

Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 4

Principles of Public-Key Cryptosystems (cont’d) • The idea of PKC was first proposed by Diffie and Hellman in 1976. • Two keys (public and private) are needed. • The difficulty of calculating f -1 is typically facilitated by – factorization of large numbers – resolution of NP-completeness – calculation of discrete logarithms • High complexity confines PKC to key management and signature applications YSL Information Security -- Public-Key Cryptography 5

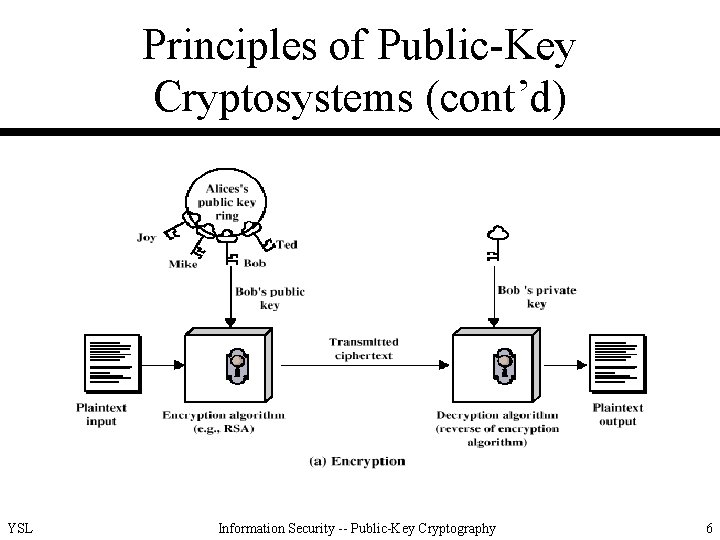
Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 6

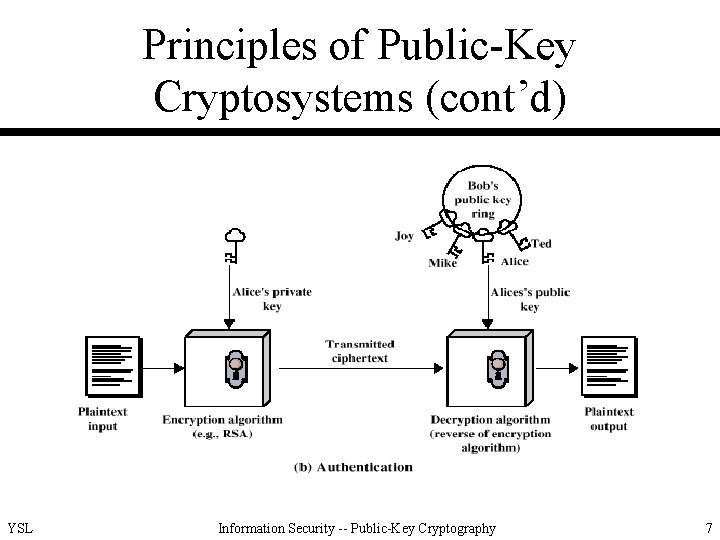
Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 7

Principles of Public-Key Cryptosystems (cont’d) • Comparison between conventional and public-key encryption YSL Information Security -- Public-Key Cryptography 8

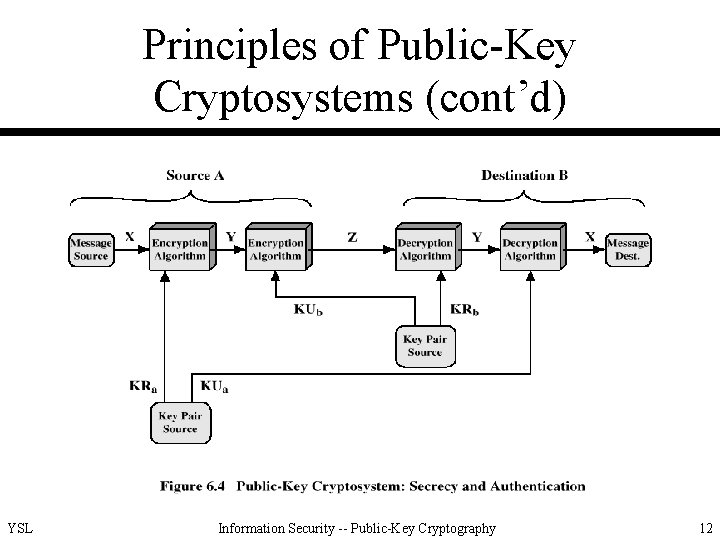
Principles of Public-Key Cryptosystems (cont’d) • Applications for PKC – encryption/decryption – digital signature – key exchange YSL Information Security -- Public-Key Cryptography 9

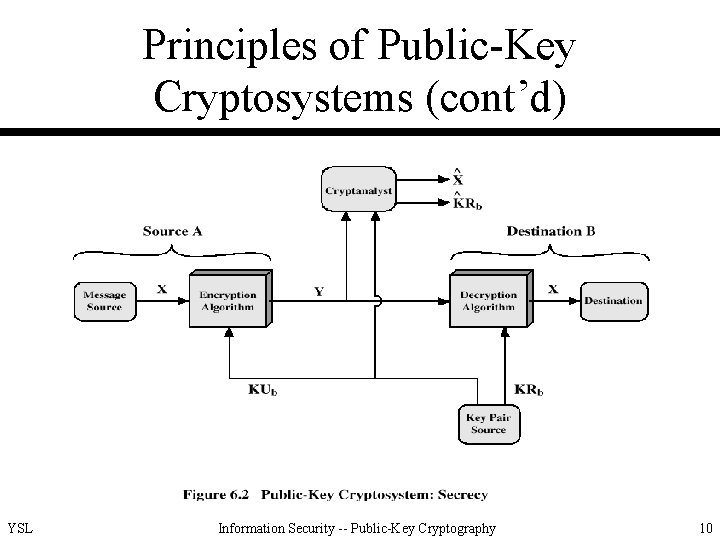
Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 10

Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 11

Principles of Public-Key Cryptosystems (cont’d) YSL Information Security -- Public-Key Cryptography 12

The RSA Algorithm • Developed by Rivest, Shamir, and Adleman at MIT in 1978 • First well accepted and widely adopted PKC algorithm • Security based on the difficulty of factoring large numbers • Patent expired in 2001 YSL Information Security -- Public-Key Cryptography 13

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 14

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 15

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 16

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 17

The RSA Algorithm (cont’d) Primes under 2000 YSL Information Security -- Public-Key Cryptography 18

The RSA Algorithm (cont’d) • The above statement is referred to as the prime number theorem, which was proven in 1896 by Hadaward and Poussin. YSL Information Security -- Public-Key Cryptography 19

The RSA Algorithm (cont’d) • Whethere exists a simple formula to generate prime numbers? • An ancient Chinese mathematician conjectured that if n divides 2 n - 2 then n is prime. For n = 3, 3 divides 6 and n is prime. However, For n = 341 = 11 31, n dives 2341 - 2. • Mersenne suggested that if p is prime then Mp = 2 p - 1 is prime. This type of primes are referred to as Mersenne primes. Unfortunately, for p = 11, M 11 = 211 -1 = 2047 = 23 89. YSL Information Security -- Public-Key Cryptography 20

The RSA Algorithm (cont’d) n • Fermat conjectured that if Fn = + 1, where n is a non-negative integer, then Fn is prime. When n is less than or equal to 4, F 0 = 3, F 1 = 5, F 2 = 17, F 3 = 257 and F 4 = 65537 are all primes. However, F 5 = 4294967297 = 641 6700417 is not a prime number. • n 2 - 79 n + 1601 is valid only for n < 80. • There an infinite number of primes of the form 4 n + 1 or 4 n + 3. • There is no simple way so far to gererate prime numbers. 22 YSL Information Security -- Public-Key Cryptography 21

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 22

The RSA Algorithm (cont’d) • Prime gap: displacement between two consecutive prime numbers – unbounded – n!+2, n!+3, n!+4, …, n!+n are not prime YSL Information Security -- Public-Key Cryptography 23

The RSA Algorithm (cont’d) • Format’s Little Theorem (to be proven later): If p is prime and a is a positive integer not divisible by p, then a p-1 1 mod p. Example: a = 7, p = 19 72 = 49 11 mod 19 74 = 121 7 mod 19 78 = 49 11 mod 19 716 = 121 7 mod 19 a p-1 = 718 = 716+2 7 11 1 mod 19 YSL Information Security -- Public-Key Cryptography 24

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 25

The RSA Algorithm (cont’d) • • • YSL A = M+ip for a non-negative integer i. A = M+jq for a non-negative integer j. From the above two equations, ip = jq. Then, i = kq. Consequently, A = M+ip = M+kpq. Q. E. D. (quod erat demonstrandum) Information Security -- Public-Key Cryptography 26

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 27

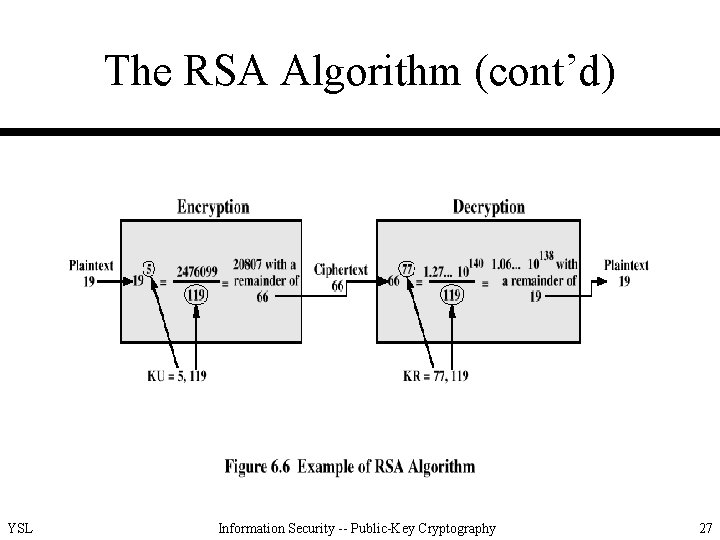
The RSA Algorithm (cont’d) • Example 1 – – Select two prime numbers, p = 7 and q = 17. Calculate n = p q = 7 17 = 119. Calculate Φ(n) = (p-1)(q-1) = 96. Select e such that e is relatively prime to Φ(n) = 96 and less than Φ(n); in this case, e = 5. – Determine d such that d e 1 mod 96 and d < 96. The correct value is d = 77, because 77 5 = 385 = 4 96+1. YSL Information Security -- Public-Key Cryptography 28

The RSA Algorithm (cont’d) • YSL Information Security -- Public-Key Cryptography 29

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 30

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 31

The RSA Algorithm (cont’d) • Key generation – determining two large prime numbers, p and q – selecting either e or d and calculating the other • Probabilistic algorithm to generate primes – [1] Pick an odd integer n at random. – [2] Pick an integer a < n at random. – [3] Perform the probabilistic primality test, such as Miller-Rabin. If n fails the test, reject the value n and go to [1]. – [4] If n has passed a sufficient number of tests, accept n; otherwise, go to [2]. YSL Information Security -- Public-Key Cryptography 32

The RSA Algorithm (cont’d) • How may trials on the average are required to find a prime? – from the prime number theory, primes near n are spaced on the average one every (ln n) integers – even numbers can be immediately rejected – for a prime on the order of 2200, about (ln 2200)/2 = 70 trials are required • To calculate e, what is the probability that a random number is relatively prime to Φ(n)? About 0. 6. YSL Information Security -- Public-Key Cryptography 33

The RSA Algorithm (cont’d) • For fixed length keys, how many primes can be chosen? – for 64 -bit keys, 264/ln 264 - 263/ln 263 2. 05 1017 – for 128 - and 256 -bit keys, 1. 9 1036 and 3. 25 1074, respectively, are available • For fixed length keys, what is the probability that a randomly selected odd number a is prime? – for 64 -bit keys, 2. 05 1017/(0. 5 (264 - 263)) 0. 044 (expectation value: 1/0. 044 23) – for 128 - and 256 -bit keys, 0. 022 and 0. 011, respectively YSL Information Security -- Public-Key Cryptography 34

The RSA Algorithm (cont’d) • The security of RSA – brute force: This involves trying all possible private keys. – mathematical attacks: There are several approaches, all equivalent in effect to factoring the product of two primes. – timing attacks: These depend on the running time of the decryption algorithm. YSL Information Security -- Public-Key Cryptography 35

The RSA Algorithm (cont’d) • To avoid brute force attacks, a large key space is required. • To make n difficult to factor – p and q should differ in length by only a few digits (both in the range of 1075 to 10100) – both (p-1) and (q-1) should contain a large prime factor – gcd(p-1, q-1) should be small – should avoid e << n and d < n 1/4 YSL Information Security -- Public-Key Cryptography 36

The RSA Algorithm (cont’d) • To make n difficult to factor (cont’d) – p and q should best be strong primes, where p is a strong prime if • there exist two large primes p 1 and p 2 such that p 1|p-1 and p 2|p+1 • there exist four large primes r 1, s 1, r 2 and s 2 such that r 1|p 1 -1, s 1|p 1+1, r 2|p 2 -1 and s 2|p 2+1 – e should not be too small, e. g. for e = 3 and C = M 3 mod n, if M 3 < n then M can be easily calculated YSL Information Security -- Public-Key Cryptography 37

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 38

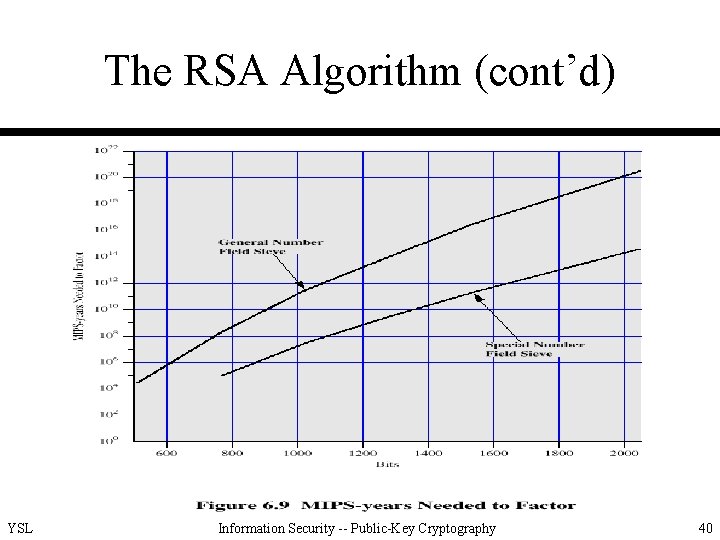
The RSA Algorithm (cont’d) • Major threats – the continuing increase in computing power (100 or even 1000 MIPS machines are easily available) – continuing refinement of factoring algorithms (from QS to GNFS and to SNFS) YSL Information Security -- Public-Key Cryptography 39

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 40

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 41

The RSA Algorithm (cont’d) YSL Information Security -- Public-Key Cryptography 42

Key Management • The distribution of public keys – public announcement – publicly available directory – public-key authority – public-key certificates • The use of public-key encryption to distribute secret keys – simple secret key distribution – secret key distribution with confidentiality and authentication YSL Information Security -- Public-Key Cryptography 43

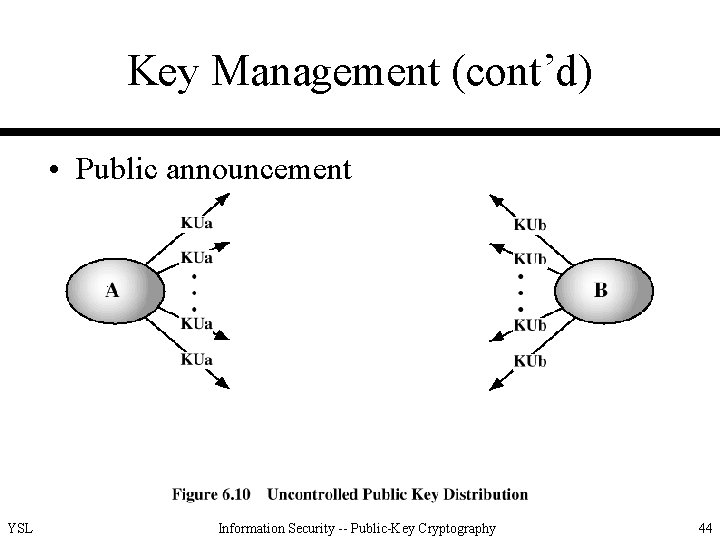
Key Management (cont’d) • Public announcement YSL Information Security -- Public-Key Cryptography 44

Key Management (cont’d) • Public announcement (cont’d) – advantages: convenience – disadvantages: forgery of such a public announcement by anyone YSL Information Security -- Public-Key Cryptography 45

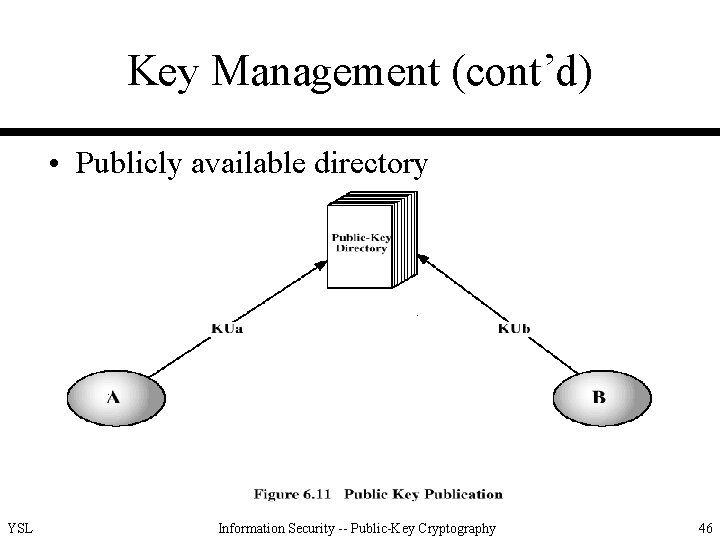
Key Management (cont’d) • Publicly available directory YSL Information Security -- Public-Key Cryptography 46

Key Management (cont’d) • Publicly available directory (cont’d) – elements of the scheme • {name, public key} entry for each participant in the directory • in-person or secure registration • on-demand entry update • periodic publication of the directory • availability of secure electronic access from the directory to participants – advantages: greater degree of security YSL Information Security -- Public-Key Cryptography 47

Key Management (cont’d) • Publicly available directory (cont’d) – disadvantages • need of a trusted entity or organization • need of additional security mechanism from the directory authority to participants • vulnerability of the private key of the directory authority (global-scaled disaster if the private key of the directory authority is compromised) • vulnerability of the directory records YSL Information Security -- Public-Key Cryptography 48

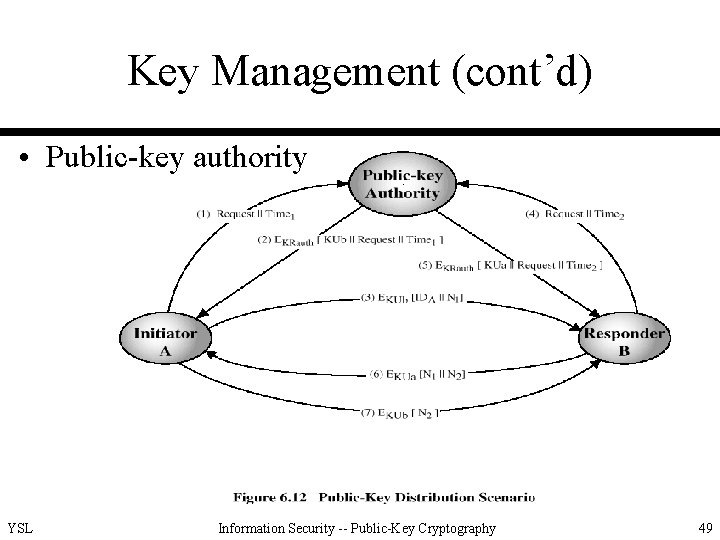
Key Management (cont’d) • Public-key authority YSL Information Security -- Public-Key Cryptography 49

Key Management (cont’d) • Public-key authority (cont’d) – stronger security for public-key distribution can be achieved by providing tighter control over the distribution of public keys from the directory – each participant can verify the identity of the authority – participants can verify identities of each other – disadvantages • bottleneck effect of the public-key authority • vulnerability of the directory records YSL Information Security -- Public-Key Cryptography 50

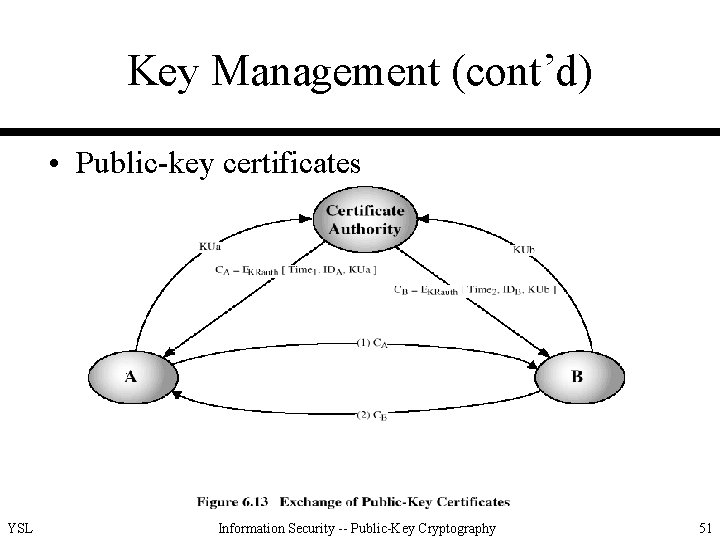
Key Management (cont’d) • Public-key certificates YSL Information Security -- Public-Key Cryptography 51

Key Management (cont’d) • Public-key certificates (cont’d) – to use certificates that can be used by participants to exchange keys without contacting a public-key authority – requirements on the scheme • any participant can read a certificate to determine the name and public key of the certificate’s owner • any participant can verify that the certificate originated from the certificate authority and is not counterfeit • only the certificate authority can create & update certificates • any participant can verify the currency of the certificate YSL Information Security -- Public-Key Cryptography 52

Key Management (cont’d) • Public-key certificates (cont’d) – advantages • to use certificates that can be used by participants to exchange keys without contacting a public-key authority • in a way that is as reliable as if the key were obtained directly from a public-key authority • no on-line bottleneck effect – disadvantages: need of a certificate authority YSL Information Security -- Public-Key Cryptography 53

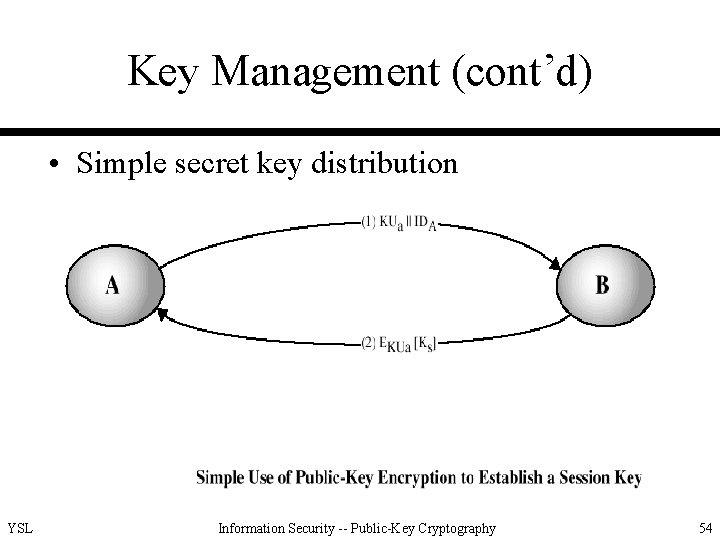
Key Management (cont’d) • Simple secret key distribution YSL Information Security -- Public-Key Cryptography 54

Key Management (cont’d) • Simple secret key distribution (cont’d) – advantages • simplicity • no keys stored before and after the communication • security against eavesdropping – disadvantages • lack of authentication mechanism between participants • vulnerability to an active attack (opponent active only in the process of obtaining Ks) • leak of the secret key upon such active attacks YSL Information Security -- Public-Key Cryptography 55

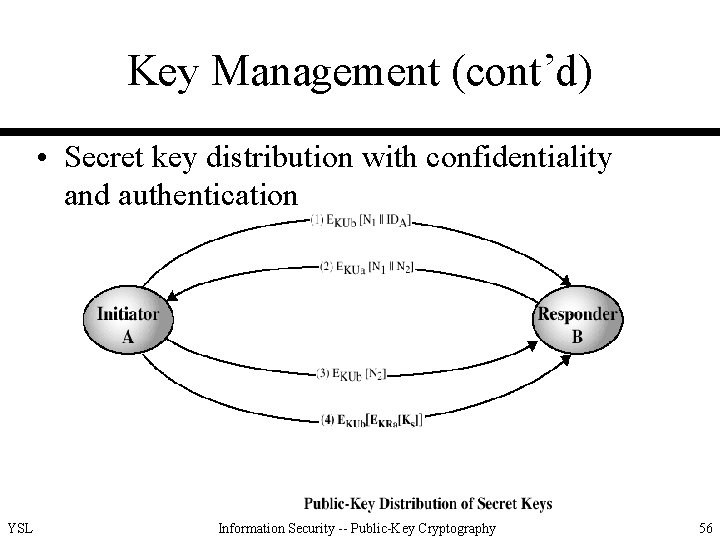
Key Management (cont’d) • Secret key distribution with confidentiality and authentication YSL Information Security -- Public-Key Cryptography 56

Key Management (cont’d) • Secret key distribution with confidentiality and authentication (cont’d) – provides protection against both active and passive attacks – ensures both confidentiality and authentication in the exchange of a secret key – public keys should be obtained a priori – more complicated YSL Information Security -- Public-Key Cryptography 57

Diffie-Hellman Key Exchange • First public-key algorithm published • Limited to key exchange • Dependent for its effectiveness on the difficulty of computing discrete logarithm YSL Information Security -- Public-Key Cryptography 58

Diffie-Hellman Key Exchange (cont’d) • Define a primitive root of of a prime number p as one whose powers generate all the integers from 1 to p-1. • If a is a primitive root of the prime number p, then the numbers a mod p, a 2 mod p, …, ap-1 mod p are distinct and consist of the integers from 1 to p-1 in some permutation. • Not every number has a primitive root. YSL Information Security -- Public-Key Cryptography 59

Diffie-Hellman Key Exchange (cont’d) • For any integer b and a primitive root a of prime number p, one can find a unique exponent i such that b = ai mod p, where 0 i (p-1). • The exponent i is referred to as the discrete logarithm, or index, of b for the base a, mod p. • This value is denoted as inda, p(b) (dloga, p(b)). YSL Information Security -- Public-Key Cryptography 60

Diffie-Hellman Key Exchange (cont’d) YSL Information Security -- Public-Key Cryptography 61

Diffie-Hellman Key Exchange (cont’d) • Example: q = 97 and a primitive root a = 5 is selected. XA = 36 and XB = 58 (both < 97). YA = 536 = 50 mod 97 and YB = 558 = 44 mod 97. K = (YB) X mod 97 = 4436 mod 97 = 75 mod 97. K = (YA) X mod 97 = 5058 mod 97 = 75 mod 97. 75 cannot easily be computed by the opponent. A B YSL Information Security -- Public-Key Cryptography 62

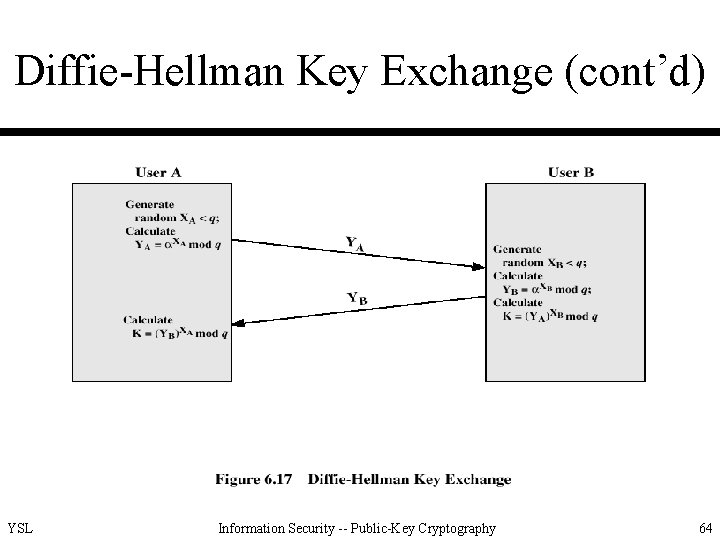
Diffie-Hellman Key Exchange (cont’d) • How the algorithm works YSL Information Security -- Public-Key Cryptography 63

Diffie-Hellman Key Exchange (cont’d) YSL Information Security -- Public-Key Cryptography 64

Diffie-Hellman Key Exchange (cont’d) • q, a, YA and YB are public. • To attack the secrete key of user B, the opponent must compute XB = inda, q(YB). [YB = a. X mod q. ] • The effectiveness of this algorithm therefore depends on the difficulty of solving discrete logarithm. B YSL Information Security -- Public-Key Cryptography 65

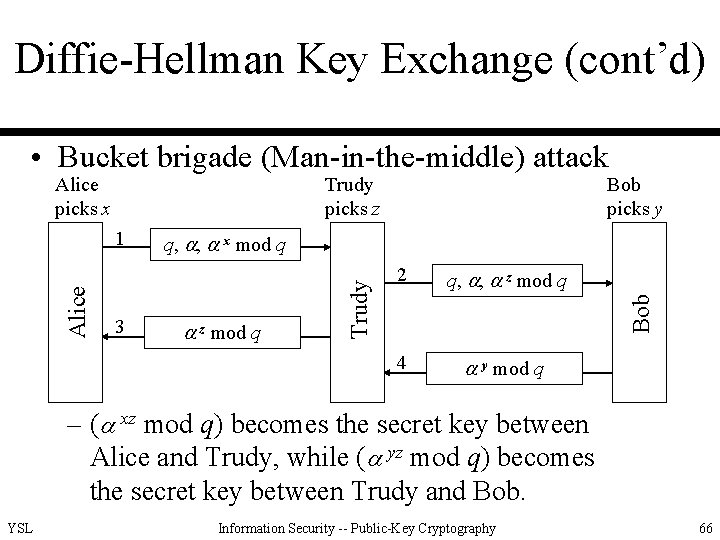
Diffie-Hellman Key Exchange (cont’d) • Bucket brigade (Man-in-the-middle) attack Alice picks x Trudy picks z z mod q 2 q, , z mod q 4 y mod q Bob 3 q, , x mod q Trudy Alice 1 Bob picks y – ( xz mod q) becomes the secret key between Alice and Trudy, while ( yz mod q) becomes the secret key between Trudy and Bob. YSL Information Security -- Public-Key Cryptography 66