Discrete Gaussian Leftover Hash Lemma Shweta Agrawal IIT

Discrete Gaussian Leftover Hash Lemma Shweta Agrawal IIT Delhi With Craig Gentry, Shai Halevi, Amit Sahai

Need Good Randomness 2 • Crucially need ideal randomness in many areas, eg. cryptography • However, often deal with imperfect randomness • physical sources, biometric data, partial knowledge about secrets… • Can we “extract” good randomness from ill-behaved random variables? Yes! EXTRACTORS (NZ 96)

Classic Leftover Hash Lemma Universal Hash Family H = { h: X Y } For all x ≠ y Prh [ h(x) = h(y) ] = 1/|Y| Leftover Hash Lemma (HILL) : Universal hash functions yield good extractors ( h(x), h) ≈ (U, h)

Classic use of LHL Universal Hash Function : Inner Product over finite field H = { h a: Z qm Z q } Pick a 1…. . am uniformly over Zq Define ha(x) = Σ ai xi mod q ha(x) uniform over Zq Simple, useful randomness extractor !

Discrete Gaussian LHL ? What if target distribution we need is discrete Gaussian instead of uniform? What if domain is infinite ring instead of finite field? When do generalized subset sums of lattice points yield nice discrete Gaussians ?

You ask … What are discrete Gaussians ? Why do we care ?

Why do we care ? Because they help us build “Multilinear Maps” from lattices (GGH 12)!

WHAT ARE DISCRETE GAUSSIANS?

Lattices… v’ 2 v’ 1 v 2 A set of points with periodic arrangement Discrete subgroup in Rn

What are discrete Gaussians ? DΛ, r : Gaussian distribution with std deviation r but support restricted to points over lattice Λ More formally …. . DΛ, r (x) α exp(-Π ||x||2 / r 2) if x in Λ 0 otherwise

Why study discrete Gaussians ? • Ubiquitous in lattice based crypto • At the technical core of most proofs in the area, notably in the famous “Learning with Errors” assumption • Not as well understood as their continuous counterparts

Our Results: Discrete Gaussian LHL over infinite domains • Fix once and for all, vectors x 1…. . xm Λ • We choose xi from discrete Gaussian DΛ, s • Let X = [x 1|…. . |xm] Zn x m • Choose vector z from discrete Gaussian DZm, s’ • Then the distribution Σ zi xi is statistically close to DΛ, s’X • DΛ, s’X is a “roughly spherical” discrete Gaussian of “moderate width” (under certain conditions)

Oblivious Gaussian Sampler • Our result yields an oblivious Gaussian sampler: • Given enc(x 1)…. . enc(xm) • If enc is additively homomorphic, can compute enc(g) where g is discrete Gaussian. • Just sample z and compute Σ zi enc(xi) • Previous Gaussian samplers [GPV 08, Pei 10] too complicated to use within additively homomorphic scheme.

Why is the Gaussian LHL true ?

Analyzing Σ zi xi : Proof Idea Recall our setup: • Fix once and for all, vectors x 1…. . xm Λ • We sample xi from discrete Gaussian DΛ, s nxm Let X = [x |…. . |x ] Z 1 m • • Sample vector z from discrete Gaussian DZm, s’ Define A = {v Zm : X v = 0} Note, A is a lattice.

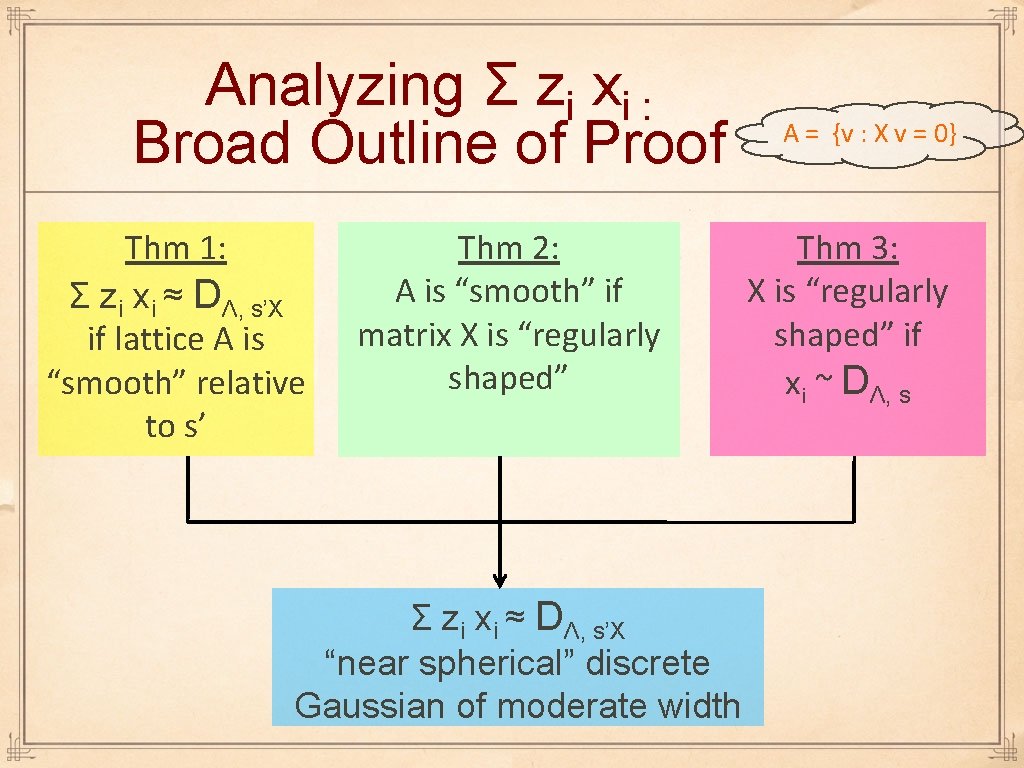
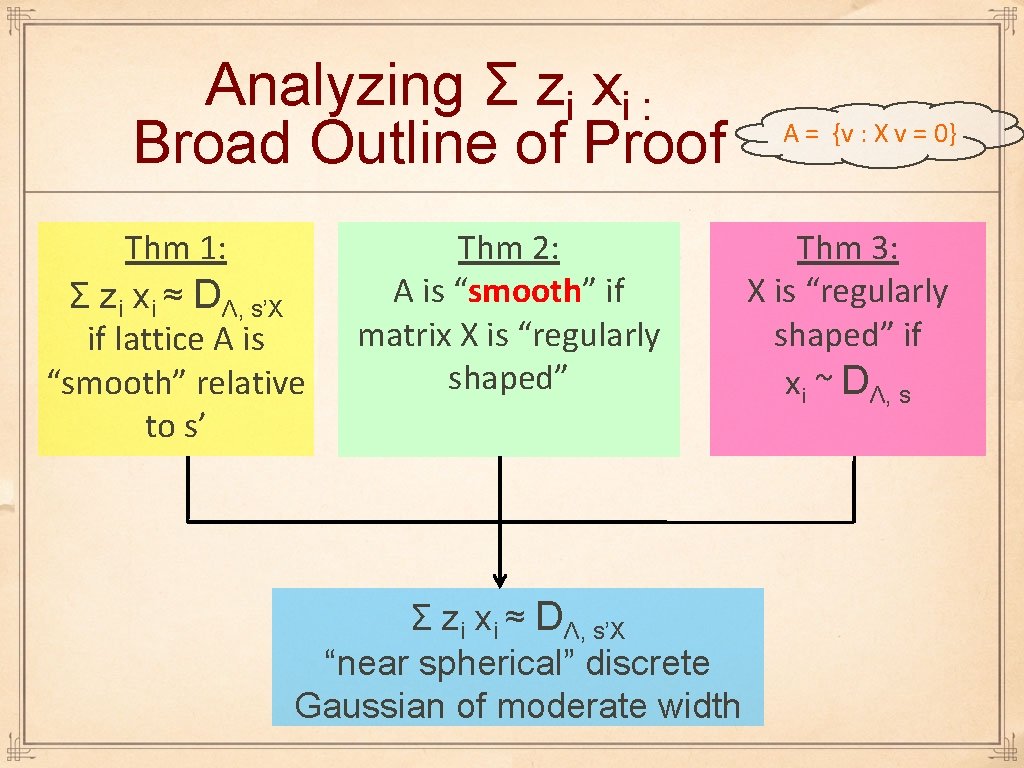
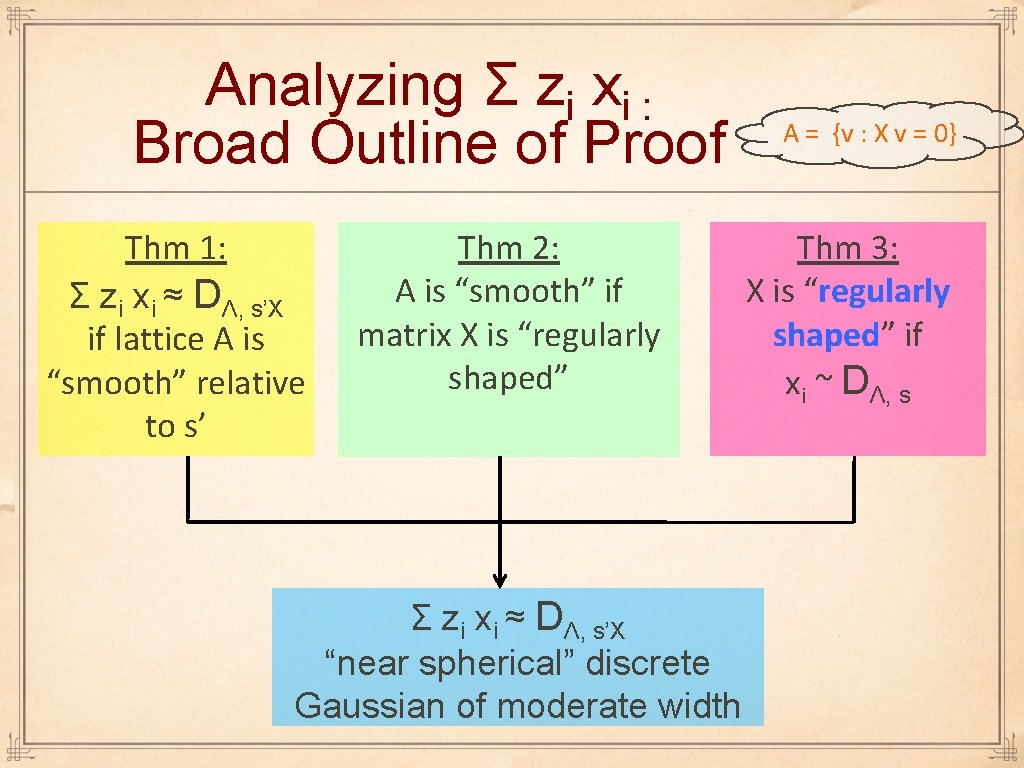
Analyzing Σ zi xi : Broad Outline of Proof Thm 1: Σ zi xi ≈ DΛ, s’X if lattice A is “smooth” relative to s’ Thm 2: A is “smooth” if matrix X is “regularly shaped” Σ zi xi ≈ DΛ, s’X “near spherical” discrete Gaussian of moderate width A = {v : X v = 0} Thm 3: X is “regularly shaped” if xi ~ DΛ, s

Analyzing Σ zi xi : Broad Outline of Proof Thm 1: Σ zi xi ≈ DΛ, s’X if lattice A is “smooth” relative to s’ Thm 2: A is “smooth” if matrix X is “regularly shaped” Σ zi xi ≈ DΛ, s’X “near spherical” discrete Gaussian of moderate width A = {v : X v = 0} Thm 3: X is “regularly shaped” if xi ~ DΛ, s

Analyzing Σ zi xi : Broad Outline of Proof Thm 1: Σ zi xi ≈ DΛ, s’X if lattice A is “smooth” relative to s’ Thm 2: A is “smooth” if matrix X is “regularly shaped” Σ zi xi ≈ DΛ, s’X “near spherical” discrete Gaussian of moderate width A = {v : X v = 0} Thm 3: X is “regularly shaped” if xi ~ DΛ, s

Smoothness of a Lattice Want to wipe out the structure of the lattice Add noise to lattice points till we get the uniform distribution * Smoothness animation from Regev’s slides

Smoothness of a Lattice Want to wipe out the structure of the lattice Add noise to lattice points till we get the uniform distribution * Smoothness animation from Regev’s slides

Smoothness of a Lattice Want to wipe out the structure of the lattice Add noise to lattice points till we get the uniform distribution * Smoothness animation from Regev’s slides

Smoothness of a Lattice Want to wipe out the structure of the lattice Add noise to lattice points till we get the uniform distribution * Smoothness animation from Regev’s slides

Smoothness of a Lattice How much noise is needed to blur the lattice depends on its structure Informally, if the noise magnitude needed is “small”, we may say that a lattice is “smooth” Measured by smoothing parameter smooth(L) [MR 04] Smooth(L) is the smallest “s” s. t. adding Gaussian noise of radius s to L yields an essentially uniform distribution

“ Regularly shaped” X is regularly shaped if its singular values lie within small interval. Thm 3: If xi ~ DΛ, s then X is regularly shaped Start with random matrix theory. Know that if matrix M has continuous Gaussian entries and m >2 n, then all the singular values of M are within constant sized interval Can extend this to discrete Gaussians,

Broad Outline of Proof Thm 1: Σ zi xi ≈ DΛ, s’X if s’ > smooth(A) Thm 2: If matrix X is “regularly shaped” then smooth(A) is small. Σ zi xi ≈ DΛ, s’X “near spherical” discrete Gaussian of moderate width Thm 3: If xi ~ DΛ, s then X is “regularly shaped”

Thm 2: smooth(A) is small if X is regularly shaped. Embed A into a full rank lattice Aq Consider dual lattice Mq : dual of Aq Argue that λn+1(Mq), the (n+1)st minima of Mq is large if X regularly shaped Convert to upper bound λm-n(Aq) using thm by Banasczcyk Argue these m-n short vectors belong to A Relate λm-n(A) to smooth(A) using bound by MR 04

Applicability Typical application would use our LHL to drown out some value it wishes to hide, a la GGH 12. Need the minimum width of the Gaussian to be wide enough to drown out the value it is hiding Our LHL can be seen as showing that this can be done in a frugal way, without wasting too many samples. Can be used within additively homomorphic scheme. Care needs to be taken if basis X has to be kept secret. Better use other samplers (GPV 08, Pei 10)

Conclusions Provided a discrete Gaussian LHL over infinite rings. May be used as an oblivious Gaussian sampler within an additively homomorphic scheme. Discrete Gaussians are important and not as well understood. Our work makes progress towards understanding their behavior.

Thank you! Questions?