Prerequisites Almost essential Firm Optimisation Consumption Basics CONSUMER

Prerequisites Almost essential Firm: Optimisation Consumption: Basics CONSUMER OPTIMISATION MICROECONOMICS Principles and Analysis Frank Cowell April 2018 Frank Cowell: Consumer Optimisation 1

What we’re going to do: § We’ll solve the consumer's optimisation problem • using methods that we've already introduced § This enables us to re-cycle old techniques and results § A tip: • check the presentation for firm optimisation • look for the points of comparison • try to find as many reinterpretations as possible April 2018 Frank Cowell: Consumer Optimisation 2

The problem § Maximise consumer’s utility U(x) U assumed to satisfy the standard “shape” axioms § Subject to feasibility constraint Assume consumption set X is the non-negative orthant § and to the budget constraint The version with fixed money income x X n S pixi ≤ y i=1 April 2018 Frank Cowell: Consumer Optimisation 3

Overview Consumer: Optimisation Two fundamental views of consumer optimisation Primal and Dual problems Lessons from the Firm Primal and Dual again April 2018 Frank Cowell: Consumer Optimisation 4

An obvious approach? § We have the elements of a standard constrained optimisation problem: • the constraints on the consumer • the objective function § The next steps might seem obvious: • set up a standard Lagrangian • solve it • interpret the solution § But the obvious approach is not always the most useful • we will use a round-about approach • generates extra insights • enables connection with theory of the firm April 2018 Frank Cowell: Consumer Optimisation 5

Think laterally § In microeconomics an optimisation problem can often be represented in more than one form § Which form you use depends on • your interpretation of the problem • the information you want to get from the solution § This applies here § The same consumer optimisation problem can be seen in two different ways 1. “primal problem” 2. “dual problem” • standard labels in the literature April 2018 Frank Cowell: Consumer Optimisation 6

A five-point plan 1. Set out the basic consumer optimisation problem • the primal problem 2. Show that the solution is equivalent to another problem • the dual problem 3. Show that this problem is identical to that of the firm 4. Write down the solution • copy directly from the solution to the firm’s problem 5. Go back to the problem we first thought of • the primal problem again April 2018 Frank Cowell: Consumer Optimisation 7

The primal problem x 2 § The consumer aims to maximise utility… § Subject to budget constraint Contours of objective function § Defines the primal problem § Solution to primal problem ing s a e re inc ferenc pre Constraint set max U(x) subject to l n x* S pi xi y i=1 x 1 April 2018 §There's another way of looking at this Frank Cowell: Consumer Optimisation 8

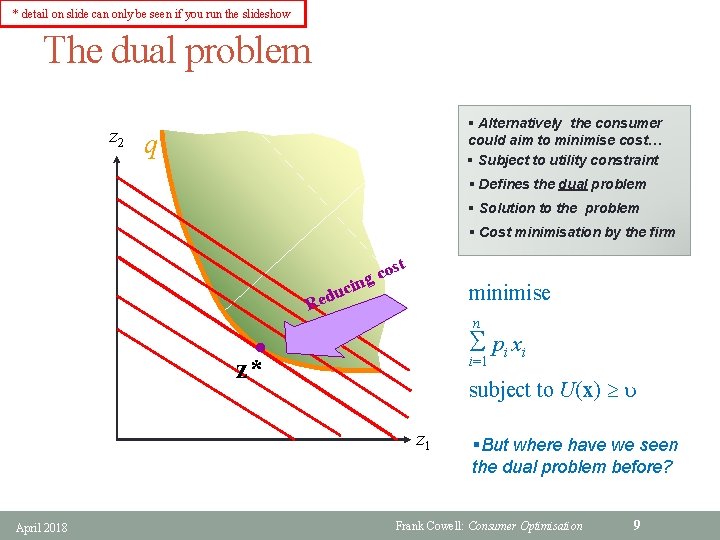
* detail on slide can only be seen if you run the slideshow The dual problem z 2 x 2 q u § Alternatively the consumer could aim to minimise cost… § Subject to utility constraint Constraint set § Defines the dual problem § Solution to the problem § Cost minimisation by the firm l l st o c ing c u t Red ng cos uci d e R minimise n S pi xi x* z* i=1 subject to U(x) u z 1 x 1 April 2018 §But where have we seen the dual problem before? Frank Cowell: Consumer Optimisation 9

Two types of cost minimisation § The similarity between the two problems is not just a curiosity § We can use it to save ourselves work § All the results that we had for the firm's “stage 1” problem can be used § We just need to “translate” them intelligently • Swap over the symbols • Swap over the terminology • Relabel theorems April 2018 Frank Cowell: Consumer Optimisation 10

Overview Consumer: Optimisation Reusing results on optimisation Primal and Dual problems Lessons from the Firm Primal and Dual again April 2018 Frank Cowell: Consumer Optimisation 11

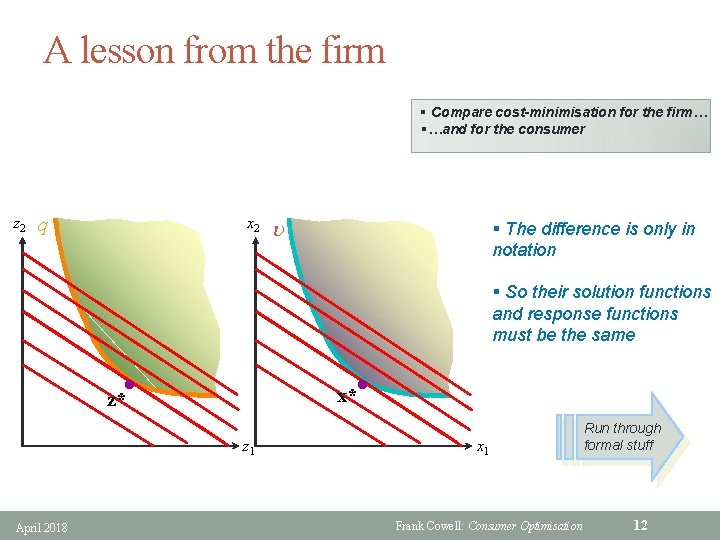
A lesson from the firm § Compare cost-minimisation for the firm… §…and for the consumer z 2 q x 2 u § The difference is only in notation § So their solution functions and response functions must be the same l l x* z* z 1 April 2018 x 1 Frank Cowell: Consumer Optimisation Run through formal stuff 12

Cost-minimisation: strictly quasiconcave U § Minimise n S pi xi i=1 § Use the objective function §…and utility constraint §…to build the Lagrangian Lagrange multiplier + λ[u – U(x)] u U(x) § Because of strict quasiconcavity we have an interior solution § Differentiate w. r. t. x 1, …, xn and set equal to 0 § … and w. r. t l § Denote cost minimising values with a * § A set of n + 1 First-Order Conditions l* U 1 (x* ) = p 1 one for each good l* U 2 (x* ) = p 2 … … … l* Un (x* ) = pn ü ý þ u = U(x* ) April 2018 utility constraint Frank Cowell: Consumer Optimisation 13

If ICs can touch the axes… § Minimise n S pixi i=1 + l[u – U(x)] § Now there is the possibility of corner solutions § A set of n + 1 First-Order Conditions April 2018 l*U 1 (x*) p 1 l*U 2 (x*) p 2 … … … l*Un(x*) pn ü ý þ u = U(x*) Can get “<” if optimal value of this good is 0 Interpretation Frank Cowell: Consumer Optimisation 14

From the FOC § If both goods i and j are purchased and MRS is defined then… Ui (x*) pi ——— = — * Uj (x ) pj § MRS = price ratio § “implicit” price = market price § If good i could be zero then… Ui (x*) pi ——— — * Uj (x ) pj § MRSji price ratio § “implicit” price market price Solution April 2018 Frank Cowell: Consumer Optimisation 15

The solution… § Solving the FOC, get a cost-minimising value for each good… xi* = Hi(p, u) § …for the Lagrange multiplier l* = l*(p, u) § …and for the minimised value of cost itself § The consumer’s cost function or expenditure function is defined as C(p, u) : = min S pi xi {U(x) u} vector of goods prices April 2018 Specified utility level Frank Cowell: Consumer Optimisation 16

The cost function has the same properties as for the firm § Non-decreasing in every price, increasing in at least one price § Increasing in utility u § Concave in p § Homogeneous of degree 1 in all prices p § Shephard's lemma April 2018 Frank Cowell: Consumer Optimisation 17

Other results follow § Shephard's Lemma gives H is the “compensated” or demand as a function of prices conditional demand function and utility Hi(p, u) = Ci(p, u) § Downward-sloping with respect Properties of the solution function determine behaviour to its own price, etc… of response functions § For example rationing “Short-run” results can be used to model side constraints April 2018 Frank Cowell: Consumer Optimisation 18

Comparing firm and consumer § § Cost-minimisation by the firm… …and expenditure-minimisation by the consumer …are effectively identical problems So the solution and response functions are the same: Consumer Firm m n min S wizi + l[q – f (z)] min S pixi + l[u – U(x)] § Solution function: C(w, q) C(p, u) § Response function: zi* = Hi(w, q) xi* = Hi(p, u) § Problem: z April 2018 i=1 x i=1 Frank Cowell: Consumer Optimisation 19

Overview Consumer: Optimisation Exploiting the two approaches Primal and Dual problems Lessons from the Firm Primal and Dual again April 2018 Frank Cowell: Consumer Optimisation 20

The Primal and the Dual… § There’s an attractive symmetry about the two approaches to the problem § In both cases the ps are given and you choose the xs § But constraint in the primal becomes objective in the dual… n S pixi+ l [u – U(x)] i=1 [ n U(x) + m y – S pi xi i=1 ] § …and vice versa April 2018 Frank Cowell: Consumer Optimisation 21

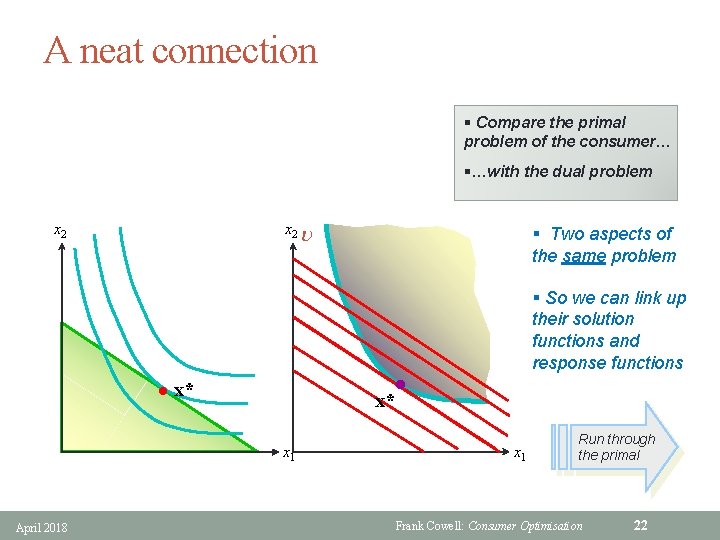
A neat connection § Compare the primal problem of the consumer… §…with the dual problem x 2 u § Two aspects of the same problem § So we can link up their solution functions and response functions l l x* x* x 1 April 2018 x 1 Run through the primal Frank Cowell: Consumer Optimisation 22

Utility maximisation § Maximise [ Lagrange multiplier nn – Spi xi U(x) + μ y i=1 ] § Use the objective function §…and budget constraint §…to build the Lagrangian § Differentiate w. r. t. x 1, …, xn and set equal to 0 § … and w. r. t m § If U is strictly quasiconcave we have § Denote utility maximising values with a * an interior solution § A set of n+1 First-Order one for. Conditions each good U 1(x* ) = m*p 1 U 2(x* ) = m*p 2 If U not strictly quasiconcave then … … … replace “=” by “ ” * * budget Un(x ) = m pn constraint n y = S pi xi* ü ý þ Interpretation i=1 April 2018 Frank Cowell: Consumer Optimisation 23

From the FOC § If both goods i and j are purchased and MRS is defined then… Ui (x*) pi ——— = — * Uj (x ) pj § MRS = price ratio §(same as before) § “implicit” price = market price § If good i could be zero then… Ui (x*) pi ——— — * Uj (x ) pj § MRSji price ratio § “implicit” price market price Solution April 2018 Frank Cowell: Consumer Optimisation 24

The solution… § Solving the FOC, you get a utility-maximising value for each good… xi* = Di(p, y) § …for the Lagrange multiplier m* = m*(p, y) § …and for the maximised value of utility itself § The indirect utility function is defined as V(p, y) : = max U(x) {S pixi y} vector of goods prices April 2018 money income Frank Cowell: Consumer Optimisation 25

A useful connection § The indirect utility function maps The indirect utility function works prices and budget into max utility like an "inverse" to the cost u = V(p, y) § The cost function maps prices and utility into min budget y = C(p, u) § Therefore we have: u = V(p, C(p, u)) y = C(p, V(p, y)) April 2018 function The two solution functions have to be consistent with each other. Two sides of the same coin Odd-looking identities like these can be useful Frank Cowell: Consumer Optimisation 26

The Indirect Utility Function has some familiar properties… (All of these can be established using the known properties of the cost function) § Non-increasing in every price, decreasing in at least one price § Increasing in income y § quasi-convex in prices p § Homogeneous of degree zero in (p, y) § Roy's Identity April 2018 Explanation of Roy’s Identity Frank Cowell: Consumer Optimisation 27

Roy's Identity u = V(p, y)= V(p, C(p, u)) “function-of-afunction” rule 0 = Vi (p, C(p, u)) + Vy (p, C(p, u)) Ci (p, u) § Use the definition of the optimum § Differentiate w. r. t. pi § Use Shephard’s Lemma § Rearrange to get… 0 = Vi (p, y) + Vy (p, y) x i* § So we also have… Marginal disutility of price i Vi (p, y) xi* = – ———— Vy (p, y) Marginal utility of money income Ordinary demand function xi* = –Vi (p, y)/Vy (p, y) = Di(p, y) April 2018 Frank Cowell: Consumer Optimisation 28

Utility and expenditure § § Utility maximisation …and expenditure-minimisation by the consumer …are effectively two aspects of the same problem So their solution and response functions are closely connected: Primal Dual [ n § Problem: max U(x) + μ y – Spi xi x § Solution function: V(p, y) § Response x * = Di(p, y) function: i April 2018 i=1 ] n min S pixi + l[u – U(x)] x i=1 C(p, u) xi* = Hi(p, u) Frank Cowell: Consumer Optimisation 29

Summary § A lot of the basic results of the consumer theory can be found without too much hard work § We need two “tricks”: 1. A simple relabelling exercise: • cost minimisation is reinterpreted from output targets to utility targets 2. The primal-dual insight: • utility maximisation subject to budget is equivalent to cost minimisation subject to utility April 2018 Frank Cowell: Consumer Optimisation 30

1. Cost minimisation: two applications § THE FIRM § THE CONSUMER § min cost of inputs § min budget § subject to output target § subject to utility target § Solution is of the form C(w, q) § Solution is of the form C(p, u) April 2018 Frank Cowell: Consumer Optimisation 31

2. Consumer: equivalent approaches n PRIMAL § DUAL n max utility § min budget subject to budget constraint § subject to utility constraint Solution is a function of (p, y) § Solution is a function of (p, u) n n April 2018 Frank Cowell: Consumer Optimisation 32

Basic functional relations Utility § C(p, u) § cost (expenditure) H is also known as "Hicksian" demand compensated demand for i H (p, u) good i § V(p, y) indirect utility § Di(p, y) ordinary demand for input i money income April 2018 Frank Cowell: Consumer Optimisation 33

What next? § Examine the response of consumer demand to changes in prices and incomes § Household supply of goods to the market § Develop the concept of consumer welfare April 2018 Frank Cowell: Consumer Optimisation 34