Prerequisites Almost essential Consumption Basics Frank Cowell Microeconomics

Prerequisites Almost essential Consumption: Basics Frank Cowell: Microeconomics November 2006 Consumption and Uncertainty MICROECONOMICS Principles and Analysis Frank Cowell

Why look again at preferences. . . Frank Cowell: Microeconomics n Aggregation issues u n Modelling specific economic problems u u n labour supply savings New concepts in the choice set u n restrictions on structure of preferences for consistency over consumers uncertainty Uncertainty extends consumer theory in interesting ways

Overview. . . Frank Cowell: Microeconomics Consumption: Uncertainty Modelling uncertainty Issues concerning the commodity space Preferences Expected utility The felicity function

Uncertainty Frank Cowell: Microeconomics New concepts n Fresh insights on consumer axioms n Further restrictions on the structure of utility functions n

Story Concepts Frank Cowell: Microeconomics American example If the only uncertainty is about who will be in power for the next four years then we might have states-of-the -world like this n § n pay-off (outcome) § W={Rep, Dem, Independent} xw X an array of bundles over the entire space W British example If the only uncertainty is about the weather then we might have states-ofthe-world like this w W a consumption bundle W={Rep, Dem} or perhaps like this: state-of-the-world n prospects § {xw : w W} n ex ante § before the realisation n ex post § after the realisation W={rain, sun} or perhaps like this: W={rain, drizzle, fog, sleet, hail. . . }

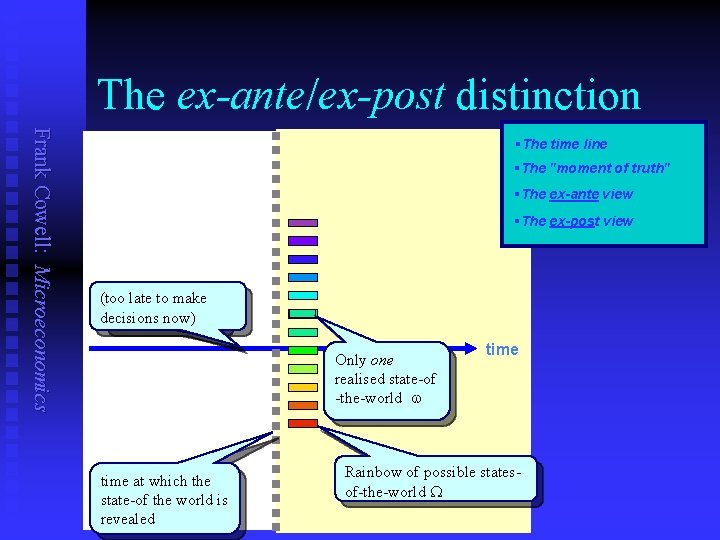
The ex-ante/ex-post distinction Frank Cowell: Microeconomics §The time line §The "moment of truth" §The ex-ante view §The ex-post view (too Decisions late to make to be decisions made here now) Only one realised state-of -the-world w time at which the state-of the world is revealed time Rainbow of possible statesof-the-world W

A simplified approach. . . Frank Cowell: Microeconomics n n n Assume the state-space is finite-dimensional Then a simple diagrammatic approach can be used This can be made even easier if we suppose that payoffs are scalars u n A special example: u u n Consumption in state w is just xw (a real number) Take the case where #states=2 W = { RED, BLUE} The resulting diagram may look familiar. . .

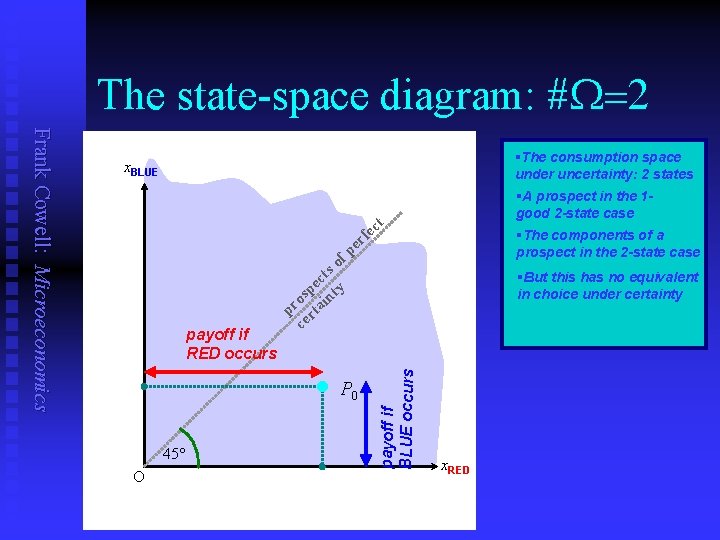
The state-space diagram: #W=2 §A prospect in the 1 good 2 -state case t c fe payoff if RED occurs of s ct e sp inty o pr rta ce · 45° O §The components of a prospect in the 2 -state case r pe P 0 §But this has no equivalent in choice under certainty payoff if BLUE occurs Frank Cowell: Microeconomics §The consumption space under uncertainty: 2 states x. BLUE x. RED

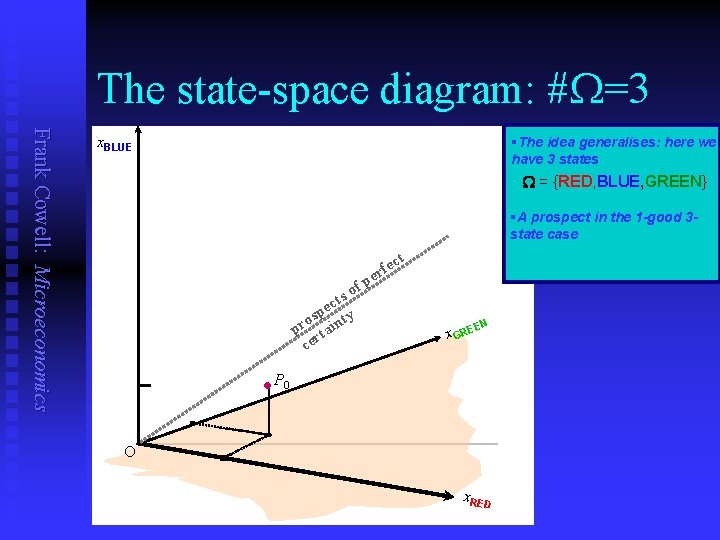
The state-space diagram: #W=3 Frank Cowell: Microeconomics x. BLUE §The idea generalises: here we have 3 states W = {RED, BLUE, GREEN} §A prospect in the 1 -good 3 state case ct e f er fp o cts e osp inty r p rta ce • P EN x GRE 0 O x. RED

The modified commodity space Frank Cowell: Microeconomics n n n We could treat the states-of-the-world like characteristics of goods. We need to enlarge the commodity space appropriately. Example: u The set of physical goods is {apple, banana, cherry}. u Set of states-of-the-world is {rain, sunshine}. u We get 3 x 2 = 6 “state-specific” goods. . . u. . . {a-r, a-s, b-r, b-s, c-r, c-s}. Can the invoke standard axioms over enlarged commodity space. But is more involved…?

Overview. . . Frank Cowell: Microeconomics Consumption: Uncertainty Modelling uncertainty Extending the standard consumer axioms Preferences Expected utility The felicity function

What about preferences? Frank Cowell: Microeconomics n n We have enlarged the commodity space. It now consists of “state-specific” goods: u u u n n n For finite-dimensional state space it’s easy. If there are #W possible states then. . . instead of n goods we have n #W goods. Some consumer theory carries over automatically. Appropriate to apply standard preference axioms. But they may require fresh interpretation. A little revision

Another look at preference axioms Frank Cowell: Microeconomics Completeness n Transitivity n Continuity n Greed n (Strict) Quasi-concavity n Smoothness n to ensure existence of indifference curves to give shape of indifference curves

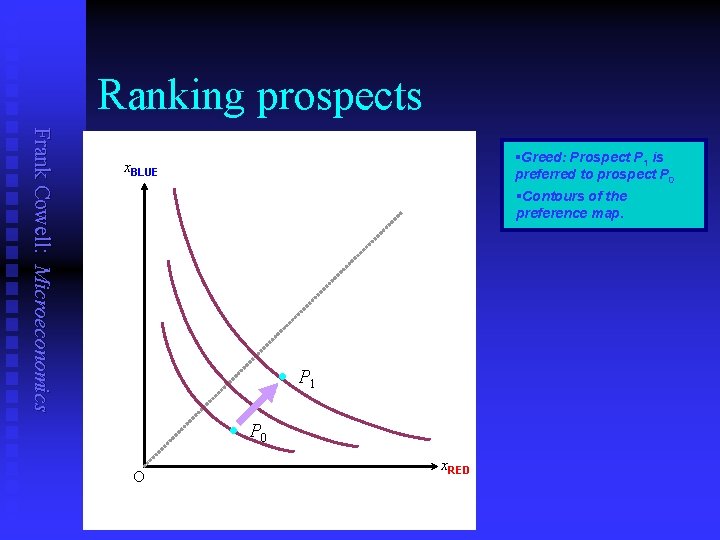
Ranking prospects Frank Cowell: Microeconomics §Greed: Prospect P 1 is preferred to prospect P 0 x. BLUE §Contours of the preference map. · P 1 · P 0 O x. RED

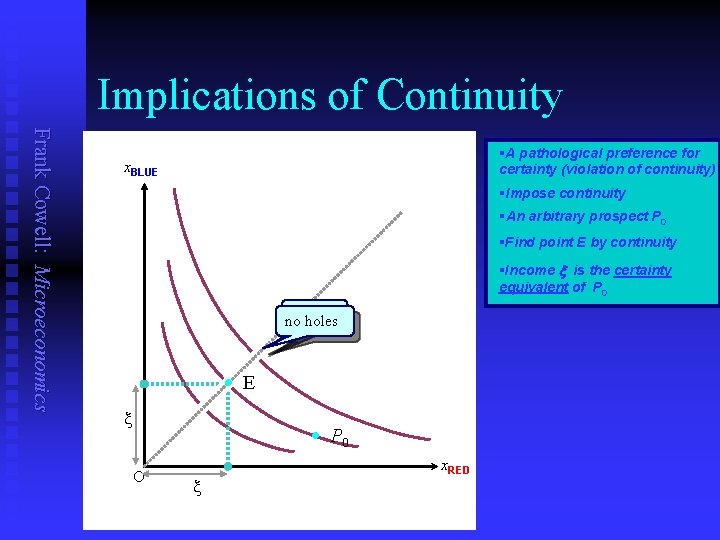
Implications of Continuity Frank Cowell: Microeconomics §A pathological preference for certainty (violation of continuity) x. BLUE §Impose continuity §An arbitrary prospect P 0 §Find point E by continuity §Income x is the certainty equivalent of P 0 holes no holes · E x · P 0 O x x. RED

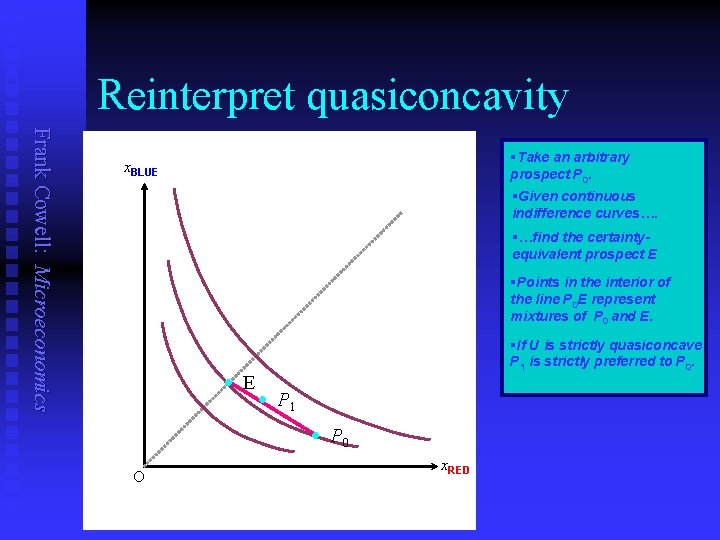
Reinterpret quasiconcavity Frank Cowell: Microeconomics §Take an arbitrary prospect P 0. x. BLUE §Given continuous indifference curves…. §…find the certaintyequivalent prospect E §Points in the interior of the line P 0 E represent mixtures of P 0 and E. · E §If U is strictly quasiconcave P 1 is strictly preferred to P 0. · P 1 · P 0 O x. RED

More on preferences? Frank Cowell: Microeconomics We can easily interpret the standard axioms. n But what determines the shape of the indifference map? n n Two main points: u Perceptions of the riskiness of the outcomes in any prospect u Aversion to risk pursue the first of these. . .

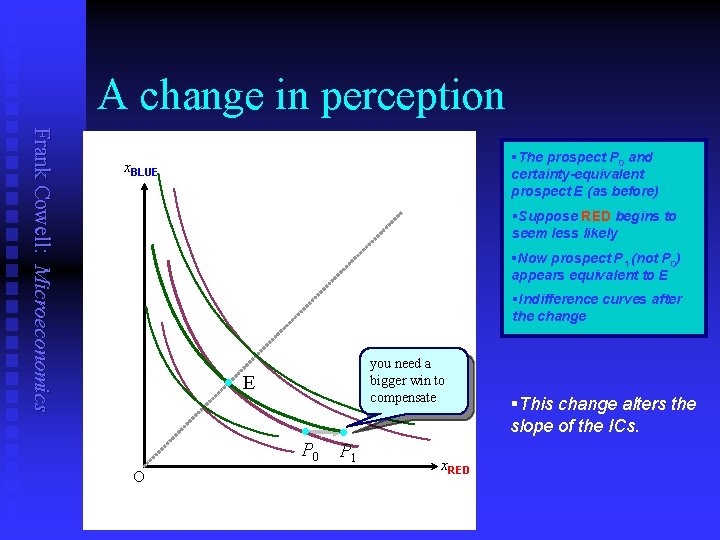
A change in perception Frank Cowell: Microeconomics §The prospect P 0 and certainty-equivalent prospect E (as before) x. BLUE §Suppose RED begins to seem less likely §Now prospect P 1 (not P 0) appears equivalent to E §Indifference curves after the change you need a bigger win to compensate · E · ·. P 0 P 1. O x. RED §This change alters the slope of the ICs.

A provisional summary Frank Cowell: Microeconomics n n n In modelling uncertainty we can: . . . distinguish goods by state-of-the-world as well as by physical characteristics etc. . extend consumer axioms to this classification of goods. . from indifference curves get the concept of “certainty equivalent”. . model changes in perceptions of uncertainty about future prospects. But can we do more?

Overview. . . Frank Cowell: Microeconomics Consumption: Uncertainty Modelling uncertainty The foundation of a standard representation of utility Preferences Expected utility The felicity function

A way forward Frank Cowell: Microeconomics n n For more results we need more structure on the problem. Further restrictions on the structure of utility functions. We do this by introducing extra axioms. Three more to clarify the consumer's attitude to uncertain prospects. u u By the way, there's a certain that’s been carefully avoided so far. Can you think what it might be. . . ?

Three key axioms. . . Frank Cowell: Microeconomics n State irrelevance: u n Independence: u n The identity of the states is unimportant Induces an additively separable structure Revealed likelihood: u Induces a coherent set of weights on states-ofthe-world A closer look

1: State irrelevance Frank Cowell: Microeconomics n Whichever state is realised has no intrinsic value to the person n There is no pleasure or displeasure derived from the state-of-the-world per se. Relabelling the states-of-the-world does not affect utility. All that matters is the payoff in each state-of-theworld. n n

2: The independence axiom Frank Cowell: Microeconomics n n n Let P(z) and P′(z) be any two distinct prospects such that the payoff in state-of-the-world is z. u x = x ′ = z. If U(P(z)) ≥ U(P′(z)) for some z then U(P(z)) ≥ U(P′(z)) for all z One and only one state-of-the-world can occur. So, assume that the payoff in one state is fixed for all prospects. The level at which the payoff is fixed should have no bearing on the orderings over prospects whose payoffs can differ in other states of the world. We can see this by partitioning the state space for #W > 2

Independence axiom: illustration Frank Cowell: Microeconomics x. BLUE §A case with 3 states-of-theworld § Compare prospects with the same payoff under GREEN. §Ordering of these prospects should not depend on the size of the payoff under GREEN. What if we compare all of these points. . . ? Or all of these points. . . ? EN x GRE Or all of these? O x. RED

3: The “revealed likelihood” axiom Frank Cowell: Microeconomics n n n Let x and x′ be two payoffs such that x is weakly preferred to x′. Let W 0 and W 1 be any two subsets of W. Define two prospects: u P 0 : = {x′ if w W 0 and x if w W 0} u P 1 : = {x′ if w W 1 and x if w W 1} If U(P 1 )≥U(P 0 ) for some such x and x′ then U(P 1 )≥U(P 0 ) for all such x and x′ Induces a consistent pattern over subsets of states-of-theworld.

Revealed likelihood: example Frank Cowell: Microeconomics §Assume these preferences over fruit §Consider these two prospects §Choose a prospect: P 1 or P 2? 1 apple < 1 banana 1 cherry < 1 date States of the world §Another two prospects §Is your choice between P 3 and P 4 the same as between P 1 and P 2? (remember only one colour will occur) P 1: apple P 2: banana P 3 : P 4 : apple banana apple cherry cherry date date cherry banana apple

A key result Frank Cowell: Microeconomics n n n We now have a result that is of central importance to the analysis of uncertainty. Introducing the three new axioms: u State irrelevance u Independence u Revealed likelihood. . . implies that preferences must be representable in the form of a von Neumann-Morgenstern utility function: å pw u(xw) w W Properties of p and u in a moment. Consider the interpretation

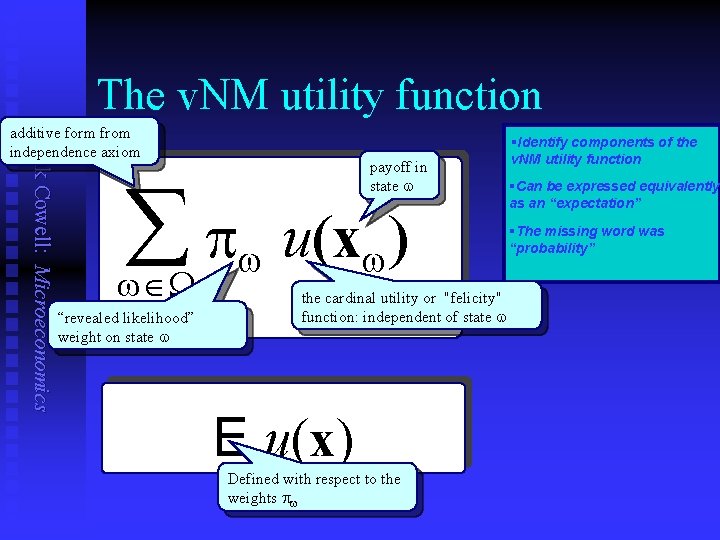
The v. NM utility function Frank Cowell: Microeconomics additive form from independence axiom payoff in state w å pw u(xw) w W “revealed likelihood” weight on state w the cardinal utility or "felicity" function: independent of state w E u(x) Defined with respect to the weights pw §Identify components of the v. NM utility function §Can be expressed equivalently as an “expectation” §The missing word was “probability”

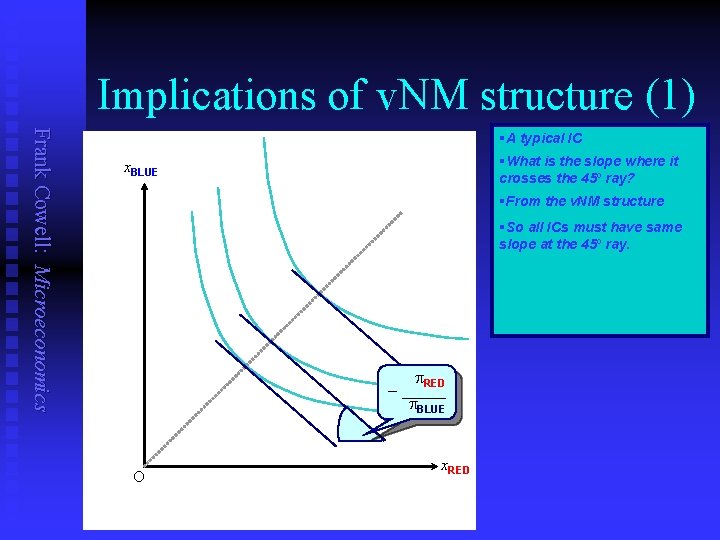
Implications of v. NM structure (1) Frank Cowell: Microeconomics §A typical IC §What is the slope where it crosses the 45º ray? x. BLUE §From the v. NM structure §So all ICs must have same slope at the 45º ray. p. RED – _____ p. BLUE O x. RED

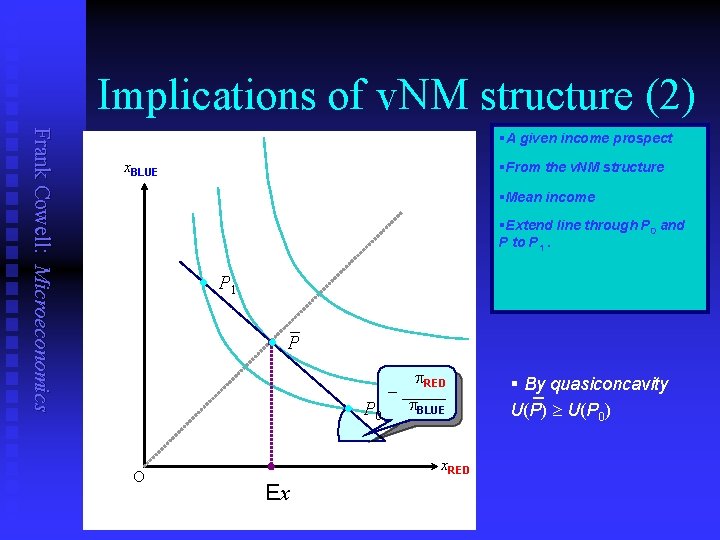
Implications of v. NM structure (2) Frank Cowell: Microeconomics §A given income prospect x. BLUE §From the v. NM structure §Mean income §Extend line through P 0 and P to P 1. · P 1 – · P 0 O p. RED – _____ p. BLUE x. RED Ex § By _ quasiconcavity U(P) U(P 0)

The v. NM paradigm: Summary Frank Cowell: Microeconomics n n n To make choice under uncertainty manageable it is helpful to impose more structure on the utility function. We have introduced three extra axioms. This leads to the von-Neumann-Morgenstern structure (there are other ways of axiomatising v. NM). This structure means utility can be seen as a weighted sum of “felicity” (cardinal utility). The weights can be taken as subjective probabilities. Imposes structure on the shape of the indifference curves.

Overview. . . Frank Cowell: Microeconomics Consumption: Uncertainty Modelling uncertainty A concept of “cardinal utility”? Preferences Expected utility The felicity function

The function u Frank Cowell: Microeconomics n The “felicity function” u is central to the v. NM structure. u u n Scale and origin of u are irrelevant: u u n n It’s an awkward name. But perhaps slightly clearer than the alternative, “cardinal utility function”. Check this by multiplying u by any positive constant… … and then add any constant. But shape of u is important. Illustrate this in the case where payoff is a scalar.

Risk aversion and concavity of u Frank Cowell: Microeconomics n Use the interpretation of risk aversion as quasiconcavity. n n If individual is risk averse. . . _. . . then U(P) U(P 0). n Given the v. NM structure. . . n n u(Ex) p. REDu(x. RED) + p. BLUEu(x. BLUE) u(p. REDx. RED+p. BLUEx. BLUE) p. REDu(x. RED) + p. BLUEu(x. BLUE) n So the function u is concave.

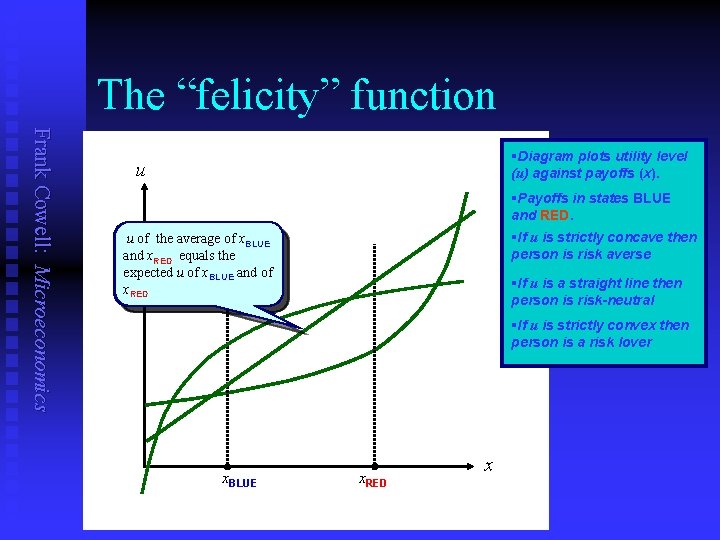
The “felicity” function Frank Cowell: Microeconomics §Diagram plots utility level (u) against payoffs (x). u §Payoffs in states BLUE and RED. §If u is strictly concave then person is risk averse u of the average of x. BLUE equals than the and x. RED higher expected u of x. BLUE and of x. RED §If u is a straight line then person is risk-neutral §If u is strictly convex then person is a risk lover x. BLUE x. RED x

Summary: basic concepts Frank Cowell: Microeconomics Review n u Review Use an extension of standard consumer theory to model uncertainty “state-space” approach Can reinterpret the basic axioms. n Need extra axioms to make further progress. n u n Yields the v. NM form. The felicity function gives us insight on risk aversion.

What next? Frank Cowell: Microeconomics Introduce a probability model. n Formalise the concept of risk. n This is handled in Risk. n