Prerequisites Almost essential Risk Frank Cowell Microeconomics November

Prerequisites Almost essential Risk Frank Cowell: Microeconomics November 2006 Risk Taking MICROECONOMICS Principles and Analysis Frank Cowell

Economics of risk taking Frank Cowell: Microeconomics n In the presentation Risk we examined the meaning of risk comparisons u u n n in terms of individual utility related to people’s wealth or income (ARA, RRA). In this presentation we put to this concept to work. We examine: u u u Trade under uncertainty A model of asset-holding The basis of insurance

Overview. . . Risk Taking Frank Cowell: Microeconomics Trade and equilibrium Extending the exchange economy Individual optimisation The portfolio problem

Trade Frank Cowell: Microeconomics n n Consider trade in contingent goods Requires contracts to be written ex ante. In principle we can just extend standard GE model. Use prices piw : u n n price of good i to be delivered in state w. We need to impose restrictions of v. NM utility. An example: u u Two persons, with differing subjective probabilities Two states-of the world Alf has all endowment in state BLUE Bill has all endowment in state RED

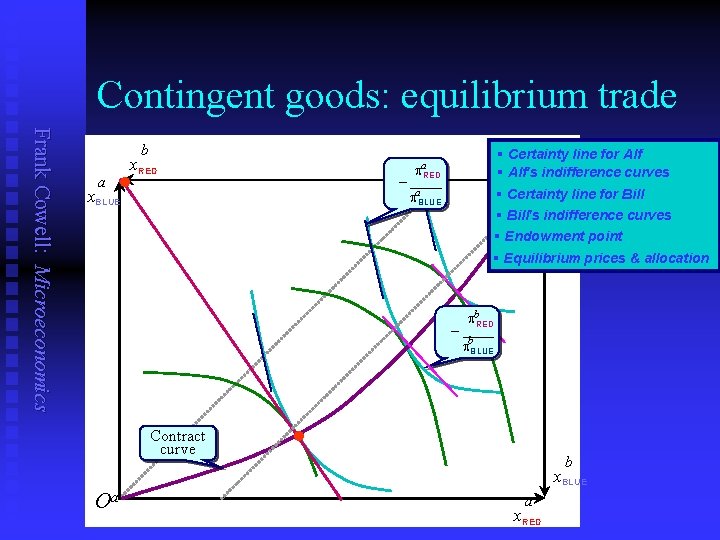
Contingent goods: equilibrium trade Frank Cowell: Microeconomics b a x. RED • § Certainty line for Alf § Alf's indifference curves Ob pa RED – ____ pa. BLUE x. BLUE § Certainty line for Bill § Bill's indifference curves § Endowment point § Equilibrium prices & allocation pb. RED – ____ pb. BLUE Contract curve • b x. BLUE Oa a x. RED

Trade: problems Frank Cowell: Microeconomics n Do all these markets exist? u u u n n Consider introduction of financial assets. Take a particularly simple form of asset: u u n If there are states-of-the-world. . . there are n of contingent goods. Could be a huge number a “contingent security” pays $1 if state w occurs. Can we use this to simplify the problem?

Financial markets? Frank Cowell: Microeconomics n n n The market for financial assets opens in the morning. Then the goods market is in the afternoon. We can use standard results to establish that there is a competitive equilibrium. Instead of n markets we now have n+. But there is an informational difficulty u u u To do your financial shopping you need information about the afternoon This means knowing the prices that there would be in each possible state of the world Has the scale of the problem really been reduced?

Overview. . . Risk Taking Frank Cowell: Microeconomics Trade and equilibrium Modelling the demand for financial assets Individual optimisation The portfolio problem

Individual optimisation Frank Cowell: Microeconomics n n n A convenient way of breaking down the problem A model of financial assets Crucial feature #1: the timing u u n Crucial feature #2: nature of initial wealth u u n Financial shopping done in the “morning” This determines wealth once state w is realised. Goods shopping done in the “afternoon. ” We will focus on the “morning”. Is it risk-free? Is it stochastic? Examine both cases

Interpretation 1: portfolio problem Frank Cowell: Microeconomics n n You have a determinate (non-random) endowment y You can keep it in one of two forms: u u n If there are just two possible states-of-the-world: u u n Money – perfectly riskless Bonds – have rate of return r: you could gain or lose on each bond. rº < 0 – corresponds to state BLUE r' > 0 – corresponds to state RED Consider attainable set if you buy an amount b of bonds where 0 ≤ b ≤ y

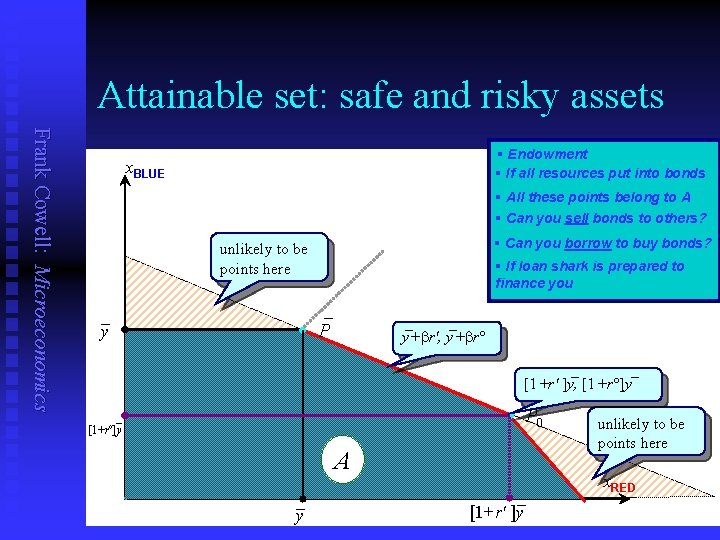
Attainable set: safe and risky assets Frank Cowell: Microeconomics § Endowment § If all resources put into bonds x. BLUE § All these points belong to A § Can you sell bonds to others? § Can you borrow to buy bonds? unlikely to be points here _ y § If loan shark is prepared to finance you _ _ _ y+br′, y+br · P _ _ [1+r′ ]y, [1+r ]y · P 0 _ [1+rº]y A _ y _ [1+r' ]y unlikely to be points here x. RED

Interpretation 2: insurance problem Frank Cowell: Microeconomics n You are endowed with a risky prospect Value of wealth ex-ante is y 0. u There is a risk of loss L. u If loss occurs then wealth is y 0 – L. u n You can purchase insurance against this risk of loss Cost of insurance is k. u In both states of the world ex-post wealth is y 0 – k. u n Use the same type of diagram.

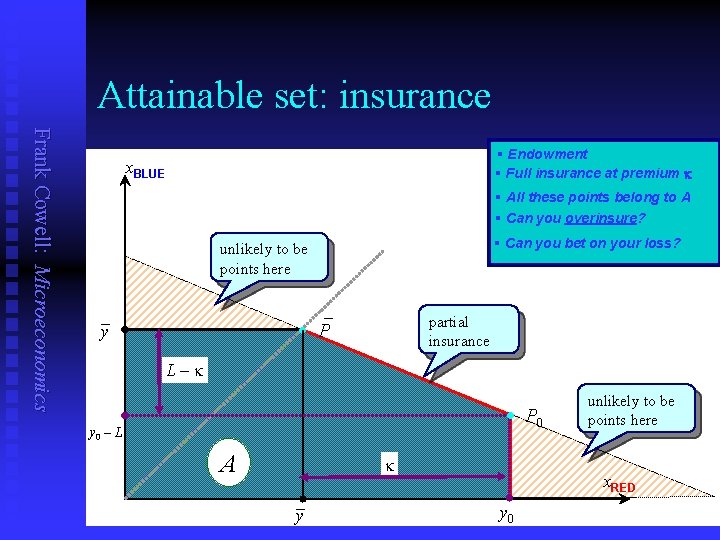
Attainable set: insurance Frank Cowell: Microeconomics § Endowment § Full insurance at premium k x. BLUE § All these points belong to A § Can you overinsure? § Can you bet on your loss? unlikely to be points here _ _ y partial insurance · P L–k · P 0 y 0 – L A k _ y unlikely to be points here x. RED y 0

A more general model? Frank Cowell: Microeconomics We have considered only two assets n Take the case where there are m assets (“bonds”) n Bond j has a rate of return rj, n Stochastic, but with known distribution. n Individual purchases an amount bj, n

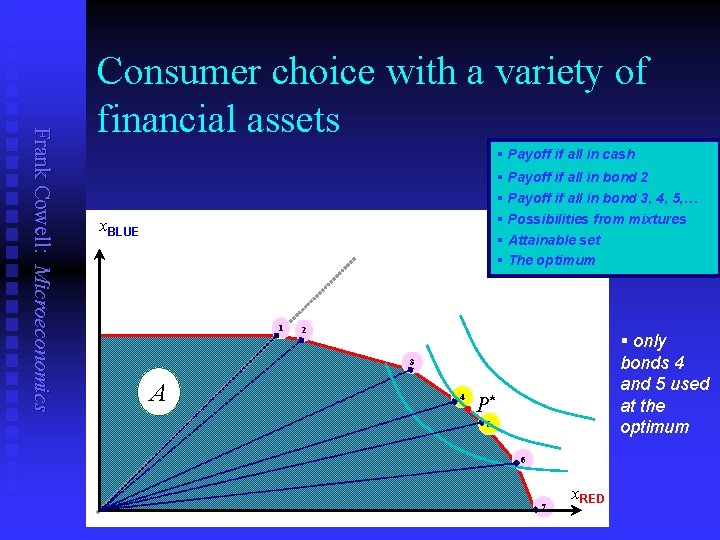
Frank Cowell: Microeconomics Consumer choice with a variety of financial assets § Payoff if all in cash § Payoff if all in bond 2 § Payoff if all in bond 3, 4, 5, … § Possibilities from mixtures § Attainable set § The optimum x. BLUE 1 2 § only bonds 4 and 5 used at the optimum 3 A 4 l P* 5 6 7 x. RED

Frank Cowell: Microeconomics Simplifying the financial asset problem n If there is a large number of financial assets many may be redundant. u u n n n which are redundant depends on tastes… … and on rates of return In the case of #W = 2, a maximum of two assets are used in the optimum. So the two-asset model of consumer optimum may be a useful parable. Let’s look a little closer.

Overview. . . Risk Taking Frank Cowell: Microeconomics Trade and equilibrium Safe and risky assets comparative statics Individual optimisation The portfolio problem

The portfolio problem Frank Cowell: Microeconomics n n We will look at the equilibrium of an individual risk-taker Makes a choice between a safe and a risky asset. u u n n “money” – safe, but return is 0 “bonds”– return r could be > 0 or < 0 Diagrammatic approach uses the two-state case But in principle could have an arbitrary distribution of r…

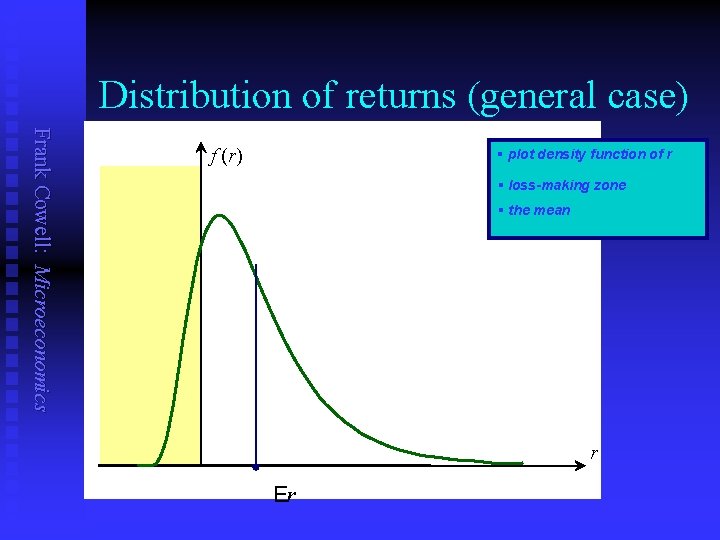
Distribution of returns (general case) Frank Cowell: Microeconomics f (r) § plot density function of r § loss-making zone § the mean r Er

Problem and its solution Frank Cowell: Microeconomics n n Agent has a given initial wealth y. If he purchases an amount b of bonds: u u Final wealth then is y = y – b + b[1+r] This becomes y = y + br, a random variable n The agent chooses b to maximise Eu(y + br) n FOC is E(ruy(y + b*r)) = 0 for an interior solution u u n where uy( • ) = u( • ) / y b* is the utility-maximising value of b. But corner solutions may also make sense. . .

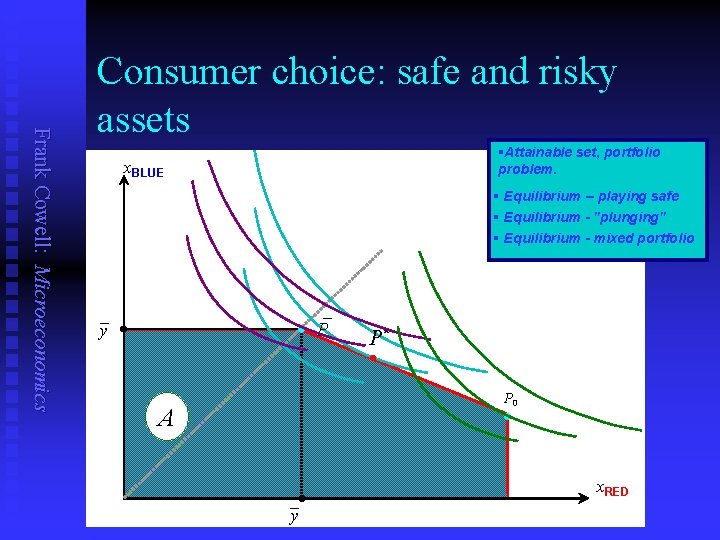
Frank Cowell: Microeconomics Consumer choice: safe and risky assets §Attainable set, portfolio problem. x. BLUE § Equilibrium -- playing safe § Equilibrium - "plunging" § Equilibrium - mixed portfolio _ _ y · P P* l P 0 · A _ y x. RED

Results (1) Frank Cowell: Microeconomics n n n Will the agent take a risk? Can we rule out playing safe? Consider utility in the neighbourhood of b = 0 Eu(y + br) | ———— | = uy(y )Er b |b=0 uy is positive. So, if expected return on bonds is positive, agent will increase utility by moving away from b = 0.

Results (2) Frank Cowell: Microeconomics n Take the FOC for an interior solution. n Examine the effect on b* of changing a parameter. * For example differentiate E(ruy(y + b r)) = 0 w. r. t. y * 2 * * E(ruyy(y + b r)) + E(r uyy(y + b r)) b / y = 0 * * b – E(ruyy(y + b r)) —— = ———— * 2 y E(r uyy (y + b r)) n n Denominator is unambiguously negative n What of numerator?

Risk aversion and wealth Frank Cowell: Microeconomics n n n To resolve ambiguity we need more structure. Assume Decreasing ARA Theorem: If an individual has a v. NM utility function with DARA and holds a positive amount of the risky asset then the amount invested in the risky asset will increase as initial wealth increases

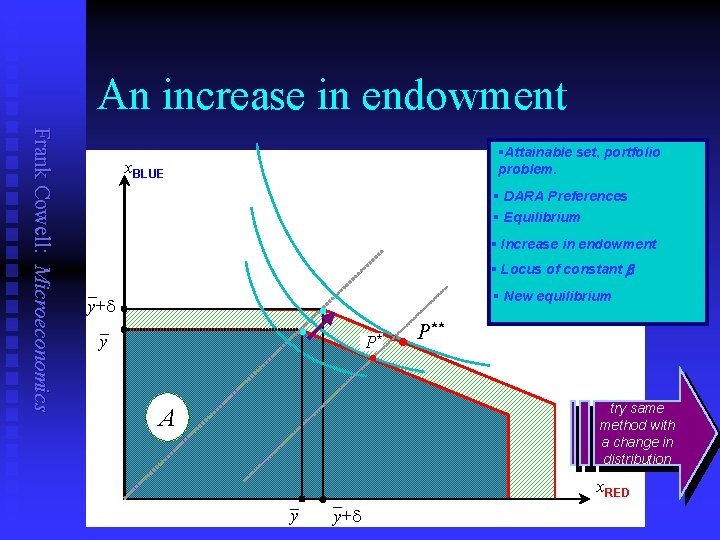
An increase in endowment Frank Cowell: Microeconomics §Attainable set, portfolio problem. x. BLUE § DARA Preferences § Equilibrium § Increase in endowment § Locus of constant b _ y+d _ y · § New equilibrium · P* o l P** l try same method with a change in distribution A _ y+d x. RED

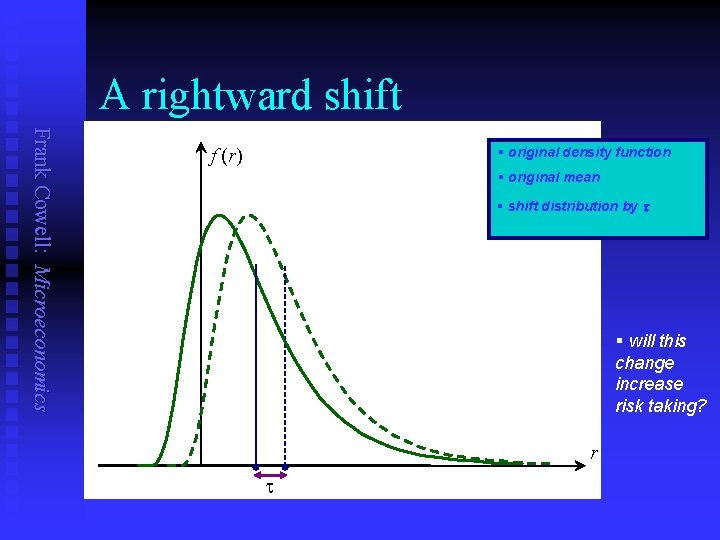
A rightward shift Frank Cowell: Microeconomics § original density function f (r) § original mean § shift distribution by t § will this change increase risk taking? r t

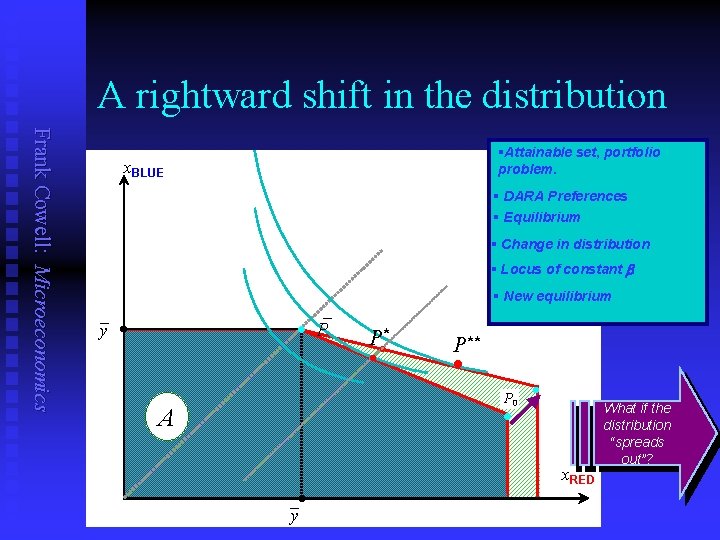
A rightward shift in the distribution Frank Cowell: Microeconomics §Attainable set, portfolio problem. x. BLUE § DARA Preferences § Equilibrium § Change in distribution § Locus of constant b § New equilibrium _ _ y · P Po* l P** l P 0 · · A x. RED _ y What if the distribution “spreads out”?

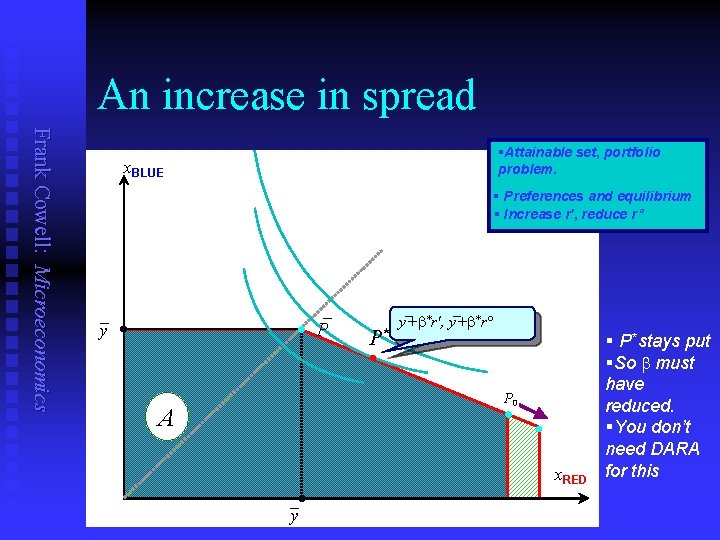
An increase in spread Frank Cowell: Microeconomics §Attainable set, portfolio problem. x. BLUE § Preferences and equilibrium § Increase r′, reduce r _ _ y · P P* _ _ y+b*r′, y+b*r l P 0 · A · x. RED _ y § P* stays put §So b must have reduced. §You don’t need DARA for this

Risk-taking results: summary Frank Cowell: Microeconomics n If the expected return to risk-taking is positive, then the individual takes a risk n If the distribution “spreads out” then risk taking reduces. n Given DARA, if wealth increases then risk-taking increases. n Given DARA, if the distribution “shifts right” then risk-taking increases.