Prerequisites Almost essential Contract Design Frank Cowell Microeconomics

Prerequisites Almost essential Contract Design Frank Cowell: Microeconomics September Design: Taxation MICROECONOMICS Principles and Analysis Frank Cowell

The design problem Frank Cowell: Microeconomics n n n The government needs to raise revenue… …and it may want to redistribute resources To do this it uses the tax system u u n Base it on “ability to pay” u u n income rather than wealth ability reflected in productivity Tax authority may have limited information u u n personal income tax… …and income-based subsidies who have the high ability to pay? what impact on individuals’ willingness to produce output? What’s the right way to construct the tax schedule?

A link with contract theory Frank Cowell: Microeconomics n Base approach on the analysis of contracts u u u n Ability here plays the role of unobservable type u u n close analogy with case of hidden characteristics owner hires manager… …but manager’s ability is unknown at time of hiring ability may not be directly observable… …but distribution of ability in the population is known A progressive treatment: u u outline model components use analogy with contracts to solve two-type case proceed to large (finite) number of types then extend to general continuous distribution

Overview. . . Design: Taxation Frank Cowell: Microeconomics Design basics Preferences, incomes, ability and the government Simple model Generalisations Interpretations

Model elements Frank Cowell: Microeconomics n A two-commodity model u u n Incomes only from work u u n individuals are paid according to their marginal product workers differ according to their ability Individuals derive utility from: u u n leisure (i. e. the opposite of effort) consumption – a basket of all other goods their leisure their disposable income (consumption) Government / tax agency u u u has to raise a fixed amount of revenue K seeks to maximise social welfare… …where social welfare is a function of individual utilities

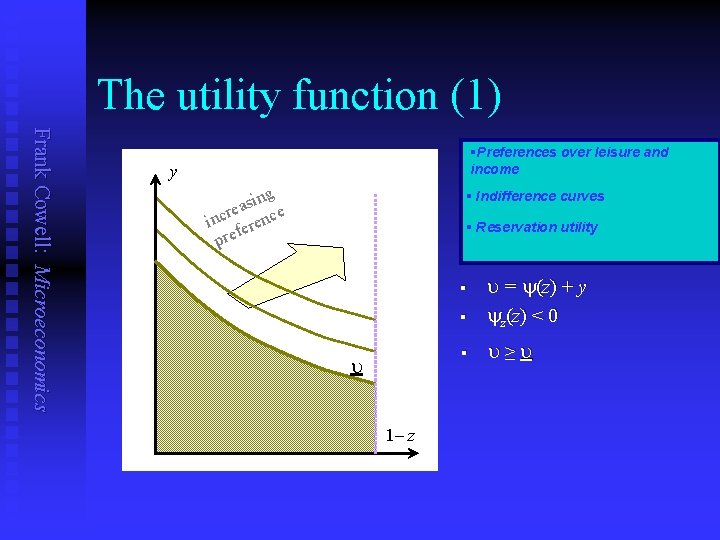
Modelling preferences Frank Cowell: Microeconomics n Individual’s preferences u u u n Special shape of utility function u u u n u = y(z) + y u : utility level z : effort y : income received y( ) : decreasing, strictly concave, function quasi-linear form zero-income effect y(z) gives the disutility of effort in monetary units Individual does not have to work u u reservation utility level u requires y(z) + y ≥ u

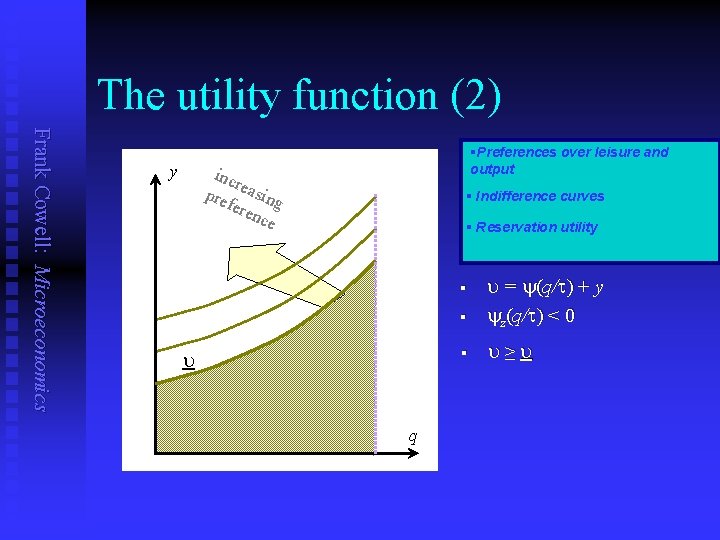
Ability and income Frank Cowell: Microeconomics n n Individuals work (give up leisure) to provide consumption Individuals differ in talent (ability) t u u n Disposable income determined by tax authority u u u n higher ability people produce more and may thus earn more individual of type t works an amount z produces output q = tz but individual does not necessarily get to keep this output? intervention via taxes and transfers fixes a relationship between individual’s output and income (net) income tax on type t is implicitly given by q − y Preferences can be expressed in terms of q and y u u for type t utility is given by y(z) + y equivalently: y(q / t) + y A closer look at utility

The utility function (1) Frank Cowell: Microeconomics §Preferences over leisure and income y sing a e r e inc erenc f pre § Indifference curves § Reservation utility § u = y(z) + y yz(z) < 0 § u≥u § u 1– z

The utility function (2) Frank Cowell: Microeconomics y §Preferences over leisure and output inc r pre easing fere nce § Indifference curves § Reservation utility § u = y(q/t) + y yz(q/t) < 0 § u≥u § u q

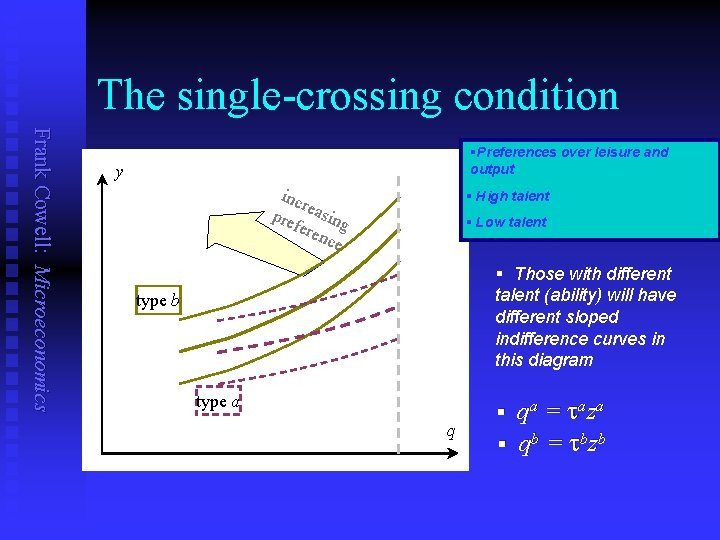
Indifference curves: pattern Frank Cowell: Microeconomics n n All types have the same preferences Function y( ) is common knowledge u u n but utility level u of type t depends on effort z and payment y value of t may be information that is private to individual Take indifference curves in (q, y) space u u = y(q/t) + y slope of a given type’s indifference curve depends on value of t indifference curves of different types cross once only

The single-crossing condition Frank Cowell: Microeconomics §Preferences over leisure and output y inc r pre easing fere nce § High talent § Low talent § Those with different talent (ability) will have different sloped indifference curves in this diagram type b type a q § § qa = taza qb = tbzb

Similarity with contract model Frank Cowell: Microeconomics n The position of the Agent u u n The position of the Principal (designer) u u u n instead of a single Agent with known ex-ante probability distribution of talents, … … a population of workers with known distribution of abilities. designer is the government acting as Principal. knows distribution of ability (common knowledge) the objective function is a standard SWF One extra constraint u u u the community has to raise a fixed amount K ≥ 0 the government imposes a tax drives a wedge between market income generated by worker and the amount available to spend on other goods.

Overview. . . Design: Taxation Frank Cowell: Microeconomics Design basics Analogy with contract theory Simple model Generalisations Interpretations

A full-information solution? Frank Cowell: Microeconomics n n Consider argument based on the analysis of contracts Given full information owner can fully exploit any manager u u n Same basic story here u u n Pays the minimum amount necessary “Chooses” their effort Can impose lump-sum tax “Chooses” agents’ effort — no distortion But the full-information solution may be unattractive u u u Informational requirements are demanding Perhaps violation of individuals’ privacy? So look at second-best case…

Two types Frank Cowell: Microeconomics n n Start with the case closest to the optimal contract model Exactly two skill types u u u n From contract design we can write down the outcome u n ta > tb proportion of a-types is p values of ta , tb and p are common knowledge essentially all we need to do is rework notation But let us examine the model in detail:

Second-best: two types Frank Cowell: Microeconomics n The government’s budget constraint u u n Participation constraint for the b type: u u n yb + y(zb) ≥ ub have to offer at least as much as available elsewhere Incentive-compatibility constraint for the a type: u u u n p[qa ya] + [1 p][qb yb ] ≥ K where qh yh is the amount raised in tax from agent h ya + y(qa/ta) ≥ yb + y(qb/ta) must be no worse off than if it behaved like a b-type implies (qb, yb) < (qa, ya) The government seeks to maximise standard SWF u u p z(y(za ) + ya ) + [1 p] z(y(zb ) + yb ) where z is increasing and concave

Two types: model Frank Cowell: Microeconomics n We can use a standard Lagrangean approach u u n Constraints are: u u u n government chooses (q, y) pairs for each type …subject to three constraints government budget constraint participation constraint (for b-types) incentive-compatibility constraint (for a-types) Choose qa , qb , ya , yb to max p z(y(qa/ta) + ya) + [1 p] z(y(qb/tb) + yb) + k [p[qa ya] + [1 p][qb yb ] K] + l [yb + y(qb/tb) ub] + m [ya + y(qa /ta ) yb y(qb /ta )] where k, l, m are Lagrange multipliers for the constraints

Two types: method Frank Cowell: Microeconomics n Differentiate with respect to qa, qb, ya, yb to get FOCs: u u n For an interior solution, where qa, qb, ya, yb are all positive u u n pzu (ua )yz (za )/ ta + kp + myz (za )/ ta ≤ 0 [1 p] zu (ub )yz (zb )/ tb + k [1 p] + lyz (zb )/ tb myz (qb/ ta )/ ta ≤ 0 pzu (ua ) kp + m ≤ 0 [1 p] zu (ub ) k[1 p] + l m ≤ 0 pzu(ua)yz(za)/ta + kp + myz(za)/ta = 0 [1 p]zu(ub)yz(zb)/tb + k [1 p] + lyz(zb)/tb myz(qb/ta)/ta = 0 pzu(ua) kp + m = 0 [1 p]zu(ub) k[1 p] + l m = 0 Manipulating these gives the main results u u u For example, from first and third condition: [kp m ] yz (za )/ta + kp + myz (za )/ta = 0 kp yz (za )/ta + kp = 0

Two types: solution Frank Cowell: Microeconomics n Solving the FOC we get: u u u n Also, all the Lagrange multipliers are positive u u n so the associated constraints are binding follows from standard adverse selection model Results are as for optimum-contracts model: u u n yz(qa/ta) = ta yz(qb/tb) = tb + kp/[1 p], where k : = yz(qb/tb) [tb/ta] yz(qb/ta) < 0 MRSa = MRTa MRSb < MRTb Interpretation u u u no distortion at the top (for type ta) no surplus at the bottom (for type tb) determine the “menu” of (q, y)-choices offered by tax agency….

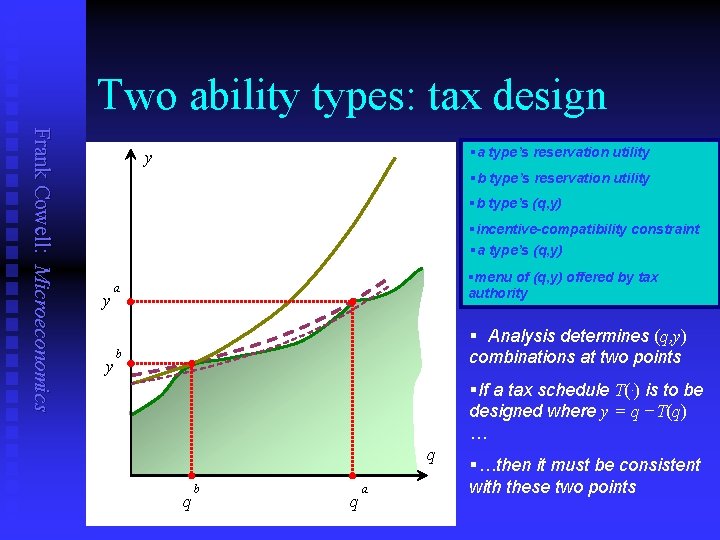
Two ability types: tax design Frank Cowell: Microeconomics §a type’s reservation utility y §b type’s reservation utility §b type’s (q, y) §incentive-compatibility constraint §a type’s (q, y) y §menu of (q, y) offered by tax authority a y § Analysis determines (q, y) combinations at two points b §If a tax schedule T(∙) is to be designed where y = q −T(q) … q q b q a §…then it must be consistent with these two points

Overview. . . Design: Taxation Frank Cowell: Microeconomics Design basics Moving beyond the two-ability model Simple model Generalisations Interpretations

A small generalisation Frank Cowell: Microeconomics n With three types problem becomes a bit more interesting u u u n We now have one more constraint to worry about 1. 2. 3. n Similar structure to previous case ta > tb > tc proportions of each type in the population are pa, pb, pc Participation constraint for c type: yc + y(qc/tc) ≥ uc IC constraint for b type: yb + y(qb/tb) ≥ yc + y(qc/tb) IC constraint for a type: ya + y(qa /ta ) ≥ yb + y(qb /ta ) But this is enough to complete the model specification u u the two IC constraints also imply ya + y(qa/ta) ≥ yc + y(qc/tb) … … so no-one has incentive to misrepresent as lower ability

Three types Frank Cowell: Microeconomics n Methodology is same as two-ability model u u u n Outcome essentially as before : u u u n n set up Lagrangean Lagrange multipliers for budget constraint, participation constraint and two IC constraints maximise with respect to (qa, ya), (qb, yb), (qc, yc) MRSa = MRTa MRSb < MRTb MRSc < MRTc Again, no distortion at the top and the participation constraint binding at the bottom u determines (q, y)-combinations at exactly three points u tax schedule must be consistent with these points A stepping stone to a much more interesting model…

A richer model: N+1 types Frank Cowell: Microeconomics n The multi-type case follows immediately from three types n Take N + l types u u n t 0 < t 1 < t 2 < … < t. N (note the required change in notation) proportion of type j is pj this distribution is common knowledge Budget constraint and SWF are now u u u Sj pj [qj yj ] ≥ K Sj pj z(y(zj) + yj) where sum is from 0 to N

N+1 types: behavioural constraints Frank Cowell: Microeconomics n Participation constraint u u u n Incentive-compatibility constraint u u u n is relevant for lowest type j = 0 form is as before: y 0 + y(z 0) ≥ u 0 applies where j > 0 j must be no worse off than if it behaved like the type below (j 1) yj + y(qj/tj) ≥ yj 1 + y(qj 1 /tj). implies (qj 1, yj 1) < (qj, yj) and u(tj) ≥ u(tj 1) From previous cases we know the methodology u (and can probably guess the outcome)

N+1 types: solution Frank Cowell: Microeconomics n n Lagrangean is only slightly modified from before Choose {(qj , yj )} to max Sj=0 pj z (y(qj / tj ) + yj ) + k [Sj pj [qj yj] K] + l [y 0 + y(z 0) u 0] + Sj=1 mj [yj + y(qj/tj) yj 1 y(qj 1 /tj)] where there are now N incentive-compatibility Lagrange multipliers n And we get the result, as before u u u n MRSN = MRTN MRSN− 1 < MRTN− 1 … MRS 1 < MRT 1 MRS 0 < MRT 0 Now the tax schedule is determined at N+1 points

A continuum of types Frank Cowell: Microeconomics n n One more step is required in generalisation Suppose the tax agency is faced with a continuum of taxpayers u u n This case can be reasoned from the case with N + 1 types u n allow N From previous cases we know u u u n common assumption allows for general specification of ability distribution form of the participation constraint form that IC constraint must take an outline of the outcome Can proceed by analogy with previous analysis…

The continuum model Frank Cowell: Microeconomics n Continuous ability u u n bounded support [t, `t ] density f(t) Utility for talent t as before u(t) = y(t) + y( q(t) / t) n Participation constraint is u(t) ≥ u n Incentive compatibility requires du(t) /dt ≥ 0 n SWF is `t ⌠ │ z (u(t)) f(t) dt ⌡t

Continuum model: optimisation Frank Cowell: Microeconomics n Lagrangean is `t ⌠ │ z (u(t)) f(t) dt ⌡t `t ⌠ + k │ [ q(t) − y(t) − K] f(t) dt ⌡t + l [ u(t) − u] `t ⌠ du(t) + │ m(t) —— f(t) dt ⌡t dt where u(t) = y(t) + y( q(t) / t) n Lagrange multipliers are u u u n k : government budget constraint l : participation constraint m(t) : incentive-compatibility for type t Maximise Lagrangean with respect to q(t) and y(t) for all t [t, `t ]

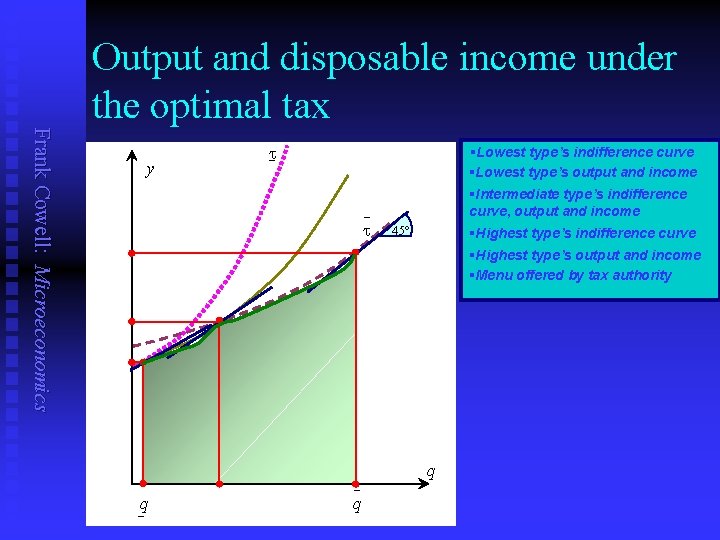
Output and disposable income under the optimal tax Frank Cowell: Microeconomics y t_ §Lowest type’s indifference curve §Lowest type’s output and income §Intermediate type’s indifference curve, output and income §Highest type’s indifference curve _ t 45° §Highest type’s output and income §Menu offered by tax authority _ _q q q

Continuum model: results Frank Cowell: Microeconomics n Incentive compatibility implies u u n No distortion at top implies u u n dy /dq > 0 optimal marginal tax rate < 100% dy /dq = 1 zero optimal marginal tax rate! But explicit form for the optimal income tax requires u u specification of distribution f(∙) specification of individual preferences y(∙) specification of social preferences z (∙) specification of required revenue K

Overview. . . Design: Taxation Frank Cowell: Microeconomics Design basics Applying design rules to practical policy Simple model Generalisations Interpretations

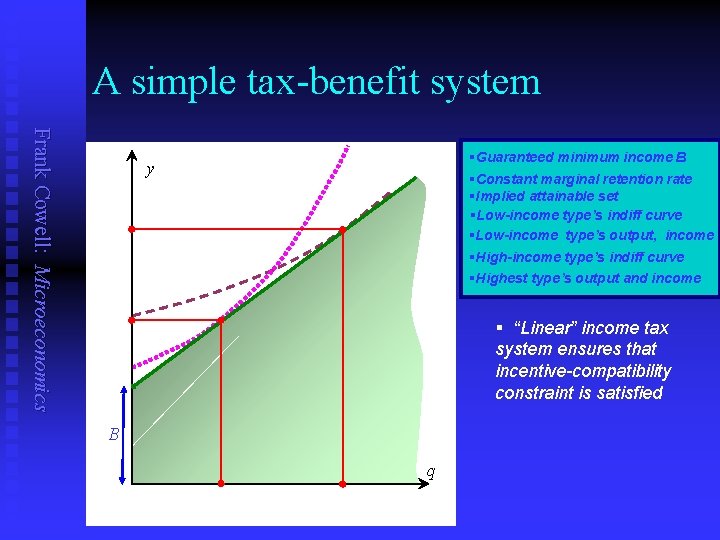
Application of design principles Frank Cowell: Microeconomics n The second-best method provides some pointers u u u n Simple schemes may be worth considering u u n roughly correspond to actual practice illustrate good/bad design Consider affine (linear) tax system u u u n but is not a prescriptive formula model is necessarily over-simplified exact second-best formula might be administratively complex benefit B payable to all (guaranteed minimum income) all gross income (output) taxable at the same marginal rate t… …constant marginal retention rate: dy /dq = 1 t Effectively a negative income tax scheme: u u (net) income related to output thus: y = B + [1 t] q so y > q if q < B / t … and vice versa

A simple tax-benefit system Frank Cowell: Microeconomics §Guaranteed minimum income B §Constant marginal retention rate §Implied attainable set §Low-income type’s indiff curve §Low-income type’s output, income y 1 t §High-income type’s indiff curve §Highest type’s output and income § “Linear” income tax system ensures that incentive-compatibility constraint is satisfied B q

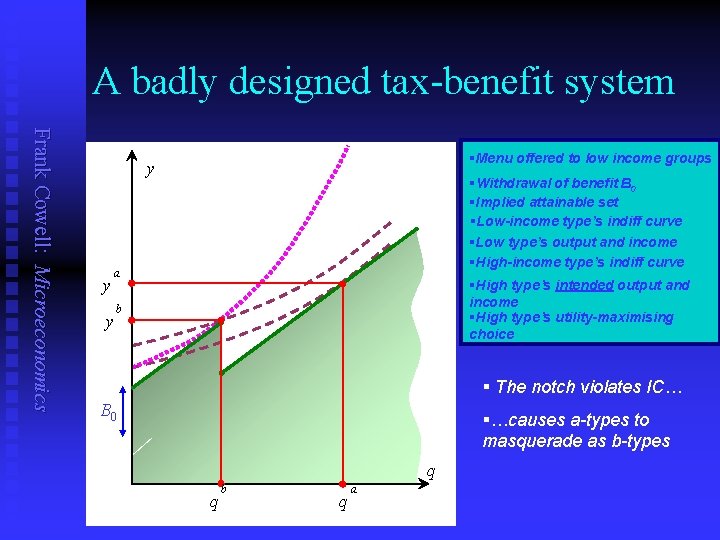
Violations of design principles? Frank Cowell: Microeconomics n n Sometimes the IC condition be violated in actual design This can happen by accident: u u u n Commonly known as u u n interaction between income support and income tax. generated by the desire to “target” support more effectively a well-meant inefficiency? the “notch problem” (US) the “poverty trap” (UK) Simple example u u u suppose some of the benefit is intended for lowest types only an amount B 0 is withdrawn after a given output level relationship between y and q no longer continuous and monotonic

A badly designed tax-benefit system Frank Cowell: Microeconomics §Menu offered to low income groups y y §Withdrawal of benefit B 0 §Implied attainable set §Low-income type’s indiff curve §Low type’s output and income §High-income type’s indiff curve a y §High type’s intended output and income §High type’s utility-maximising choice b § The notch violates IC… B 0 §…causes a-types to masquerade as b-types q q b q a

Summary Frank Cowell: Microeconomics n n n Optimal income tax is a standard second-best problem Elementary version a reworking of the contract model Can be extended to general ability distribution Provides simple rules of thumb for good design In practice these may be violated by well-meaning policies