Mathematical Analysis of Perturbed Orbits Special and General

Mathematical Analysis of Perturbed Orbits (Special and General Perturbations)

Perturbed Orbits Ø A perturbation is a deviation from some normal or expected motion. Ø In case of a satellite, the actual path will vary from theoretical two-body path due to perturbations caused by various forces and other bodies as well. Ø These perturbations have a significant impact, when studying the long term behavior of satellite orbits. Ø Major impact on interplanetary missions.

Special Perturbations Approach Ø Need to solve the relative equation of motion with perturbing forces. Ø Special perturbations methods generate just one special trajectory for a definite satellite, given its unique initial conditions. Ø A determination of the orbit is made by means of a numerical step-by-step process. (positions and velocities at later times by numerical integration) Ø Cowell’s method and Encke’s method.

Cowell’s Method Ø Simplest and most widely used method for the computation of perturbed satellite orbits. Ø The application of Cowell’s method is simply to write the equations of motion of object (of a two bodies problem), with the perturbations, and then to integrate them step-by-step numerically. Ø Thus we have a second order differential equation of a form

Cowell’s Method

Encke’s Method Ø In this method, the difference between the primary acceleration and all perturbing accelerations is integrated. Ø Encke’s method uses a reference two-body orbit whose initial position and velocity equal that of the orbit with perturbations. Ø Thus all the calculations and position, velocity would be with respect to the reference trajectory (Osculating orbit).

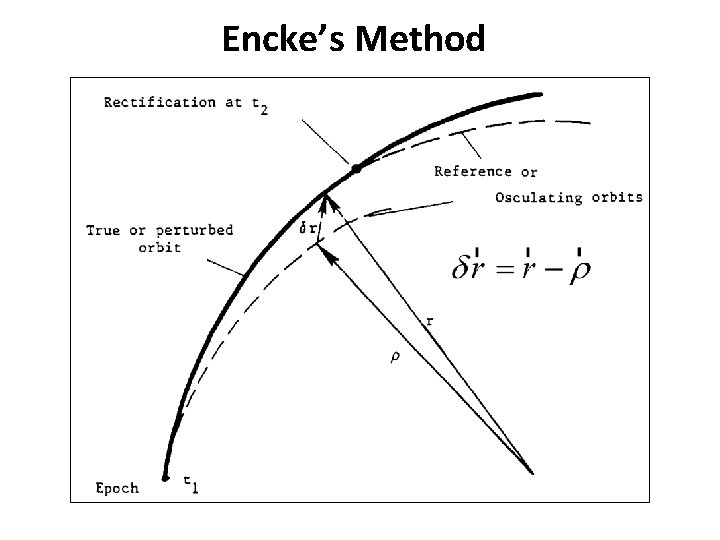
Encke’s Method

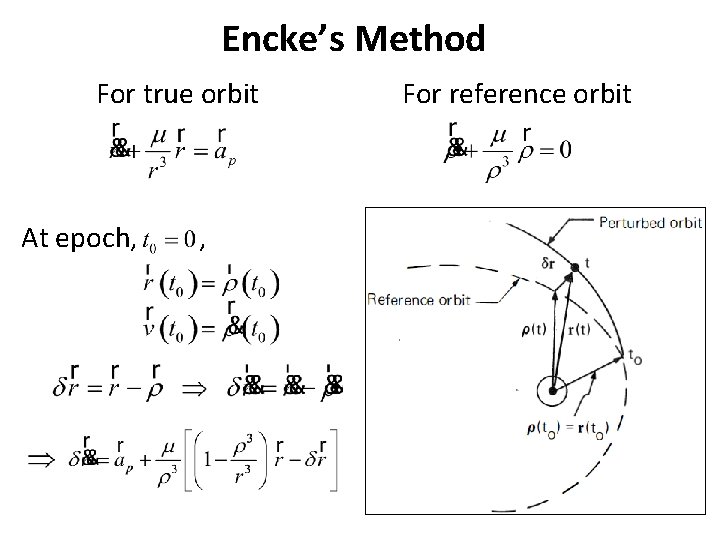
Encke’s Method For true orbit At epoch, , For reference orbit

Encke Manipulations A more attractive form: So finally,

Encke’s Method – Summary Ø At time = 0, Ø The actual orbit position and velocity vectors can be computed through Ø Orbit rectification For too large. A new reference orbit must be selected such that at the particular time of rectification ,

Cowell’s vs Encke’s method

Reference(s) (1) Roger R. Bate, Donald D. Mueller & Jerry E. White, Fundamentals of Astrodynamics, Dover Publications Inc. , New York, 1971. (2) Vladimir A. Chobotov, Orbital Mechanics, Third Edition, American Institute of Aeronautics and Astronautics Inc. , 2002. (3) John L. Junkins, “Integration of Perturbed Motion”, Teaching presentation notes, University at Buffalo, The State University of New York, 2006.