Prerequisites Almost essential Risk SIGNALLING MICROECONOMICS Principles and

Prerequisites Almost essential Risk SIGNALLING MICROECONOMICS Principles and Analysis Frank Cowell April 2018 Frank Cowell: Signalling 1

Introduction § A key aspect of hidden information § Information relates to personal characteristics • hidden information about actions is dealt with under “moral hazard” § But a fundamental difference from screening • informed party moves first • opposite case (where uninformed party moves first) dealt with under “adverse selection” § Nature of strategic problem • uncertainty about characteristics: game of imperfect information • updating by uninformed party in the light of the signal • equilibrium concept: perfect Bayesian Equilibrium (PBE) April 2018 Frank Cowell: Signalling 2

Signalling § Agent with the information makes first move: • subtly different from other “screening” problems • move involves making a signal § Types of signal • could be a costly action (physical investment, advertising, acquiring an educational certificate) • could be a costless message (manufacturers' assurances of quality, promises by service deliverers) § Message is about a characteristic • this characteristic cannot be costlessly observed by others • let us call it “talent” April 2018 Frank Cowell: Signalling 3

Talent § Suppose individuals differ in terms of hidden talent τ § Talent is valuable in the market • but possessor of τ cannot convince buyers in the market • without providing a signal that he has it § If a signal is not possible • may be no market equilibrium § If a signal is possible • will there be equilibrium? • more than one equilibrium? April 2018 Frank Cowell: Signalling 4

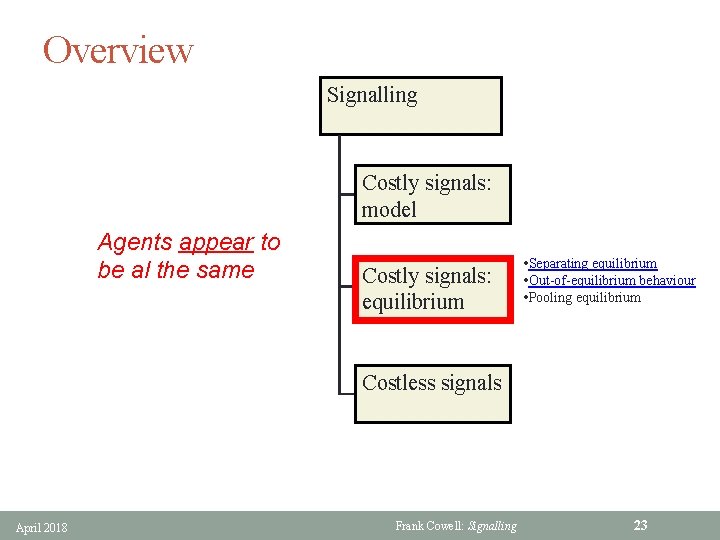
Overview Signalling Costly signals: model An educational analogy Costly signals: equilibrium Costless signals April 2018 Frank Cowell: Signalling 5

Costly signals § Suppose that a “signal” costs something • physical investment • forgone income § Consider a simple model of the labour market § Suppose productivity depends on ability • ability is not observable § Two types of workers: • the able – ta • the basic – tb • ta > tb § Single type of job • employers know the true product of a type t-person • if they can identify which is which § How can able workers distinguish themselves from others? April 2018 Frank Cowell: Signalling 6

Signals: educational “investment” § Consider the decision about whether acquire education § Suppose talent on the job identical to talent at achieving educational credentials • assumed to be common knowledge • may be worth “investing” in the acquisition of credentials § Education does not enhance productive ability • simply an informative message or credential • flags up innate talent • high ability people acquire education with less effort § Education is observable • certificates can be verified costlessly • firms may use workers'’ education as an informative signal April 2018 Frank Cowell: Signalling 7

Signalling by workers 0 p 1 p [LOW] [HIGH] h [NOT INVEST] § “Nature” determines worker’s type § Workers decide on education § Firms make wage offers § Workers decide whether to accept h [INVEST] [NOT INVEST] [INVEST] f 1 [low] [high] §simultaneous offers: Bertrand competition f 2 [low] [high] §investment involves time and money [low] [high] [accept 1] jec … … … Examine stages 1 -3 more closely ] t 2 [re cep April 2018 [ac t] h Frank Cowell: Signalling 8

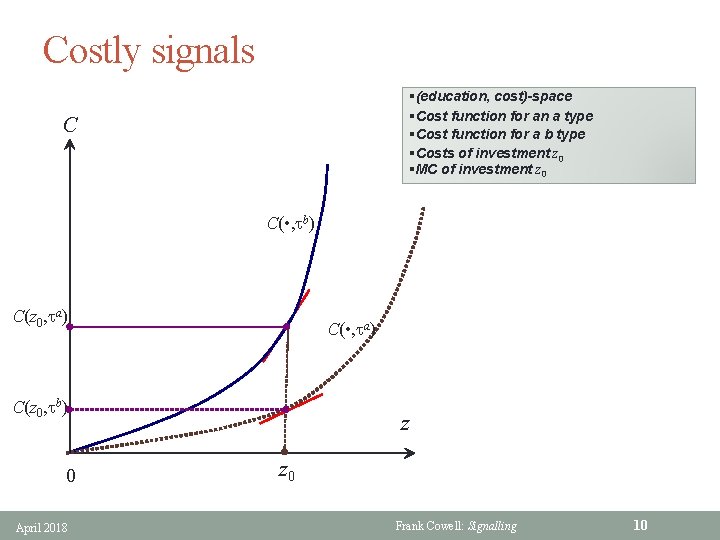
A model of costly signals § Previous sketch of problem is simplified • workers only make binary decisions (whether or not to invest) • firms only make binary decisions (high or low wage) § Suppose decision involve choices of z from a continuum § Ability is indexed by a person’s type t § Cost of acquiring education level z is C(z, t) ≥ 0 • C(0, t) = 0 Cz(z, t) > 0 • Czz(z, t) > 0 Czt(z, t) < 0 § Able person has lower cost for a given education level § Able person has lower MC for a given education level § Illustrate this for the two-type case April 2018 Frank Cowell: Signalling 9

Costly signals §(education, cost)-space §Cost function for an a type §Cost function for a b type §Costs of investment z 0 §MC of investment z 0 C C( • , tb) C(z 0, ta) C( • , ta) C(z 0, tb) 0 April 2018 z z 0 Frank Cowell: Signalling 10

Payoffs to individuals y 18 C(z, t) = (1/t) z 2 16 low t 14 12 § Talent does not enter the utility function directly 10 8 6 • individuals only care about income high t 4 z 2 • measure utility directly in terms of income: 0 0 • v(y, z; t) : = y C(z, t) 0. 5 1 1. 5 2 2. 5 • v depends on τ because talent reduces the cost of net income § Shape of C means that ICs in (z, y)-space satisfy single-crossing: • IC for a person with talent t is: y = u + C(z, t) • slope of IC for this type is: dy/dz = Cz(z, t) • for person with higher talent (t'>t) slope of IC is: dy/dz = Cz(z, t') • but Czt(z, t) < 0 so IC(t') is flatter than IC(t) at any value of z • so, if IC(t') and IC(t) intersect at (z 0, y 0) • IC(t') lies above original IC(t) for z < z 0 and below IC(t) for z > z 1 § This is important to simplify the structure of the problem Example April 2018 Frank Cowell: Signalling 11 3 3. 5

Rational behaviour § Workers: • assume income y is determined by wage § Wage is conditioned on “signal” that they provide • through acquisition of educational credentials § Type-τ worker chooses z to maximise • w(z) C(z, t) • where w(⋅) is wage schedule that workers anticipate will be offered by firms § Firms: • assume profits determined by workers’ talent § Need to design w(⋅) to max profits • depends on beliefs about distribution of talents • conditional on value of observed signal § What will equilibrium be? April 2018 Frank Cowell: Signalling 12

Overview Signalling Costly signals: model Costly signals discriminate among agents Costly signals: equilibrium • Separating equilibrium • Out-of-equilibrium behaviour • Pooling equilibrium Costless signals April 2018 Frank Cowell: Signalling 13

Separating equilibrium (1) § Start with a separating Perfect Bayesian Equilibrium § Both type-a and type-b agents are maximising • so neither wants to switch to using the other's signal § Therefore, for the talented a-types we have • f(ta) C(za, ta) ≥ f(tb) C(zb, ta) • if correctly identified, no worse than if misidentified as a b-type § Likewise for the b-types: • f(ta) C(za, tb) ≤ f(tb) C(zb, tb) § Rearranging this we have • C(za, tb) C(zb, tb) ≥ f(ta) f(tb) • positive because f(⋅) is strictly increasing and ta > tb • but since Cz > 0 this is true if and only if za > zb § So able individuals acquire more education than the others April 2018 Frank Cowell: Signalling 14

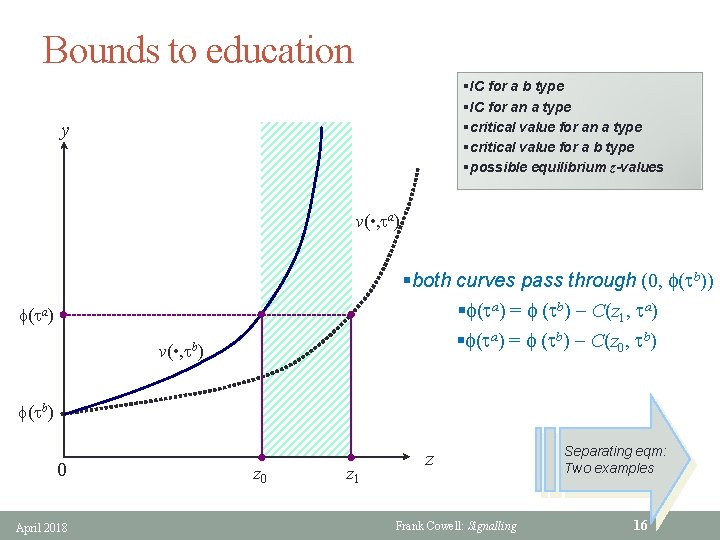
Separating equilibrium (2) § If there are just two types, at the optimum zb = 0 • everyone knows there are only two productivity types • education does not enhance productivity • so no gain to b-types in buying education § So, conditions for separating equilibrium become remember that • C(za, ta) ≤ f(ta) f(tb) C(0, t)=0 a b • C(z , t ) ≥ f(t ) § Let z 0, z 1 be the critical z-values that satisfy these conditions with equality • z 0 such that f(tb) = f(ta) C(z 0, tb) • z 1 such that f(tb) = f(ta) C(z 1, ta) § Values z 0, z 1 set limits to education in equilibrium April 2018 Frank Cowell: Signalling 15

Bounds to education §IC for a b type §IC for an a type §critical value for a b type §possible equilibrium z-values y v( • , ta) §both curves pass through (0, f(tb)) §f(ta) = f (tb) C(z 1, ta) §f(ta) = f (tb) C(z 0, tb) f(ta) v( • , tb) f(tb) 0 April 2018 z 0 z 1 z Frank Cowell: Signalling Separating eqm: Two examples 16

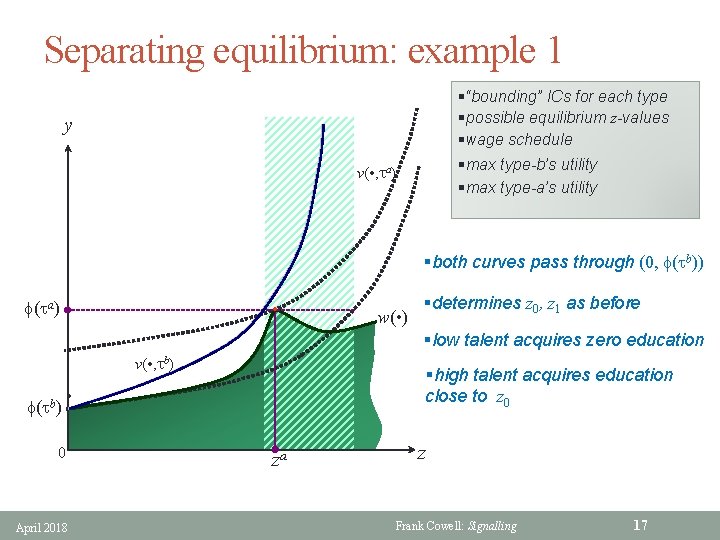
Separating equilibrium: example 1 §“bounding” ICs for each type §possible equilibrium z-values §wage schedule §max type-b’s utility §max type-a’s utility y v( • , ta) §both curves pass through (0, f(tb)) f(ta) • w( • ) §determines z 0, z 1 as before §low talent acquires zero education v( • , tb) f(tb) §high talent acquires education close to z 0 • 0 April 2018 za z Frank Cowell: Signalling 17

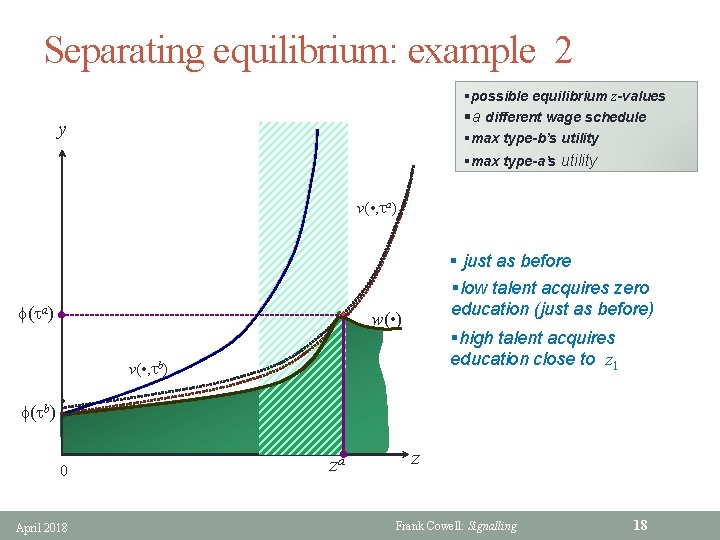
Separating equilibrium: example 2 §possible equilibrium z-values §a different wage schedule §max type-b’s utility y §max type-a’s utility v( • , ta) f(ta) • § just as before §low talent acquires zero education (just as before) w( • ) §high talent acquires education close to z 1 v( • , tb) f(tb) • 0 April 2018 za z Frank Cowell: Signalling 18

Overview Signalling Costly signals: model More on beliefs Costly signals: equilibrium • Separating equilibrium • Out-of-equilibrium behaviour • Pooling equilibrium Costless signals April 2018 Frank Cowell: Signalling 19

Out-of-equilibrium-beliefs: problem § For a given equilibrium can redraw w(⋅)-schedule • resulting attainable set for the workers must induce them to choose (za, f(ta)) and (0, f(tb)) § Shape of the w(⋅)-schedule at other values of z? • captures firms' beliefs about workers’ types in situations that do not show up in equilibrium § PBE leaves open what out-of-equilibrium beliefs may be April 2018 Frank Cowell: Signalling 20

Perfect Bayesian Equilibria § Requirements for PBE do not help us to select among the separating equilibria • try common sense? § Education level z 0 is the minimum-cost signal for a-types • a-type's payoff is strictly decreasing in za over [z 0, z 1] • any equilibrium with za > z 0 is dominated by equilibrium at z 0 § Are Pareto-dominated equilibria uninteresting? • important cases of strategic interaction that produce Pareto-dominated outcomes • need a proper argument, based on the reasonableness of such an equilibrium April 2018 Frank Cowell: Signalling 21

Out-of-equilibrium beliefs: a criterion § Is an equilibrium at za > z 0 “reasonable”? • requires w( • ) that sets w(z′) < f(ta) for z 0 < z′ < za • so firms must be assigning the belief π(z′) > 0 § Imagine someone observed choosing z′ • b-type IC through (z′, f(ta)) lies below the IC through (0, f(tb)) • a b-type knows he’s worse off than in the separating equilibrium • a b-type would never go to (z′, f(ta)) • so anyone at z′ out of equilibrium must be an a-type § An intuitive criterion: • π(z′) = 0 for any z′ (z 0, za) § So only separating equilibrium worth considering is where • a-types are at (z 0, f(ta)) • b-types are at (0, f(tb)) April 2018 Frank Cowell: Signalling 22

Overview Signalling Costly signals: model Agents appear to be al the same Costly signals: equilibrium • Separating equilibrium • Out-of-equilibrium behaviour • Pooling equilibrium Costless signals April 2018 Frank Cowell: Signalling 23

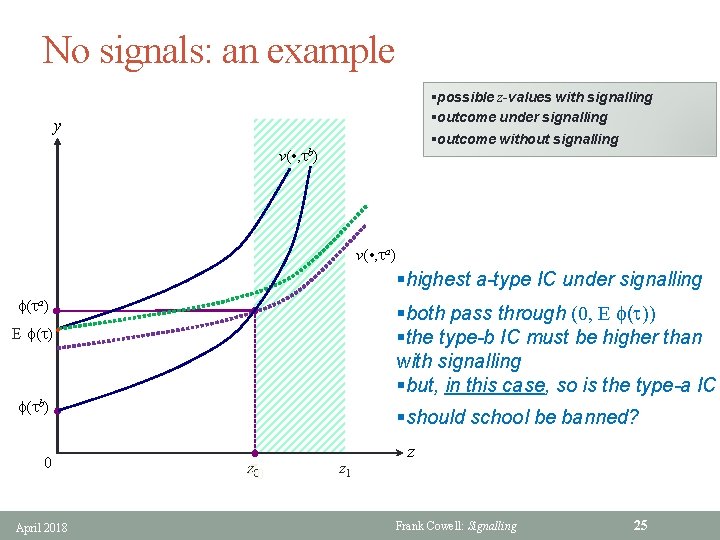
Pooling § There may be equilibria where the educational signal does not work • no-one finds it profitable to "invest" in education? • or all types purchase the same z? • depends on distribution of t • and relationship between marginal productivity and t § All workers present themselves with the same credentials • so they are indistinguishable • firms have no information to update their beliefs § Firms’ beliefs are derived from the distribution of t in the population • this distribution is common knowledge § So wage offered is expected marginal productivity Example • E f(t): =[1 p]f(ta) + pf(tb) § Being paid this wage might be in interests of all workers April 2018 Frank Cowell: Signalling 24

No signals: an example §possible z-values with signalling §outcome under signalling §outcome without signalling y v( • , tb) v( • , ta) §highest a-type IC under signalling f(ta) §both pass through (0, E f(t)) §the type-b IC must be higher than with signalling §but, in this case, so is the type-a IC E f(t) • f(tb) 0 April 2018 §should school be banned? zz 00 z 1 z Frank Cowell: Signalling 25

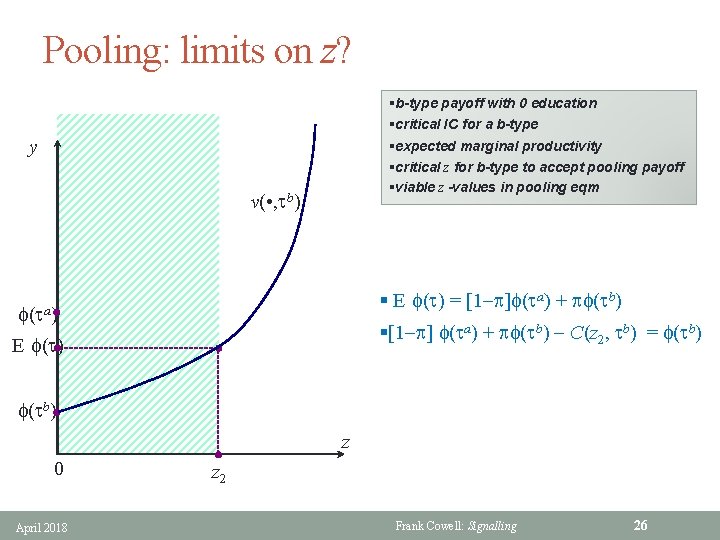
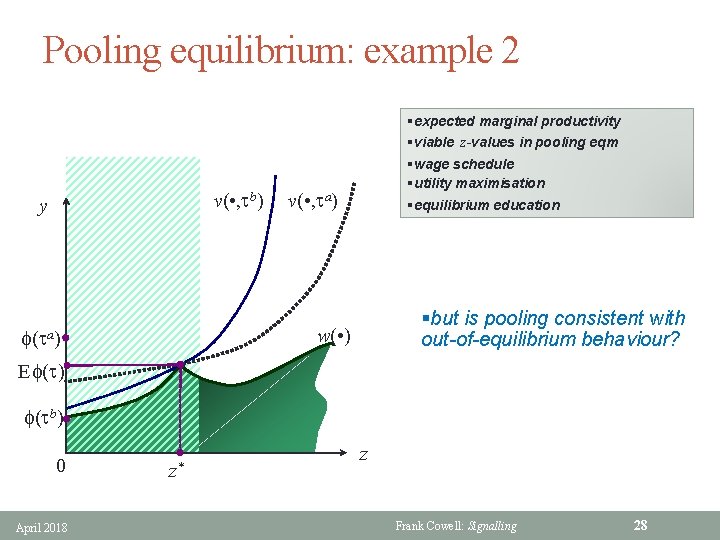
Pooling: limits on z? §b-type payoff with 0 education §critical IC for a b-type §expected marginal productivity §critical z for b-type to accept pooling payoff §viable z -values in pooling eqm y v( • , tb) § E f(t) = [1 p]f(ta) + pf(tb) f(ta) §[1 p] f(ta) + pf(tb) C(z 2, tb) = f(tb) E f(t) f(tb) z 0 April 2018 z 2 Frank Cowell: Signalling 26

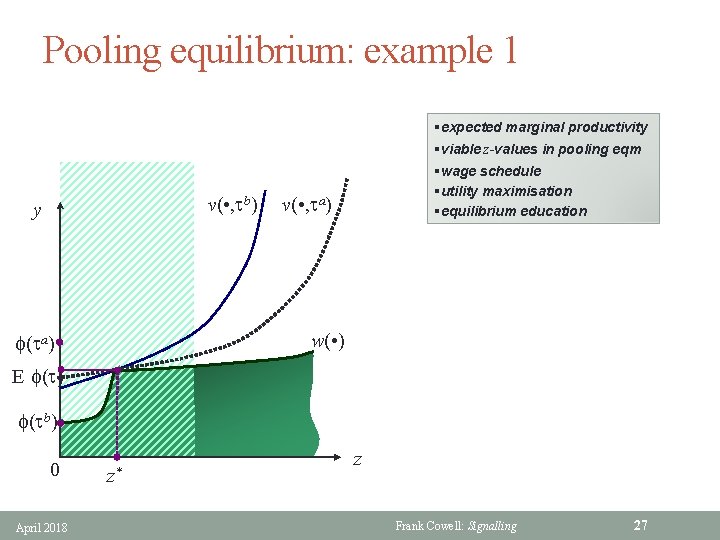
Pooling equilibrium: example 1 v( • , tb) y §expected marginal productivity §viable z-values in pooling eqm §wage schedule §utility maximisation §equilibrium education v( • , ta) w( • ) f(ta) E f(t) f(tb) 0 April 2018 z* z Frank Cowell: Signalling 27

Pooling equilibrium: example 2 v( • , tb) y §expected marginal productivity §viable z-values in pooling eqm §wage schedule §utility maximisation §equilibrium education v( • , ta) §but is pooling consistent with out-of-equilibrium behaviour? w( • ) f(ta) Ef(t) f(tb) 0 April 2018 z* z Frank Cowell: Signalling 28

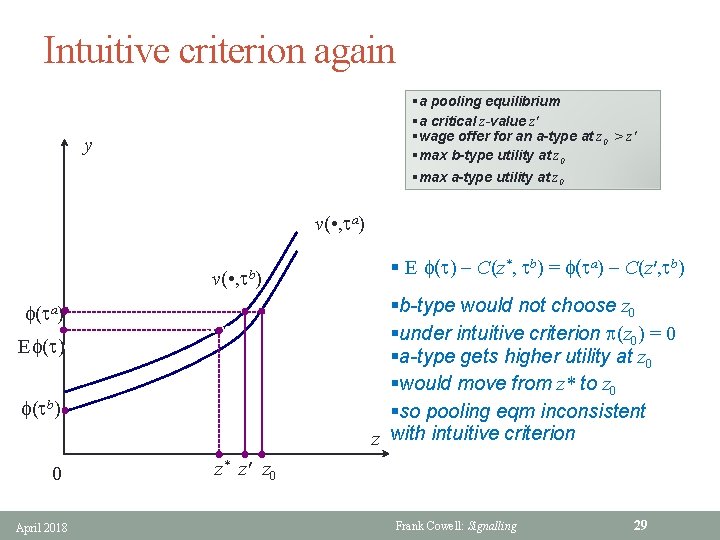
Intuitive criterion again §a pooling equilibrium §a critical z-value z' §wage offer for an a-type at z 0 > z' §max b-type utility at z 0 §max a-type utility at z 0 y v( • , ta) v( • , tb) §b-type would not choose z 0 §under intuitive criterion p(z 0) = 0 §a-type gets higher utility at z 0 §would move from z* to z 0 §so pooling eqm inconsistent z with intuitive criterion f(ta) Ef(t) f(tb) 0 April 2018 § E f(t) C(z*, tb) = f(ta) C(z′, tb) z* z' z 0 Frank Cowell: Signalling 29

Overview Signalling Costly signals: model An argument by example Costly signals: equilibrium Costless signals April 2018 Frank Cowell: Signalling 30

Costless signals: an example § Present the issue with a simplified example • general treatments can be difficult § N risk-neutral agents share in a project with output • q = a[z 1×z 2×z 3×. . . ] where 0 < α < 1 • zh = 0 or 1 is participation indicator of agent h § Agent h has cost of participation ch (unknown to others) • ch [0, 1] • it is common knowledge that prob(ch ≤ c) = c § Output is a public good, so net payoff to each agent h is • q ch § Consider this as a simultaneous-move game • what is the NE? • improve on NE by making announcements before the game starts? April 2018 Frank Cowell: Signalling 31

Example: NE without signals § Central problem: each h risks incurring cost ch while getting consumption 0 § If π is probability that any other agent participates, payoff to h is • a −ch with probability [p]N− 1 • −ch otherwise § Expected payoff to h is a[p]N− 1 − ch § Probability that expected payoff is positive is a[p]N− 1 • but this is the probability that agent h actually participates • therefore p = a[p]N− 1 • this can only be satisfied if p = 0 § So the NE is zh = 0 for all h, as long as α < 1 April 2018 Frank Cowell: Signalling 32

Example: introduce signals § Introduce a preliminary stage to the game § Each agent has the opportunity to signal his intention: • each agent announces [YES] or [NO] to the others • each agent then decides whether or not to participate § Then there is an equilibrium in which the following occurs • each h announces [YES] if and only if ch < α • h selects zh = 1 iff all agents have announced [YES] § In this equilibrium: • agents don’t risk wasted effort • if there are genuine high-cost ch agents present that inhibit the project • this will be announced at the signalling stage April 2018 Frank Cowell: Signalling 33

Signalling: summary § Both costly and costless signals are important § Costly signals: • separating PBE not unique? • intuitive criterion suggests out-of-equilibrium beliefs • pooling equilibrium may not be unique • inconsistent with intuitive criterion? § Costless signals: • a role to play in before the game starts April 2018 Frank Cowell: Signalling 34