Prerequisites Almost essential General equilibrium Basics Frank Cowell

Prerequisites Almost essential General equilibrium: Basics Frank Cowell: Microeconomics Useful, but optional General Equilibrium: Price Taking November 2006 General Equilibrium: Excess Demand the Rôle of Prices MICROECONOMICS Principles and Analysis Frank Cowell

Some unsettled questions Frank Cowell: Microeconomics n n n Under what circumstances can we be sure that an equilibrium exists? Will the economy somehow “tend” to this equilibrium? And will this determine the price system for us? We will address these using the standard model of a general-equilibrium system To do this we need just one more new concept.

Overview. . . Frank Cowell: Microeconomics General Equilibrium: Excess Demand+ Excess Demand Functions Definition and properties Equilibrium Issues Prices and Decentralisation

Frank Cowell: Microeconomics Ingredients of the excess demand function Aggregate demands (the sum of individual households' demands) n Aggregate net-outputs (the sum of individual firms' net outputs). n Resources n Incomes determined by prices n check this out

Aggregate consumption, net output Frank Cowell: Microeconomics Consumer: Aggregation Firm and the market h. From household’s demand function § Because incomes depend on prices xih = Dih(p, yh) = Dih(p, yh(p) ) h. So demands are just functions of p § xih( • ) depends on holdings xih = xih(p) of resources and shares h. If all goods are private (rival) then aggregate demands can be written: xi(p) = Sh xih(p) h. From firm’s supply of net output qif = qif(p) h. Aggregate: qi = Sf qif(p) § “Rival”: extra consumers require additional resources. Same as in “consumer: aggregation” § standard supply functions/ demand for inputs graphical § aggregation is valid if there summary are no externalities. Just as in “Firm and the market”)

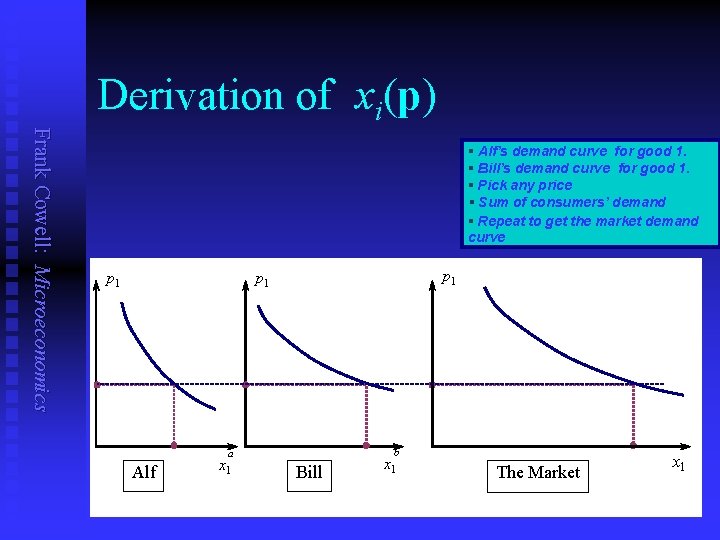
Derivation of xi(p) Frank Cowell: Microeconomics § Alf’s demand curve for good 1. § Bill’s demand curve for good 1. § Pick any price § Sum of consumers’ demand § Repeat to get the market demand curve p 1 p 1 b a Alf x 1 Bill x 1 The Market x 1

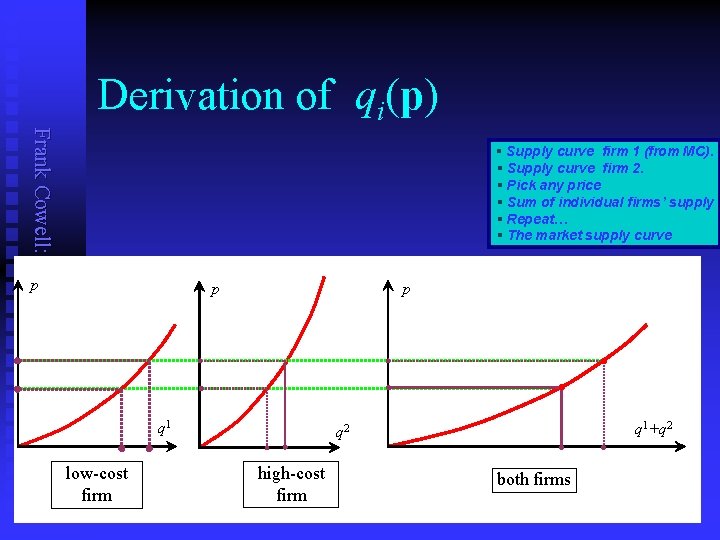
Derivation of qi(p) Frank Cowell: Microeconomics § Supply curve firm 1 (from MC). § Supply curve firm 2. § Pick any price § Sum of individual firms’ supply § Repeat… § The market supply curve p p p q 1 low-cost firm q 1+q 2 high-cost firm both firms

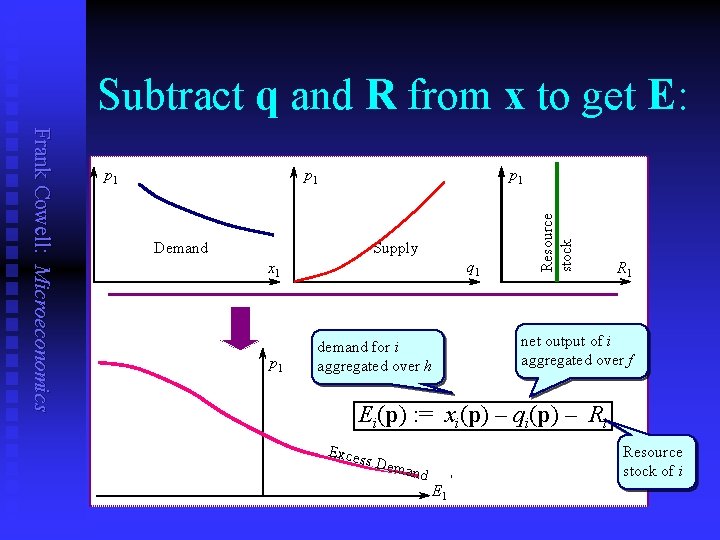
Subtract q and R from x to get E: p 1 Demand Supply q 1 x 1 p 1 Resource stock Frank Cowell: Microeconomics p 1 R 1 net output of i aggregated over f demand for i aggregated over h Ei(p) : = xi(p) – qi(p) – Ri Exces s Dem and 1 E 1 Resource stock of i

Frank Cowell: Microeconomics Equilibrium in terms of Excess Demand Equilibrium is characterised by a price vector p* 0 such that: • For every good i: Ei(p*) 0 • For each good i that has a positive price in equilibrium (i. e. if pi* > 0): Ei(p*) = 0 The materials balance condition (dressed up a bit) If this is violated, then somebody, somewhere isn't maximising. . . You can only have excess supply of a good in equilibrium if the price of that good is 0.

Using E to find the equilibrium Frank Cowell: Microeconomics n n Five steps to the equilibrium allocation 1. From technology compute firms’ net output functions and profits. 2. From property rights compute household incomes and thus household demands. 3. Aggregate the xs and qs and use x, q, R to compute E Find p* as a solution to the system of E functions 4. 5. Plug p* into demand functions and net output functions to get the allocation But this begs some questions about step 4

Issues in equilibrium analysis Frank Cowell: Microeconomics n Existence u n Uniqueness u n Is there only one p*? Stability u n Is there any such p*? Will p “tend to” p*? For answers we use some fundamental properties of E.

Two fundamental properties. . . Frank Cowell: Microeconomics Link to consumer demand • Walras’ Law. For any price p: You only have to work with n-1 (rather than n) equations n Si=1 pi Ei(p) = 0 Hint #1: think about the "adding-up" property of demand functions. . . • Homogeneity of degree 0. For any price p and any t > 0 : Ei(tp) = Ei(p) You can normalise the prices by any positive number Hint #2: think about the homogeneity property of demand functions. . . Can you explain why they are true? Reminder : these hold for any competitive allocation, not just equilibrium

Price normalisation Frank Cowell: Microeconomics n n We may need to convert from n numbers p 1, p 2, …pn to n 1 relative prices. The precise method is essentially arbitrary. The choice of method depends on the purpose of your model. It can be done in a variety of ways: You could divide by n a numéraire pppn to give a labour Mars. Bar pi S i=1 neat oftheory nthat -1 prices standard value system “Marxian” Mars bar theory of ofvalue set of set prices sum to 1 § This method might seem weird § But it has a nice property. § The set of all normalised prices is convex and compact.

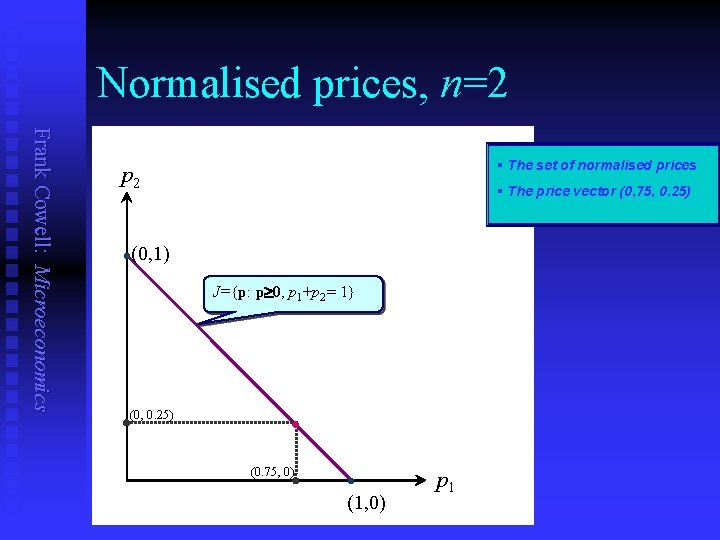
Normalised prices, n=2 Frank Cowell: Microeconomics § The set of normalised prices p 2 l § The price vector (0, 75, 0. 25) (0, 1) J={p: p 0, p 1+p 2 = 1} (0, 0. 25) • (0. 75, 0) l (1, 0) p 1

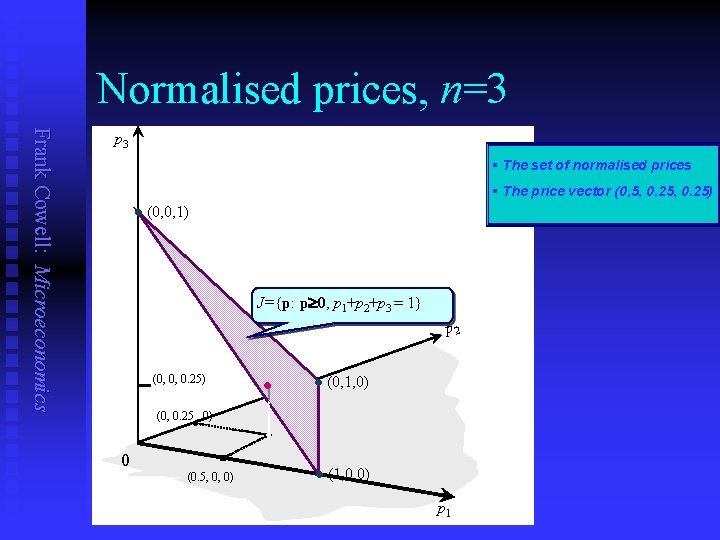
Normalised prices, n=3 Frank Cowell: Microeconomics p 3 § The set of normalised prices § The price vector (0, 5, 0. 25) l (0, 0, 1) J={p: p 0, p 1+p 2+p 3 = 1} p 2 (0, 0, 0. 25) • l (0, 1, 0) l (1, 0, 0) (0, 0. 25 , 0) 0 (0. 5, 0, 0) p 1

Overview. . . Frank Cowell: Microeconomics General Equilibrium: Excess Demand+ Excess Demand Functions Is there any p*? Equilibrium Issues Prices and Decentralisation • Existence • Uniqueness • Stability

Approach to the existence problem Frank Cowell: Microeconomics n Imagine a rule that moves prices in the direction of excess demand: u u u n n This rule uses the E-functions to map the set of prices into itself. An equilibrium exists if this map has a “fixed point. ” u n a p* that is mapped into itself? To find the conditions for this, use normalised prices u u n “if Ei >0, increase pi” “if Ei <0 and pi >0, decrease pi” An example of this under “stability” below. p J. J is a compact, convex set. We can examine this in the special case n = 2. u In this case normalisation implies that p 2 º 1 p 1.

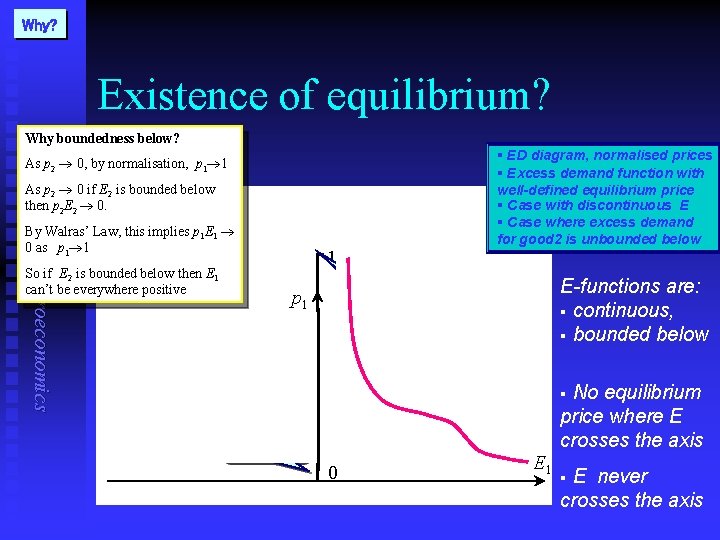
Why? Existence of equilibrium? Frank Cowell: Microeconomics Why boundedness below? § ED diagram, normalised prices § Excess demand function with well-defined equilibrium price § Case with discontinuous E § Case where excess demand for good 2 is unbounded below As p 2 0, by normalisation, p 1 1 As p 2 0 if E 2 is bounded below then p 2 E 2 0. By Walras’ Law, this implies p 1 E 1 0 as p 1 1 So if E 2 is bounded below then E 1 can’t be everywhere positive 1 p 1 Excess supply good 2 is free here l good 1 is free here E-functions are: § continuous, § bounded below p 1* 0 Excess demand No equilibrium price where E crosses the axis § E 1 E never crosses the axis §

Existence: a basic result Frank Cowell: Microeconomics n An equilibrium price vector must exist if: 1. 2. u n Boundedness is no big deal. u n excess demand functions are continuous and bounded from below. (“continuity” can be weakened to “upper-hemicontinuity”). Can you have infinite excess supply. . . ? However continuity might be tricky. u u Let's put it on hold. We examine it under “the rôle of prices”

Overview. . . Frank Cowell: Microeconomics General Equilibrium: Excess Demand+ Excess Demand Functions Is there just one p*? Equilibrium Issues Prices and Decentralisation • Existence • Uniqueness • Stability

The uniqueness problem Frank Cowell: Microeconomics n n Multiple equilibria imply multiple allocations, at normalised prices. . . with reference to a given property distribution. Will not arise if the E-functions satisfy WARP. If WARP is not satisfied this can lead to some startling behaviour. . . let's see

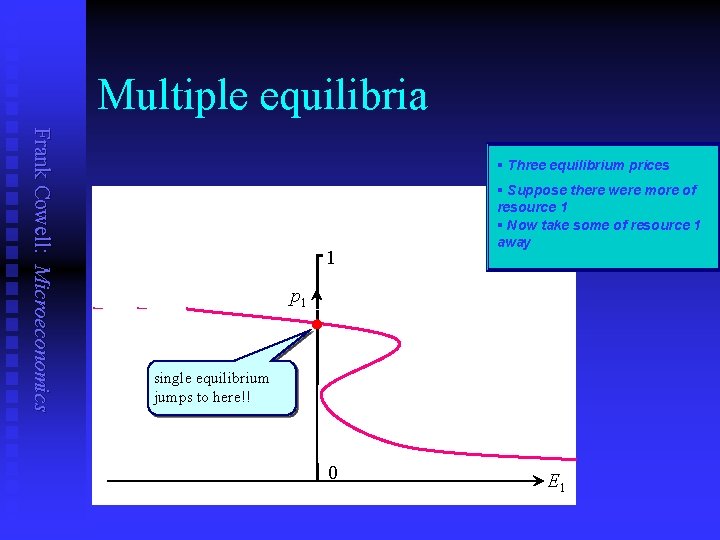
Multiple equilibria Frank Cowell: Microeconomics § Three equilibrium prices § Suppose there were more of resource 1 § Now take some of resource 1 away 1 p 1 single equilibrium jumps to here!! three equilibria degenerate to one! 0 E 1

Overview. . . Frank Cowell: Microeconomics General Equilibrium: Excess Demand+ Excess Demand Functions Will the system tend to p*? Equilibrium Issues Prices and Decentralisation • Existence • Uniqueness • Stability

Stability analysis Frank Cowell: Microeconomics n n We can model stability similar to physical sciences We need. . . u u u n A definition of equilibrium A process Initial conditions Main question is to identify these in economic terms Simple example

A stable equilibrium Frank Cowell: Microeconomics Stable: Equilibrium: If we apply a small shock Status quo isadjustment left the built-in undisturbed by gravity process (gravity) restores the status quo

An unstable equilibrium Frank Cowell: Microeconomics Equilibrium: Unstable: This If weactually apply afulfils small the shock definition. the built-in adjustment process (gravity) moves us But…. away from the status quo

“Gravity” in the CE model Frank Cowell: Microeconomics n n Imagine there is an auctioneer to announce prices, and to adjust if necessary. If good i is in excess demand, increase its price. If good i is in excess supply, decrease its price (if it hasn't already reached zero). Nobody trades till the auctioneer has finished.

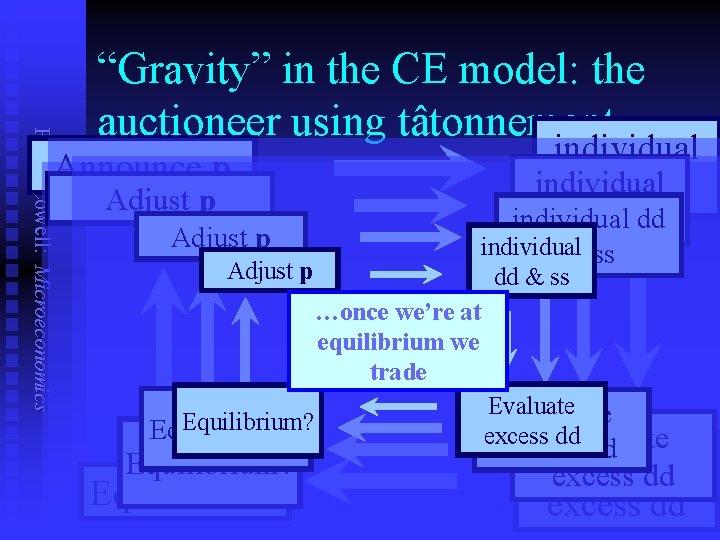
Frank Cowell: Microeconomics “Gravity” in the CE model: the auctioneer using tâtonnement individual dd & ss Announce p Adjust p individual dd & ssdd individual & ss dd & ss …once we’re at equilibrium we trade Equilibrium? Evaluate excess dd

Adjustment and stability Frank Cowell: Microeconomics n Adjust prices according to sign of Ei: u u If Ei > 0 then increase pi If Ei < 0 and pi > 0 then decrease pi n A linear tâtonnement adjustment mechanism: n Define distance d between p(t) and equilibrium p* n Given WARP, d falls with t under tâtonnement Two examples: with/without WARP

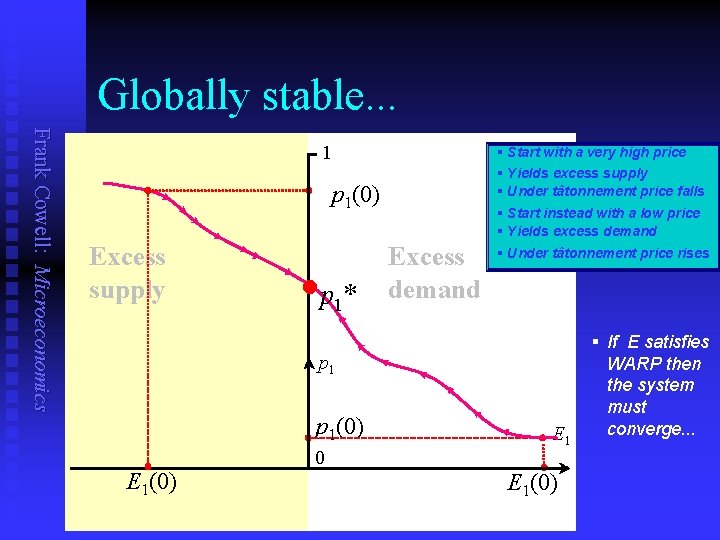
Globally stable. . . Frank Cowell: Microeconomics 1 p 1(0) Excess supply • p * 1 Excess demand § Start with a very high price § Yields excess supply § Under tâtonnement price falls § Start instead with a low price § Yields excess demand § Under tâtonnement price rises § If E satisfies p 1(0) E 1(0) 0 E 1(0) WARP then the system must converge. . .

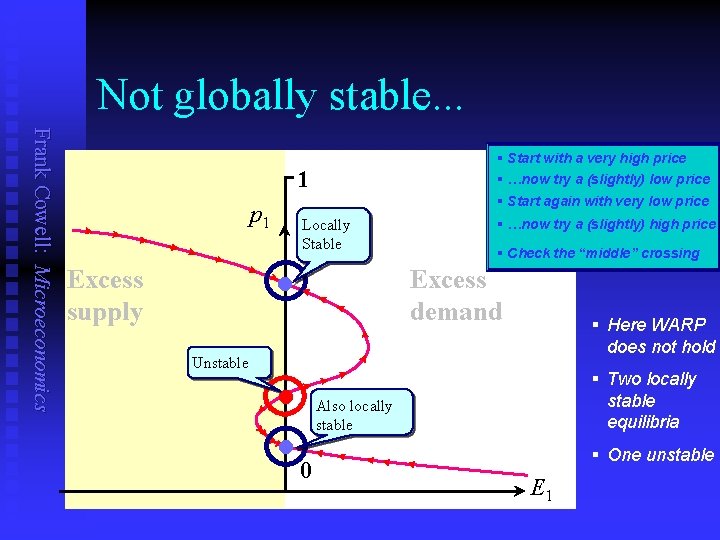
Not globally stable. . . Frank Cowell: Microeconomics § Start with a very high price § …now try a (slightly) low price 1 § Start again with very low price p 1 • Excess supply Unstable Locally Stable § …now try a (slightly) high price § Check the “middle” crossing Excess demand § Here WARP does not hold • • 0 § Two locally stable equilibria Also locally stable § One unstable E 1

Overview. . . Frank Cowell: Microeconomics General Equilibrium: Excess Demand+ Excess Demand Functions The separation theorem and the role of large numbers Equilibrium Issues Prices and Decentralisation

Decentralisation Frank Cowell: Microeconomics Link to Crusoe: Link to Firm and market n Recall the important result on decentralisation u n n The counterpart is true for this multi-person world. Requires assumptions about convexity of two sets, defined at the aggregate level: u u n discussed in the case of Crusoe’s island the “attainable set”: A : = {x: x £ q+R, F(q) 0 } the “better-than” set: B(x*) : = {Shxh: Uh(xh ) Uh(x*h ) } To see the power of the result here… u u use an “averaging” argument previously used in lectures on the firm

Decentralisation again Frank Cowell: Microeconomics § The attainable set § The “Better-than-x* ” set § The price line § Decentralisation x 2 x* B p 1 § A = {x: x q+R, F(q) 0} § B = {Shxh: Uh(xh) Uh(x*h)} § x* maximises income over A § x* minimises expenditure over B p 2 A 0 x 1

Problems with prices Frank Cowell: Microeconomics n n n Either non-convex technology (increasing returns or other indivisibilities) for some firms, or. . . non-convexity of B-set (non-concave- contoured preferences) for some households. . . may imply discontinuous excess demand function and so. . . absence of equilibrium. But if there are large numbers of agents everything may be OK. two examples

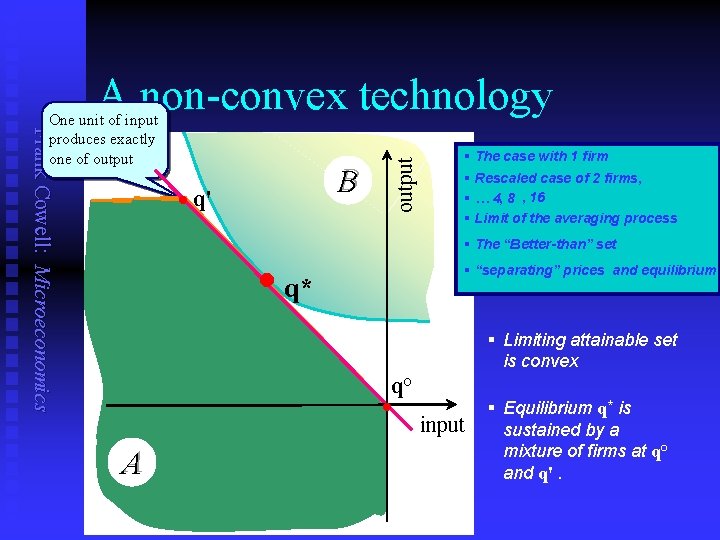
Frank Cowell: Microeconomics One unit of input produces exactly one of output B q' output A non-convex technology § The case with 1 firm § Rescaled case of 2 firms, § … 4, 8 , 16 § Limit of the averaging process § The “Better-than” set • q* § “separating” prices and equilibrium § Limiting attainable set is convex A q° input § Equilibrium q* is sustained by a mixture of firms at q° and q'.

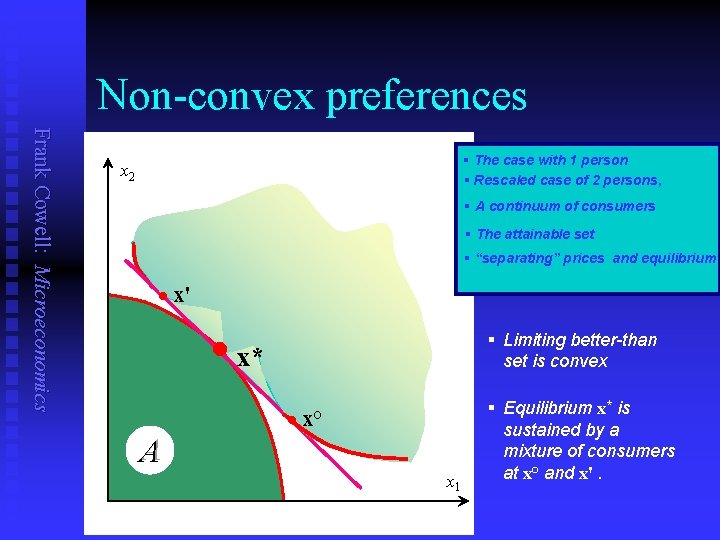
Non-convex preferences Frank Cowell: Microeconomics § The case with 1 person § Rescaled case of 2 persons, x 2 § A continuum of consumers § The attainable set No equilibrium here § “separating” prices and equilibrium x' • x* § Limiting better-than B set is convex § Equilibrium x* is x° A x 1 sustained by a mixture of consumers at x° and x'.

Summary Frank Cowell: Microeconomics n Excess demand functions are handy tools for getting results Review n Continuity and boundedness ensure existence of equilibrium Review n WARP ensures uniqueness and stability Review n But requirements of continuity may be demanding Review