Prerequisites Almost essential Welfare Basics Welfare Efficiency WELFARE

Prerequisites Almost essential Welfare: Basics Welfare: Efficiency WELFARE: THE SOCIALWELFARE FUNCTION MICROECONOMICS Principles and Analysis Frank Cowell April 2018 Frank Cowell: Welfare - Social Welfare function 1

Social Welfare Function § Limitations of the welfare analysis so far: § Constitution approach • Arrow theorem – is the approach overambitious? § General welfare criteria • efficiency – nice but indecisive • extensions – contradictory? § SWF is our third attempt • something like a simple utility function…? Requirements April 2018 Frank Cowell: Welfare - Social Welfare function 2

Overview Welfare: SWF The Approach What is special about a social-welfare function? SWF: basics SWF: national income SWF: income distribution April 2018 Frank Cowell: Welfare - Social Welfare function 3

The SWF approach § Restriction of “relevant” aspects of social state to each person (household) § Knowledge of preferences of each person (household) § Comparability of individual utilities • utility levels • utility scales § An aggregation function W for utilities • contrast with constitution approach • there we were trying to aggregate orderings A sketch of the approach April 2018 Frank Cowell: Welfare - Social Welfare function 4

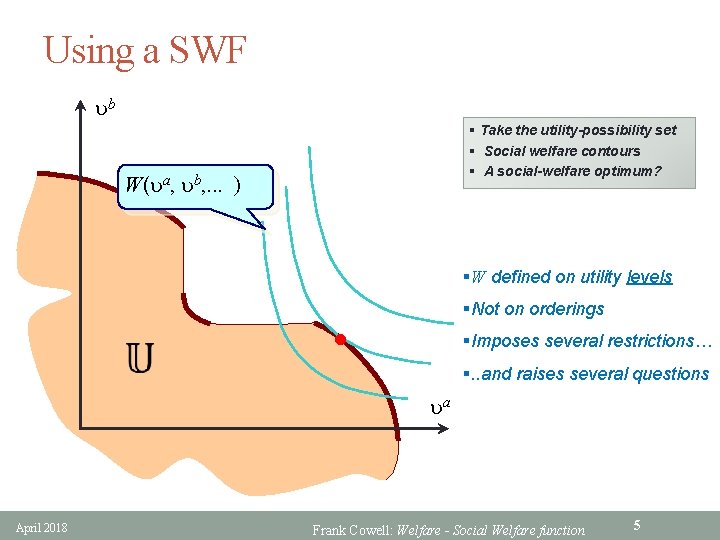
Using a SWF ub § Take the utility-possibility set § Social welfare contours § A social-welfare optimum? W(ua, ub, . . . ) §W defined on utility levels §Not on orderings • §Imposes several restrictions… §. . and raises several questions ua April 2018 Frank Cowell: Welfare - Social Welfare function 5

Issues in SWF analysis § What is the ethical basis of the SWF? § What should be its characteristics? § What is its relation to utility? § What is its relation to income? April 2018 Frank Cowell: Welfare - Social Welfare function 6

Overview Welfare: SWF The Approach Where does the social-welfare function come from? SWF: basics SWF: national income SWF: income distribution April 2018 Frank Cowell: Welfare - Social Welfare function 7

An individualistic SWF § The standard form expressed thus W(u 1, u 2, u 3, . . . ) • an ordinal function • defined on space of individual utility levels • not on profiles of orderings § But where does W come from. . . ? § We'll check out two approaches: • the equal-ignorance assumption • the PLUM principle April 2018 Frank Cowell: Welfare - Social Welfare function 8

1: The equal ignorance approach § Suppose the SWF is based on individual preferences. § Preferences are expressed behind a “veil of ignorance” § It works like a choice amongst lotteries • don't confuse w and q! § Each individual has partial knowledge: • knows the distribution of allocations in the population • knows the utility implications of the allocations • knows the alternatives in the Great Lottery of Life • does not know which lottery ticket he/she will receive April 2018 Frank Cowell: Welfare - Social Welfare function 9

“Equal ignorance”: formalisation § Individualistic welfare: payoffs if assigned identity 1, 2, 3, . . . in the Lottery of Life W(u 1, u 2, u 3, . . . ) § v. N-M form of utility function: åwÎW pw u(xw) Equivalently: åwÎW pw uw § Replace W by set of identities {1, 2, . . . nh}: å h p h uh § A suitable assumption about “probabilities”? 1 nh W = — å uh nh April 2018 use theory of choice under uncertainty to find shape of W pw: probability assigned to w u : cardinal utility function, independent of w uw: utility payoff in state w welfare is expected utility from a "lottery on identity“ An additive form of the welfare function h=1 Frank Cowell: Welfare - Social Welfare function 10

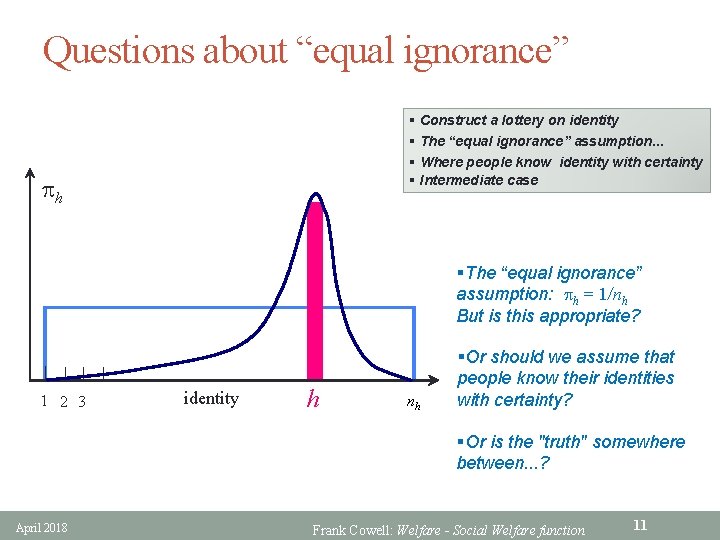
Questions about “equal ignorance” § Construct a lottery on identity § The “equal ignorance” assumption. . . § Where people know identity with certainty § Intermediate case ph §The “equal ignorance” assumption: ph = 1/nh But is this appropriate? | | | 1 2 3 | | identity h nh §Or should we assume that people know their identities with certainty? §Or is the "truth" somewhere between. . . ? April 2018 Frank Cowell: Welfare - Social Welfare function 11

2: The PLUM principle § Now for the second rather cynical approach § Acronym stands for People Like Us Matter § Whoever is in power may impute: • either their own views • or what they think “society’s” views are • or what they think “society’s” views ought to be • probably based on the views of those in power § There’s a branch of modern microeconomics that is a reinvention of classical “Political Economy” • concerned with the interaction of political decision-making and economic outcomes • but beyond our present course April 2018 Frank Cowell: Welfare - Social Welfare function 12

Overview Welfare: SWF The Approach Conditions for a welfare maximum SWF: basics SWF: national income SWF: income distribution April 2018 Frank Cowell: Welfare - Social Welfare function 13

The SWF maximum problem § Take the individualistic welfare model Standard assumption § Assume everyone is selfish: my utility depends only on my bundle § Substitute in the above: Gives SWF in terms of the allocation W(u 1, u 2, u 3, . . . ) uh = Uh(xh) , h = 1, 2, . . . , nh W(U 1(x 1), U 2(x 2), U 3(x 3), . . . ) a quick sketch April 2018 Frank Cowell: Welfare - Social Welfare function 14

From an allocation to social welfare (x 1 a, x 2 a) (x 1 b, x 2 b) § From the attainable set. . . §. . . take an allocation § Evaluate utility for each agent A A § Plug into W to get social welfare ua=Ua(x 1 a, x 2 a) ub=Ub(x 1 b, x 2 b) § But what happens to welfare if we vary the allocation in A? W(ua, ub) April 2018 Frank Cowell: Welfare - Social Welfare function 15

Varying the allocation § Differentiate w. r. t. xih : duh = Uih(xh) dxih § Sum over i: The effect on h if commodity i is changed marginal utility derived by h from good i n duh = S Uih(xh) dxih The effect on h if all commodities are changed i=1 § Differentiate W with respect to uh: nh d. W = S Wh duh marginal impact on social welfare of h’s utility h=1 § Substitute nfor dunh in the above: d. W = S Wh S Uih(xh) dxih h h=1 Weights from the SWF April 2018 Changes in utility change social welfare. i=1 So changes in allocation change welfare. Weights from utility function Frank Cowell: Welfare - Social Welfare function 16

Use this to characterise a welfare optimum § Write down SWF, defined on individual utilities § Introduce feasibility constraints on overall consumptions § Set up the Lagrangian § Solve in the usual way Now for the maths April 2018 Frank Cowell: Welfare - Social Welfare function 17

The SWF maximum problem § First component of the problem: W(U 1(x 1), U 2(x 2), U 3(x 3), . . . ) The objective function Utility depends on own consumption Individualistic welfare § Second component of the problem: n F(x) £ 0, xi = Sh=1 xih Feasibility constraint § The Social-welfare Lagrangian: n 1 1 2 2 W(U (x ), . . . ) - l. F (Sh=1 xh ) Constraint subsumes technological feasibility and materials balance § FOCs for an interior maximum: Wh (. . . ) Uih(xh) − l. Fi(x) = 0 From differentiating Lagrangean with respect to xih § And if xih = 0 at the optimum: Wh (. . . ) Uih(xh) − l. Fi(x) £ 0 Usual modification for a corner solution h All goods are private h April 2018 Frank Cowell: Welfare - Social Welfare function 18

Solution to SWF maximum problem § From FOCs: Any pair of goods, i, j Any pair of households h, ℓ MRS equated across all h Uih(xh) Uiℓ(xℓ) ——— = ——— Ujh(xh) Ujℓ(xℓ) We’ve met this condition before - Pareto efficiency § Also from the FOCs: Wh Uih(xh) = Wℓ Uiℓ(xℓ) § Relate marginal utility to prices: Uih(xh) = Vy hp i social marginal utility of toothpaste equated across all h This is valid if all consumers optimise Marginal utility of money § Substituting into the above: Wh V y h = Wℓ V y ℓ April 2018 Social marginal utility of income At optimum the welfare value of $1 is equated across all h. Call this common value M Frank Cowell: Welfare - Social Welfare function 19

To focus on main result. . . § Look what happens in neighbourhood of optimum § Assume that everyone is acting as a maximiser • firms • households § Check what happens to the optimum if we alter incomes or prices a little § Similar to looking at comparative statics for a single agent April 2018 Frank Cowell: Welfare - Social Welfare function 20

Changes in income, social welfare § Social welfare can be expressed as: W(U 1(x 1), U 2(x 2), . . . ) = W(V 1(p, y 1), V 2(p, y 2), . . . ) SWF in terms of direct utility. Using indirect utility function Changes in utility and change social welfare … § Differentiate the SWF w. r. t. {yh}: nh nh h=1 d. W = S Wh duh = S Wh. Vyh dyh nh d. W = M S dyh h=1 . . . related to income change in “national income” § Differentiate the SWF w. r. t. pi : nh nh h=1 d. W = S Wh. Vihdpi= – SWh. Vyh xihdpi nh d. W = – M S xihdpi h=1 April 2018 Changes in utility and change social welfare … from Roy’s identity Change in total expenditure . . . related to prices. . Frank Cowell: Welfare - Social Welfare function 21

An attractive result? § Summarising the results of the previous slide we have: § THEOREM: in the neighbourhood of a welfare optimum welfare changes are measured by changes in national income / national expenditure § But what if we are not in an ideal world? April 2018 Frank Cowell: Welfare - Social Welfare function 22

Overview Welfare: SWF The Approach A lesson from risk and uncertainty SWF: basics SWF: national income SWF: income distribution April 2018 Frank Cowell: Welfare - Social Welfare function 23

Derive a SWF in terms of incomes § What happens if the distribution of income is not ideal? • M is no longer equal for all h § Useful to express social welfare in terms of incomes § Do this by using indirect utility function V • express utility in terms of prices p and income y § Assume prices p are given § “Equivalise” (i. e. rescale) each income y • allow for differences in people’s needs • allow for differences in household size § Then you can write welfare as W(ya, yb, yc, … ) April 2018 Frank Cowell: Welfare - Social Welfare function 24

Income-distribution space: nh=2 § The income space: 2 persons Bill's income u e rfe e lin p of q te §An income distribution ty i l a c § Note the similarity with a diagram used in the analysis of uncertainty ·y 45° O April 2018 Alf's income Frank Cowell: Welfare - Social Welfare function 25

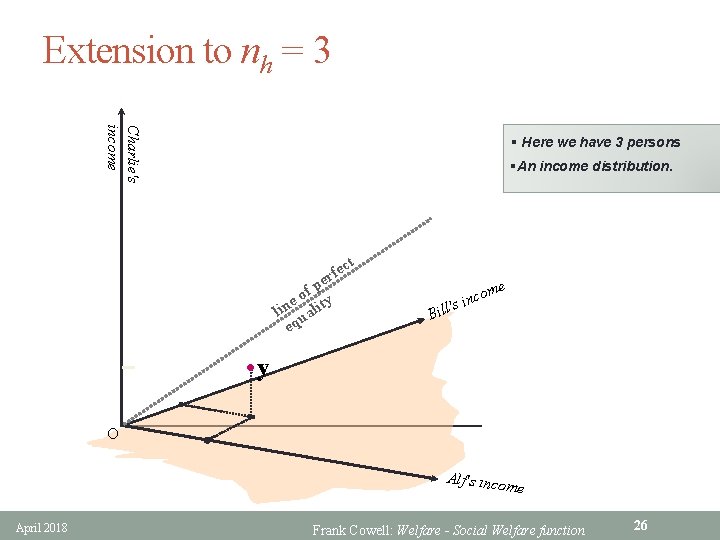
Extension to nh = 3 Charlie's income § Here we have 3 persons §An income distribution. ct e f er fp o y e lin ualit eq me o c 's in l l i B • y O Alf's inco me April 2018 Frank Cowell: Welfare - Social Welfare function 26

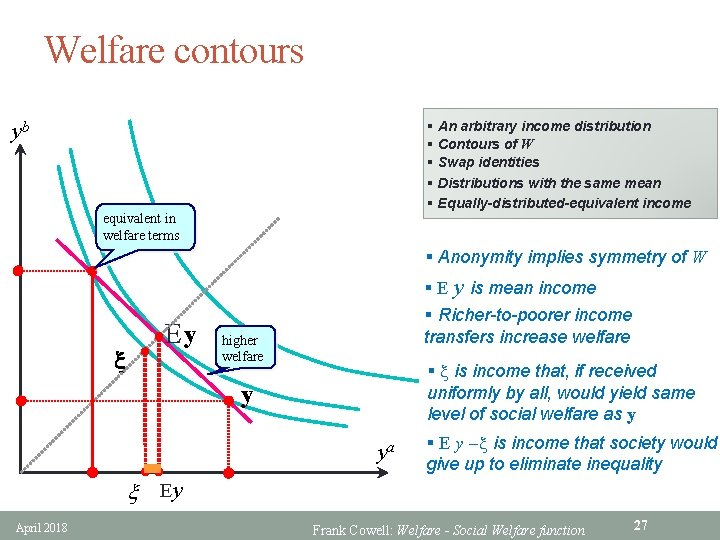
Welfare contours § An arbitrary income distribution § Contours of W § Swap identities § Distributions with the same mean § Equally-distributed-equivalent income yb equivalent in welfare terms § Anonymity implies symmetry of W x Ey § E y is mean income § Richer-to-poorer income transfers increase welfare higher welfare § x is income that, if received uniformly by all, would yield same level of social welfare as y y ya § E y x is income that society would give up to eliminate inequality x Ey April 2018 Frank Cowell: Welfare - Social Welfare function 27

A result on inequality aversion § Principle of Transfers : “a mean-preserving redistribution from richer to poorer should increase social welfare” § THEOREM: Quasi-concavity of W implies that social welfare respects the “Transfer Principle” April 2018 Frank Cowell: Welfare - Social Welfare function 28

Special form of the SWF § It can make sense to write W in the additive form W= nh 1 — S nh h=1 z(yh) • where the function z is the social evaluation function • (the 1/nh term is unnecessary – arbitrary normalisation) • Counterpart of u-function in choice under uncertainty § Can be expressed equivalently as an expectation: W = E z(yh) • where the expectation is over all identities • probability of identity h is the same, 1/nh , for all h § Constant relative-inequality aversion: 1 1–i z(y) = —— y 1–i • where i is the index of inequality aversion • works just like r, the index of relative risk aversion April 2018 Frank Cowell: Welfare - Social Welfare function 29

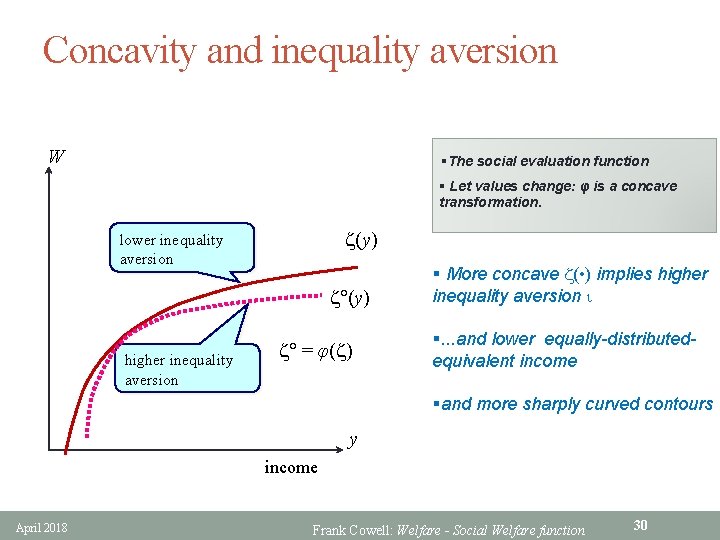
Concavity and inequality aversion W §The social evaluation function § Let values change: φ is a concave transformation. z(y) lower inequality aversion z (y) higher inequality aversion z = φ(z) § More concave z( • ) implies higher inequality aversion i §. . . and lower equally-distributedequivalent income §and more sharply curved contours y income April 2018 Frank Cowell: Welfare - Social Welfare function 30

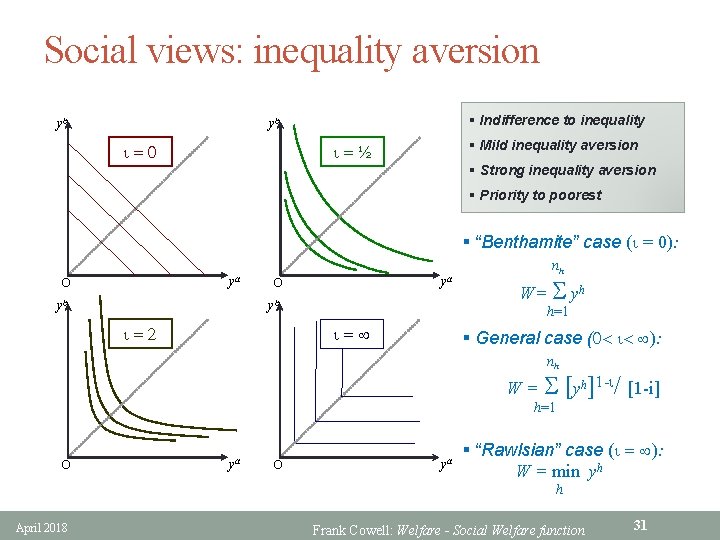
Social views: inequality aversion yb § Indifference to inequality yb § Mild inequality aversion i=½ i=0 § Strong inequality aversion § Priority to poorest § “Benthamite” case (i = 0): ya O yb i=2 nh W= S yh h=1 i= § General case (0< i< ): nh W = S [yh]1 -i/ [1 -i] h=1 O ya § “Rawlsian” case (i = ): W = min yh h April 2018 Frank Cowell: Welfare - Social Welfare function 31

Inequality, welfare, risk and uncertainty § There is a similarity of form between… • personal judgments under uncertainty • social judgments about income distributions § Likewise a logical link between risk and inequality § This could be seen as just a curiosity § Or as an essential component of welfare economics • Uses the “equal ignorance argument” § In the latter case the functions u and z should be taken as identical § “Optimal” social state depends crucially on shape of W • In other words the shape of z • Or the value of i April 2018 Frank Cowell: Welfare - Social Welfare function Three examples 32

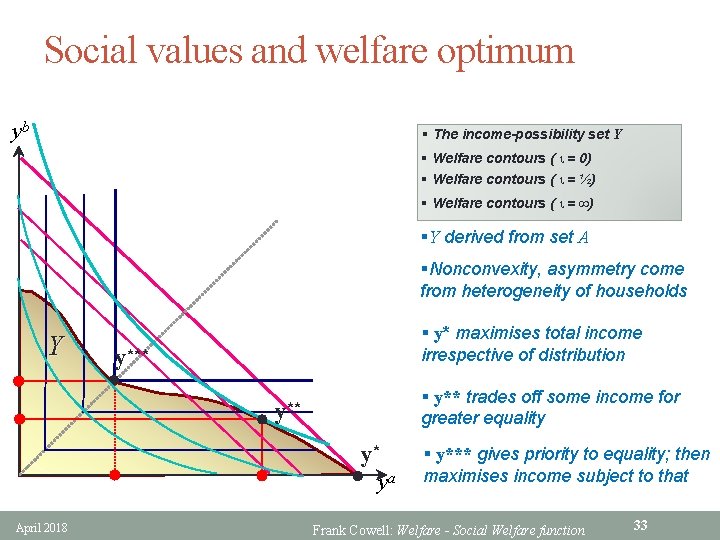
Social values and welfare optimum yb § The income-possibility set Y § Welfare contours ( i = 0) § Welfare contours ( i = ½) § Welfare contours ( i = ) §Y derived from set A §Nonconvexity, asymmetry come from heterogeneity of households Y § y* maximises total income irrespective of distribution y*** § y** trades off some income for greater equality y** y* ya April 2018 § y*** gives priority to equality; then maximises income subject to that Frank Cowell: Welfare - Social Welfare function 33

Summary The standard SWF is an ordering on utility levels § • • Analogous to an individual's ordering over lotteries Inequality- and risk-aversion are similar concepts In ideal conditions SWF is proxied by national income But for realistic cases two things are crucial: § § 1. 2. Information on social values Determining the income frontier Item 1 might be considered as beyond the scope of simple microeconomics Item 2 requires modelling of what is possible in the underlying structure of the economy § § • April 2018 which is what microeconomics is all about Frank Cowell: Welfare - Social Welfare function 34