Prerequisites Almost essential Welfare and Efficiency EFFICIENCY WASTE

Prerequisites Almost essential Welfare and Efficiency EFFICIENCY: WASTE MICROECONOMICS Principles and Analysis Frank Cowell: Efficiency-Waste

Agenda § Build on the efficiency presentation • Focus on relation between competition and efficiency § Start from the “standard” efficiency rules • MRS same for all households • MRT same for all firms • MRS=MRT for all pairs of goods § What happens if we depart from these rules? § How to quantify departures from efficiency? April 2018 Frank Cowell: Efficiency-Waste 2

Overview Efficiency: Waste Background How to evaluate inefficient states Basic model Model with production Applications April 2018 Frank Cowell: Efficiency-Waste 3

The approach § Use standard general equilibrium analysis to… • Model price distortion • Define reference set of prices § Use consumer welfare analysis to… • Model utility loss § Use standard analysis of household budgets to… • Model change in profits and rents April 2018 Frank Cowell: Efficiency-Waste 4

A reference point § Address the question: how much waste? § Need a reference point • where there is zero waste • quantify departures from this point § Any efficient point would do § But it is usual to take a CE allocation • gives us a set of prices • we’re not assuming it is the “default” state • just a convenient benchmark § Can characterise inefficiency as price distortion April 2018 Frank Cowell: Efficiency-Waste 5

A model of price distortion § § Assume there is a competitive equilibrium If so, then everyone pays the same prices But now we have a distortion What are the implications ~ for MRS and MRT? consumer prices April 2018 Distortion p 1 = p 1 [1+d] ~ p 2 = p 2 ~ p 3 = p 3 … = … ~ pn = pn Frank Cowell: Efficiency-Waste firms' prices 6

Price distortion: MRS and MRT § Consumption: § Production: • for commodities 2, 3, …, n • But for commodity 1… MRSij h MRT 1 j MRT 2 j pj = — pi pj = — [1+ d] p 1 pj = — p 2 pj MRT 3 j = — p 3 … … … pj MRTnj = — pn April 2018 For every household marginal rate of substitution = price ratio Frank Cowell: Efficiency-Waste Illustration… 7

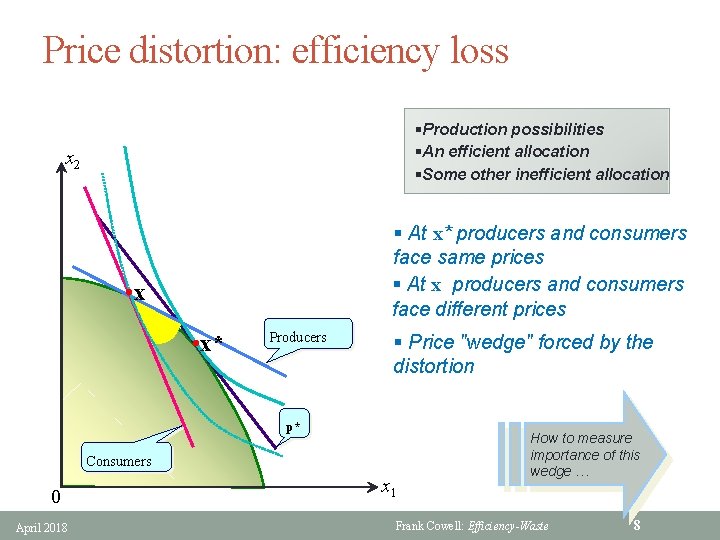
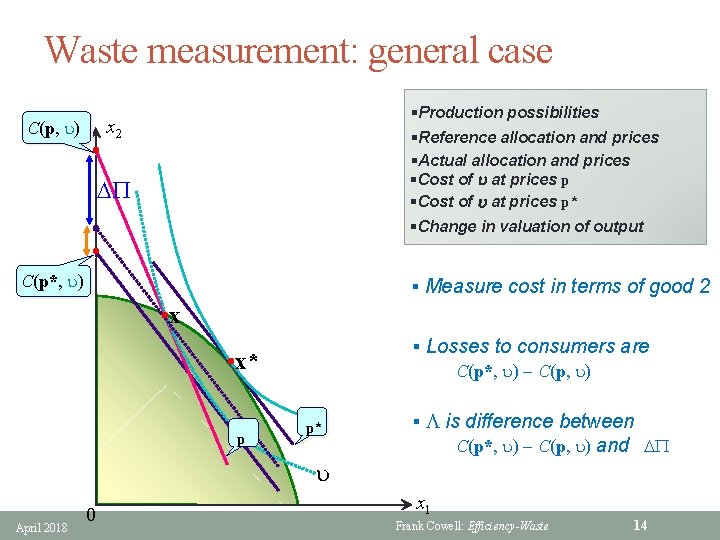
Price distortion: efficiency loss §Production possibilities §An efficient allocation §Some other inefficient allocation x 2 § At x* producers and consumers face same prices § At x producers and consumers face different prices • x* Producers § Price "wedge" forced by the distortion p* Consumers 0 April 2018 x 1 How to measure importance of this wedge … Frank Cowell: Efficiency-Waste 8

Waste measurement: a method § To measure loss we use a reference point § Take this as competitive equilibrium… • …which defines a set of reference prices § Quantify the effect of a notional price change: • Dpi : = pi – pi* • This is [actual price of i] – [reference price of i] § Evaluate the equivalent variation for household h : • EVh = Ch(p*, u h) – Ch(p, u h) – [y*h – yh] • This is D(consumer costs) – D(income) § Aggregate over agents to get a measure of loss, L • We do this for two cases… April 2018 Frank Cowell: Efficiency-Waste 9

Overview Efficiency: Waste Background Taking producer prices as constant… Basic model Model with production Applications April 2018 Frank Cowell: Efficiency-Waste 10

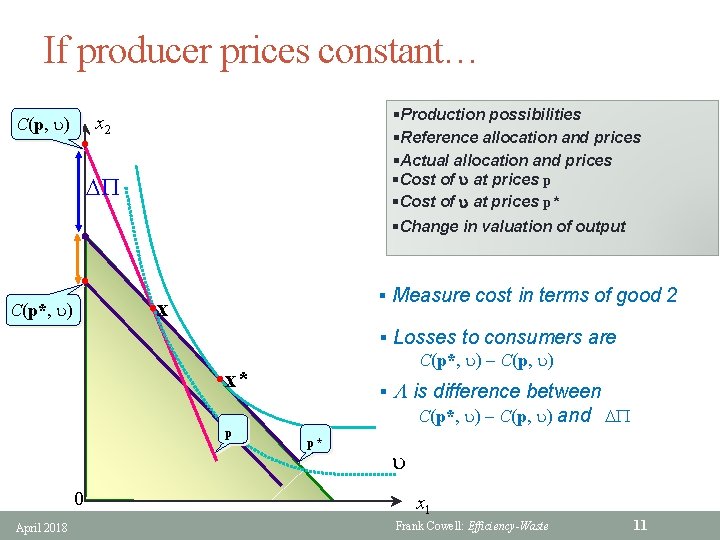
If producer prices constant… C(p, u) • §Production possibilities §Reference allocation and prices §Actual allocation and prices §Cost of u at prices p* x 2 DP §Change in valuation of output • § Measure cost in terms of good 2 • x C(p*, u) § Losses to consumers are C(p*, u) C(p, u) • x* p 0 April 2018 § L is difference between C(p*, u) C(p, u) and DP p* u x 1 Frank Cowell: Efficiency-Waste 11

Model with fixed producer prices § Waste L involves both demand supply responses § Simplify by taking case where production prices constant § Then waste is given by: § Use Shephard’s Lemma • xih = Hhi(p, uh) = Cih(p, uh) § Take a Taylor expansion to evaluate L: § L is a sum of areas under compensated demand curve April 2018 Frank Cowell: Efficiency-Waste 12

Overview Efficiency: Waste Background Allow supply-side response… Basic model Model with production Applications April 2018 Frank Cowell: Efficiency-Waste 13

Waste measurement: general case C(p, u) • §Production possibilities §Reference allocation and prices §Actual allocation and prices §Cost of u at prices p* x 2 DP §Change in valuation of output • C(p*, u) § Measure cost in terms of good 2 • x § Losses to consumers are C(p*, u) C(p, u) • x* p p* § L is difference between C(p*, u) C(p, u) and DP u April 2018 0 x 1 Frank Cowell: Efficiency-Waste 14

Model with producer price response § Adapt the L formula to allow for supply responses § Then waste is given by: • where qi (∙) is net supply function for commodity i § Again use Shephard’s Lemma and a Taylor expansion: April 2018 Frank Cowell: Efficiency-Waste 15

Overview Efficiency: Waste Background Working out the hidden cost of taxation and monopoly… Basic model Model with production Applications April 2018 Frank Cowell: Efficiency-Waste 16

Application 1: commodity tax § Commodity taxes distort prices • Take the model where producer prices are given • Let price of good 1 be forced up by a proportional commodity tax t • Use the standard method to evaluate waste • What is the relationship of tax to waste? § Simplified model: • identical consumers • no cross-price effects • (impact of tax on good 1 does not affect demand for other goods) § Use competitive, non-distorted case as reference April 2018 Frank Cowell: Efficiency-Waste 17

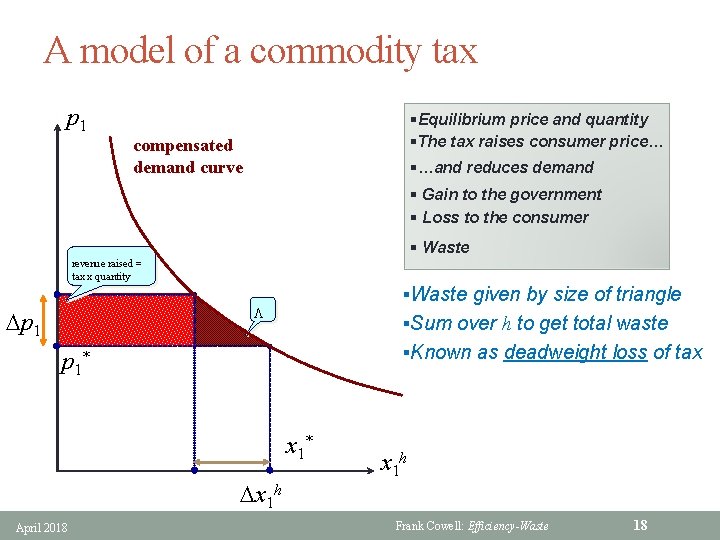
A model of a commodity tax p 1 §Equilibrium price and quantity §The tax raises consumer price… compensated demand curve §…and reduces demand § Gain to the government § Loss to the consumer § Waste revenue raised = tax x quantity §Waste given by size of triangle L Dp 1 §Sum over h to get total waste §Known as deadweight loss of tax p 1* x 1* Dx 1 h April 2018 x 1 h Frank Cowell: Efficiency-Waste 18

Tax: computation of waste § An approximation using Consumer’s Surplus § The tax imposed on good 1 forces a price wedge • Dp 1 = tp 1* > 0 where is p 1* is the untaxed price of the good § h’s demand for good 1 is lower with the tax: • x 1** rather than x 1* , where x 1** = x 1* + Dx 1 h and Dx 1 h < 0 § Revenue raised by government from h: • Th = tp 1* x 1**= x 1**Dp 1 > 0 § Absolute size of loss of consumer’s surplus to h is • |DCSh| = ∫ x 1 h dp 1 ≈ x 1** Dp 1 − ½ Dx 1 h. Dp 1 = Th − ½ t p 1* Dx 1 h > Th § Use the definition of elasticity e : = p 1 Dx 1 h / x 1 h. Dp 1< 0 § Net loss from tax (for h) is • Lh = |DCSh| − Th = − ½tp 1* Dx 1 h = − ½te. Dp 1 x 1** = − ½t e Th § Overall net loss from tax (for h) is • ½ |e| t. T • uses the assumption that all consumers are identical April 2018 Frank Cowell: Efficiency-Waste 19

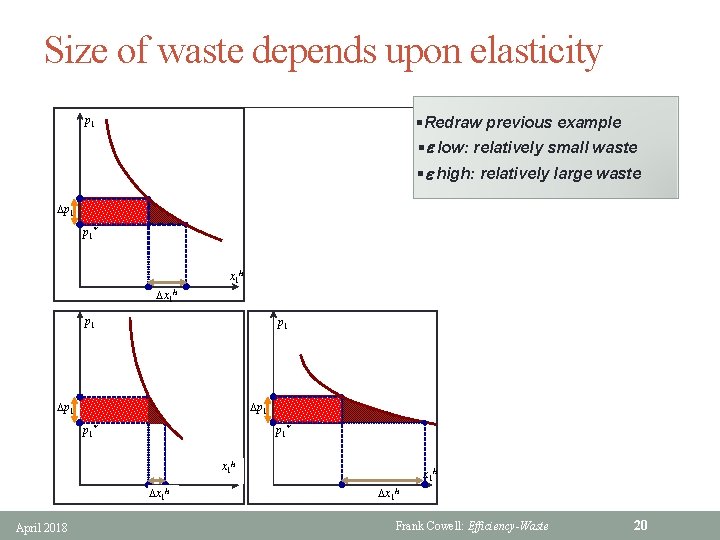
Size of waste depends upon elasticity p 1 §Redraw previous example compensated demand curve §e low: relatively small waste §e high: relatively large waste Dp 1 p 1* x 1 h Dp 1 Dx 1 h p 1 p 1* Dp 1 x 1 h Dx 1 h April 2018 x 1 h p 1* Dx 1 h Frank Cowell: Efficiency-Waste 20

Application 1: assessment § Waste inversely related to elasticity • Low elasticity: waste is small • High elasticity: waste is large § Suggests a policy rule • suppose required tax revenue is given • which commodities should be taxed heavily? • if you just minimise waste – impose higher taxes on commodities with lower elasticities § In practice considerations other than waste-minimisation will also influence tax policy • distributional fairness among households • administrative costs April 2018 Frank Cowell: Efficiency-Waste 21

Application 2: monopoly § Monopoly power is supposed to be wasteful • but why? § We know that monopolist: • charges price above marginal cost • so equilibrium solution is inefficient § But how inefficient? § Take simple version of main model • suppose markets for goods 2, …, n are competitive • good 1 is supplied monopolistically April 2018 Frank Cowell: Efficiency-Waste 22

Monopoly: computation of waste (1) § Monopoly power in market for good 1 forces a price wedge • Dp 1 = p 1** − p 1* > 0 where • p 1** is price charged in market • p 1* is marginal cost (MC) § h’s demand for good 1 is lower under this monopoly price: • x 1** = x 1* + Dx 1 h, • where Dx 1 h < 0 § Same argument as before gives: • loss imposed on household h: −½Dp 1 Dx 1 h > 0 • loss overall: − ½Dp 1 Dx 1, where x 1 is total output of good 1 • using definition of elasticity e, loss equals − ½Dp 12 e x 1**/p 1** § To evaluate this need to examine monopolist’s action… April 2018 Frank Cowell: Efficiency-Waste 23

Monopoly: computation of waste (2) § Monopolist chooses overall output • use first-order condition • MR = MC: § Evaluate MR in terms of price and elasticity: • p 1* * [ 1 + 1 / e] • FOC is therefore p 1* * [ 1 + 1 / e] = MC • hence Dp 1= p 1* * − MC = − p 1* * / e § Substitute into triangle formula to evaluate the loss: • ½ p 1* * x 1* * / |e| § Waste from monopoly is greater, the more inelastic is demand • highly inelastic demand: substantial monopoly power • highly elastic demand: approximates competition April 2018 Frank Cowell: Efficiency-Waste 24

Summary § Starting point: an “ideal” world • pure private goods, no externalities etc • so CE represents an efficient allocation § Characterise inefficiency in terms of price distortion • in the ideal world MRS = MRT for all h, f and all pairs of goods § Measure waste in terms of income loss • fine for individual • OK just to add up? § Extends to more elaborate models • straightforward in principle • but messy maths § Applications focus on simple practicalities • elasticities measuring consumers’ price response • but simple formulas conceal strong assumptions April 2018 Frank Cowell: Efficiency-Waste 25