Prerequisites Almost essential Consumner Optimisation Frank Cowell Microeconomics

Prerequisites Almost essential Consumner: Optimisation Frank Cowell: Microeconomics Useful, but optional Firm: Optimisation November 2006 A Simple Economy MICROECONOMICS Principles and Analysis Frank Cowell

The setting. . . Frank Cowell: Microeconomics n A closed economy u n A collection of natural resources u n Determines incomes A variety of techniques of production u n Prices determined internally Also determines incomes A single economic agent u R. Crusoe Needs new notation, new concepts. .

Notation and concepts Frank Cowell: Microeconomics available for consumption or production R = (R 1, R 2, . . . , Rn) q = (q 1, q 2, . . . , qn) §resources more on this soon. . . §net outputs just the same as before x = (x 1, x 2, . . . , xn) §consumption

Overview. . . Frank Cowell: Microeconomics Household Demand & Supply Structure of production Production in a multi-output, multi-process world The Robinson Crusoe problem Decentralisation Markets and trade

Net output clears up problems Frank Cowell: Microeconomics n “Direction” of production u n Ambiguity of some commodities u n Get a more general notation Is paper an input or an output? Aggregation over processes u How do we add my inputs and your outputs? We just need some reinterpretation

Approaches to outputs and inputs Frank Cowell: Microeconomics NET OUTPUTS OUTPUT INPUTS q 1 z 1 q 2 z 2 . . . qn-1 zm qn §A standard “accounting” approach §An approach using “net outputs” §How the two are related §A simple sign convention q q 1 –z 1 q 2 –z 2. . . =. . . qn-1 –zm qn +q Outputs: Inputs: + net additions to the stock of a good reductions in the stock of a good Intermediate 0 goods: your output and my input cancel each other out

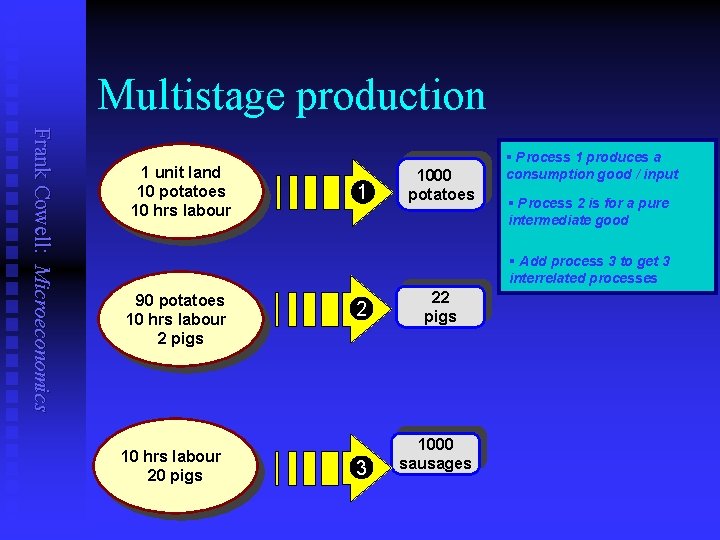
Multistage production Frank Cowell: Microeconomics 1 unit land 10 potatoes 10 hrs labour 1 1000 potatoes § Process 1 produces a consumption good / input § Process 2 is for a pure intermediate good § Add process 3 to get 3 interrelated processes 90 potatoes 10 hrs labour 2 pigs 10 hrs labour 20 pigs 2 3 22 pigs 1000 sausages

Combining the three processes Frank Cowell: Microeconomics Process 1 Process 3 Process 2 Economy’s net output vector sausages 0 0 +1000 potatoes +990 – 90 0 +900 pigs 0 labour – 10 – 30 land – 1 0 0 – 1 + 20 + – 20 0 = 30 hrs labour 1 unit land 22 pigs 1000 potatoes 1000 sausages

Frank Cowell: Microeconomics More about the potato-pig-sausage story n n n We have described just one technique What if more were available? What would be the concept of the isoquant? What would be the marginal product? What would be the trade-off between outputs?

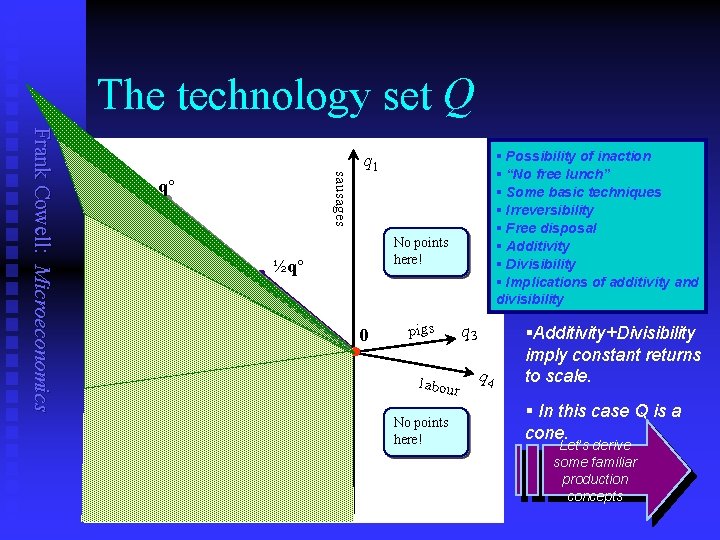
An axiomatic approach Frank Cowell: Microeconomics n Let Q be the set of all technically feasible net output vectors. u n n n The technology set. “q Q” means “q is technologically do-able” The shape of Q describes the nature of production possibilities in the economy. We build it up using some standard production axioms.

Standard production axioms Frank Cowell: Microeconomics n n n Possibility of Inaction u 0 Q No Free Lunch u Q R+n = {0} Irreversibility u Q (– Q ) = {0} Free Disposal u If q Q and q' q then q' Q Additivity u If q Q and q' Q then q + q' Q Divisibility u If q Q and 0 t 1 then tq Q A graphical interpretatio n

The technology set Q sausages Frank Cowell: Microeconomics q° 2 q' q'+q" q" All these points No points here! ½q° q' § Possibility of inaction § “No free lunch” § Some basic techniques § Irreversibility § Free disposal § Additivity § Divisibility § Implications of additivity and divisibility q 1 0 • pigs labour No points here! q 3 q 4 §Additivity+Divisibility imply constant returns to scale. § In this case Q is a cone. Let’s derive some familiar production concepts

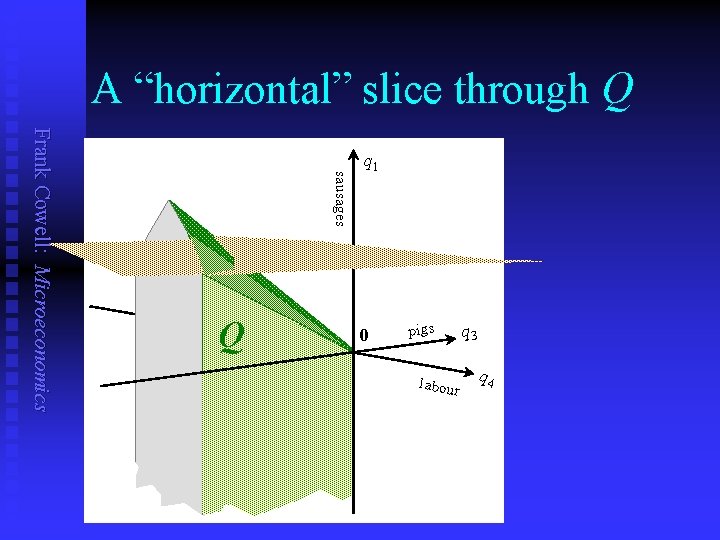
A “horizontal” slice through Q sausages Frank Cowell: Microeconomics Q q 1 0 pigs labour q 3 q 4

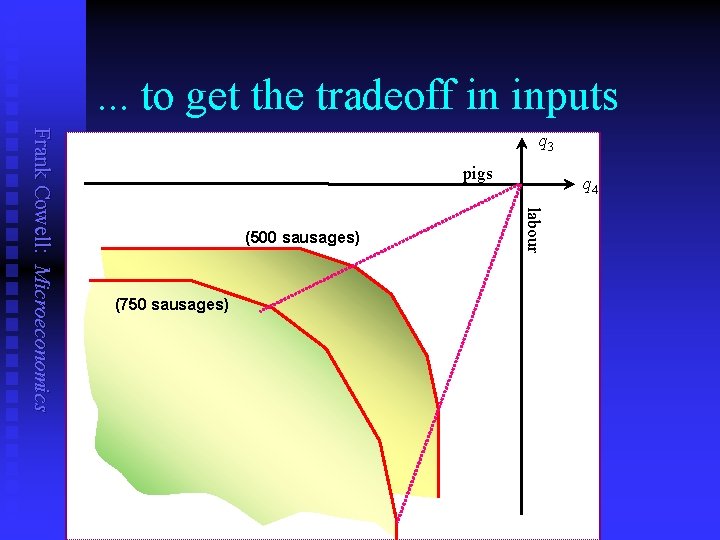
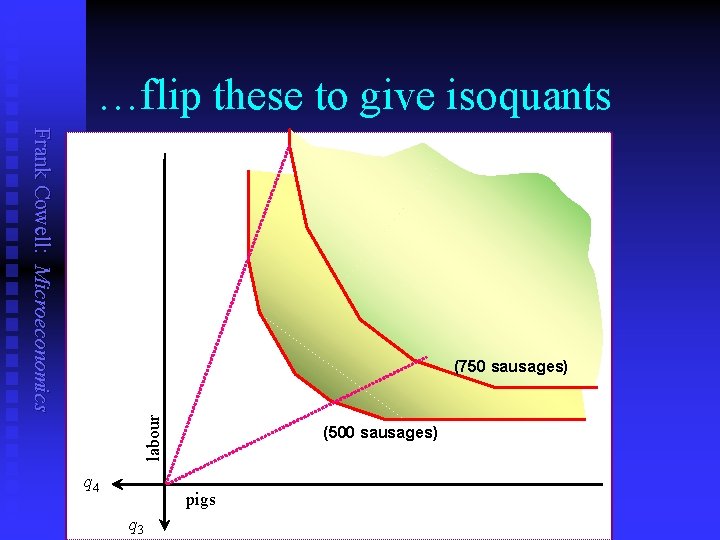
. . . to get the tradeoff in inputs pigs (500 sausages) (750 sausages) q 4 labour Frank Cowell: Microeconomics q 3

…flip these to give isoquants Frank Cowell: Microeconomics labour (750 sausages) q 4 (500 sausages) pigs q 3

A “vertical” slice through Q sausages Frank Cowell: Microeconomics Q q 1 0 pigs labour q 3 q 4

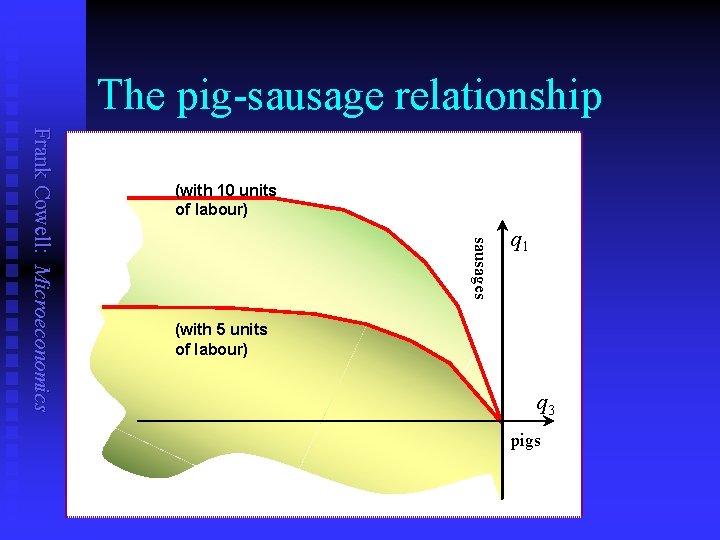
The pig-sausage relationship sausages Frank Cowell: Microeconomics (with 10 units of labour) q 1 (with 5 units of labour) q 3 pigs

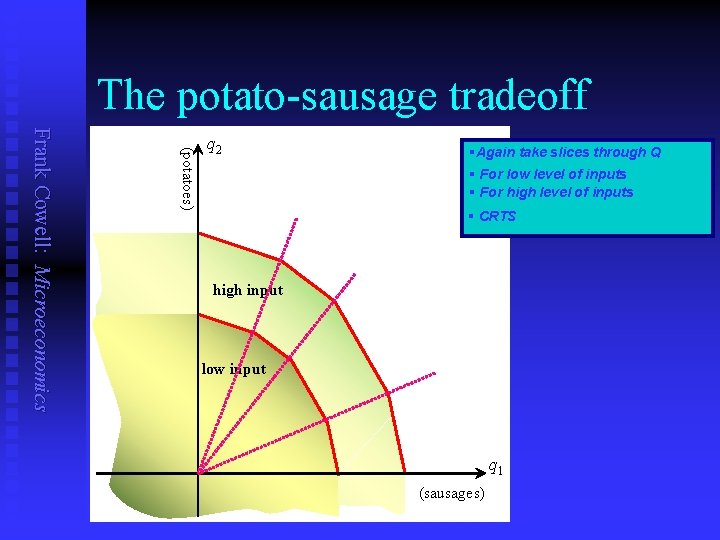
The potato-sausage tradeoff (potatoes) Frank Cowell: Microeconomics q 2 §Again take slices through Q § For low level of inputs § For high level of inputs § CRTS high input low input q 1 (sausages)

Now rework a concept we know Frank Cowell: Microeconomics Link to Firm: Basics n n n In earlier presentations we used a simple production function. A way of characterising technological feasibility in the 1 -output case. Now we have defined technological feasibility in the many-input many-output case… …using the set Q. So let’s use this to define a production function for this general case. . . …let’s see.

Frank Cowell: Microeconomics Technology set and production function n The technology set Q and the production function F are two ways of representing the same relationship: q Q Û F(q) 0 n n n Properties of F inherited from the properties with which Q is endowed. F(q 1, q 2, …, qn) is nondecreasing in each net output qi. If Q is a convex set then F is a concave function. As a convention F(q) = 0 for efficiency, so. . . F(q) 0 for feasibility.

The set Q and the function F Frank Cowell: Microeconomics §A view of the set Q: production possibilities of two outputs. q 2 F(q) > 0 §The case if Q has a smooth frontier (lots of basic techniques) § Feasible but inefficient points in the interior § Feasible and efficient points on the boundary F(q) = 0 § Infeasible points outside the boundary F(q) < 0 q 1

Frank Cowell: Microeconomics How the transformation curve is derived n n n Do this for given stocks of resources. Position of transformation curve depends on technology and resources Changing resources changes production possibilities of consumption goods

Overview. . . Frank Cowell: Microeconomics Household Demand & Supply Structure of production A simultaneous production-andconsumption problem The Robinson Crusoe problem Decentralisation Markets and trade

Setting Frank Cowell: Microeconomics n A single isolated economic agent. u u n n Owns all the resource stocks R on an island. Acts as a rational consumer. u n No market No trade (as yet) Given utility function Also acts as a producer of some of the consumption goods. u Given production function

The Crusoe problem (1) Frank Cowell: Microeconomics • max U(x) by choosing § a joint consumption and production decision x and q, subject to. . . • xÎX § logically feasible consumption • F(q) 0 § technical feasibility: equivalent to “q Î Q ” • x q+R The facts of life §materials balance: you can’t consume more of any good than is available from net output + resources We just need some reinterpretat ion

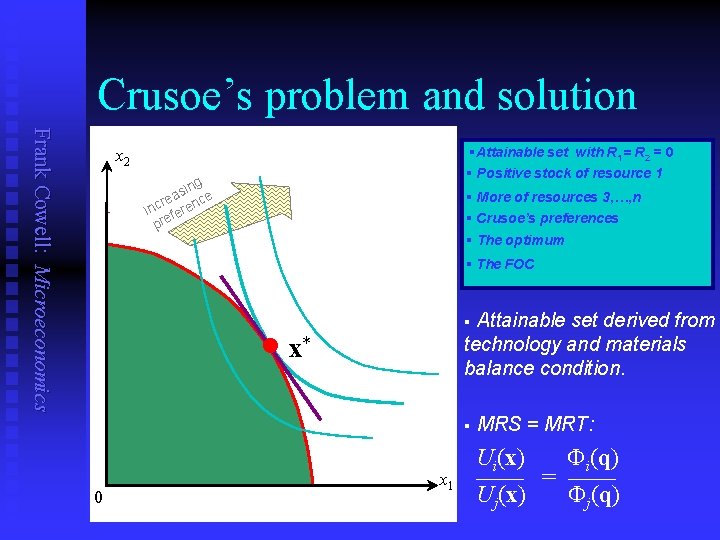
Crusoe’s problem and solution Frank Cowell: Microeconomics §Attainable set with R 1= R 2 = 0 § Positive stock of resource 1 x 2 g sin e a c re inc feren pre § More of resources 3, …, n § Crusoe’s preferences § The optimum § The FOC Attainable set derived from technology and materials balance condition. § x* § 0 x 1 MRS = MRT: Ui(x) Fi(q) —— = —— Uj(x) Fj(q)

The nature of the solution Frank Cowell: Microeconomics n From the FOC it seems as though we have two parts. . . 1. 2. n n Can these two parts be “separated out”. . . ? A story: u u u n A standard consumer optimum Something that looks like a firm's optimum Imagine that Crusoe does some accountancy in his spare time. If there were someone else on the island (“Man Friday”? ) he would delegate the production… …then use the proceeds from the production activity to maximise his utility. But to investigate this possibility we must look at the nature of income and profits

Overview. . . Frank Cowell: Microeconomics Household Demand & Supply Structure of production The role of prices in separating consumption and production decision-making The Robinson Crusoe problem Decentralisation Markets and trade

The nature of income and profits Frank Cowell: Microeconomics n n n The island is a closed and the single economic actor (Crusoe) has property rights over everything. Consists of “implicit income” from resources R and the surplus (Profit) of the production processes. We could use u u n But there is no market and therefore no prices. u n the endogenous income model of the consumer the definition of profits of the firm We may have to “invent” the prices. Examine the application to profits.

Profits and income at shadow prices Frank Cowell: Microeconomics n n n We know that there is no system of prices. Invent some “shadow prices” for accounting purposes. Use these to value national income r 1 q 1 + r 2 q 12 +. . . + rnq 1 n profits r 1 R 1 + r 2 R 2 +. . . + rn. Rn value of resource stocks r 1[q 1+R 1] +. . . + rn[qn+Rn] value of national income

National income contours Frank Cowell: Microeconomics q 2+R 2 contours for progressively higher values of national income r 1[q 1+ R 1] + r 2[q 2+ R 2 ] = const q 1+R 1

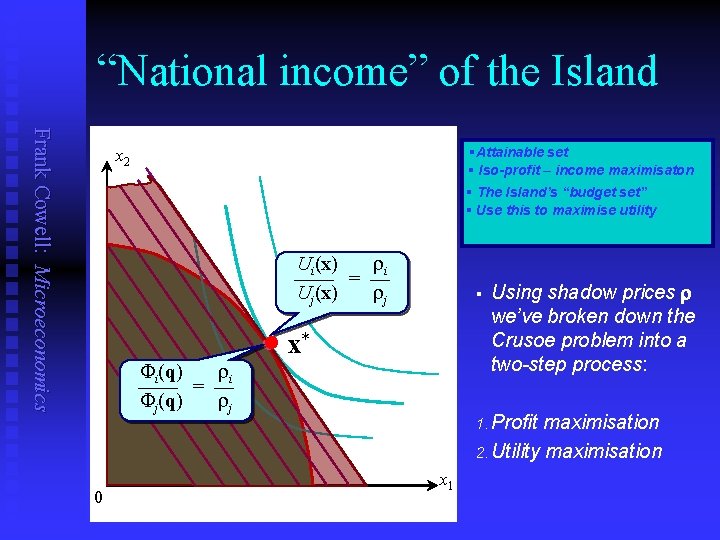
“National income” of the Island Frank Cowell: Microeconomics §Attainable set § Iso-profit – income maximisaton x 2 § The Island’s “budget set” § Use this to maximise utility Ui(x) ri —— = — Uj(x) rj Fi(q) ri —— = — Fj(q) rj 0 § x* Using shadow prices r we’ve broken down the Crusoe problem into a two-step process: 1. Profit maximisation 2. Utility maximisation x 1

A separation result Frank Cowell: Microeconomics By using “shadow prices” r … n …a global maximisation problem n …is separated into sub-problems: n 1. An income-maximisation problem. max U(x) subject to x q+R F(q) 0 max n S ri [ qi+Ri] subj. to i=1 F(q) 0 max U(x) subject to 2. A utility maximisation problem n Maximised income from 1 is used n S ri xi y i=1

The separation result Frank Cowell: Microeconomics n n n The result raises an important question. . . Can this trick always be done? It depends on the structure of the components of the problem. To see this let’s rework the Crusoe problem. Visualise it as a simultaneous valuemaximisation and value minimisation. Then see if you can spot why the separation result works. . .

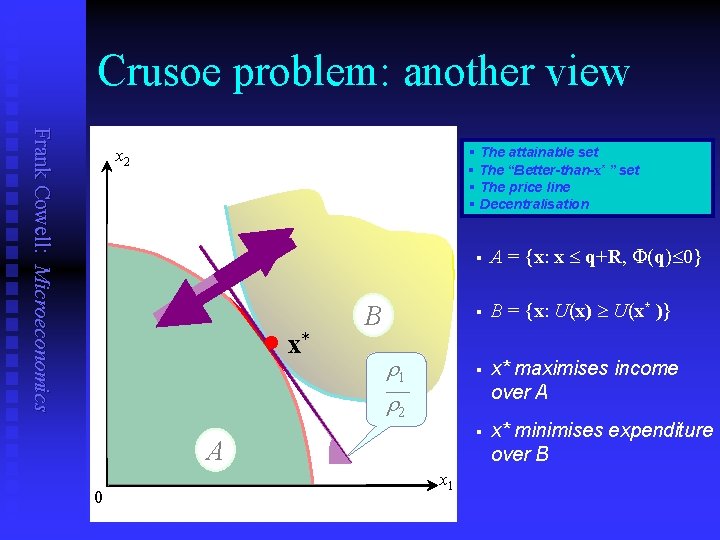
Crusoe problem: another view Frank Cowell: Microeconomics § The attainable set § The “Better-than-x* ” set § The price line § Decentralisation x 2 x* B r 1 r 2 A 0 x 1 § A = {x: x q+R, F(q) 0} § B = {x: U(x) U(x* )} § x* maximises income over A § x* minimises expenditure over B

The role of convexity Frank Cowell: Microeconomics n The “separating hyperplane” theorem is useful here. u u n n In our application: A is the Attainable set. u u n Derived from production possibilities+resources Convexity depends on divisibility of production B is the “Better-than” set. u u n Given two convex sets A and B in Rn with no points in common, you can pass a hyperplane between A and B. In R 2 a hyperplane is just a straight line. Let's look at another case. . . Derived from preference map. Convexity depends on whether people prefer mixtures. The hyperplane is the price system.

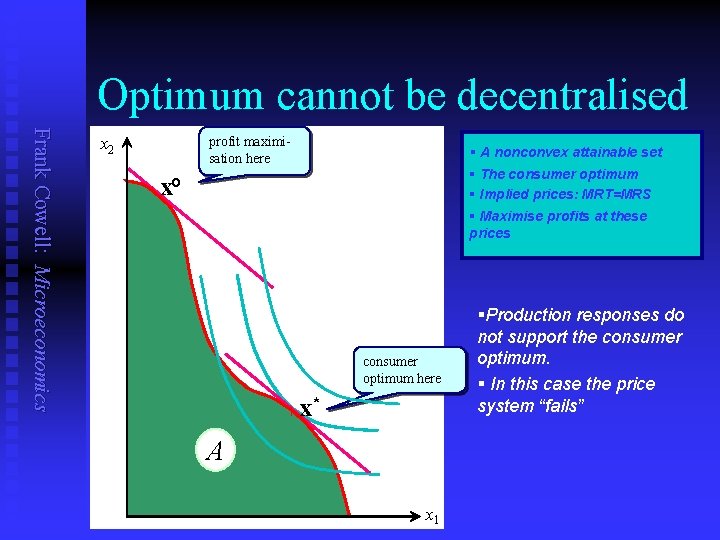
Optimum cannot be decentralised Frank Cowell: Microeconomics x 2 profit maximisation here l § A nonconvex attainable set § The consumer optimum § Implied prices: MRT=MRS x° § Maximise profits at these prices consumer optimum here l x* A x 1 §Production responses do not support the consumer optimum. § In this case the price system “fails”

Overview. . . Frank Cowell: Microeconomics Household Demand & Supply Structure of production How the market simplifies the simple model The Robinson Crusoe problem Decentralisation Markets and trade

Introducing the market again. . . Frank Cowell: Microeconomics n n n Now suppose that Crusoe has contact with the world This means that he is not restricted to “home production” He can buy/sell at world prices. This development expands the range of choice. . . and enters the separation argument in an interesting way Think again about the attainable set

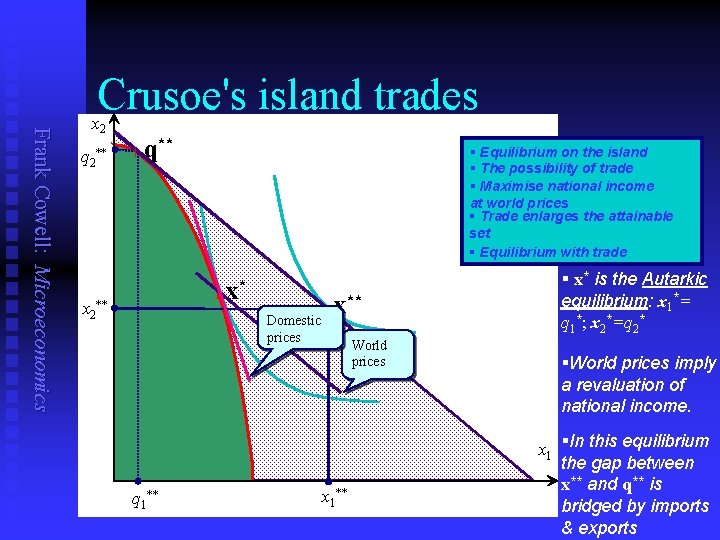
Frank Cowell: Microeconomics Crusoe's island trades x 2 q 2** x 2 l q** § Equilibrium on the island § The possibility of trade § Maximise national income at world prices § Trade enlarges the attainable set § Equilibrium with trade l ** x* Domestic prices q 1** l x** World prices x 1** § x* is the Autarkic equilibrium: x 1*= q 1*; x 2*=q 2* §World prices imply a revaluation of national income. x 1 §In this equilibrium the gap between x** and q** is bridged by imports & exports

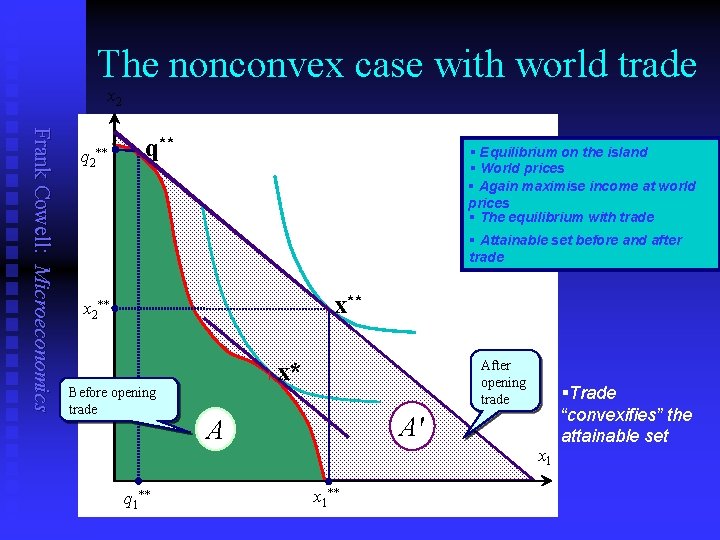
The nonconvex case with world trade x 2 Frank Cowell: Microeconomics q 2** l q** § Equilibrium on the island § World prices § Again maximise income at world prices § The equilibrium with trade § Attainable set before and after trade x 2** l l Before opening trade q 1** x* After opening trade A′ A x 1** §Trade “convexifies” the attainable set

“Convexification” Frank Cowell: Microeconomics n n There is nothing magic about this. When you write down a conventional budget set you are describing a convex set u n When you “open up” the model to trade you change u u n S pixi ≤ y, xi ≥ 0. from a world where F(·) determines the constraint to a world where a budget set determines the constraint In the new situation you can apply the separation theorem.

The Robinson Crusoe economy Frank Cowell: Microeconomics n n The global maximum is simple. But can be split up into two separate parts. u u n n n Profit (national income) maximisation. Utility maximisation. All this relies on the fundamental decentralisation result for the price system. Follows from the separating hyperplane result. “You can always separate two eggs with a single sheet of paper”