Prerequisites Almost essential Consumption and Uncertainty Probability Distributions

Prerequisites Almost essential: Consumption and Uncertainty Probability Distributions RISK MICROECONOMICS Principles and Analysis Frank Cowell April 2018 Frank Cowell : Risk 1

Risk and uncertainty § In dealing with uncertainty a lot can be done without introducing probability § Now we introduce a specific probability model • This could be some kind of exogenous mechanism • Could just involve individual’s perceptions § Facilitates discussion of risk § Introduces new way of modelling preferences April 2018 Frank Cowell : Risk 2

Probability § What type of probability model? § A number of reasonable versions: Lottery • public observable government policy? • public announced coin flip • private objective emerges from structure of • private subjective preferences § How to represent probabilities in economic models? • a few standard forms • see the presentation Probability Distributions April 2018 Frank Cowell : Risk 3

Overview Risk Shape of the u-function and attitude to risk Risk comparisons Special Cases Lotteries April 2018 Frank Cowell : Risk 4

Risk aversion and the function u § Given a probability model can discuss risk attitudes in terms of gambles § Do this in terms of properties of “felicity” or “cardinal utility” function u • Scale and origin of u are irrelevant • But the curvature of u is important § We can capture this in more than one way • we will investigate the standard approaches • then introduce two useful definitions April 2018 Frank Cowell : Risk 5

Risk aversion and choice § Imagine a simple gamble § Two payoffs with known probabilities: • x. RED with probability p. RED • x. BLUE with probability p. BLUE • Expected value Ex = p. REDx. RED + p BLUE x BLUE § A “fair gamble”: stake money is exactly Ex § Would the person accept all fair gambles? § Compare Eu(x) with u(Ex) depends on shape of u April 2018 Frank Cowell : Risk 6

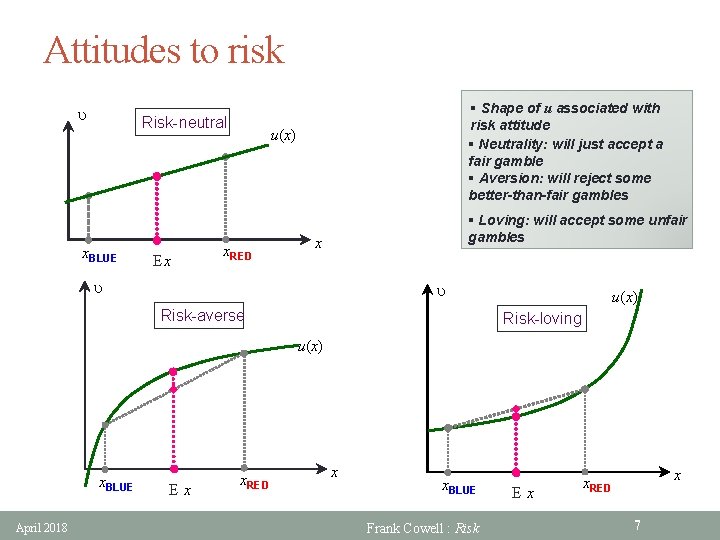
Attitudes to risk u Risk-neutral x. BLUE Ex § Shape of u associated with risk attitude § Neutrality: will just accept a fair gamble § Aversion: will reject some better-than-fair gambles u(x) x. RED § Loving: will accept some unfair gambles x u u Risk-averse u(x) Risk-loving u(x) x. BLUE April 2018 E x x. RED x x. BLUE Frank Cowell : Risk E x x x. RED 7

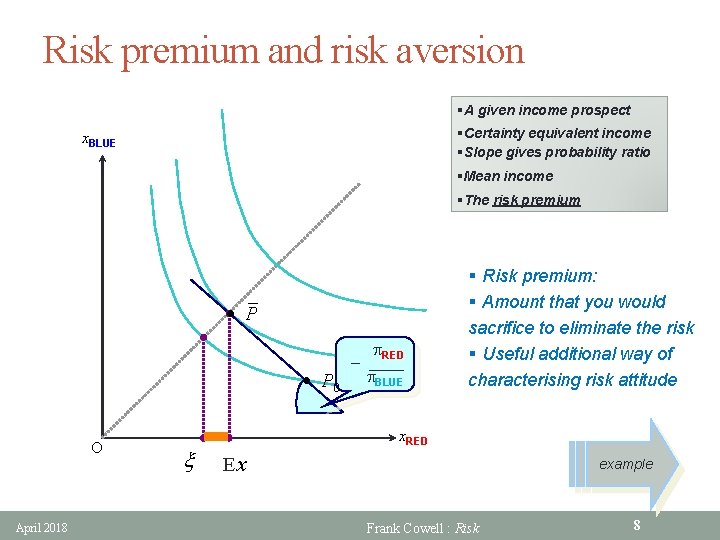
Risk premium and risk aversion §A given income prospect §Certainty equivalent income §Slope gives probability ratio x. BLUE §Mean income §The risk premium – P P 0 O April 2018 x p. RED – ____ p. BLUE § Risk premium: § Amount that you would sacrifice to eliminate the risk § Useful additional way of characterising risk attitude x. RED Ex example Frank Cowell : Risk 8

An example… § Two-state model § Subjective probabilities (0. 25, 0. 75) § Single-commodity payoff in each case April 2018 Frank Cowell : Risk 9

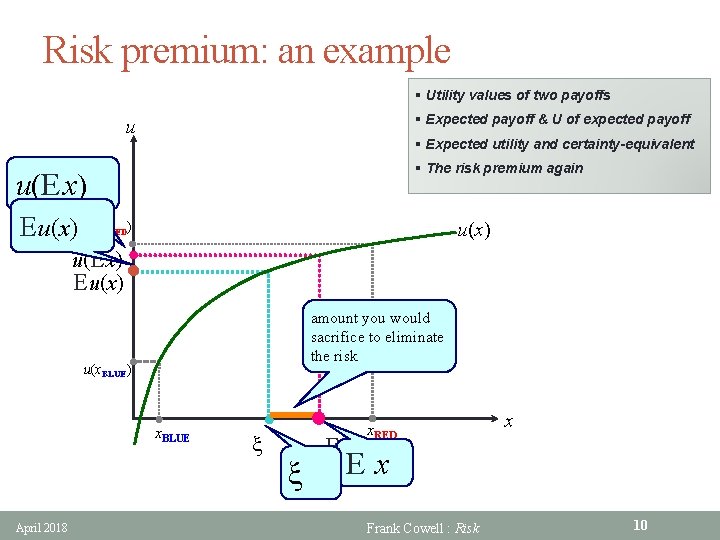
Risk premium: an example § Utility values of two payoffs § Expected payoff & U of expected payoff u § Expected utility and certainty-equivalent § The risk premium again u(E x) E u(x) u(x. RED) u(E x) E u(x) amount you would sacrifice to eliminate the risk u(x. BLUE) x. BLUE April 2018 x x Ex x. RED x E x Frank Cowell : Risk 10

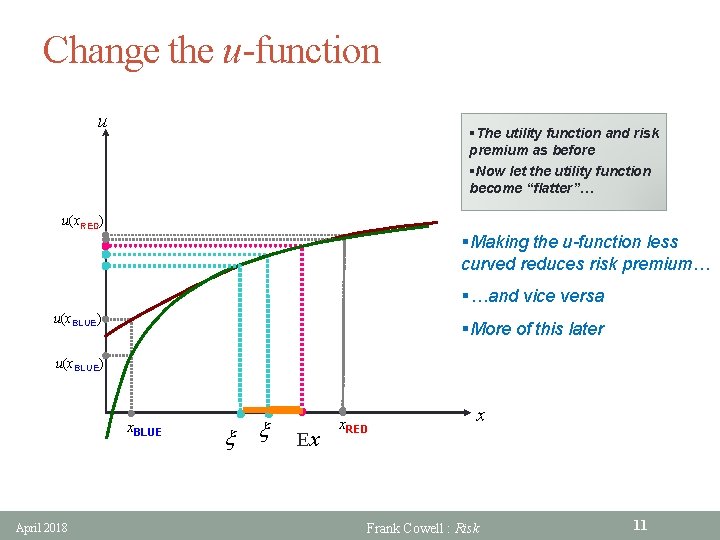
Change the u-function u §The utility function and risk premium as before §Now let the utility function become “flatter”… u(x. RED) §Making the u-function less curved reduces risk premium… §…and vice versa u(x. BLUE) §More of this later u(x. BLUE) x. BLUE April 2018 x x Ex x. RED x Frank Cowell : Risk 11

An index of risk aversion? § Risk aversion associated with shape of u • second derivative • or “curvature” § Could we summarise it in a simple index or measure? • if so, we can characterise one person as more/less risk averse than another § There is more than one way of doing this April 2018 Frank Cowell : Risk 12

Absolute risk aversion § Definition of absolute risk aversion for scalar payoffs uxx(x) a(x) : = ux(x) § For risk-averse individuals a is positive § For risk-neutral individuals a is zero § Definition ensures that a is independent of the scale and the origin of u • Multiply u by a positive constant… • …add any other constant… • a remains unchanged April 2018 Frank Cowell : Risk 13

Relative risk aversion § Definition of relative risk aversion for scalar payoffs: uxx(x) r(x) : = x ux(x) § Some basic properties of r are similar to those of a: • positive for risk-averse individuals • zero for risk-neutrality • independent of the scale and the origin of u § Obvious relation with absolute risk aversion: • r(x) = x a(x) April 2018 Frank Cowell : Risk 14

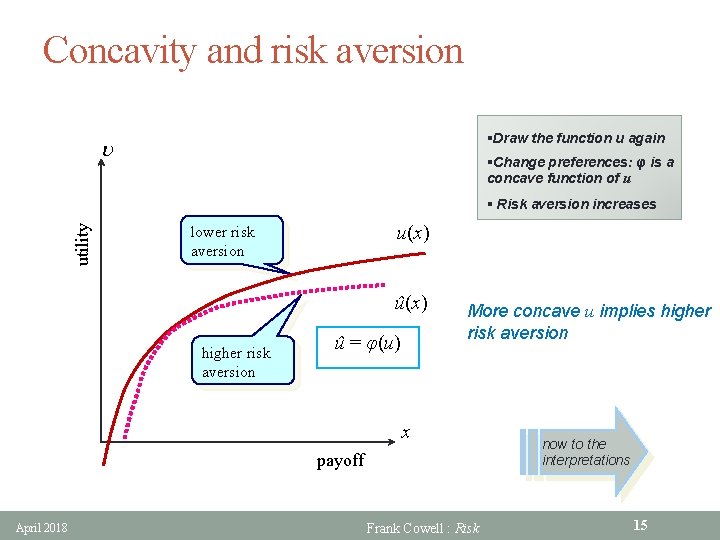
Concavity and risk aversion §Draw the function u again u §Change preferences: φ is a concave function of u utility § Risk aversion increases u(x) lower risk aversion û(x) higher risk aversion û = φ(u) More concave u implies higher risk aversion x payoff April 2018 Frank Cowell : Risk now to the interpretations 15

Interpreting a and r § Think of a as a measure of the concavity of u • Risk premium is approximately ½ a(x) var(x) § Likewise think of r as the elasticity of marginal u § In both interpretations an increase in the “curvature” of u increases measured risk aversion • suppose risk preferences change… • u is replaced by û , where û = φ(u) and φ is strictly concave • then both a(x) and r(x) increase for all x § An increase in a or r also associated with increased curvature of IC April 2018 Frank Cowell : Risk 16

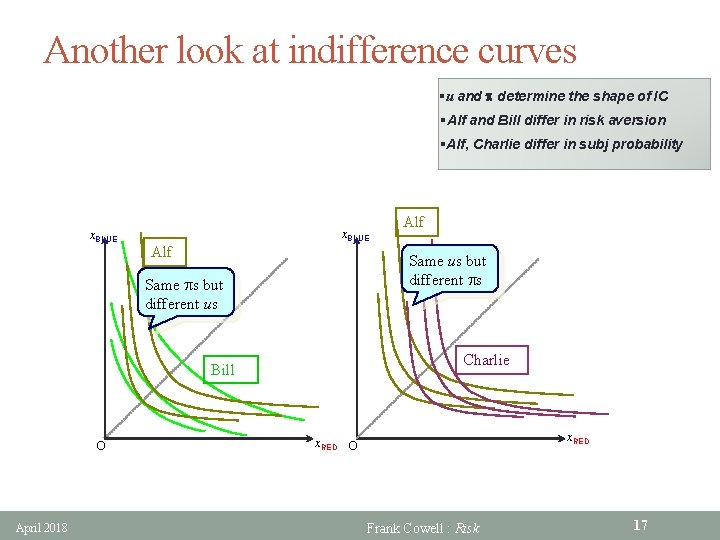
Another look at indifference curves §u and p determine the shape of IC §Alf and Bill differ in risk aversion §Alf, Charlie differ in subj probability x. BLUE Alf Same us but different ps Same ps but different us Charlie Bill O April 2018 Alf x. RED O Frank Cowell : Risk 17

Overview Risk CARA and CRRA Risk comparisons Special Cases Lotteries April 2018 Frank Cowell : Risk 18

Special utility functions? § Sometimes convenient to use special assumptions about risk • Constant ARA • Constant RRA § By definition r(x) = x a(x) § Differentiate w. r. t. x: dr(x) da(x) = a(x) + x dx dx § So one could have, for example: • constant ARA and increasing RRA • constant RRA and decreasing ARA • or, of course, decreasing ARA and increasing RRA April 2018 Frank Cowell : Risk 19

Special case 1: CARA § We take a special case of risk preferences § Assume that a(x) = a for all x § Felicity function must take the form 1 ax u(x) : = e a § Constant Absolute Risk Aversion § This induces a distinctive pattern of indifference curves… April 2018 Frank Cowell : Risk 20

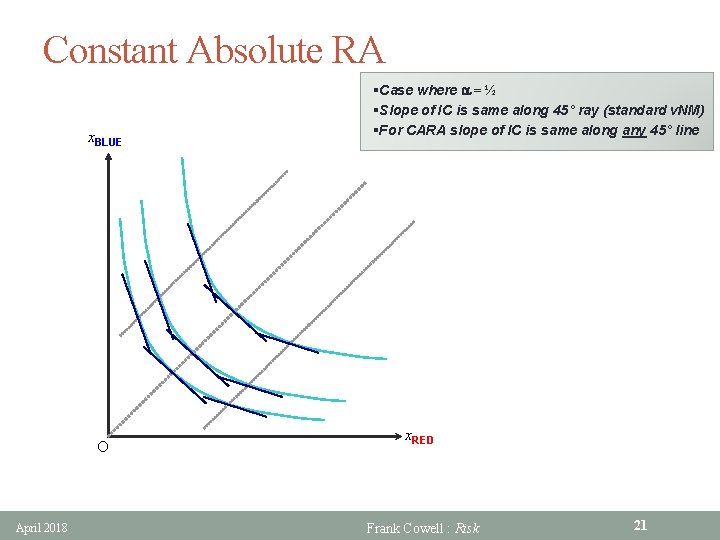
Constant Absolute RA x. BLUE O April 2018 §Case where a = ½ §Slope of IC is same along 45° ray (standard v. NM) §For CARA slope of IC is same along any 45° line x. RED Frank Cowell : Risk 21

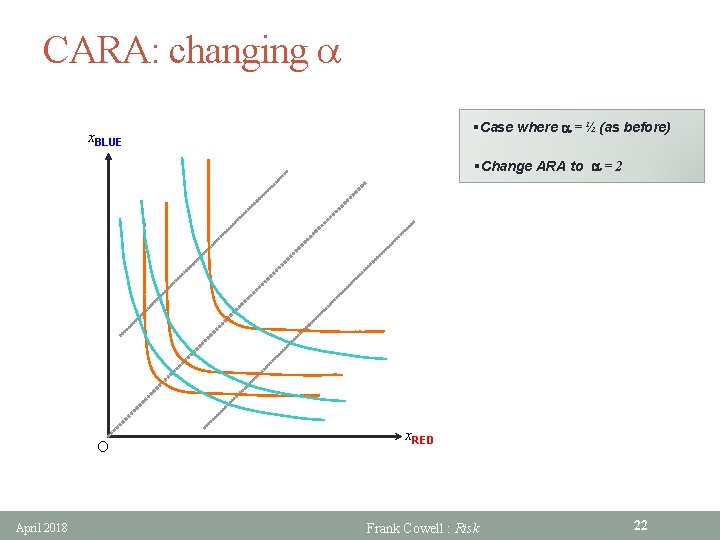
CARA: changing a §Case where a = ½ (as before) x. BLUE §Change ARA to a = 2 O April 2018 x. RED Frank Cowell : Risk 22

Special case 2: CRRA § Another important special case of risk preferences § Assume that r(x) = r for all r § Felicity function must take the form 1 1 r u(x) : = x 1 r § Constant Relative Risk Aversion § Again induces a distinctive pattern of indifference curves… April 2018 Frank Cowell : Risk 23

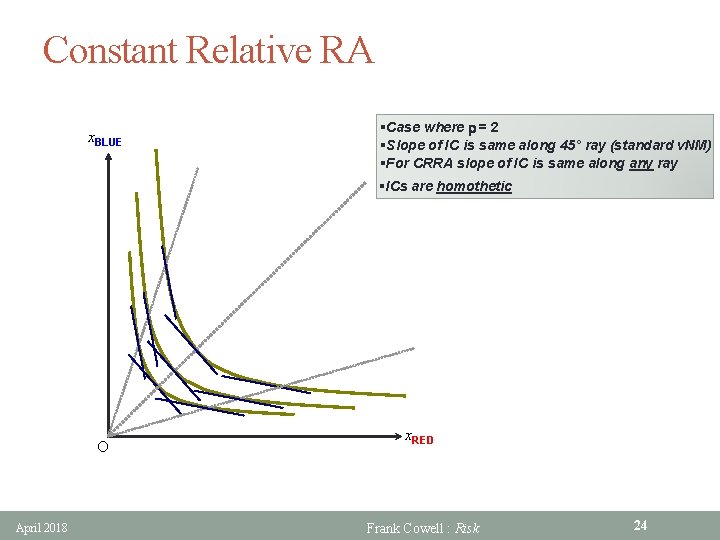
Constant Relative RA x. BLUE §Case where r = 2 §Slope of IC is same along 45° ray (standard v. NM) §For CRRA slope of IC is same along any ray §ICs are homothetic O April 2018 x. RED Frank Cowell : Risk 24

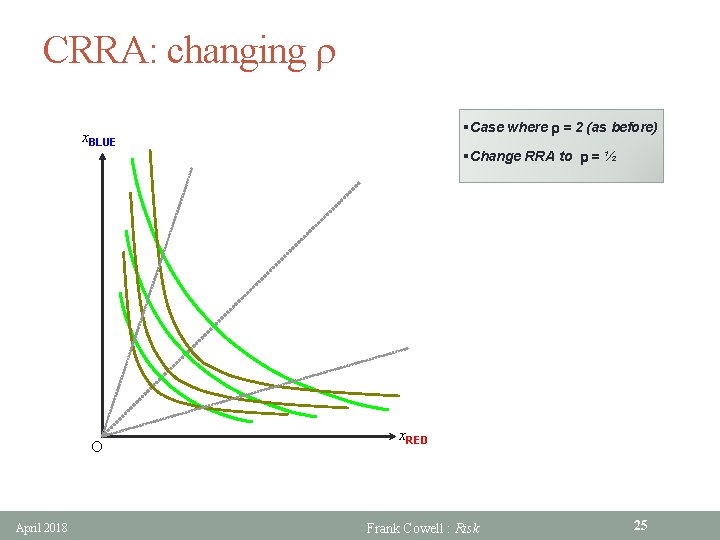
CRRA: changing r §Case where r = 2 (as before) x. BLUE O April 2018 §Change RRA to r = ½ x. RED Frank Cowell : Risk 25

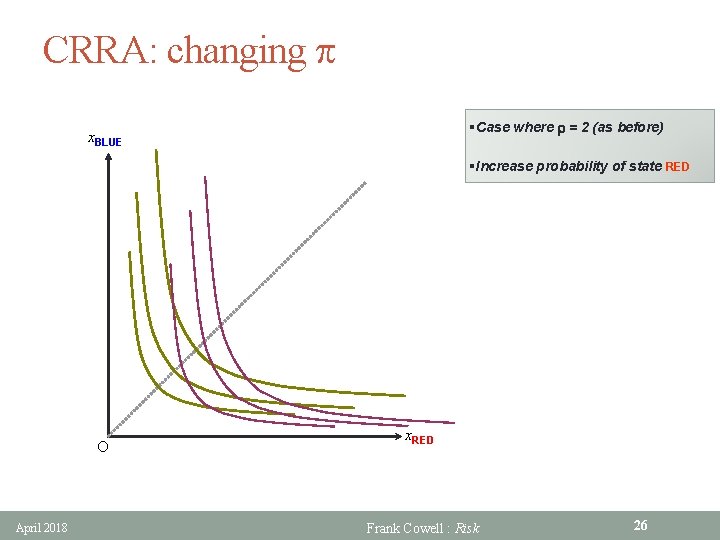
CRRA: changing p §Case where r = 2 (as before) x. BLUE §Increase probability of state RED O April 2018 x. RED Frank Cowell : Risk 26

Overview Risk Probability distributions as objects of choice Risk comparisons Special Cases Lotteries April 2018 Frank Cowell : Risk 27

Lotteries § Consider lottery as a particular type of uncertain prospect § Take an explicit probability model § Assume a finite number of states-of-the-world § Associated with each state w are: • A known payoff xw , • A known probability pw ≥ 0 § The lottery is the probability distribution over the “prizes” xw, w = 1, 2, …, • The probability distribution is just the vector p: = (p 1, , p 2 , …, , p ) • Of course, p 1+ p 2 +…+p = 1 § What about preferences? April 2018 Frank Cowell : Risk 28

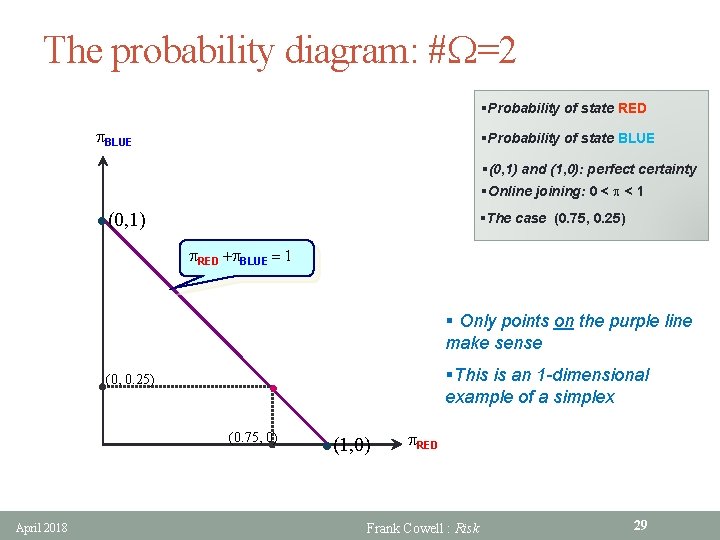
The probability diagram: #W=2 §Probability of state RED p. BLUE §Probability of state BLUE §(0, 1) and (1, 0): perfect certainty §Online joining: 0 < p < 1 l(0, 1) §The case (0. 75, 0. 25) p. RED +p. BLUE = 1 § Only points on the purple line make sense (0, 0. 25) • (0. 75, 0) April 2018 §This is an 1 -dimensional example of a simplex l(1, 0) p. RED Frank Cowell : Risk 29

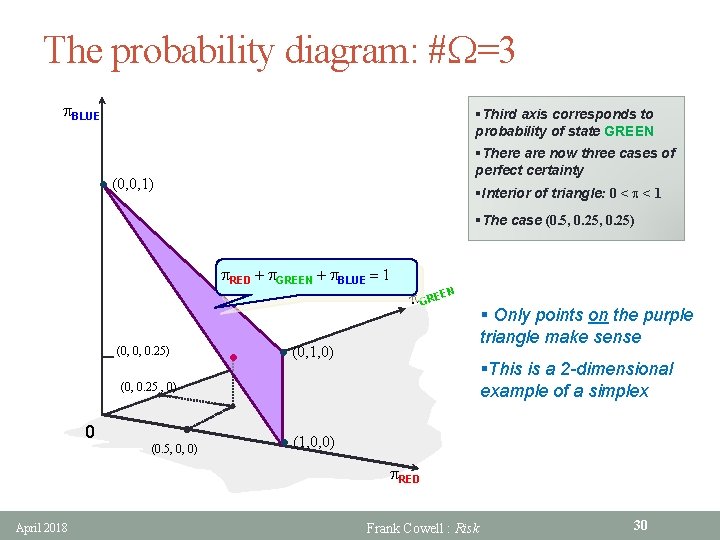
The probability diagram: #W=3 p. BLUE §Third axis corresponds to probability of state GREEN §There are now three cases of perfect certainty l (0, 0, 1) §Interior of triangle: 0 < p < 1 §The case (0. 5, 0. 25) p. RED + p. GREEN + p. BLUE = 1 N p GREE (0, 0, 0. 25) • l (0, 1, 0) §This is a 2 -dimensional example of a simplex (0, 0. 25 , 0) 0 (0. 5, 0, 0) § Only points on the purple triangle make sense l (1, 0, 0) p. RED April 2018 Frank Cowell : Risk 30

Probability diagram #W=3 (contd. ) l (0, 0, 1) §All the essential information is in the simplex §Display as a plane diagram §The equi-probable case §The case (0. 5, 0. 25) • • l . (1, 0, 0) April 2018 (1/3, 1/3) (0. 5, 0. 25) l (0, 1, 0) Frank Cowell : Risk 31

Preferences over lotteries § Take the probability distributions as objects of choice § Imagine a set of lotteries p°, p', p", … § Each lottery p has same payoff structure • state-of-the-world w has payoff xw • w has probability pw° or pw' or pw" …. , depending on which lottery § We need an alternative axiomatisation for choice amongst lotteries p April 2018 Frank Cowell : Risk 32

Axioms on preferences § April 2018 Frank Cowell : Risk 33

Basic result § Take the axioms transitivity, independence, continuity § Imply that preferences must be representable in the form of a von Neumann-Morgenstern utility function: å pw u(xw) w ÎW § or equivalently: å pw uw w ÎW where uw : = u(xw) § So we can also see the EU model as a weighted sum of ps April 2018 Frank Cowell : Risk 34

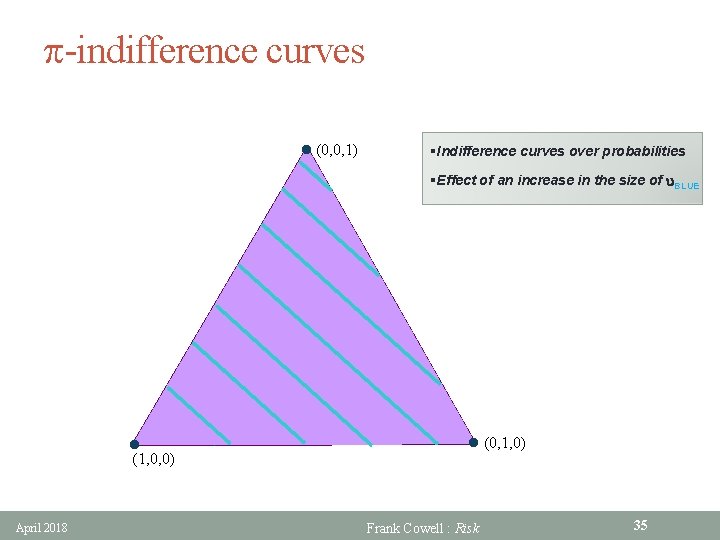
p-indifference curves l (0, 0, 1) §Indifference curves over probabilities §Effect of an increase in the size of u. BLUE l . (1, 0, 0) April 2018 l (0, 1, 0) Frank Cowell : Risk 35

What next? § Simple trading model under uncertainty § Consumer choice under uncertainty § Models of asset holding § Models of insurance § This is in the presentation Risk Taking April 2018 Frank Cowell : Risk 36