Prerequisites Almost essential Games Mixed Strategies Frank Cowell

Prerequisites Almost essential Games: Mixed Strategies Frank Cowell: Microeconomics February 2007 Games: Uncertainty MICROECONOMICS Principles and Analysis Frank Cowell

Overview. . . Games: Uncertainty Frank Cowell: Microeconomics Basic structure Introduction to the issues… A model Illustration

Introduction Frank Cowell: Microeconomics n A logical move forward in strategic analysis u u n Important development u u n follows naturally from considering role of time similar issues arise concerning the specification of payoffs lays the basis for the economics of information concerns the way in which uncertainty is treated Connections with analysis of risk-taking u u make use of expected utility analysis but introduce some innovative thinking….

Uncertainty Frank Cowell: Microeconomics n Distinguish from simple randomisation u u n Incomplete information u u n decisions made before features of the game are known yet players act rationally Alternative perspective on uncertainty: u u n in principle it is distinct from idea of “mixed strategy”… …but see solution method later an additional player “nature” makes a move Role of uncertainty u u u principally concerns types of player may know distribution of types… …but not the type of any one individual agent

Types Frank Cowell: Microeconomics n Type concerns the nature of each agent u u n Can think of type in terms of “identity” u u n same agent can take on a number of identities example t two actual persons – Alf and Bill t two types – good-cop, bad-cop t four identities – Alf-good, Alf-bad, Bill-good, Bill-bad Type affects nature of strategic choices u n people’s tastes and behaviour may differ according to (unobserved) health status firms’ costs and behaviour may differ according to (unobserved) efficiency which agent is which type? Type affects outcomes u payoffs that players get from individual outcomes of the game

Objectives and payoffs Frank Cowell: Microeconomics n Agents’ objectives u u u n Payoffs? u n u taken over joint distribution of types… …conditional on one’s own type Probabilities? u u n cardinal payoffs in each possible outcome of the game Expectation? u n given the “uncertainty” setting… …makes sense to use expected utility but specified how? determined by nature? chosen by players? Need to look at a specific model to see how this works

Overview. . . Games: Uncertainty Frank Cowell: Microeconomics Basic structure principles for incorporating uncertainty A model Illustration

Types Frank Cowell: Microeconomics n n n Begin with the focus of the incomplete information: types Assume that the types of agent h is a number th Î [0, 1] Can cover a wide range of individual characteristics Example where each h is either type [healthy] or type [ill] h u let [healthy] be denoted t = 0 u let [ill] be denoted th = 0 u suppose π is the probability agent h is healthy u joint probability distribution over health types: p if 0 ≤ th <1 u F(th | [t] h) = 1 if t h =1 Now consider the decision problem…

Payoffs and types Frank Cowell: Microeconomics n An agent’s type may affect his payoffs u n n if I become ill I may get lower level of utility from a given consumption bundle than if I stay healthy We need to modify the notation to allow for this. Agent h’s utility is Vh(sh, [s] h ; τh) u u u sh : h's strategy [s] h : everybody else's strategy τh : the type associated with player h

Beliefs, probabilities and payoffs (1) Frank Cowell: Microeconomics n n Agent h does not know types of the other agents But may have a set of beliefs about them u n n will select a strategy based on these beliefs Beliefs incorporated into a probabilistic model Represented by a distribution function F u u joint probability distribution of types t over the agents assumed to be common knowledge

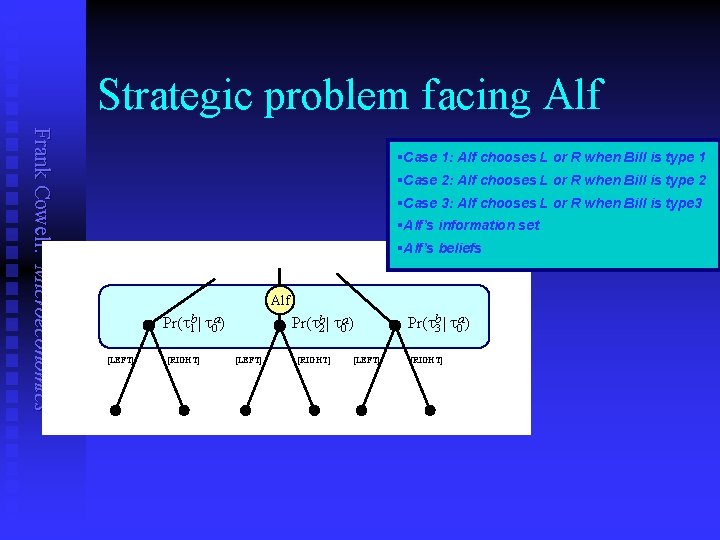
Beliefs, probabilities and payoffs (2) Frank Cowell: Microeconomics n n n An example to illustrate Suppose Alf is revealed to be of type t 0 a u is about to choose [LEFT] or [RIGHT], u but doesn’t know Bill's type at the moment of this decision. Suppose there are 3 possibilities in Alf’s information set u n n Alf knows the distribution of types that Bill may possess Can rationally assign conditional probabilities u u n t 1 b, t 2 b , t 3 b conditional on type that has been realised for Alf Pr(t 1 b | t 0 a), Pr(t 2 b | t 0 a) and Pr(t 3 b | t 0 a) These are Alf's beliefs about Bill’s type

Strategic problem facing Alf Frank Cowell: Microeconomics §Case 1: Alf chooses L or R when Bill is type 1 §Case 2: Alf chooses L or R when Bill is type 2 §Case 3: Alf chooses L or R when Bill is type 3 §Alf’s information set §Alf’s beliefs Alf Pr(t 1 b| t 0 a) [LEFT] [RIGHT] Pr(t 2 b | t 0 a) [LEFT] [RIGHT] [LEFT] Pr(t 3 b | t 0 a) [RIGHT]

Strategies again Frank Cowell: Microeconomics n “Games: mixed” Recall an interpretation of pure strategies u u n Now we have a more complex issue to consider u u n the appropriate strategy for h may depend on h’s type th so a strategy is no longer a single “button” Each agent’s strategy is conditioned on his type u u u n like “radio buttons” push one and only one of the buttons strategy is a “button rule” a function h(⋅) from set of types to set of pure strategies Sh specifies a particular button for each possible value of the type th Example: u u u agent h can be of exactly one of two types: th Î {[healthy], [ill]} agent h’s button rule h(⋅) will generate one of two pure strategies s 0 h = h([healthy]) or s 1 h = h([ill]) according to the value of th realised at the beginning of the game

Conditional strategies and utility Frank Cowell: Microeconomics n Rule for agent h : u u u n Likewise for all agents other than h u n [s] h = [ 1 (t 1 ), . . . , h 1 (th 1 ), h+1 (th+1 ), …] Agent h’s utility is determined by… u u n once agent h’s type is determined then… h’s button rule h(⋅)… generates a strategy sh = h(th) everyone’s strategies and h’s type: Vh(sh, [s] h ; τh) equivalently : Vh( 1(t 1), 2(t 2), . . . ; th) But others’ types unknown at time of h’s decision u u u Use the notation E(∙| th ) to denote conditional expectation over h’s beliefs about others’ types given his own type so criterion is expected utility : E(Vh(sh, [s] h| th))

Describing the game (1) Frank Cowell: Microeconomics n n n Certainty case analysed previously Objective is utility: vh(sh, [s] h) Game is characterised by two objects u u n n n [v 1, v 2, . . . ] [S 1, S 2, . . . ] a profile of utility functions list of strategy sets Game under uncertainty analysed here Objective is expected utility: E(Vh (sh , [s] h | th )) Game is characterised by three objects u u u [V 1 , V 2 , . . . ] [S 1 , S 2 , . . . ] F (⋅) a profile of utility functions, list of strategy sets joint probability distribution of types (beliefs)

Describing the game (2) Frank Cowell: Microeconomics n n Can recast the game in a familiar way Take each agent’s “button-rule” h(⋅) as a redefined strategy in its own right u u u n Let Sh be the set of redefined strategies (“button rules”) u then the game [V 1, V 2, . . . ] [S 1, S 2, . . . ] F (⋅) u n agent h gets utility vh( h, [ ] h) …equals E(Vh (sh , [s] h | th )) …where vh is as in certainty game is equivalent to the game [v 1, v 2, . . . ], [S 1, S 2, . . . ] A standard game with redefined strategy sets for each player

Equilibrium Frank Cowell: Microeconomics n Re-examine meaning of equilibrium u u n n Alternative representation of the game neatly introduces the idea of equilibrium A pure strategy Bayesian Nash equilibrium consists of u u n a refinement… …allows for the type of uncertainty that we have just modelled. a profile of rules [ *(⋅)] … …that is a NE of the game [v 1, v 2, . . . ], [S 1, S 2, . . . ] Means that we can just adapt standard NE definition u u u replace the ordinary strategies (“buttons”) in the NE with the conditional strategies “button rules” *h(⋅) where *h (⋅) Î argmax vh ( h (⋅), [ * (⋅)] h )

Equilibrium: definition Frank Cowell: Microeconomics n Definition u u u n A profile of decision rules [ *] is a Bayesian-Nash equilibrium for the game… … if and only if for all h and for any t 0 h occurring with positive probability E(Vh( *h(t 0 h), [s*] h| t 0 h)) ≥ E(Vh(sh, [s*] h| t 0 h)) for all sh Î Sh Identity interpretation u u Bayesian equilibrium as a Nash equilibrium of a game with a larger number of players if there are n players and m types this setup as equivalent to a game with mn players Each agent in a particular identity plays to maximise expected utility in that identity

Model: summary Frank Cowell: Microeconomics n We have extended the standard analysis u u u n To allow for case where agents’ types are unknown u u n objectives strategies equilibrium everything based on expected values… … conditioned on agent’s own type Let’s put this to work in an example u u illustrate equilibrium concept outline a method of solution

Overview. . . Games: Uncertainty Frank Cowell: Microeconomics Basic structure the entry game (again) A model Illustration

Entry game: uncertainty Frank Cowell: Microeconomics n n Connected to previous lectures of strategic issues in industrial organisation But there’s a new twist u u n Firm 1 can commit to investment u u n characteristics of firm 1 (the incumbent) … …not fully known by firm 2 (an entrant) would enhance firm 1's market position might deter entry Cost of investment is crucial u u Begin with a review of the certainty case firm 1 may be either high cost or low cost which of these two actually applies is unknown to firm 2

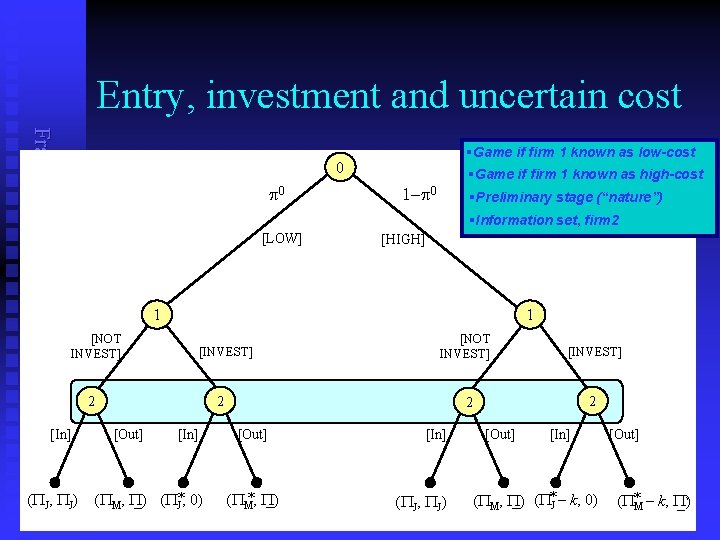
Entry and investment: certainty Frank Cowell: Microeconomics §If firm 1 has not invested… 1 §Firm 2 makes choice about entry [NOT INVEST] [INVEST] 2 [In] §If firm 1 has invested… §Firm 2 makes choice about entry 2 [Out] [In] (PJ, PJ) (PM, P) _ (P*J, 0) §Payoffs [Out] §Payoffs (PM*, P) _ §If firm 2 stays out, it makes reservation profits P > 0 §So, if firm 1 chooses [INVEST], firm 2 will choose [out] §If firm 1 chooses [NOT INVEST], both firms get PJ §So, if PM* > PJ firm 1 will choose [INVEST] Now introduce uncertainty about firm 1’s costs

Entry under uncertainty: timing Frank Cowell: Microeconomics n First a preliminary move by “Nature” (player 0) u u n Then a simultaneous moves by firms u u n firm 1, chooses whether or not to invest firm 2, chooses whether or not to enter Analyse by breaking down problem u u n that determines firm 1’s cost type unobserved by firm 2 by firm 1's circumstances… …and by behaviour Consider the following three cases…

Entry under uncertainty: case 1 Frank Cowell: Microeconomics n n Start with the very easy part of the model If Firm 1 does not invest: u u n Then if firm 2 enters: u u n there is no problem about “type” we’re back in the model of entry under certainty a joint-profit solution both firms get payoff PJ But if firm 2 stays out u u u firm 2 makes reservation profits P where 0 < PJ firm 1 makes monopoly profits PM

Entry under uncertainty: cases 2, 3 Frank Cowell: Microeconomics n n [2] If Firm 1 invests and is low cost: Then if firm 2 enters u u n But if firm 2 stays out u u n n firm 1 gets enhanced monopoly profits PM* > PM firm 2 gets reservation profits P [3] If Firm 1 invests and is high cost: Then if firm 2 enters u u n firm 1 makes profits PJ* < PJ firm 2's profits are forced to zero firm 1 makes profits PJ* − k (where k > 0) firm 2's profits are forced to zero But if firm 2 stays out u u firm 1 gets enhanced monopoly profits PM* − k firm 2 gets reservation profits P Now assemble all this in a diagram

Entry, investment and uncertain cost Frank Cowell: Microeconomics §Game if firm 1 known as low-cost 0 p 0 §Game if firm 1 known as high-cost 1 p 0 §Preliminary stage (“nature”) §Information set, firm 2 [LOW] [HIGH] 1 [NOT INVEST] [In] 1 [INVEST] 2 [NOT INVEST] [INVEST] 2 2 2 [Out] [In] (PJ, PJ) (PM, P) _ (P*J, 0) [Out] (PM*, P) _ [In] (PJ, PJ) [Out] [In] _ (P*J – k, 0) (PM, P) [Out] (P*M – k, P) _`

The role of cost Frank Cowell: Microeconomics n n n Outcome depends on k What is the potential advantage to firm 1 of investing? Assuming firm 1 is low cost: u u n Assuming firm 1 is high cost: u u n n if firm 2 enters: PJ* − k − PJ if does not enter: PM* − k − PM To make the model interesting assume that k is large u n if firm 2 enters: PJ* − PJ if does not enter: PM* − PM k > max {PJ* − PJ, PM* − PM} Then it’s never optimal for firm 1 to invest if it is high cost But what’s the equilibrium…?

Equilibrium: methodology Frank Cowell: Microeconomics n To find equilibrium, use “artificial uncertainty” as a device: u u u n So define the following probabilities: u u u n p 0: Pr that “Nature” endows firm 1 with low cost p 1 : Pr that firm 1 chooses [INVEST] given that its cost is low π² : Pr that firm 2 chooses [In]. Nature of the following probabilities: u u n although we focus on pure strategies… …it’s useful to consider a randomisation by the firms i = 1, 2 i plays each of the two moves it can take with probability (pi, 1−pi) p 0: exogenous and common knowledge. p 1, π² : chosen optimally firms A pure-strategy equilibrium is one where u u p 1 is either 0 or 1 and π² is either 0 or 1

Firm 1’s expected profits Frank Cowell: Microeconomics n Consider expected P 1 conditional on investment decision: u u u n Therefore we compute expected profits as u n EP¹= K +[K* − K] p 0 p 1 So expected profits increase with p 1 if K* > K u u n EP 1 = p 0 [p 1 K* +[1 − p 1 ]K] + [1 − p 0 ]K Simplifying this we get u n if 1 does not invest: K : = p 2 PJ +[1 − p 2] PM if 1 invests and is low cost: K* : = p 2 PJ* +[1 − p 2] PM* if 1 invests and is high cost: [not relevant, by assumption] this condition is equivalent to requiring p 2 <1 / [1 + g] …where g : = [PJ* − PJ] / [PM* − PM] Likewise expected profits decrease with p 1 if K* > K u the case where p 2 > 1 / [1 + g]

Firm 2’s expected profits Frank Cowell: Microeconomics n Consider expected P 2 conditional on investment decision: u if 1 does not invest: H : = p 2 PJ +[1 − p 2] P u if 1 invests and is low cost: H* : = [1 − p 2] P u n n Therefore we compute expected profits as u EP 2 = p 0[p 1 H* +[1 − p 1]H] + [1 − p 0]H Simplifying this we get u u n if 1 invests and is high cost: [not relevant, by assumption] EP 2 = H + [H* − H] p 0 p 1 E P 2 = P + p 2 [P J − P − p 0 p 1 P J ] So expected profits increase with p 2 if PJ − P u p 1 < ──── p 0 PJ

An equilibrium Frank Cowell: Microeconomics n n Work back from the last stage Firm 2’s decision: u u u n Firm 1’s decision: u decrease p 1 to its min value (p 1 = 0)… …as long as p 2 > 1 / [1+g] u this condition obviously holds if p 2 = 1 in the final stage u n So there is a NE such that u u n increase p 2 up to its max value (p 2 = 1)… …as long as p 1 < [PJ − P] / [p 0 PJ] if firm 1 has set p 1 = 0 then clearly this condition holds “p 2 = 1” is the best response to “p 1 = 0” is the best response to “p 2 = 1” In this NE u u p 1 = 0 means firm 1 chooses [NOT INVEST] p 2 = 1 means firm 2 chooses [In]

Another equilibrium? Frank Cowell: Microeconomics n n Again work back from the last stage Firm 2’s decision: u u u n Firm 1’s decision: u increase p 1 up to its max value (p 1 = 1)… …as long as p 2 < 1 / [1+g] u this condition obviously holds if p 2 = 0 in the final stage u n So if p 0 is large enough there is a NE such that u u n decrease p 2 up to its min value (p 2 = 0)… …as long as p 1 > [PJ − P] / [p 0 PJ] this condition can only hold if p 0 is “large enough”: p 0 ≥ 1 P/PJ “p 2 = 0” is the best response to “p 1 = 1” is the best response to “p 2 = 0” In this NE u u p 1 = 1 means firm 1 chooses [INVEST] p 2 = 01 means firm 2 chooses [Out]

The entry game: summary Frank Cowell: Microeconomics n Method similar to many simple games u u n n But there may be multiple equilibria We find one or two NEs in pure strategies u u n simultaneous moves… find mixed-strategy equilibrium [NOT INVEST] [In] – always an equilibrium [INVEST] [Out] – equilibrium if firm 1 is likely to be low-cost There may also be a mixed-strategy u if firm 1 is likely to be low-cost

Summary Frank Cowell: Microeconomics n New concepts u u n Method u u u n Nature as a player Bayesian-Nash equilibrium visualise agents of different types as though they were different agents extend computation of NE… …to maximisation of expected payoff What next? u u Economics of Information See presentation on Adverse selection