Homomorphic Encryption over Polynomial Rings Craig Gentry and

Homomorphic Encryption over Polynomial Rings Craig Gentry and Shai Halevi June 4, 2014 China Summer School on Lattices and Cryptography

The Ring LWE Problem (RLWE)

Recall LWE (traditional formulation): Hard to distinguish between (A, b = As+e) and (A, b = uniform). LWE (alternative formulation): Hard to distinguish whether matrix B = (b, A) is uniform, or there exists a vector t = (1, -s) such that e = B·t is short. Matrices and vectors are over the ring Zq. What if we put the matrices and vectors over a different ring – e. g. , a polynomial ring?

Polynomial Rings Example: Zq[x]/(x. N-1) – polynomials of degree N-1 (which have N coefficients) over Zq. Addition: Add the polynomials modulo q. Multiplication: Multiply the 2 polynomials, reduce the result modulo q and modulo x. N-1, so that the final result has degree at most N-1 again. a(x)b(x) = Σ aj· bk · xj+k mod N. Example: Zq[x]/ФN(x) – polynomials modulo q and the N-th cyclotomic polynomial E. g. , ФN(x) = (x. N/2+1) when N is a power of 2

RLWE: LWE over Polynomial Rings

Pros and Cons of RLWE (vs LWE) Con: Security LWE is as hard on average as worst-case problems over general (any) lattices RLWE is as hard on average as worst-case problems over ideal lattices (a special type of lattice) Pro: Efficiency Fast Fourier Transform (FFT): multiplying ring elements is fast even if ring has high dimension Takes O(n log n) time for rings of dimension n Also, RLWE permits smaller public keys, larger plaintexts, and more efficient homomorphic computation.

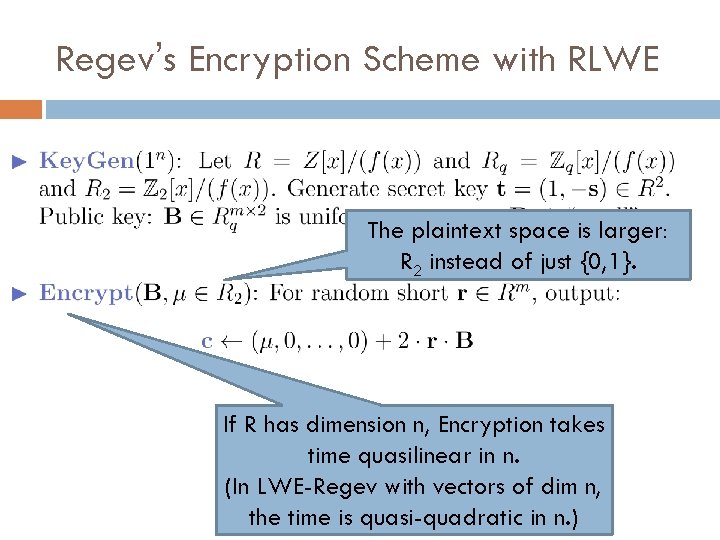
Regev’s Encryption Scheme with RLWE In LWE-Regev, m = O(n log q). For RLWE-Regev, m = O(log q).

Regev’s Encryption Scheme with RLWE The plaintext space is larger: R 2 instead of just {0, 1}. If R has dimension n, Encryption takes time quasilinear in n. (In LWE-Regev with vectors of dim n, the time is quasi-quadratic in n. )

Regev’s Encryption Scheme with RLWE

The NTRU Encryption Scheme

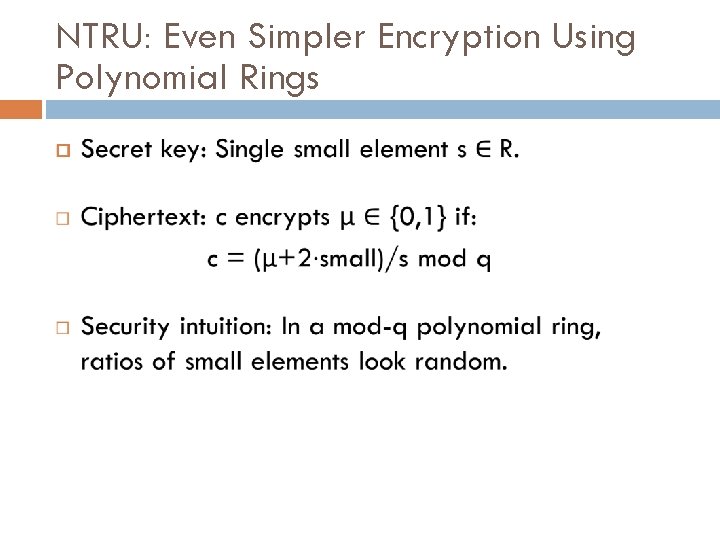
NTRU: Even Simpler Encryption Using Polynomial Rings

NTRU Details

NTRU Homomorphic Operations

Key Switching from s 1 to s 2.

Homomorphic Computation on Encrypted Arrays (SIMD Operations)

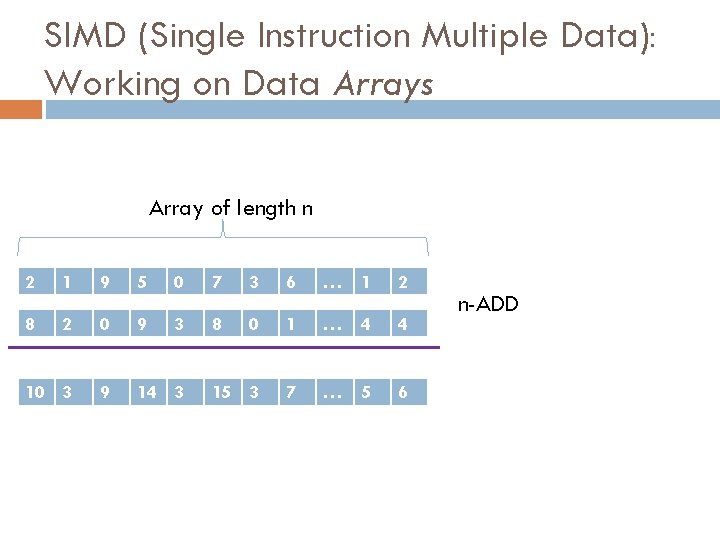
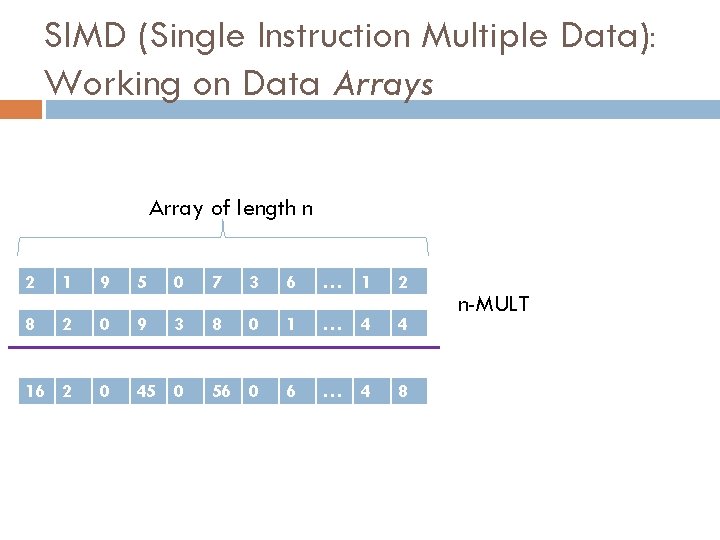
Encrypted Arrays Suppose we use a mod-15 plaintext space (not mod-2) Z 15 = Z 3 × Z 5. Chinese Remainder Theorem (CRT). From one “big” plaintext space we get 2 independent “small” plaintext spaces. We call them two “plaintext slots”. Suppose two ciphertexts c and c’ have (r 3, r 5) and (r 3’, r 5’) in their respective mod-3 and mod-5 “plaintext slots” = ADD(c, c’) has (r 3+r 3’, r 5+r 5’) in its slots. c. MULT = MULT(c, c’) has (r 3∙r 3’, r 5∙r 5’) in its slots. Homomorphic ops act component-wise, in parallel, on slots. c. ADD

Our Weird Cyclotomic Plaintext Space SWHE in Polynomial Rings Plaintext space is R 2 = Z 2[x]/ФN(x). message μ(x) is a polynomial in R 2. μ has n bits, where n is the degree of ФN(x). NTRU example: μ = [[c·s]q]2 over the ring R. The Can we get many “plaintext slots” out of R 2? Sure…

Our Weird Cyclotomic Plaintext Space The plaintext space R 2 = Z 2[x]/ФN(x) has amazing properties! Much better than a mod-15 plaintext space! Via CRT, R 2 decomposes into about N/log(N) plaintext slots of about log(N) bits apiece (for well-chosen N). Via ring automorphisms, encrypted data can be moved between slots. ADD and MULT work in parallel across the slots. We have ADD, MULT, and PERMUTE. Can evaluate boolean circuits with ciphertexts “packed”. Reduces overhead.

Chinese Remainder Theorem for Cyclotomic Rings Choose N so that ФN(x) factors mod 2 into t factors. Chinese Remainder Theorem (CRT) – polynomial version ФN(x) = fi(x) mod 2. Degrees of f 1, …, ft are d=φ(N)/t. Z 2[x]/ФN(x) = Z 2[x]/f 1(x) × … × Z 2[x]/ft(x) If ciphertexts c and c’ have (r 1(x), …, rt(x)) and (r 1’(x), …, rt’(x)) in their respective plaintext slots c. ADD = ADD(c, c’) has (r 1(x)+r 1’(x), c. MULT = MULT(c, c’) has (r 1(x)∙r 1’(x) …, rt(x)+rt’(x)). mod f 1(x), …, rt(x)∙rt’(x) mod ft(x)). Homomorphic ops act component-wise, in parallel, on slots.

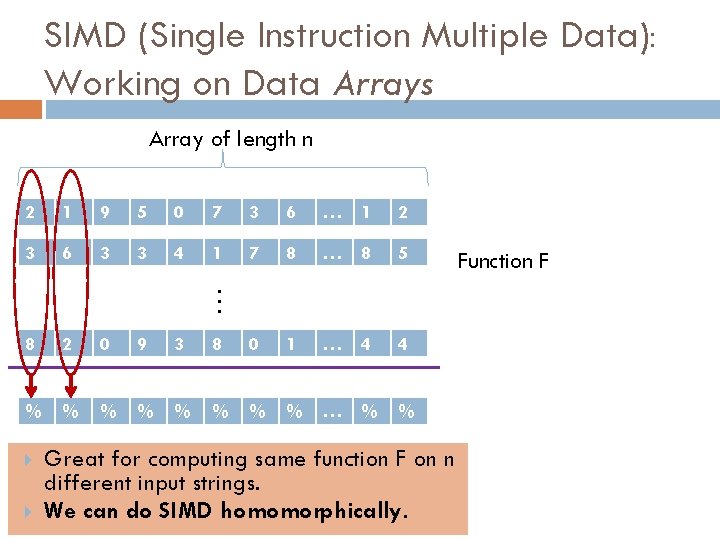
SIMD (Single Instruction Multiple Data): Working on Data Arrays Array of length n 2 1 9 5 0 7 3 6 … 1 2 8 2 0 9 3 8 0 1 … 4 4 10 3 9 14 3 15 3 7 … 5 6 n-ADD

SIMD (Single Instruction Multiple Data): Working on Data Arrays Array of length n 2 1 9 5 0 7 3 6 … 1 2 8 2 0 9 3 8 0 1 … 4 4 16 2 0 45 0 56 0 6 … 4 8 n-MULT

SIMD (Single Instruction Multiple Data): Working on Data Arrays Array of length n 1 9 5 0 7 3 6 … 1 2 3 6 3 3 4 1 7 8 … 8 5 8 2 0 9 3 8 0 1 … 4 4 % % % % … 2 Great for computing same function F on n different input strings. We can do SIMD homomorphically. Function F

Permuting Encrypted Arrays and Ring Automorphisms

Beyond SIMD Computation Goal: To reduce overhead for a single computation (rather than multiple computations in parallel): Pack all input bits in just a few ciphertexts Compute while keeping everything packed How to do this?

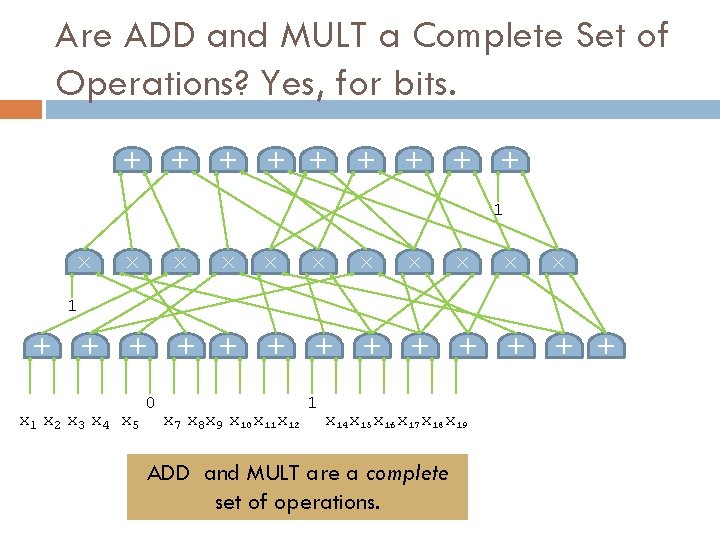
+ + + + + Are ADD and MULT a Complete Set of Operations? Yes, for bits. × × × + + + + × × × + × 1 x 2 x 3 x 4 x 5 0 + + + 1 x 7 x 8 x 9 x 10 x 11 x 12 1 x 14 x 15 x 16 x 17 x 18 x 19 ADD and MULT are a complete set of operations.

+ + + + + Are ADD and MULT a Complete Set of Operations? No, for SIMD arrays. × × × + + + × × × + × 1 x 2 x 3 x 4 x 5 x 1 x 2 x 3 x 4 x 5 0 x 7 x 8 x 9 x 10 x 11 x 12 x 7 + + 1 1 x 8 x 9 x 10 x 11 x 12 x 14 x 15 x 16 x 17 x 18 x 19 x 14 n-ADD and n-MULT are NOT a complete set of operations.

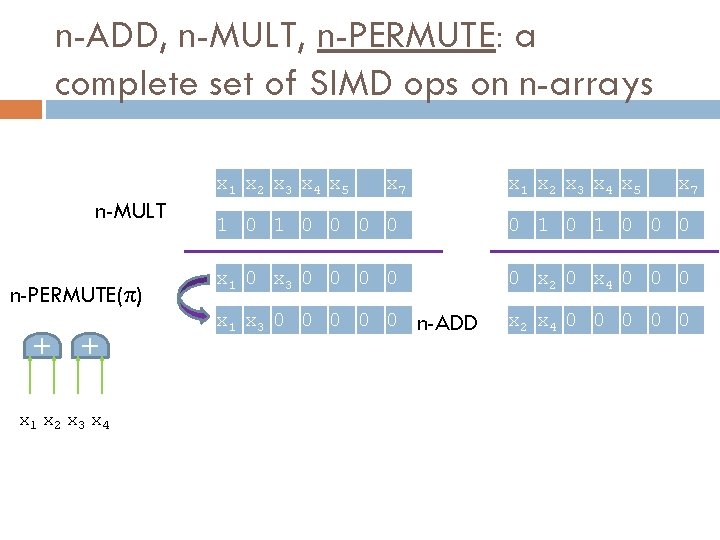
n-ADD, n-MULT, n-PERMUTE: a complete set of SIMD ops on n-arrays n-MULT n-PERMUTE(π) x 1 x 2 x 3 x 4 x 5 x 7 + + x 7 1 0 0 0 x 1 0 x 3 0 0 0 x 2 0 x 4 0 0 0 x 1 x 3 0 0 0 x 1 x 2 x 3 x 4 x 5 n-ADD x 2 x 4 0 0 0

Ring Automorphisms! How do we Evaluate n-Permute(π) homomorphically, without “decompressing” the packed ciphertexts?

Ring Automorphisms If a(x) is “small”, then primeis also “small”. φnk(a(x)) Z[x]/(xn-1), For simplicity, let R = Consider the map φk: R → R given by: φk(a(x)) = a(xk) If gcd(k, p) = 1, φk permutes the coefficients of a(x):

Ring Automorphisms For simplicity, let R = Z[x]/(xn-1), n prime Consider the map φk: R → R given by: φk(a(x)) = a(xk) If gcd(k, p) = 1, φk permutes the coefficients of a(x): φk permutes the evaluations of a(x) at roots of unity: We can use φk to permute our plaintext slots.

Homomorphic Automorphisms

Which Permutations Do the Automorphisms Give Us? The “Basic” Permutations (a(x) → a(xk)): Only n (out of n!) of the possible permutations. Think of the automorphisms as n-ROTATE(i), which rotates the n items i steps clockwise, like a dial. Claim: For any permutation π, we can build n. PERMUTE(π) “efficiently” from n-ADD, n-MULT, and n -ROTATE(i). Benes permutation network

Asymptotic Efficiency Results Overhead of HE = (encrypted comp. time)/(unencrypted comp. time) With ciphertext packing, the overhead of RLWE-based or NTRU-based SWHE for security parameter k: Overhead = poly(log q. L, log w) = poly(L, log k, log w), where L and w are circuit depth and width.

Key Homomorphism and Multikey FHE The Multikey FHE scheme of Lopez-Alt, Tromer, Vaikuntanathan

Recall NTRU Homomorphic Operations

Key Homomorphism in NTRU

LATV Multikey FHE Scheme [LATV 12]: Cloud can (noninteractively) combine data encrypted under different keys. Individual secret keys are s 1, …, sn. Combined secret key is s 1···sn. To decrypt, all users whose data was used must cooperate. Getting FHE: I showed how to combine keys to get multikey SWHE. LATV show to get multikey FHE.

Thank You! Questions? E M I T I RE D P X E ?

Parameters and Running Times

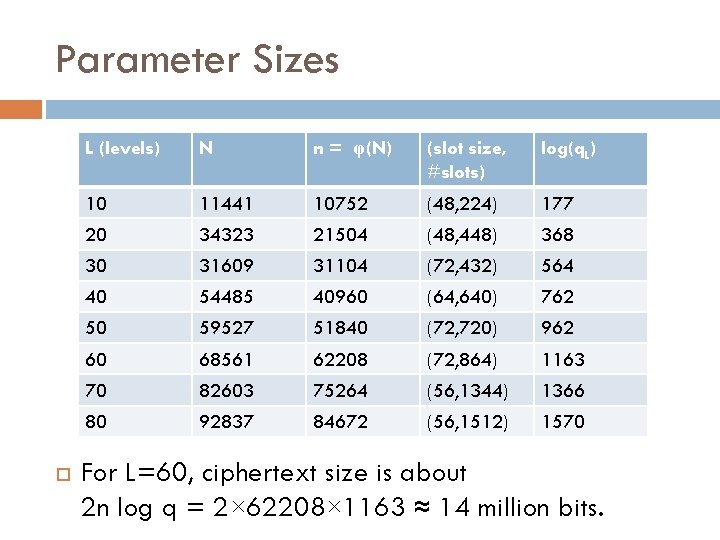
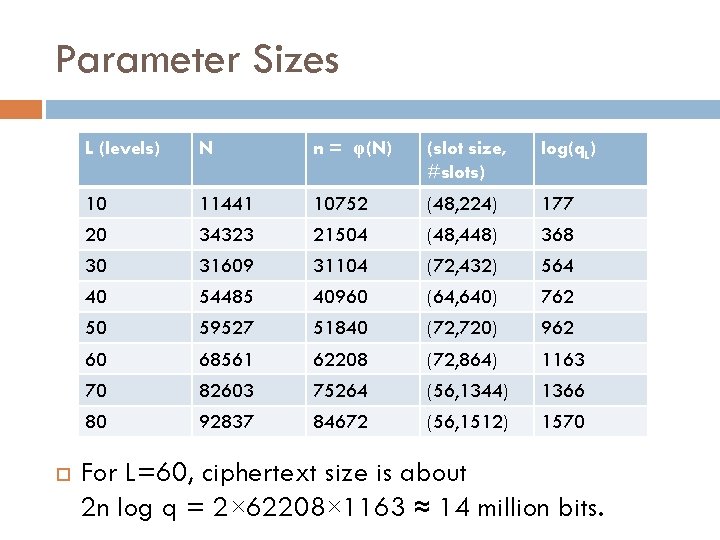
Parameter Sizes L (levels) N n = φ(N) (slot size, #slots) log(q. L) 10 11441 10752 (48, 224) 177 20 34323 21504 (48, 448) 368 30 31609 31104 (72, 432) 564 40 54485 40960 (64, 640) 762 50 59527 51840 (72, 720) 962 60 68561 62208 (72, 864) 1163 70 82603 75264 (56, 1344) 1366 80 92837 84672 (56, 1512) 1570 For L=60, ciphertext size is about 2 n log q = 2× 62208× 1163 ≈ 14 million bits.

Running Times Run a one-core machine with lots of RAM (256 GB) Number of Levels Needed 60 Key Generation 43 minutes Encrypt AES State 2 minutes Encrypt AES Key Schedule 23 minutes Evaluate AES Round 1 7 hours Evaluate AES Round 9 2 hours Evaluate AES Round 10 28 minutes Evaluate AES total 34 hours Number of SIMD Blocks 54 Time Per Block 37 minutes

Parameter Sizes L (levels) N n = φ(N) (slot size, #slots) log(q. L) 10 11441 10752 (48, 224) 177 20 34323 21504 (48, 448) 368 30 31609 31104 (72, 432) 564 40 54485 40960 (64, 640) 762 50 59527 51840 (72, 720) 962 60 68561 62208 (72, 864) 1163 70 82603 75264 (56, 1344) 1366 80 92837 84672 (56, 1512) 1570 For L=60, ciphertext size is about 2 n log q = 2× 62208× 1163 ≈ 14 million bits.

Running Times Run a one-core machine with lots of RAM (256 GB) Number of Levels Needed 60 Key Generation 43 minutes Encrypt AES State 2 minutes Encrypt AES Key Schedule 23 minutes Evaluate AES Round 1 7 hours Evaluate AES Round 9 2 hours Evaluate AES Round 10 28 minutes Evaluate AES total 34 hours Number of SIMD Blocks 54 Time Per Block 37 minutes