Fully Homomorphic Encryption over the Integers Many slides

Fully Homomorphic Encryption over the Integers Many slides borrowed from Craig Marten van Dijk 1, Craig Gentry 2, Shai Halevi 2, Vinod Vaikuntanathan 2 1 – MIT, 2 – IBM Research

Computing on Encrypted Data q Storing my files on the cloud n n Encrypt them to protect my information Search through them for emails with “homomorphic” in the subject line Ø q Cloud should return only these (encrypted) messages, w/o knowing the key Private Internet search n n Encrypt my query, send to Google I still want to get the same results Ø Results would be encrypted too

Public-key Encryption q Three procedures: Key. Gen, Enc, Dec n (sk, pk) Key. Gen($) Ø n c Encpk(m) Ø n Encrypt a message with the public key m Decsk(c) Ø q Generate random public/secret key-pair Decrypt a ciphertext with the secret key E. g. , RSA: c me mod N, m cd mod N n (N, e) public key, d secret key

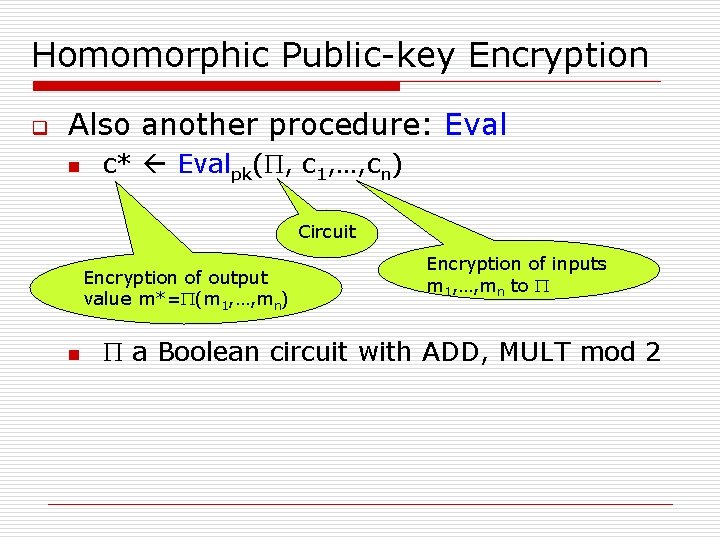
Homomorphic Public-key Encryption q Also another procedure: Eval n c* Evalpk(P, c 1, …, cn) Circuit Encryption of output value m*=P(m 1, …, mn) n Encryption of inputs m 1, …, mn to P P a Boolean circuit with ADD, MULT mod 2

An Analogy: Alice’s Jewelry Store q q Alice’s workers need to assemble raw materials into jewelry But Alice is worried about theft How can the workers process the raw materials without having access to them?

An Analogy: Alice’s Jewelry Store q Alice puts materials in locked glove box n q q For which only she has the key Workers assemble jewelry in the box Alice unlocks box to get “results”

The Analogy q Enc: putting things inside the box n n q Dec: Taking things out of the box n n q Only Alice can do it, requires the key m* Decsk(c*) Eval: Assembling the jewelry n n q Anyone can do this (imagine a mail-drop) ci Encpk(mi) Anyone can do it, computing on ciphertext c* Evalpk(P, c 1, …, cn) m* = P(m 1, …, mn) is “the ring”, made from “raw materials” m 1, …, mn

Can we do it? q As described so far, sure. . n n (P, c 1, …, cn) = c* Evalpk(P, c 1, …, cn) Decsk(c*) decrypts individual ci’s, apply P (the workers do nothing, Alice assembles the jewelry by herself) This is the main challenge Of course, this is cheating: q We want c* to remain small n n q independent of the size of P “Compact” homomorphic encryption We may also want P to remain secret Can be done with “generic tools” (Yao’s garbled circuits)

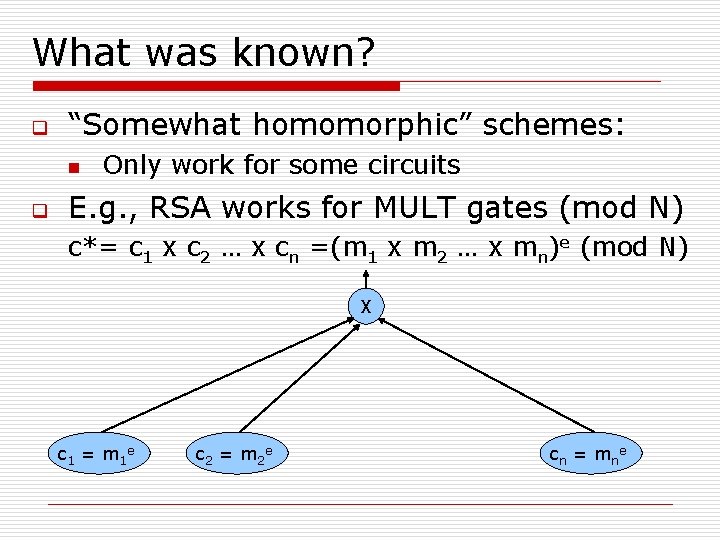
What was known? q “Somewhat homomorphic” schemes: n q Only work for some circuits E. g. , RSA works for MULT gates (mod N) c*= c 1 x c 2 … x cn =(m 1 x m 2 … x mn)e (mod N) X c 1 = m 1 e c 2 = m 2 e cn = mne

“Somewhat Homomorphic” Schemes q q RSA, El. Gamal work for MULT mod N Go. Mi, Paillier work for XOR, ADD BGN 05 works for quadratic formulas SYY 99 works for shallow fan-in-2 circuits n q q c* grows exponentially with the depth of P IP 07 works for branching program MGH 08 works for low-degree polynomials n c* grows exponentially with degree

A Recent Breakthrough q Genrty 09: A bootstrapping technique Somewhat homomorphic → Fully homomorphic Scheme E can evaluate its own decryption circuit q Scheme E* can evaluate any circuit Gentry also described a candidate “bootstrappable” scheme n Based on ideal lattices

The Current Work q A second “bootstrappable” scheme n q Very simple: using only modular arithmetic Security is based on the hardness of finding “approximate-GCD”

Outline 1. A homomorphic symmetric encryption 2. Turning it into public-key encryption n 3. Result is “almost bootstrappable” Making it bootstrappable n Similar to Gentry’ 09 Time permitting 4. Security 5. Gentry’s bootstrapping technique Not today

A homomorphic symmetric encryption q Shared secret key: odd number p q To encrypt a bit m: n n Choose at random large q, small r 2 r+m much Output c = pq + 2 r + m smaller than p Ø Ø q Ciphertext is close to a multiple of p m = LSB of distance to nearest multiple of p To decrypt c: n Output m = (c mod p) mod 2

Why is this homomorphic? q c 1=q 1 p+2 r 1+m 1, c 2=q 2 p+2 r 2+m 2 Distance to nearest multiple of p q c 1+c 2 = (q 1+q 2)p + 2(r 1+r 2) + (m 1+m 2) 2(r 1+r 2)+(m 1+m 2) still much smaller than p c 1+c 2 mod p = 2(r 1+r 2) + (m 1+m 2) n q c 1 x c 2 = (c 1 q 2+q 1 c 2 -q 1 q 2)p + 2(2 r 1 r 2+r 1 m 2+m 1 r 2) + m 1 m 2 2(2 r 1 r 2+…) still much smaller than p c 1 xc 2 mod p = 2(2 r 1 r 2+…) + m 1 m 2 n

How homomorphic is this? q Can keep adding and multiplying until the “noise term” grows larger than q/2 n q Noise doubles on addition, squares on multiplication We choose r ~ n 2 n, p~ 2 n 2 (and q ~ 5 n 2 ) Can compute polynomials of degree ~n before the noise grows too large

Homomorphic Public-Key Encryption q Secret key is an odd p as before q Public key is many “encryptions of 0” n q q q xi = [qip + 2 ri ]x 0 for i=1, 2, …, n Encpk(m) = [subset-sum(xi’s)+m+2 r]x 0 Decsk(c) = (c mod p) mod 2 Eval as before

Bootstrappable yet? c/p, rounded to nearest integer q Almost, but not quite: q Decryption is m = c – (p x [c/p]) mod 2 n n n Same as c–[c/p] mod 2, since p is odd Computing [c/p] mod 2 takes degree O(n) But O() has constant bigger than one Ø q Our scheme only supports degree < n To get a bootstrappable scheme, use Gentry 09 technique to “squash the decryption circuit”

Security q The approximate-GCD problem: n Input: integers x 1, x 2, x 3, … Ø Ø n q Chosen as xi = qip + ri for a secret odd p p $[0, P], qi $[0, Q], ri $[0, R] (with R P Q) Task: find p Thm: If we can distinguish Enc(0)/Enc(1) for some p, then we can find that p Roughly: the LSB of ri is a “hard core bit” Scheme is secure if approx-GCD is hard n q Is approx-GCD really a hard problem?

Hardness of Approximate-GCD q Several lattice-based approaches for solving approximate-GCD n n Related to Simultaneous Diophantine Approximation (SDA) Studied in [Hawgrave-Graham 01] Ø q We considered some extensions of his attacks All run out of steam when |qi|>|p|2 n In our case |p|~n 2, |qi|~n 5 |p|2

Relation to SDA q xi = qip + ri (ri p qi), i = 0, 1, 2, … n n yi = xi/x 0 = (qi+si)/q 0, si ~ ri/p 1 y 1, y 2, … is an instance of SDA Ø q q 0 is a denominator that approximates all yi’s Use Lagarias’es algorithm: n n Consider the rows of this matrix: Find a short vector in the R x 1 x 2 … xt -x 0 lattice that they span L= -x 0 <q 0, q 1, …, qt>·L is short … Hopefully we will find it -x 0

Relation to SDA (cont. ) q When will Lagarias’es algorithm succeed? n <q 0, q 1, …, qt>·L should be shortest in lattice Ø n n In particular shorter than ~det(L)1/t+1 This only holds for t > log Q/log P Minkowsk i bound The dimension of the lattice is t+1 Quality of lattice-reduction deteriorates exponentially with t When log Q > (log P)2 (so t>log P), LLL-type reduction isn’t good enough anymore

Conclusions q q Fully Homomorphic Encryption is a very powerful tool Gentry 09 gives first feasibility result n q q Showing that it can be done “in principle” We describe a “conceptually simpler” scheme, using only modular arithmetic What about efficiency? n Computation, ciphertext-expansion are polynomial, but a rather large one…

Thank you