Homomorphic Encryption Mike Merry Motivations for homomorphic encryption

Homomorphic Encryption Mike Merry

• Motivations for homomorphic encryption • What do we need? • What is homomorphic encryption? • How do we make it work? • An example of how to do it

• Motivations for homomorphic encryption • What is necessary? • What is homomorphic encryption? • How do we make it work? • An example of how to do it

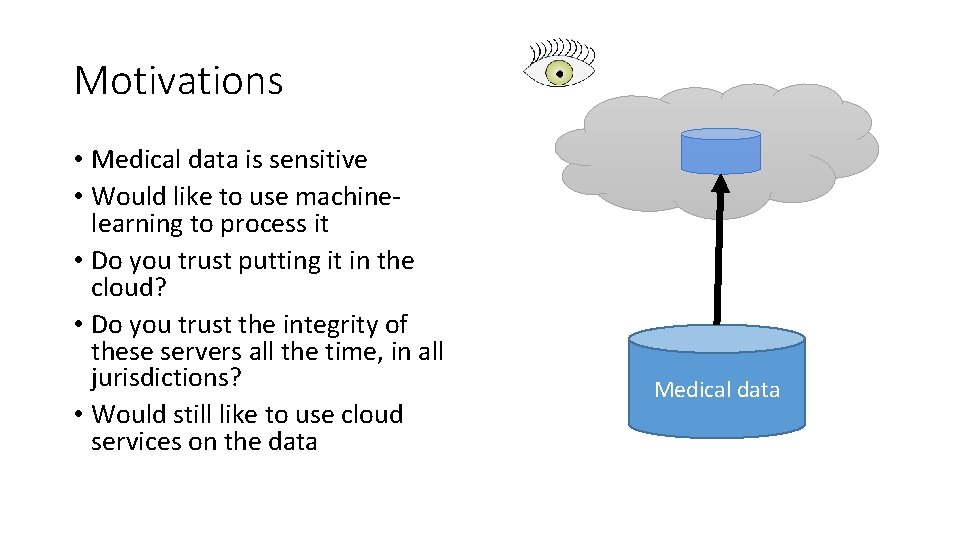
Motivations • Medical data is sensitive • Would like to use machinelearning to process it • Do you trust putting it in the cloud? • Do you trust the integrity of these servers all the time, in all jurisdictions? • Would still like to use cloud services on the data Medical data

e’ e Enc(k, m = e) Dec(k, e) = m m f(m) m’

g(e) e’ e Enc(k, m = e) Dec(k, e) = m m f(m) m’

g(e) e’ e Enc(k, m = e) Dec(k, e) = m m f(m) m’

• Motivations for homomorphic encryption • What do we need? • What is homomorphic encryption? • How do we make it work? • An example of how to do it

What do we need? • Process data: • • In any way we want On an insecure environment Without leaking information about the data In a time- and space-efficient manner • We are not (necessarily) concerned with hiding what we are doing • This is called Functional Encryption (FE) and is related, but distinct

• Motivations for homomorphic encryption • What do we need? • What is homomorphic encryption? • How do we make it work? • An example of how to do it

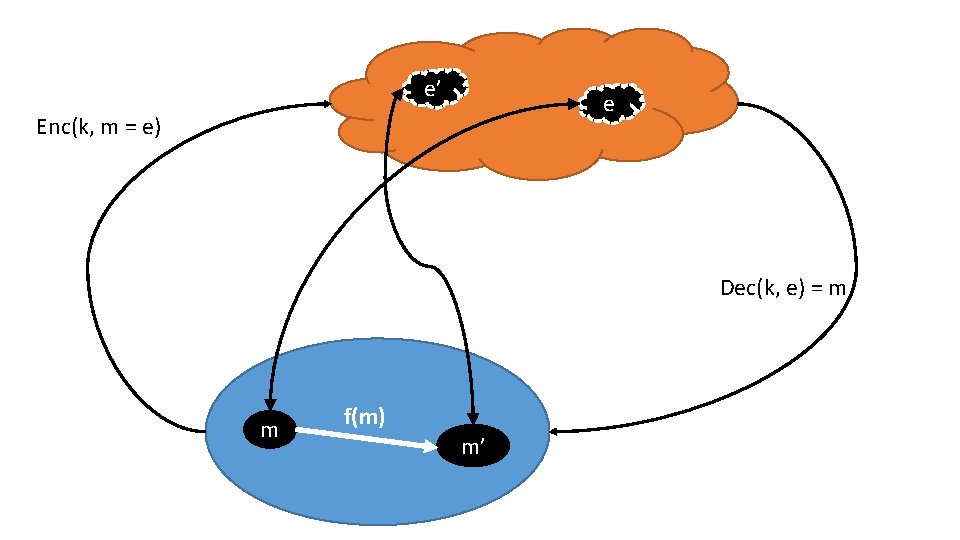
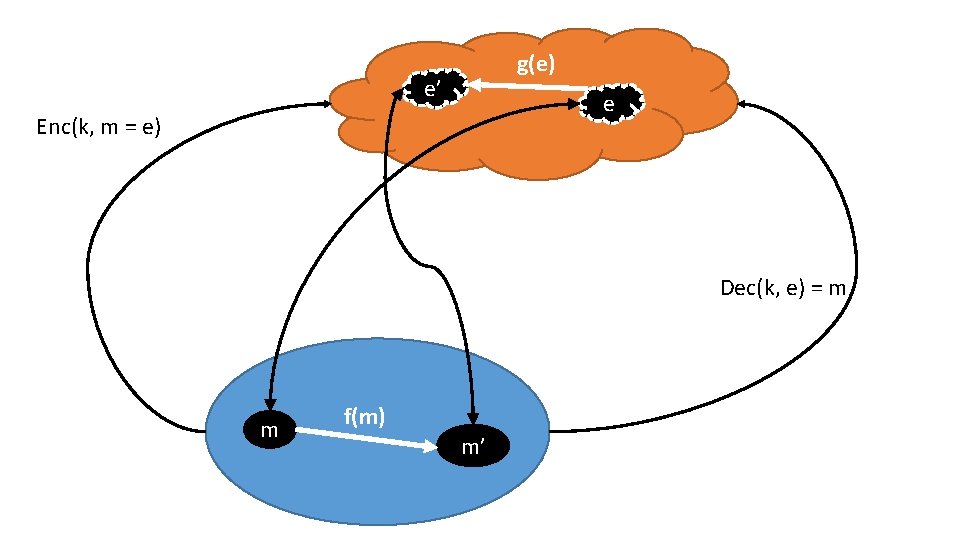
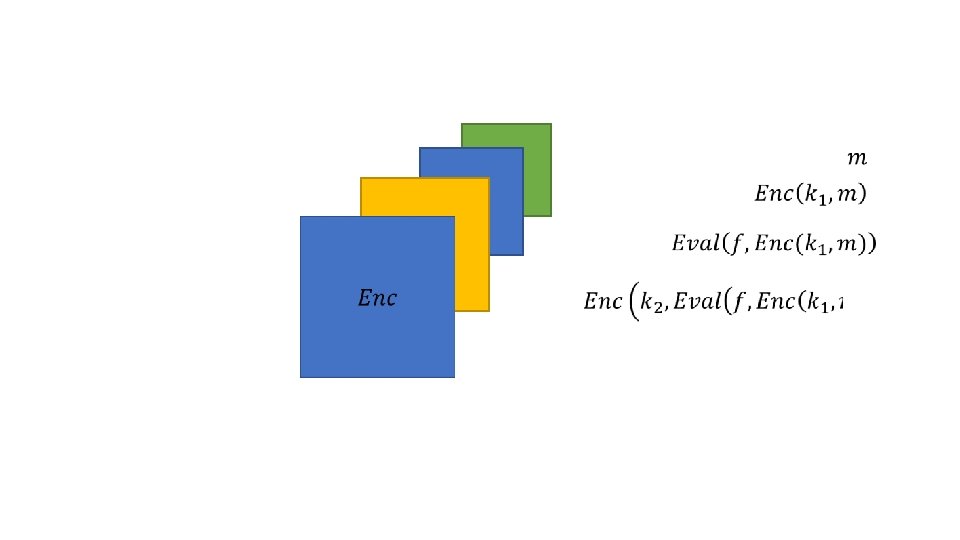
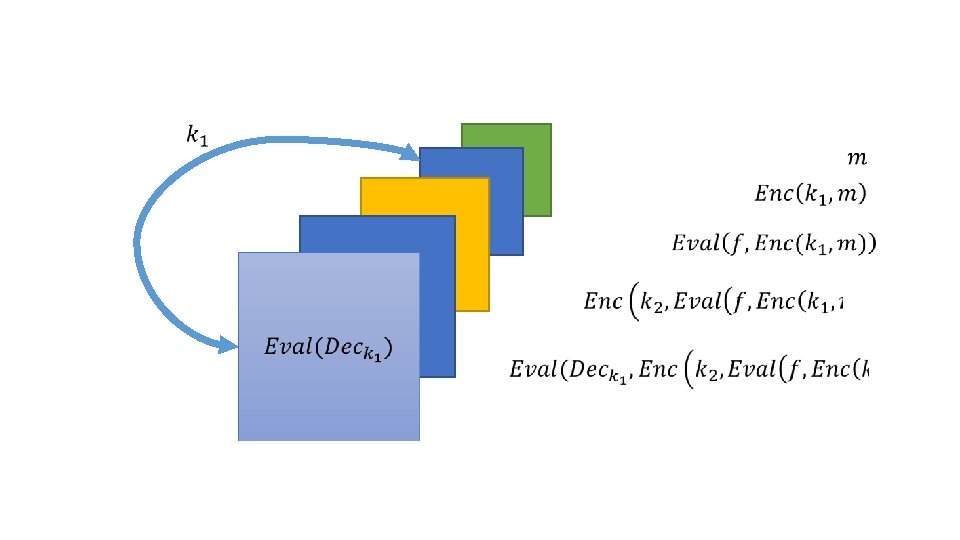
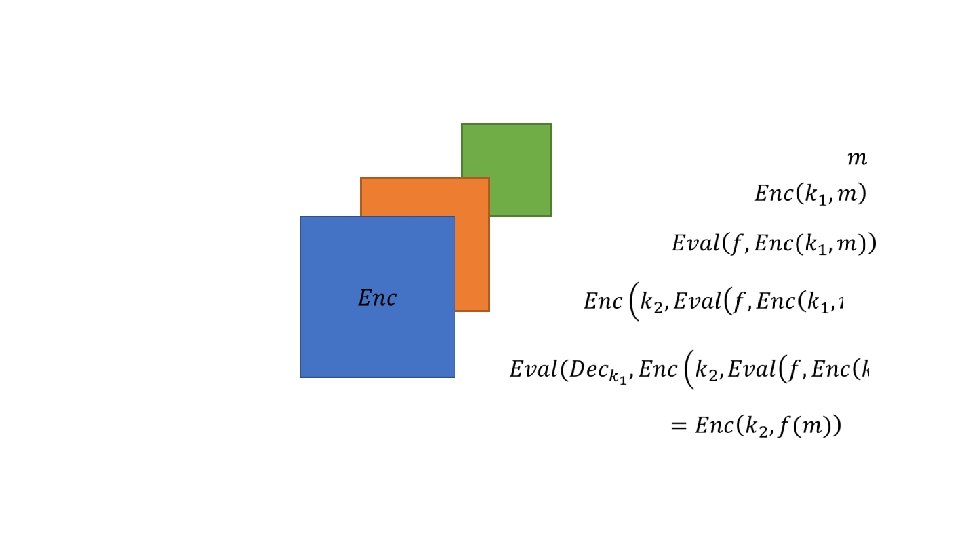
A (reasonably loose) definition • Let U be unencrypted space, and be E encrypted space. Let f: U → U be a function that we want to compute on our data • We would like to find g: E → E such that g(e) = Enc(k, f(m)), that is efficient and secure

A formal definition [1] • [1] Armknecht, F. , Boyd, C. , Carr, C. , Gjosteen, K. , Jaschke, A. , Reuter, C. A. , & Strand, M. (2015). A Guide to Fully Homomorphic Encryption. Cryptology e. Print Archive, 1– 35. Retrieved from https: //eprint. iacr. org/2015/1192

Properties: correctness •

Properties: Compactness •

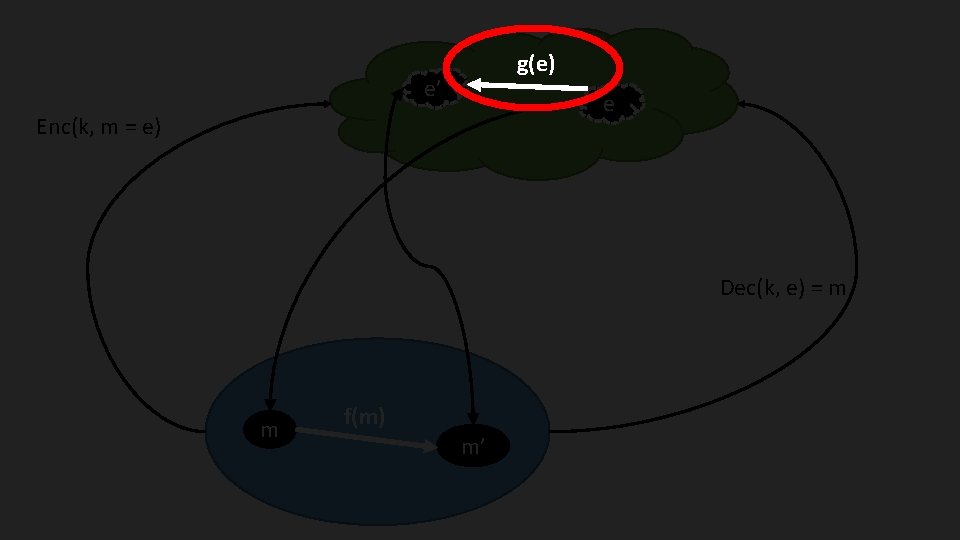
Properties: Privacy • Circuit privacy: The distribution of the evaluation of a circuit in homomorphic space is indistinguishable from the encryption of the output of the circuit • A different way of viewing Circuit Privacy is to consider whether you would be happy to release the encrypted results of a message-space function. If you would, then as the distribution of the evaluation space is the same, you should be happy to release those results as well. • This doesn’t mean the distributions are equivalent to fresh cipher texts as the distribution of f(x) is not random.

• Motivations for homomorphic encryption • What do we need? • What is homomorphic encryption? • How do we make it work? • An example of how to do it

Bootstrapping [2] • [2] Gentry, C. (2009). Fully homomorphic encryption using ideal lattices. In Proceedings of the 41 st annual ACM symposium on Symposium on theory of computing - STOC ’ 09 (Vol. 19, p. 169). New York, USA: ACM Press.

m

• Motivations for homomorphic encryption • What do we need? • What is homomorphic encryption? • How do we make it work? • An example of how to do it

Dijk and Gentry’s FHE over the integers [3] • [3] Van Dijk, M. , Gentry, C. , Halevi, S. , & Vaikuntanathan, V. (2010). Fully Homomorphic Encryption over the Integers. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 24– 43). Springer Berlin Heidelberg. http: //doi. org/10. 1007/978 -3 -642 -13190 -5_2

Dijk and Gentry’s FHE over the integers •

Dijk and Gentry’s FHE over the integers •

References 1. Armknecht, F. , Boyd, C. , Carr, C. , Gjosteen, K. , Jaschke, A. , Reuter, C. A. , & Strand, M. (2015). A Guide to Fully Homomorphic Encryption. Cryptology e. Print Archive, 1– 35. Retrieved from https: //eprint. iacr. org/2015/1192 2. Gentry, C. (2009). Fully homomorphic encryption using ideal lattices. In Proceedings of the 41 st annual ACM symposium on Symposium on theory of computing - STOC ’ 09 (Vol. 19, p. 169). New York, USA: ACM Press. http: //doi. org/10. 1145/1536414. 1536440 3. Van Dijk, M. , Gentry, C. , Halevi, S. , & Vaikuntanathan, V. (2010). Fully Homomorphic Encryption over the Integers. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 24– 43). Springer Berlin Heidelberg. http: //doi. org/10. 1007/978 -3642 -13190 -5_2