FULLY HOMOMORPHIC ENCRYPTION from the Integers Marten van

FULLY HOMOMORPHIC ENCRYPTION from the Integers Marten van Dijk (RSA labs) Craig Gentry (IBM T J Watson) Shai Halevi Vinod Vaikuntanathan (IBM T J Watson)

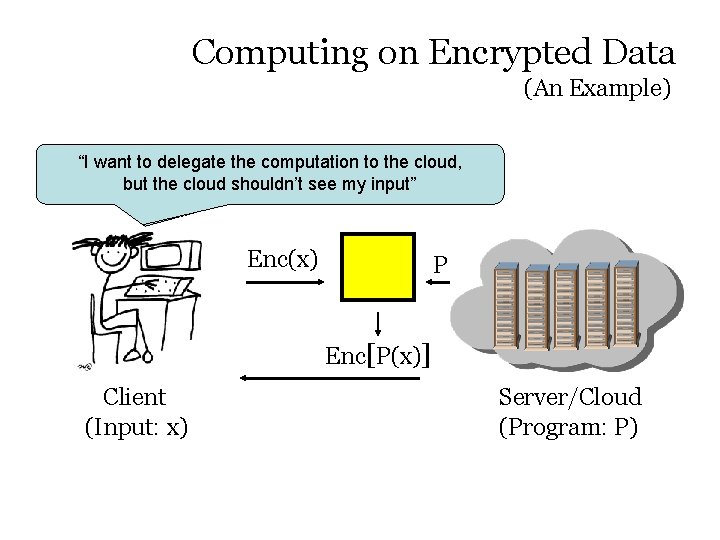
Computing on Encrypted Data (An Example) “I want to delegate the computation to the cloud, the cloudthe shouldn’t see my “I wantbut to delegate computation toinput” the cloud” Enc(x) P Enc[P(x)] Client (Input: x) Server/Cloud (Program: P)

= Fully. Homomorphic Encryption (FHE) Eval P Enc(x) Definition: [Key. Gen, Enc, Dec, ]Eval] (as in regular encryption) Enc[P(x)] Compactness: Size of Eval’ed ciphertext independent of P Security: Semantic Security [GM’ 82]

Fully Homomorphic Encryption ► First Defined: “Privacy homomorphism” [RAD’ 78] – their motivation : searching encrypted data ► Limited Variants: – RSA & El Gamal: multiplicatively homomorphic – GM & Paillier: additively homomorphic – BGN’ 05 & GHV’ 10 a: quadratic formulas ► NON-COMPACThomomorphic encryption [CCKM 00, SYY 99, IP 07, MGH 08, GHV 10 b, …]

Fully Homomorphic Encryption ► First Defined: “Privacy homomorphism” [RAD’ 78] – their motivation : searching encrypted data Big Breakthrough : [Gentry 09] First Construction of Fully Homomorphic Encryption using algebraic number theory / “ideal lattices” No ideal lattices ► Is there an elementary. Construction of FHE? – using just integer addition and multiplication – easier to understand, implement and improve

OUR RESULT Theorem[DGHV’ 10]: We have a fully homomorphic public-key encryption scheme – which uses only add and mult over the integers, – which is secure based on the approximate GCD problem & the sparse subset sum problem.

Construction

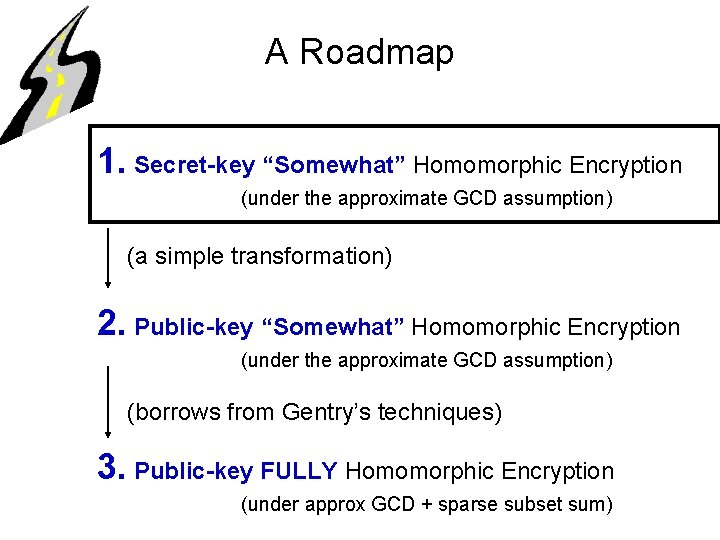
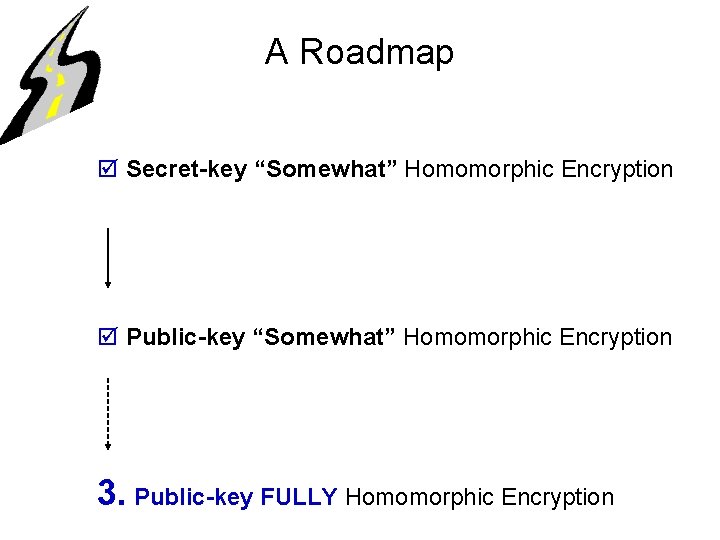
A Roadmap 1. Secret-key “Somewhat” Homomorphic Encryption (under the approximate GCD assumption) (a simple transformation) 2. Public-key “Somewhat” Homomorphic Encryption (under the approximate GCD assumption) (borrows from Gentry’s techniques) 3. Public-key FULLY Homomorphic Encryption (under approx GCD + sparse subset sum)

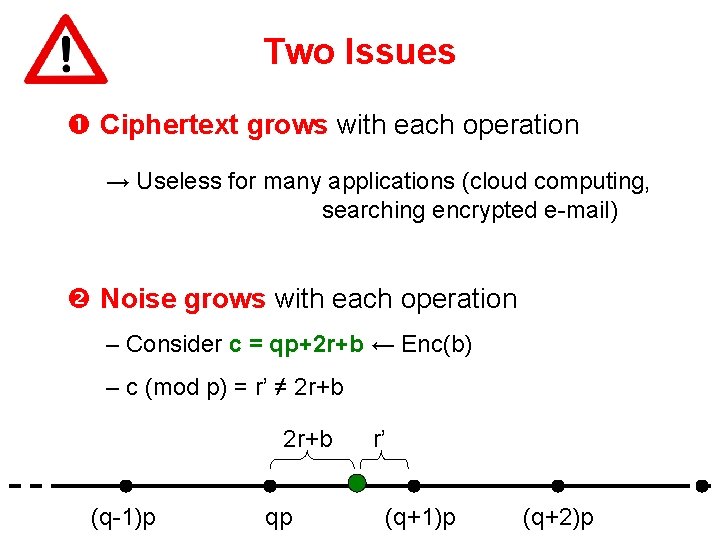
Secret-key Homomorphic Encryption Secret key: an n 2 -bit odd number p (sec. param = n) To Encrypt a bit b: – pick a random “large” multiple of p, say q·p (q ~ n 5 bits) (r ~ n bits) – pick a random “small” even number 2·r – Ciphertext c = q·p+2·r+b “noise” To Decrypt a ciphertext c: – c (mod p) = 2·r+b – read off the least significant bit

Secret-key Homomorphic Encryption How to Add and Multiply Encrypted Bits: – Add/Mult two near-multiples of p gives a near-multiple of p – c 1 = q 1·p + (2·r 1 + b 1), c 2 = q 2·p + (2·r 2 + b 2) – c 1+c 2 = p·(q 1 + q 2) + 2·(r 1+r 2) + (b 1+b 2) «p LSB = b 1 XOR b 2 – c 1 c 2 = p·(c 2·q 1+c 1·q 2 -q 1·q 2) + 2·(r 1 r 2+r 1 b 2+r 2 b 1) + b 1 b 2 « p LSB = b 1 AND b 2

Two Issues Ciphertext grows with each operation → Useless for many applications (cloud computing, searching encrypted e-mail) Noise grows with each operation – Consider c = qp+2 r+b ← Enc(b) – c (mod p) = r’ ≠ 2 r+b (q-1)p qp r’ (q+1)p (q+2)p

Two Issues Ciphertext grows with each operation → Useless for many applications (cloud computing, searching encrypted e-mail) Noise grows with each operation → After some operations, the ciphertext becomes “undecryptable”

Solving the Two Issues Ciphertext grows with each operation – Publish x 0 = q 0 p (*) – Take ciphertext (mod x 0) after each op (Add/Mult) (*) More complex way using x 0 = a near-multiple of p

Solving the Two Issues Ciphertext grows with each operation – Publish x 0 = q 0 p – Take ciphertext (mod x 0) after each op (Add/Mult) v Ciphertext stays less than x 0 always v The encrypted bit remains same v Noise does not increase at all

Solving the Two Issues Ciphertext grows with each operation – Publish x 0 = q 0 p – Take ciphertext (mod x 0) after each op (Add/Mult)* Noise grows with each operation v Can perform “limited” number of hom. operations (“Somewhat Homomorphic” Encryption) – Somewhat → Fully: (A variant of) Squashing + Bootstrapping [G’ 09]

Security (of the secret-key “somewhat” homomorphic scheme)

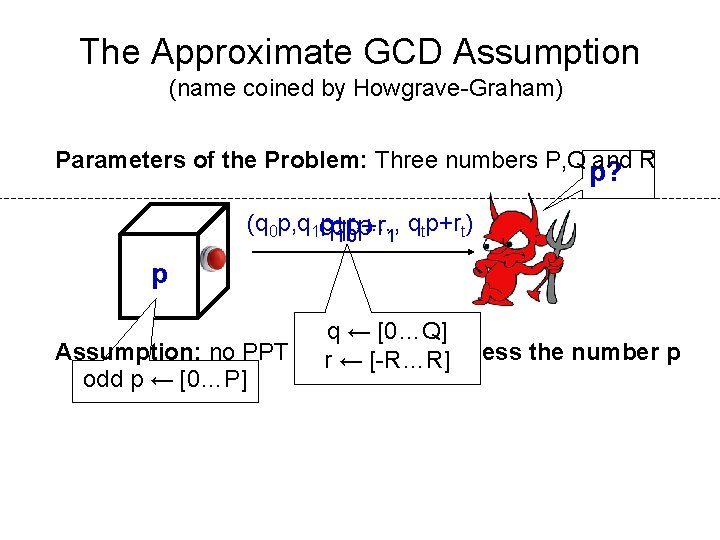
The Approximate GCD Assumption (name coined by Howgrave-Graham) Parameters of the Problem: Three numbers P, Q and R p? (q 0 p, q 1 q p+r , …, q p+rt) q 1 p+r 01 p 1 t p qq 0 ← ← [0…Q] Assumption: no PPT adversary can guess the number p r ← [-R…R] odd p ← [0…P]

(q 0 p, q 1 p+r 1, …, qtp+rt) p? p Assumption: no PPT adversary can guess the number p = (proof of security) Semantic Security: no PPT adversary can guess the bit b (q 0 p, q 1 p+2 r 1+b, …, qkp+2 rk+b)

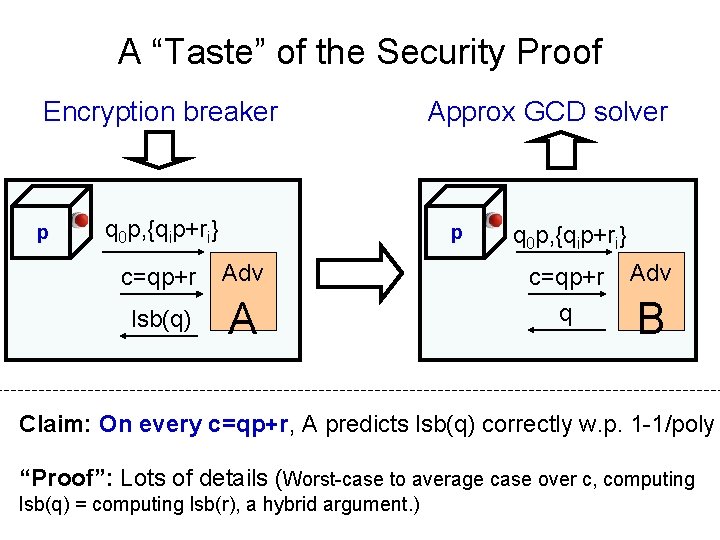
A “Taste” of the Security Proof Encryption breaker p q 0 p, {qip+ri} Approx GCD solver p q 0 p, {qip+ri} c=qp+r Adv lsb(q) A q B Claim: On every c=qp+r, A predicts lsb(q) correctly w. p. 1 -1/poly “Proof”: Lots of details (Worst-case to average case over c, computing lsb(q) = computing lsb(r), a hybrid argument. )

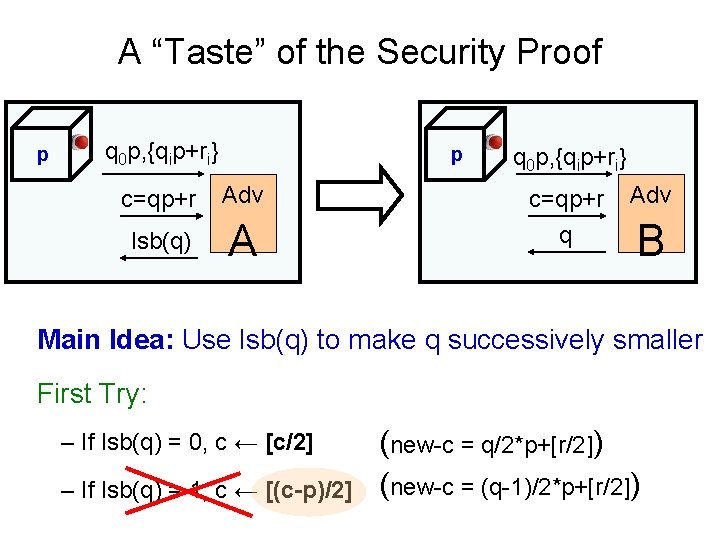
A “Taste” of the Security Proof p q 0 p, {qip+ri} p c=qp+r Adv lsb(q) A q 0 p, {qip+ri} c=qp+r q Adv B Main Idea: Use lsb(q) to make q successively smaller First Try: – If lsb(q) = 0, c ← [c/2] – If lsb(q) = 1, c ← [(c-p)/2] (new-c = q/2*p+[r/2]) (new-c = (q-1)/2*p+[r/2])

A “Taste” of the Security Proof Main Idea: Use lsb(q) to make q successively smaller Lemma: Given two near-multiples z 1=q 1 p+r 1 and z 2=q 2 p+r 2 (+lsb oracle), can compute z’=gcd(q 1, q 2)·p+r’ for small r’ W. h. p. gcd(q 1, q 2)=1 – If lsb(q) = 0, c ← [c/2] – If lsb(q) = 1, c ← [(c-z’)/2] [(c-p)/2] – Learn q bit by bit (new-c = q/2*p+[r/2]) (new-c = (q-1)/2*p+[(r-r’)/2] (q-1)/2*p+[r/2]) )

A “Taste” of the Security Proof Main Idea: Use lsb(q) to make q successively smaller Lemma: Given two near-multiples z 1=q 1 p+r 1 and z 2=q 2 p+r 2 (+lsb oracle), can compute z’=gcd(q 1, q 2)·p+r’ for small r’ Observation: the Binary GCD algo. is “noise-tolerant”, given lsb oracle. (similar to the RSA hardcore bit proof of [ACGS’ 88])

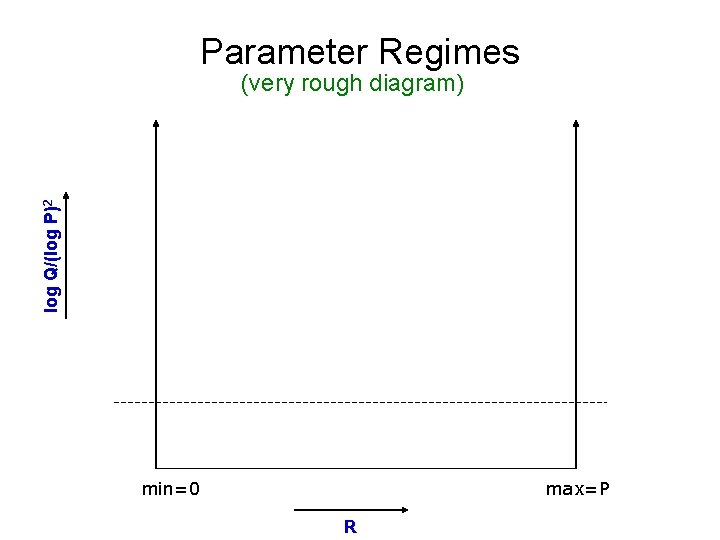
How Hard is Approximate GCD? v Studied by [HG 01]; also [Lag 82, Cop 97, NS 01] (equivalent to “simultaneous Diophantine approximation”) v Lattice-based Attacks – Lagarias’ algorithm – Coppersmith’s algo. for finding small polynomial roots – Nguyen/Stern and Regev’s orthogonal lattice method v All run out of steam when log Q > (log P)2 (our setting of parameters: log Q = n 5, log P = n 2)

Future Directions Efficient fully homomorphic encryption (Currently: n 5 size ciphertexts; n 10 running-time blowup) Some recent improvements [SV’ 10, SS’ 10] Security of the approx GCD assumption (e. g. , a worst-case to average-case reduction to regular – non-ideal – lattice problems? )

Questions?

Public-key Homomorphic Encryption Secret key: an n 2 -bit odd number p Δ Public key: [q 0 p+2 r 0, q 1 p+2 r 1, …, qtp+2 rt] = (x 0, x 1, …, xt) = t+1 random encryptions of 0 To Decrypt a ciphertext c: – c (mod p) = 2·r+b – read off the least significant bit Eval (as before)

Public-key Homomorphic Encryption Secret key: an n 2 -bit odd number p Δ Public key: [q 0 p+2 r 0, q 1 p+2 r 1, …, qtp+2 rt] = (x 0, x 1, …, xt) To Encrypt a bit b: pick random subset S c= + b (mod x 0) To Decrypt a ciphertext c: – c (mod p) = 2·r+b – read off the least significant bit Eval (as before) [1…t]

Parameter Regimes log Q/(log P)2 (very rough diagram) min=0 max=P R

Public-key Homomorphic Encryption Secret key: an n 2 -bit odd number p Δ Public key: [q 0 p+2 r 0, q 1 p+2 r 1, …, qtp+2 rt] = (x 0, x 1, …, xt) – t+1 encryptions of 0 – W. l. o. g. , x 0 = q 0 p+2 r 0 is the largest To Decrypt a ciphertext c: – c (mod p) = 2·r+b – read off the least significant bit Eval (as before)

Public-key Homomorphic Encryption Secret key: an n 2 -bit odd number p Δ Public key: [q 0 p+2 r 0, q 1 p+2 r 1, …, qtp+2 rt] = (x 0, x 1, …, xt) To Encrypt a bit b: pick random subset S c= [1…t] + b (mod x 0) To Decrypt a ciphertext c: (mod x 0) a small k) = p[p) = 2·r+b ] + 2[ +b– kx 0 (for – c c(mod p) =] 2·r+b – read= off p[ the least significant ] + 2[ bit ]+b of p) + (“small” even noise) + b Eval (as (mult. before)

Public-key Ciphertext Homomorphic Size Reduction Encryption Secret key: an n 2 -bit odd number p Δ Public key: [q 0 p+2 r 0, q 1 p+2 r 1, …, qtp+2 rt] = (x 0, x 1, …, xt) To Encrypt a bit b: pick random subset S [1…t] – Resulting ciphertext < x 0 c= + b (mod x 0) – Underlying bit is the same (since x 0 has even noise) –To. Noise Decrypt ciphertext c: by much(*) doesa not increase – c (mod p) = 2·r+b – read off the least significant bit Eval: Reduce mod x 0 after each operation (*) additional tricks for mult

A Roadmap þ Secret-key “Somewhat” Homomorphic Encryption þ Public-key “Somewhat” Homomorphic Encryption 3. Public-key FULLY Homomorphic Encryption

How “Somewhat” Homomorphic is this? Can evaluate (multi-variate) polynomials with m terms, and maximum degree d if: or f(x 1, …, xt) = x 1·x 2·xd + … + xt-d+1·xt-d+2·xt Say, noise in Enc(xi) < 2 n Final Noise ~ (2 n)d+…+(2 n)d = m • (2 n)d

From “Somewhat” to “Fully” Theorem [Gentry’ 09]: Convert “bootstrappable” → FHE = Can eval all fns. Augmented Decryption ckt. “Somewhat” HE “Bootstrappable” NAND Dec c 1 sk Dec c 2 sk

Is our Scheme “Bootstrappable”? What functions can the scheme EVAL? (polynomials of degree < n) (? ) Complexity of the (aug. ) Decryption Circuit (degree ~ n 1. 73 polynomial) Can be made bootstrappable – Similar to Gentry’ 09 Caveat: Assume Hardness of “Sparse Subset Sum”