Integers and Algorithms The Integers and Division Integers

강의 내용 Integers and Algorithms 정수와 나눗셈(The Integers and Division) 정수와 알고리즘(Integers and Algorithms) Page 2 Discrete Mathematics by Yang-Sae Moon

Introduction The Integers and Division Of course you already know what the integers are, and what division is… (정수와 나누기… 다 아는거~) But: There are some specific notations, terminology, and theorems associated with these concepts which you may not know. (몇 가지 주요 표기, 용어, 정리 등을 배웁시다. ) These form the basics of number theory. (정수론의 기초. . ) • Vital in many important algorithms today (hash functions, cryptography, digital signatures). Page 3 Discrete Mathematics by Yang-Sae Moon

Divides, Factor, and Multiple The Integers and Division Let a, b Z with a 0. a|b “a divides b” : “ c Z: b=ac” “There is an integer c such that c times a equals b. ” (b가 a로 나누어짐(a로 b를 나눌 수 있음)을 의미하며, 이때 몫이 c이다. ) • Example: 3 12 True, but 3 7 False. 인수 If a divides b, then we say a is a factor or a divisor of b, and b is a multiple of a. 배수 “b is even” : ≡ 2 b. Is 0 even? Is − 4? Page 4 Discrete Mathematics by Yang-Sae Moon

Some Facts of Division The Integers and Division a, b, c Z: 1. a|0 (2|0, 3|0, …) 2. (a|b a|c) a | (b + c) (2|4 2|6 2|10) 3. a|bc (2|4 2|4∙ 3) 4. (a|b b|c) a|c (2|4 4|8 2|8) Proof of (2): • a|b means there is an s such that b=as, • and a|c means that there is a t such that c=at, • so b+c = as+at = a(s+t), so a|(b+c) also. □ Page 5 Discrete Mathematics by Yang-Sae Moon

More Detailed Version of Proof The Integers and Division Show a, b, c Z: (a|b a|c) a | (b + c). Let a, b, c be any integers such that a|b and a|c, and show that a | (b + c). By definition of |, we know s: b=as, and t: c=at. Let s, t, be such integers. Then b+c = as + at = a(s+t) so u: b+c=au, namely u=s+t. Thus a|(b+c). Page 6 Discrete Mathematics by Yang-Sae Moon

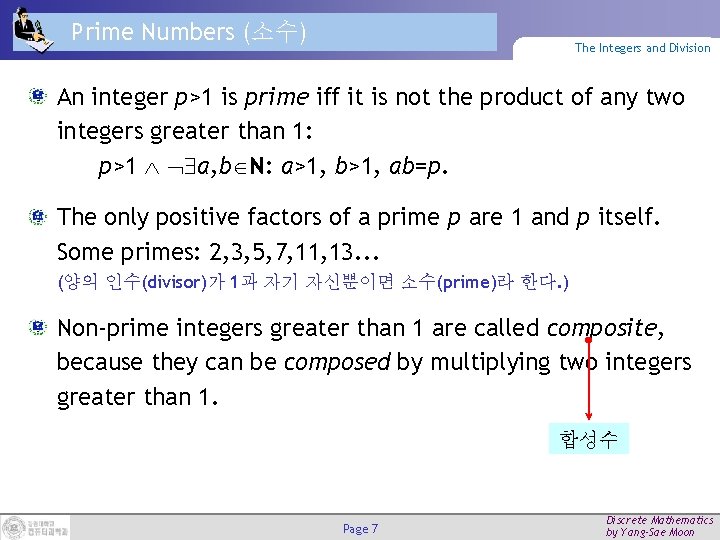
Prime Numbers (소수) The Integers and Division An integer p>1 is prime iff it is not the product of any two integers greater than 1: p>1 a, b N: a>1, b>1, ab=p. The only positive factors of a prime p are 1 and p itself. Some primes: 2, 3, 5, 7, 11, 13. . . (양의 인수(divisor)가 1과 자기 자신뿐이면 소수(prime)라 한다. ) Non-prime integers greater than 1 are called composite, because they can be composed by multiplying two integers greater than 1. 합성수 Page 7 Discrete Mathematics by Yang-Sae Moon

Fundamental Theorem of Arithmetic (산술의 기본 정리) The Integers and Division Every positive integer has a unique representation as the product of a non-decreasing series of zero or more primes. (모든 양의 정수는 오름차순으로 정렬된 소수들의 곱으로 유일하게 표현된다. 결국 Prime Factorization(소인수분해)를 이야기한다고 볼 수 있다. ) • 1 = (product of empty series) = 1 • 2 = 2 (product of series with one element 2) • 4 = 2· 2 (product of series 2, 2) • 2000 = 2· 2· 5· 5· 5 = 24· 53; 2001 = 3· 29; 2002 = 2· 7· 11· 13; 2003 = 2003 Page 8 Discrete Mathematics by Yang-Sae Moon

The Division “Algorithm” The Integers and Division Really just a theorem, not an algorithm… • The name is used here for historical reasons. For any integer dividend a and divisor d≠ 0, there is a unique integer quotient q and remainder r N such that a = dq + r and 0 r < |d|. • dividend = “피제수”, divisor = “제수” • quotient = “몫”, remainder = “나머지” a, d Z, d>0: !q, r Z: 0 r<|d|, a=dq+r. ( ! means “unique”) We can find q and r by: q= a d , r=a qd. (e. g. , if a = 14 and d = 3, then q = 14 3 = 4 and r = 14 - 3· 4 = 2. Page 10 Discrete Mathematics by Yang-Sae Moon

Greatest Common Divisor (최대공약수) The Integers and Division The greatest common divisor gcd(a, b) of integers a, b (not both 0) is the largest (most positive) integer d that is a divisor both of a and of b. (최대공약수는 두 수의 공약수 중에서 가장 큰 공약수이다. ) d = gcd(a, b) = max(d: d|a d|b) Example: gcd(24, 36)=? Positive common divisors: 1, 2, 3, 4, 6, 12 Greatest is 12. Page 11 Discrete Mathematics by Yang-Sae Moon

GCD shortcut The Integers and Division If the prime factorizations are written as and then the GCD is given by: , Example: • a=84=2· 2· 3· 7 = 22· 31· 71 • b=96=2· 2· 2· 3 = 25· 31· 70 • gcd(84, 96) = 22· 31· 70 = 2· 2· 3 = 12. Page 12 Discrete Mathematics by Yang-Sae Moon

Relatively Primality (서로 소, 상대 소수) The Integers and Division Integers a and b are called relatively prime or coprime iff their gcd = 1. (두 수의 최대공약수가 1인 경우, 두 수는 서로 소(상대 소수)라 한다. ) Example: Neither 21 and 10 are prime, but they are coprime. 21=3· 7 and 10=2· 5, so they have no common factors > 1, so their gcd = 1. A set of integers {a 1, a 2, …} is (pairwise) relatively prime if all pairs ai, aj, i j, are relatively prime. (주어진 정수들의 모든 쌍이 서로 소이면, 해당 정수들은 서로 소라 한다. ) • E. g. , 10, 17, and 21 are relatively primes. Page 13 Discrete Mathematics by Yang-Sae Moon

Least Common Multiple (최소공배수) The Integers and Division lcm(a, b) of positive integers a, b, is the smallest positive integer that is a multiple both of a and of b. m = lcm(a, b) = min(m: a|m b|m) (최소공배수는 두 수의 공배수 중에서 가장 작은 공배수이다. ) • E. g. lcm(6, 10)=30 If the prime factorizations are written as and , then the LCM is given by Page 14 Discrete Mathematics by Yang-Sae Moon

A Useful Rule The Integers and Division If a and b are positive integers, then ab = gcd(a, b)·lcm(a, b) Prove it by yourself! Page 15 Discrete Mathematics by Yang-Sae Moon

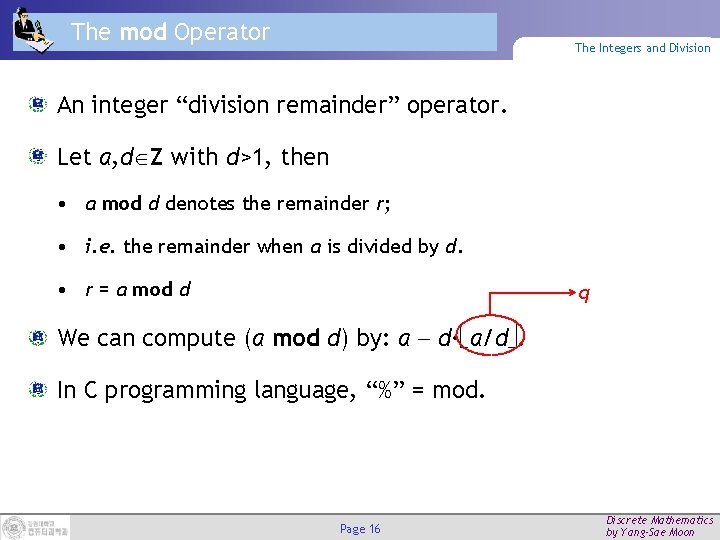
The mod Operator The Integers and Division An integer “division remainder” operator. Let a, d Z with d>1, then • a mod d denotes the remainder r; • i. e. the remainder when a is divided by d. • r = a mod d q We can compute (a mod d) by: a d· a/d. In C programming language, “%” = mod. Page 16 Discrete Mathematics by Yang-Sae Moon

Modular Congruence (모듈로 합동? ) The Integers and Division Let Z+={n Z | n>0}, the positive integers. Let a, b Z, m Z+. Then a is congruent to b modulo m, written “a b(mod m)”, iff m|(a b). Also equivalent to: (a b) mod m = 0. • m으로 나누었을 때, a와 b의 나머지가 동일(합동)하다. • m으로 나누어 나머지가 동일한 수의 차를 m으로 나누면 나머지가 0이다. 두 수의 차를 m으로 나눌 수 있으면, 두 수를 m으로 나눈 나머지는 동일하다. Example: 17 5(mod 6) 6|(17– 5), (17– 5)%6 = 0 Page 17 Discrete Mathematics by Yang-Sae Moon

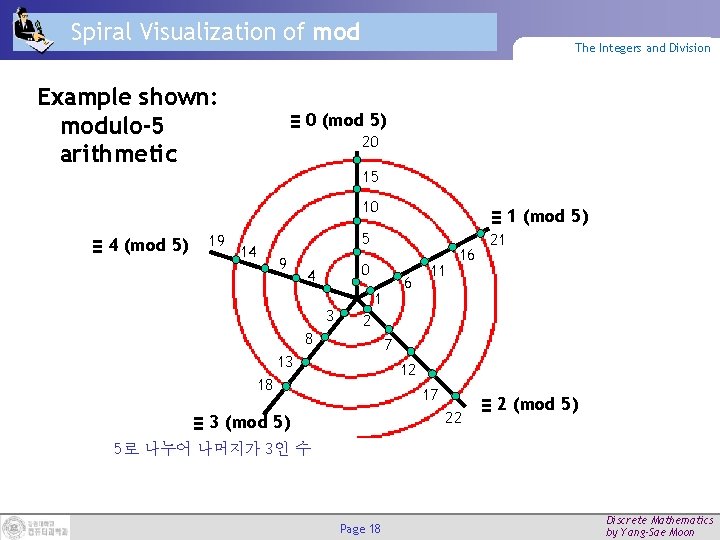
Spiral Visualization of mod Example shown: modulo-5 arithmetic The Integers and Division ≡ 0 (mod 5) 20 15 10 ≡ 4 (mod 5) 19 14 ≡ 1 (mod 5) 5 9 0 4 3 8 6 1 11 16 21 2 7 13 12 18 17 22 ≡ 3 (mod 5) ≡ 2 (mod 5) 5로 나누어 나머지가 3인 수 Page 18 Discrete Mathematics by Yang-Sae Moon

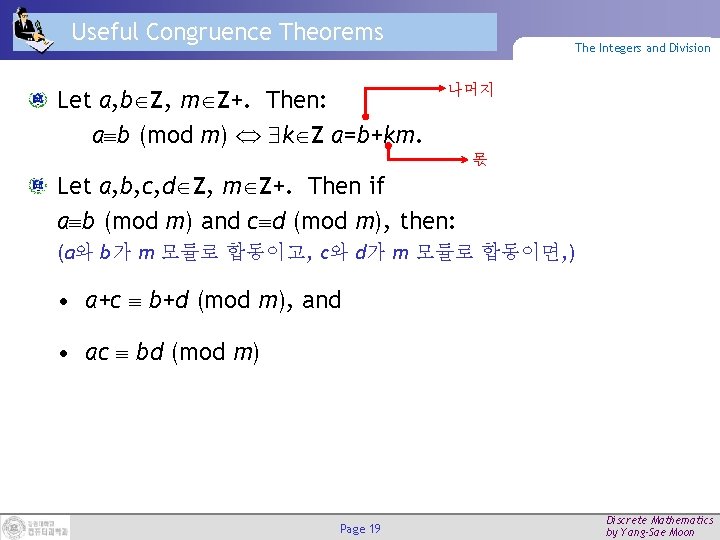
Useful Congruence Theorems Let a, b Z, m Z+. Then: a b (mod m) k Z a=b+km. The Integers and Division 나머지 몫 Let a, b, c, d Z, m Z+. Then if a b (mod m) and c d (mod m), then: (a와 b가 m 모듈로 합동이고, c와 d가 m 모듈로 합동이면, ) • a+c b+d (mod m), and • ac bd (mod m) Page 19 Discrete Mathematics by Yang-Sae Moon

Applications of Congruence (합동의 응용) The Integers and Division The mod operator is widely used in hash functions. • h(key) = key mod m Linear congruential methods is used to generate pseudo random numbers. • x[n+1] = (a·x[n] + c) mod m (생략) Also, in cryptography, encryption, … Page 20 Discrete Mathematics by Yang-Sae Moon

강의 내용 Integers and Algorithms 정수와 나눗셈(The Integers and Division) 정수와 알고리즘(Integers and Algorithms) Page 21 Discrete Mathematics by Yang-Sae Moon

Introduction Integers and Algorithms Base-b representations of integers. (b진법 표현) • Especially: binary, hexadecimal, octal. • Also, two’s complement representation (2의 보수 표현) Algorithms for computer arithmetic: • Binary addition, multiplication, division. Euclidean algorithm for finding GCD’s. Page 22 Discrete Mathematics by Yang-Sae Moon

Base-b Representations of Integers and Algorithms If b is a positive integer greater than 1, then a given positive integer n can be uniquely represented as follows: n = akbk + ak-1 bk-1 + … + a 1 b 1 + a 0 b 0 where • k is a natural number. • and a 0, a 1, …, and ak are natural numbers less than b. • ak 0. Example: • 165 = 1· 102 + 6· 101 + 5· 100 = (165)10 • 165 = 2· 82 + 4· 81 + 5· 80 = (245)8 Page 23 Discrete Mathematics by Yang-Sae Moon

Base-b Number Systems Integers and Algorithms Ordinarily we write base-10 representations of numbers (using digits 0 -9). However, 10 isn’t special; any base b>1 will work. For any positive integers n, b, there is a unique sequence akak-1… a 1 a 0 of digits ai<b such that The “base b expansion of n” (n의 밑수 b 전개, n의 b진법 표현) Page 24 Discrete Mathematics by Yang-Sae Moon

Particular Bases of Interest Integers and Algorithms Used only because we have 10 fingers Base b=10 (decimal): 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Used internally in all modern computers Base b=2 (binary): 2 digits: 0, 1. (“Bits”=“binary digits. ”) Octal digits correspond to groups of 3 bits Base b=8 (octal): 8 digits: 0, 1, 2, 3, 4, 5, 6, 7. Hex digits give groups of 4 bits Base b=16 (hexadecimal): 16 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Page 25 Discrete Mathematics by Yang-Sae Moon

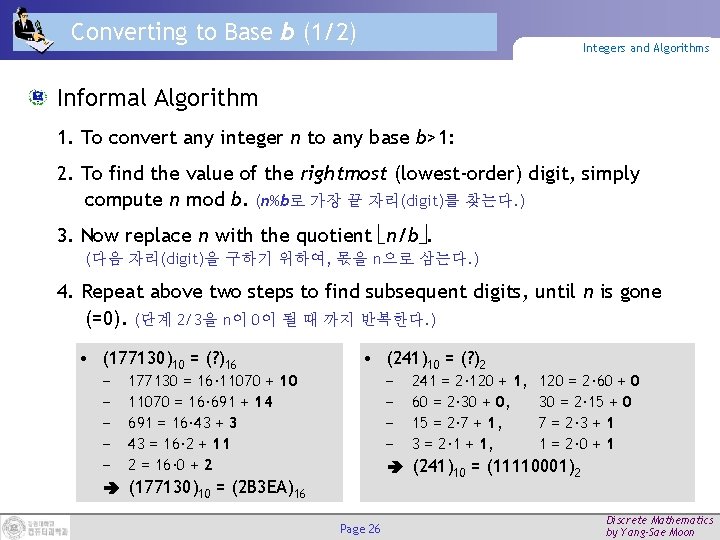
Converting to Base b (1/2) Integers and Algorithms Informal Algorithm 1. To convert any integer n to any base b>1: 2. To find the value of the rightmost (lowest-order) digit, simply compute n mod b. (n%b로 가장 끝 자리(digit)를 찾는다. ) 3. Now replace n with the quotient n/b. (다음 자리(digit)을 구하기 위하여, 몫을 n으로 삼는다. ) 4. Repeat above two steps to find subsequent digits, until n is gone (=0). (단계 2/3을 n이 0이 될 때 까지 반복한다. ) • (177130)10 = (? )16 − − − 177130 = 16· 11070 + 10 11070 = 16· 691 + 14 691 = 16· 43 + 3 43 = 16· 2 + 11 2 = 16· 0 + 2 • (241)10 = (? )2 − − (177130)10 = (2 B 3 EA)16 Page 26 241 = 2· 120 + 1, 60 = 2· 30 + 0, 15 = 2· 7 + 1, 3 = 2· 1 + 1, 120 = 2· 60 + 0 30 = 2· 15 + 0 7 = 2· 3 + 1 1 = 2· 0 + 1 (241)10 = (11110001)2 Discrete Mathematics by Yang-Sae Moon

Converting to Base b (2/2) Integers and Algorithms Formal Algorithm procedure base b expansion (n: positive integer) q : = n k : = 0 while q 0 begin ak : = q mod b {remainder} q : = q/b {quotient} k : = k + 1 end {the base b expansion of n is (akak-1… a 1 a 0)b} Page 27 Discrete Mathematics by Yang-Sae Moon

Addition of Binary Numbers Integers and Algorithms Intuition (let a = (an-1… a 1 a 0)2, b = (bn-1… b 1 b 0)2) = = . . c 1 c 0 a 2 a 1 a 0 b 2 b 1 b 0 ci = (ai-1+bi-1+ci-1)/2 a b cn-1 cn-2 an-1 an-2 bn-1 bn-2 a+b = sn sn-1 sn-2 . . . s 2 s 1 s 0 si = (ai+bi+ci)%2 Algorithm procedure add(an− 1…a 0, bn− 1…b 0: binary expressions of a, b) c : = 0 {c mean a carry} for i : = 0 to n− 1 {i means a bit index} begin sum : = ai + bi + c {2 -bit sum} si : = sum mod 2 {low bit of sum} c : = sum/2 {high bit of sum} end sn : = c {the binary expression of the sum is (snsn-1… s 1 s 0)2} Page 28 O(n) Discrete Mathematics by Yang-Sae Moon

2’s Complement (2의 보수) (1/2) Integers and Algorithms In binary, negative numbers can be conveniently represented using 2’s complement notation. (실제로, 컴퓨터에서는 음수를 2의 보수로 표현한다. ) In this scheme, a string of n bits can represent integers − 2 n− 1 ~ (2 n− 1− 1). • 0이상의 정수만 표현한다면… 0 ~ 2 n− 1 (unsigned int n) • 음의 정수까지 표현한다면… − 2 n-1 ~ 2 n-1− 1 (int n) The bit in the highest-order bit-position (n− 1) represents a coefficient multiplying − 2 n− 1; (왼쪽 첫 번째 bit는 “ − 2 n− 1”을 나타내며, 흔히 부호(+ or −)를 의미한다. ) • The other positions i < n− 1 just represent 2 i, as before. Page 29 Discrete Mathematics by Yang-Sae Moon

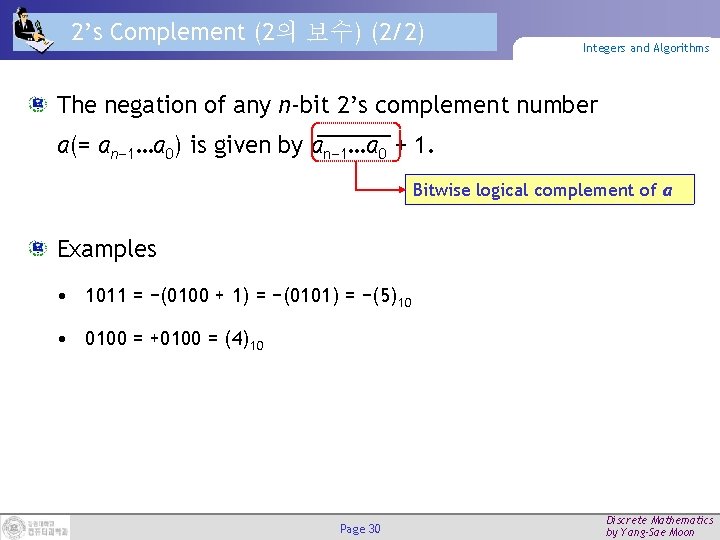
2’s Complement (2의 보수) (2/2) Integers and Algorithms The negation of any n-bit 2’s complement number a(= an− 1…a 0) is given by an− 1…a 0 + 1. Bitwise logical complement of a Examples • 1011 = −(0100 + 1) = −(0101) = −(5)10 • 0100 = +0100 = (4)10 Page 30 Discrete Mathematics by Yang-Sae Moon

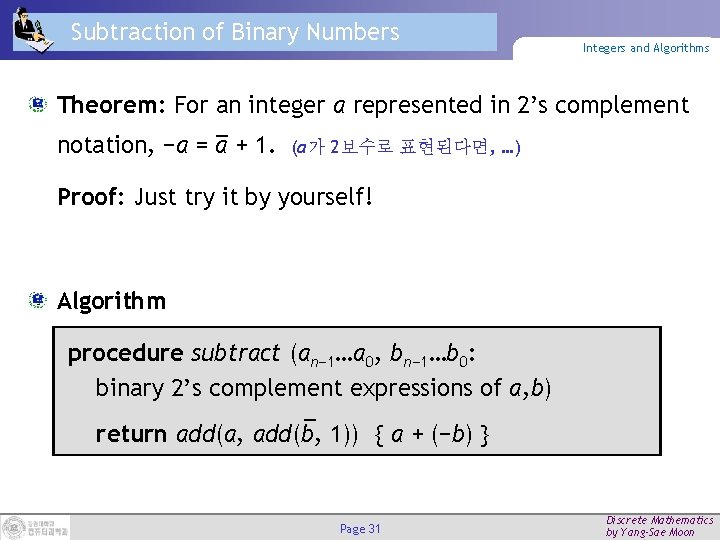
Subtraction of Binary Numbers Integers and Algorithms Theorem: For an integer a represented in 2’s complement notation, −a = a + 1. (a가 2보수로 표현된다면, …) Proof: Just try it by yourself! Algorithm procedure subtract (an− 1…a 0, bn− 1…b 0: binary 2’s complement expressions of a, b) return add(a, add(b, 1)) { a + (−b) } Page 31 Discrete Mathematics by Yang-Sae Moon

Multiplication of Binary Numbers (1/2) Integers and Algorithms Intuition (let a = (an-1… a 1 a 0)2, b = (bn-1… b 1 b 0)2) +) a b c 0 c 1 c 2 = = = a·b = cn-1 an-2. . . bn-1 bn-2. . . s(n-1, 0)s(n-2, 0). . . s(n-1, 1)s(n-2, 1). . . s(2, 1) s(n-1, 2)s(n-2, 2). . . s(2, 2). . . + cn-2 +. . . + c 2 + c 1 + c 0 a 2 b 2 s(2, 0) s(1, 1) s(1, 2) a 1 b 1 s(1, 0) s(0, 1) s(0, 2) a 0 b 0 s(0, 0) 0 0 0 s(i, j) = (if bj = 1 then ai else 0) cj = (if bj = 1 then a << j else 0) Page 32 Discrete Mathematics by Yang-Sae Moon

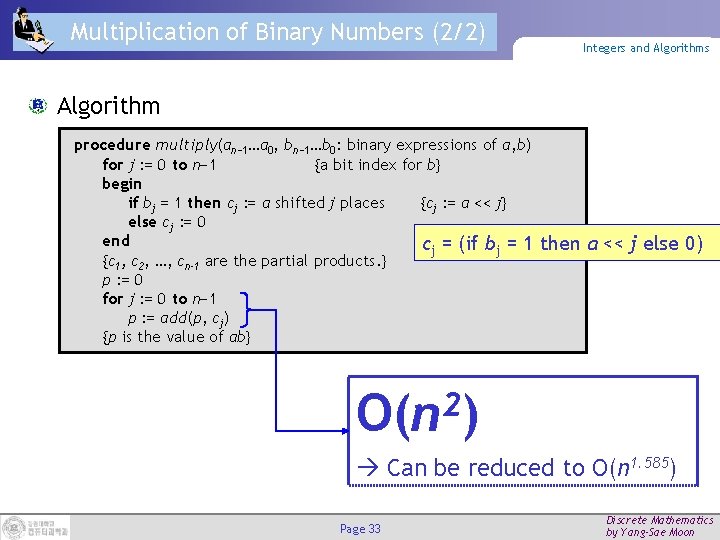
Multiplication of Binary Numbers (2/2) Integers and Algorithms Algorithm procedure multiply(an− 1…a 0, bn− 1…b 0: binary expressions of a, b) for j : = 0 to n− 1 {a bit index for b} begin if bj = 1 then cj : = a shifted j places {cj : = a << j} else cj : = 0 end cj = (if bj = 1 {c 1, c 2, …, cn-1 are the partial products. } p : = 0 for j : = 0 to n− 1 p : = add(p, cj) {p is the value of ab} then a << j else 0) 2 O(n ) Can be reduced to O(n 1. 585) Page 33 Discrete Mathematics by Yang-Sae Moon

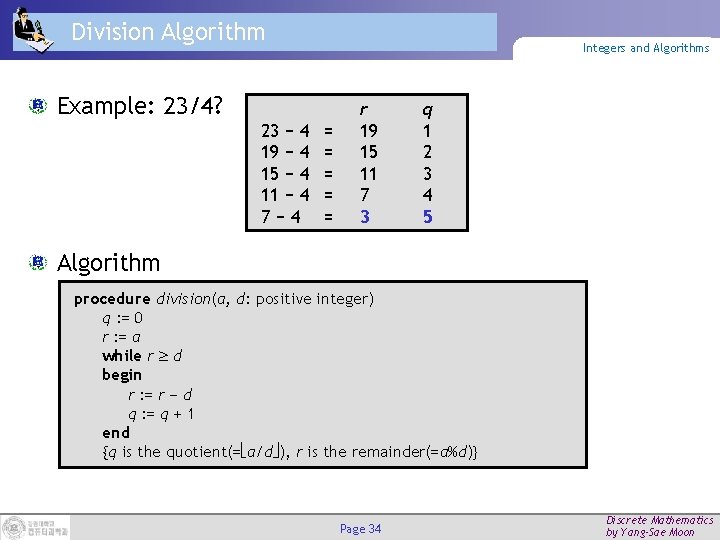
Division Algorithm Integers and Algorithms Example: 23/4? 23 − 4 19 − 4 15 − 4 11 − 4 7− 4 = = = r 19 15 11 7 3 q 1 2 3 4 5 Algorithm procedure division(a, d: positive integer) q : = 0 r : = a while r d begin r : = r − d q : = q + 1 end {q is the quotient(= a/d ), r is the remainder(=a%d)} Page 34 Discrete Mathematics by Yang-Sae Moon

Euclid’s Algorithm for GCD Integers and Algorithms Finding GCDs by comparing prime factorizations can be difficult if the prime factors are unknown. (소인수분해로 최대공약수를 구하는 것은 어렵다. 특히, 큰 수인 경우…) Euclid discovered: For all integers a, b, gcd(a, b) = gcd((a mod b), b). Sort a, b so that a>b, and then (given b>1) (a mod b) < a, so problem is simplified. Examples • gcd(372, 164) = gcd(372 mod 164, 164) [372%164 = 44] • gcd(164, 44) = gcd(164 mod 44, 44) [164%44 = 32] • gcd(44, 32) = gcd(44 mod 32, 32) = gcd(12, 8) gcd(8, 4) = gcd(4, 0) = 4. Page 35 Discrete Mathematics by Yang-Sae Moon

Euclid’s Algorithms Integers and Algorithms Algorithm in Pseudocode procedure gcd(a, b: positive integer) while b 0 begin r : = a mod b {r = a % b} a : = b b : = r end return a Algorithm in C (using recursive calls) int gcd(int a, int b) /* assume a > b */ { if(b==0) return a; else return gcd(b, a%b); } Page 37 Discrete Mathematics by Yang-Sae Moon

강의 내용 Integers and Algorithms 정수와 나눗셈(The Integers and Division) 정수와 알고리즘(Integers and Algorithms) Page 38 Discrete Mathematics by Yang-Sae Moon