Integers and Algorithms The Integers and Division Integers

강의 내용 Integers and Algorithms 정수와 나눗셈(The Integers and Division) 정수와 알고리즘(Integers and Algorithms) Page 2 Computer Algorithms by Yang-Sae Moon

나누기(divides), 인수(factor), 배수(multiple) The Integers and Division Let a, b Z with a 0. (a, b가 정수라 하자) a|b “a divides b” : “ c Z: b=ac” “There is an integer c such that c times a equals b. ” (b가 a로 나누어짐(a로 b를 나눌 수 있음)을 의미하며, 이때 몫이 c이다. ) • 예제: 3 12 True, but 3 7 False. 인수 If a divides b, then we say a is a factor or a divisor of b, and b is a multiple of a. 배수 “b is even(짝수)” : ≡ 2 b. Is 0 even? Is − 4? Page 4 Computer Algorithms by Yang-Sae Moon

Prime Numbers (소수) The Integers and Division 정수 p(>1)가 소수(prime)라면 p는 1보다 큰 어떤 두 정수의 곱으 로 나타낼 수 없다. (An integer p>1 is prime iff it is not the product of any two integers greater than 1. ) p>1 a, b N: a>1, b>1, ab=p. 즉, 양의 인수(factors)가 1과 p 자신 뿐이면, p를 소수라 한다. 소수의 예: 2, 3, 5, 7, 11, 13. . . 비소수(non-prime)을 합성수(composite)라 한다. 합성수라 하는 이유는 다른 두 정수의 곱으로 합성되기 때문이다. Page 7 Computer Algorithms by Yang-Sae Moon

Fundamental Theorem of Arithmetic (산술의 기본 정리) The Integers and Division 정리: 모든 양의 정수는 오름차순으로 정렬된 소수들의 곱으로 유 일하게 표현된다. 결국 Prime Factorization(소인수분해)를 이야기한다고 볼 수 있다. • 1 = (product of empty series) = 1 • 2 = 2 (product of series with one element 2) • 4 = 2· 2 (product of series 2, 2) • 2000 = 2· 2· 5· 5· 5 = 24· 53; 2001 = 3· 29; 2002 = 2· 7· 11· 13; 2003 = 2003; . . . ; 2020 = ? ; 2021 = ? Page 8 Computer Algorithms by Yang-Sae Moon

Greatest Common Divisor (최대공약수) The Integers and Division 정수 a, b의 최대공약수 gcd(a, b)는 두 수의 공약수 중에서 가장 큰 공약수이다. d = gcd(a, b) = max(d: d|a d|b) 예제: gcd(24, 36)=? • 양의 공약수: 1, 2, 3, 4, 6, 12 • 최대공약수 = 12 Page 11 Computer Algorithms by Yang-Sae Moon

유용한 규칙 The Integers and Division 두 양의 정수 a, b에 대해 다음 관계가 성립한다. ab = gcd(a, b)·lcm(a, b) Prove it by yourself! Page 15 Computer Algorithms by Yang-Sae Moon

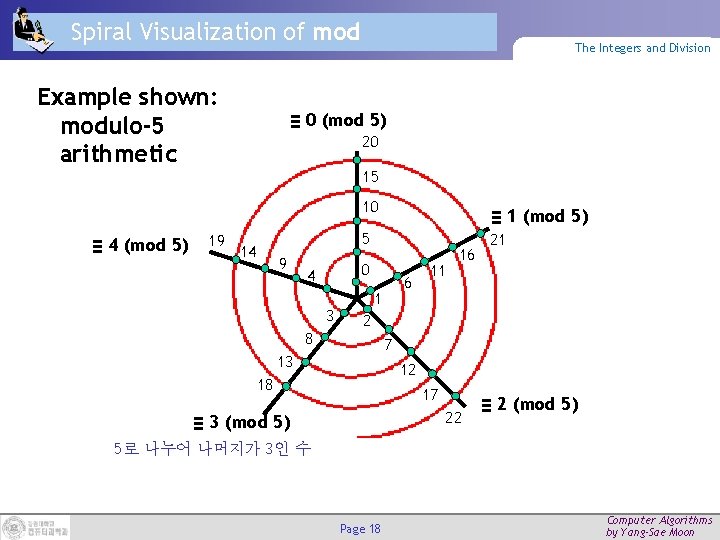
Spiral Visualization of mod Example shown: modulo-5 arithmetic The Integers and Division ≡ 0 (mod 5) 20 15 10 ≡ 4 (mod 5) 19 14 ≡ 1 (mod 5) 5 9 0 4 3 8 6 1 11 16 21 2 7 13 12 18 17 22 ≡ 3 (mod 5) ≡ 2 (mod 5) 5로 나누어 나머지가 3인 수 Page 18 Computer Algorithms by Yang-Sae Moon

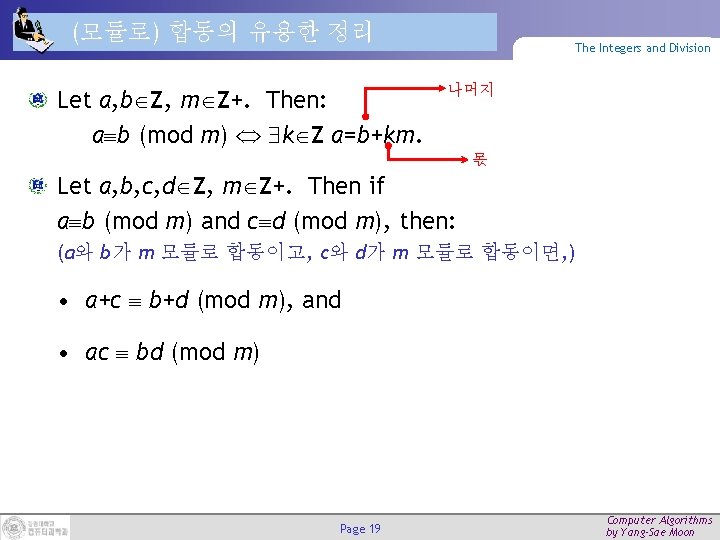
(모듈로) 합동의 유용한 정리 Let a, b Z, m Z+. Then: a b (mod m) k Z a=b+km. The Integers and Division 나머지 몫 Let a, b, c, d Z, m Z+. Then if a b (mod m) and c d (mod m), then: (a와 b가 m 모듈로 합동이고, c와 d가 m 모듈로 합동이면, ) • a+c b+d (mod m), and • ac bd (mod m) Page 19 Computer Algorithms by Yang-Sae Moon

Applications of Congruence (합동의 응용) The Integers and Division 나머지(mod) 연산자는 해시 함수(hash functions)에서 널리 사용 된다. • h(key) = key mod m 모듈로 합동 연산은 유사 랜덤 넘버(pseudo random numbers) 생 성에 사용된다. • x[n+1] = (a·x[n] + c) mod m (생략) 또한, 암호(cryptography), 부호화(encryption) 등에서도 널리 사용된다. Page 20 Computer Algorithms by Yang-Sae Moon

강의 내용 Integers and Algorithms 정수와 나눗셈(The Integers and Division) 정수와 알고리즘(Integers and Algorithms) Page 21 Computer Algorithms by Yang-Sae Moon

개요 Integers and Algorithms 정수의 b-진법 표현 • 특히, 이진수(binary), 16진수(hexadecimal), 8진수(octal) • 또한, 2의 보수(two’s complement) 표현 컴퓨터 연산에서의 정수 알고리즘 • 이진수 덧셈(addition), 곱셈(multiplication), 나눗셈(division) 최대공약수(GCD) 계산을 위한 유클리드(Euclid) 알고리즘 Page 22 Computer Algorithms by Yang-Sae Moon

Particular Bases of Interest Base b=10 (decimal, 십진수): Integers and Algorithms Used only because we have 10 fingers 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Used internally in all modern computers Base b=2 (binary, 이진수): 2 digits: 0, 1. (“Bits”=“binary digits. ”) Octal digits correspond to groups of 3 bits Base b=8 (octal, 8진수): 8 digits: 0, 1, 2, 3, 4, 5, 6, 7. Base b=16 (hexadecimal, 16진수): Hex digits give groups of 4 bits 16 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Page 25 Computer Algorithms by Yang-Sae Moon

진법 변환[Converting to Base b] (1/2) Integers and Algorithms 개략적 알고리즘 (Informal Algorithm) 1. 임의의 정수 n을 b-진법으로 변환하기 위해서는: 2. (n mod b)를 사용하여 가장 끝 자리(digit) 숫자를 찾는다. (n%b 사용) 3. 다음 자리(digit)를 구하기 위해 몫( n/b )을 n으로 삼는다. 4. 단계 2와 3을 n이 0이 될 때까지 반복한다. • (177130)10 = (? )16 − 177130 = 16· 11070 + 10 − 11070 = 16· 691 + 14 − 691 = 16· 43 + 3 − 43 = 16· 2 + 11 − 2 = 16· 0 + 2 (177130)10 = (2 B 3 EA)16 • (241)10 = (? )2 − 241 = 2· 120 + 1, 120 = 2· 60 + 0 − 60 = 2· 30 + 0, 30 = 2· 15 + 0 − 15 = 2· 7 + 1, 7 = 2· 3 + 1 − 3 = 2· 1 + 1, 1 = 2· 0 + 1 (241)10 = (11110001)2 Page 26 Computer Algorithms by Yang-Sae Moon

진법 변환[Converting to Base b] (2/2) Integers and Algorithms 정형적 알고리즘(Formal Algorithm) procedure base b expansion (n: positive integer) q : = n k : = 0 while q 0 begin ak : = q mod b {remainder} q : = q/b {quotient} k : = k + 1 end {the base b expansion of n is (akak-1… a 1 a 0)b} Page 27 Computer Algorithms by Yang-Sae Moon

이진수 덧셈(Addition of Binary Numbers) Integers and Algorithms 직관 (let a = (an-1… a 1 a 0)2, b = (bn-1… b 1 b 0)2) = = . . c 1 c 0 a 2 a 1 a 0 b 2 b 1 b 0 ci = (ai-1+bi-1+ci-1)/2 a b cn-1 cn-2 an-1 an-2 bn-1 bn-2 a+b = sn sn-1 sn-2 . . . s 2 s 1 s 0 si = (ai+bi+ci)%2 알고리즘 procedure add(an− 1…a 0, bn− 1…b 0: binary expressions of a, b) c : = 0 {c mean a carry} for i : = 0 to n− 1 {i means a bit index} begin sum : = ai + bi + c {2 -bit sum} si : = sum mod 2 {low bit of sum} c : = sum/2 {high bit of sum} end sn : = c {the binary expression of the sum is (snsn-1… s 1 s 0)2} Page 28 O(n) Computer Algorithms by Yang-Sae Moon

2의 보수[2’s Complement] (2/2) Integers and Algorithms 임의의 n-비트 정수 a(= an− 1…a 0)의 2의 보수는 다음과 같다. an− 1…a 0 + 1 Bitwise logical complement of a 예제: • 1011 = −(0100 + 1) = −(0101) = −(5)10 • 0100 = +0100 = (4)10 Page 30 Computer Algorithms by Yang-Sae Moon

이진수 뺄셈(Subtraction of Binary Numbers) Integers and Algorithms 정리: 정수 a가 2의 보수로 표현된다면 다음이 성립한다. −a = a + 1 증명: Just try it by yourself! 뺄셈 알고리즘 procedure subtract (an− 1…a 0, bn− 1…b 0: binary 2’s complement expressions of a, b) return add(a, add(b, 1)) { a + (−b) } Page 31 Computer Algorithms by Yang-Sae Moon

이진수 곱셉[Multiplication of Binary Numbers] (1/2) Integers and Algorithms 직관 (let a = (an-1… a 1 a 0)2, b = (bn-1… b 1 b 0)2) +) a b c 0 c 1 c 2 = = = a·b = cn-1 an-2. . . bn-1 bn-2. . . s(n-1, 0)s(n-2, 0). . . s(n-1, 1)s(n-2, 1). . . s(2, 1) s(n-1, 2)s(n-2, 2). . . s(2, 2). . . + cn-2 +. . . + c 2 + c 1 + c 0 a 2 b 2 s(2, 0) s(1, 1) s(1, 2) a 1 b 1 s(1, 0) s(0, 1) s(0, 2) a 0 b 0 s(0, 0) 0 0 0 s(i, j) = (if bj = 1 then ai else 0) cj = (if bj = 1 then a << j else 0) Page 32 Computer Algorithms by Yang-Sae Moon

이진수 곱셉[Multiplication of Binary Numbers] (2/2) Integers and Algorithms 알고리즘 procedure multiply(an− 1…a 0, bn− 1…b 0: binary expressions of a, b) for j : = 0 to n− 1 {a bit index for b} begin if bj = 1 then cj : = a shifted j places {cj : = a << j} else cj : = 0 end cj = (if bj = 1 {c 1, c 2, …, cn-1 are the partial products. } p : = 0 for j : = 0 to n− 1 p : = add(p, cj) {p is the value of ab} then a << j else 0) 2 O(n ) Can be reduced to O(n 1. 585) Page 33 Computer Algorithms by Yang-Sae Moon

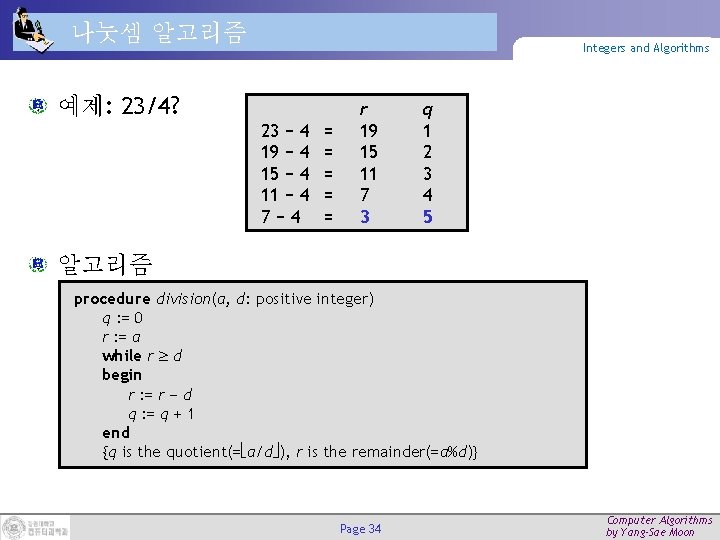
나눗셈 알고리즘 Integers and Algorithms 예제: 23/4? 23 − 4 19 − 4 15 − 4 11 − 4 7− 4 = = = r 19 15 11 7 3 q 1 2 3 4 5 알고리즘 procedure division(a, d: positive integer) q : = 0 r : = a while r d begin r : = r − d q : = q + 1 end {q is the quotient(= a/d ), r is the remainder(=a%d)} Page 34 Computer Algorithms by Yang-Sae Moon

유클리드 알고리즘 코드 Integers and Algorithms Algorithm in Pseudocode procedure gcd(a, b: positive integer) while b 0 begin r : = a mod b {r = a % b} a : = b b : = r end return a Algorithm in C (using recursive calls) int gcd(int a, int b) /* assume a > b */ { if(b==0) return a; else return gcd(b, a%b); } Page 37 Computer Algorithms by Yang-Sae Moon

강의 내용 Integers and Algorithms 정수와 나눗셈(The Integers and Division) 정수와 알고리즘(Integers and Algorithms) Page 38 Computer Algorithms by Yang-Sae Moon