CSCE 715 Network Systems Security ChinTser Huang huangctcse













































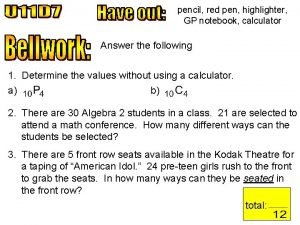
- Slides: 45

CSCE 715: Network Systems Security Chin-Tser Huang huangct@cse. sc. edu University of South Carolina 01/28/2009

After DES… n More symmetric encryption algorithms n n Triple-DES Advanced Encryption Standards 01/28/2009 2

Triple DES n Clearly a replacement for DES was needed n n theoretical attacks that can break it demonstrated exhaustive key search attacks Use multiple encryptions with DES implementations Triple-DES is the chosen form 01/28/2009 3

Why Triple-DES? n Double-DES may suffer from meet-in-themiddle attack n n n works whenever use a cipher twice assume C = EK 2[EK 1[P]], so X = EK 1[P] = DK 2[C] given a known pair (P, C), attack by encrypting P with all keys and store then decrypt C with keys and match X value can be shown that this attack takes O(256) steps 01/28/2009 4

Triple-DES with Two Keys n Must use 3 encryptions n n But can use 2 keys with E-D-E sequence n n n would seem to need 3 distinct keys encrypt & decrypt equivalent in security C = EK 1[DK 2[EK 1[P]]] if K 1=K 2 then can work with single DES Standardized in ANSI X 9. 17 & ISO 8732 No current known practical attacks 01/28/2009 5

Triple-DES with Three Keys n n Some proposed attacks on two-key Triple-DES, although none of them practical Can use Triple-DES with Three-Keys to avoid even these n n C = EK 3[DK 2[EK 1[P]]] Has been adopted by some Internet applications, e. g. PGP, S/MIME 01/28/2009 6

Origins of Advanced Encryption Standard n n n Triple-DES is slow with small blocks US NIST issued call for ciphers in 1997 15 candidates accepted in Jun 1998 5 were shortlisted in Aug 1999 Rijndael was selected as the AES in Oct 2000 Issued as FIPS PUB 197 standard in Nov 2001 01/28/2009 7

AES Requirements n n n n Private key symmetric block cipher 128 -bit data, 128/192/256 -bit keys Stronger and faster than Triple-DES Active life of 20 -30 years (+ archival use) Provide full specification and design details Both C and Java implementations NIST has released all submissions and unclassified analyses 01/28/2009 8

AES Evaluation Criteria n Initial criteria n n security – effort to practically cryptanalyze cost – computational algorithm & implementation characteristics Final criteria n n general security software & hardware implementation ease implementation attacks flexibility (in en/decrypt, keying, other factors) 01/28/2009 9

AES Shortlist n Shortlist in Aug 99 after testing and evaluation n n n MARS (IBM) - complex, fast, high security margin RC 6 (USA) - very simple, very fast, low security margin Rijndael (Belgium) - clean, fast, good security margin Serpent (Euro) - slow, clean, very high security margin Twofish (USA) - complex, very fast, high security margin Subject to further analysis and comment Contrast between algorithms with n n few complex rounds verses many simple rounds refined existing ciphers verses new proposals 01/28/2009 10

The Winner - Rijndael n n n Designed by Rijmen-Daemen in Belgium Has 128/192/256 bit keys, 128 bit data An iterative rather than feistel cipher n n n Designed to be n n treats data in 4 groups of 4 bytes operates an entire block in every round resistant against known attacks speed and code compactness on many CPUs design simplicity Use finite field 01/28/2009 11

Abstract Algebra Background n n n Group Ring Field 01/28/2009 12

Group n n n A set of elements or “numbers” With a binary operation whose result is also in the set (closure) Obey following axioms n n associative law: has identity e: has inverses a-1: (a. b). c = a. (b. c) e. a = a. e = a a. a-1 = e Abelian group if commutative a. b = b. a 01/28/2009 13

Ring n n n A set of elements with two operations (addition and multiplication) which are: an abelian group with addition operation multiplication n n has closure is associative distributive over addition: a(b+c) = ab + ac Commutative ring if multiplication operation is commutative Integral domain if multiplication operation has identity and no zero divisors 01/28/2009 14

Field n n n A set of numbers with two operations n integral domain n multiplicative inverse: aa-1 = a-1 a= 1 Infinite field if infinite number of elements Finite field if finite number of elements 01/28/2009 15

Modular Arithmetic n n Define modulo operator a mod n to be remainder when a is divided by n Use the term congruence for: a ≡ b mod n when divided by n, a and b have same remainder n e. g. 100 34 mod 11 b is called the residue of a mod n if 0 b n-1 n with integers can write a = qn + b n n 01/28/2009 16

Divisor n A non-zero number b is a divisor of a if for some m have a=mb (a, b, m all integers) That is, b divides a with no remainder Denote as b|a n E. g. all of 1, 2, 3, 4, 6, 8, 12, 24 divide 24 n n 01/28/2009 17

Modular Arithmetic n n Can do modular arithmetic with any group of integers Zn = {0, 1, … , n-1} Form a commutative ring for addition With a multiplicative identity Some peculiarities n n if (a+b)≡(a+c) mod n then b≡c mod n but (ab)≡(ac) mod n then b≡c mod n only if a is relatively prime to n 01/28/2009 18

Modulo 8 Example 01/28/2009 19

Greatest Common Divisor (GCD) n GCD (a, b) of a and b is the largest number that divides evenly into both a and b n n e. g. GCD(60, 24) = 12 Two numbers are called relatively prime if they have no common factors (except 1) n e. g. 8 and 15 relatively prime as GCD(8, 15) = 1 01/28/2009 20

Euclid's GCD Algorithm n Use following theorem n n GCD(a, b) = GCD(b, a mod b) Euclid's Algorithm to compute GCD(a, b) n n A=a, B=b while B>0 n n n R = A mod B A = B, B = R return A 01/28/2009 21

Galois Fields n n n Finite fields play a key role in cryptography Number of elements in a finite field must be a power of a prime pn Known as Galois fields Denoted GF(pn) In particular often use the following forms n n GF(p) GF(2 n) 01/28/2009 22

Galois Fields GF(p) n n GF(p) is set of integers {0, 1, … , p-1} with arithmetic operations modulo prime p Form a finite field n n have multiplicative inverses Hence arithmetic is “well-behaved” and can do addition, subtraction, multiplication, and division without leaving the field GF(p) 01/28/2009 23

Arithmetic in GF(7) 01/28/2009 24

Finding Multiplicative Inverses n By extending Euclid’s algorithm 1. (A 1, A 2, A 3)=(1, 0, m); (B 1, B 2, B 3)=(0, 1, b) 2. if B 3 = 0 return A 3 = gcd(m, b); no inverse 3. if B 3 = 1 return B 3 = gcd(m, b); B 2 = b– 1 mod m 4. Q = A 3 div B 3 5. (T 1, T 2, T 3)=(A 1 – Q B 1, A 2 – Q B 2, A 3 – Q B 3) 6. (A 1, A 2, A 3)=(B 1, B 2, B 3) 7. (B 1, B 2, B 3)=(T 1, T 2, T 3) 8. goto 2 01/28/2009 25

Polynomial Arithmetic n Can compute using polynomials n Several alternatives available n n n ordinary polynomial arithmetic poly arithmetic with coords mod p and polynomials mod M(x) 01/28/2009 26

Ordinary Polynomial Arithmetic n n n Add or subtract corresponding coefficients Multiply all terms by each other E. g. let f(x) = x 3 + x 2 + 2 and g(x) = x 2 – x + 1 f ( x) + g ( x) = x 3 + 2 x 2 – x + 3 f ( x) – g ( x) = x 3 + x + 1 f ( x) x g ( x) = x 5 + 3 x 2 – 2 x + 2 01/28/2009 27

Polynomial Arithmetic with Modulo Coefficients n n n Compute value of each coefficient as modulo some value Could be modulo any prime But we are most interested in mod 2 i. e. all coefficients are 0 or 1 3 2, g(x) = x 2 + x + 1 n e. g. let f(x) = x + x f ( x) + g ( x) = x 3 + x + 1 f ( x) x g ( x) = x 5 + x 2 n 01/28/2009 28

Modular Polynomial Arithmetic n Can write any polynomial in the form n n n f ( x) = q ( x) g ( x) + r ( x) can interpret r(x) as being a remainder r(x) = f(x) mod g(x) If no remainder say g(x) divides f(x) If g(x) has no divisors other than itself and 1 say it is irreducible (or prime) polynomial Arithmetic modulo an irreducible polynomial forms a field 01/28/2009 29

Polynomial GCD n Can find greatest common divisor for polys n c(x) = GCD(a(x), b(x)) if c(x) is the poly of greatest degree which divides both a(x), b(x) n can adapt Euclid’s Algorithm to find it: n EUCLID[a(x), b(x)] 1. A(x) = a(x); B(x) = b(x) 2. if B(x) = 0 return A(x) = gcd[a(x), b(x)] 3. R(x) = A(x) mod B(x) 4. A(x) B(x) 5. B(x) R(x) 6. goto 2 01/28/2009 30

Modular Polynomial Arithmetic n Can compute in field GF(2 n) n n n polynomials with coefficients modulo 2 whose degree is less than n hence must reduce modulo an irreducible poly of degree n (for multiplication only) Form a finite field Can always find an inverse n can extend Euclid’s Inverse algorithm to find 01/28/2009 31

Arithmetic in GF(23) 01/28/2009 32

AES Cipher – Rijndael n n Process data as 4 groups of 4 bytes (State) Has 9/11/13 rounds in which state undergoes: n n n byte substitution (1 S-box used on every byte) shift rows (permute bytes between groups/columns) mix columns (subs using matrix multiply of groups) add round key (XOR state with key material) Initial XOR key material & incomplete last round All operations can be combined into XOR and table lookups, hence very fast and efficient 01/28/2009 33

AES Encryption and Decryption 01/28/2009 34

AES Data Structure 01/28/2009 35

AES Encryption Round 01/28/2009 36

Byte Substitution n A simple substitution of each byte Uses one table of 16 x 16 bytes containing a permutation of all 256 8 -bit values Each byte of state is replaced by byte in corresponding row (left 4 bits) and column (right 4 bits) n n eg. byte {95} is replaced by row 9 col 5 byte, which is {2 A} S-box is constructed using a defined transformation of the values in GF(28) 01/28/2009 37

Shift Rows n Circular byte shift in each row n n n 1 st row is unchanged 2 nd row does 1 byte circular shift to left 3 rd row does 2 byte circular shift to left 4 th row does 3 byte circular shift to left Decryption does shifts to right Since state is processed by columns, this step permutes bytes between the columns 01/28/2009 38

Mix Columns n n n Each column is processed separately Each byte is replaced by a value dependent on all 4 bytes in the column Effectively a matrix multiplication in GF(28) using prime poly m(x) =x 8+x 4+x 3+x+1 01/28/2009 39

Add Round Key n n XOR state with 128 bits of the round key Again processed by column (though effectively a series of byte operations) Inverse for decryption is identical since XOR is own inverse, just with correct round key Designed to be as simple as possible 01/28/2009 40

AES Key Expansion n Take 128/192/256 -bit key and expand into array of 44/52/60 32 -bit words Start by copying key into first 4 words Then loop creating words that depend on values in previous and 4 places back n n n in 3 of 4 cases just XOR these together every 4 th has S-box + rotate + XOR constant of previous before XOR together Designed to resist known attacks 01/28/2009 41

AES Decryption n n AES decryption is not identical to encryption because steps are done in reverse But can define an equivalent inverse cipher with steps as for encryption n but using inverses of each step with a different key schedule Works since result is unchanged when n n swap byte substitution & shift rows swap mix columns and add (tweaked) round key 01/28/2009 42

Implementation Aspects n Can efficiently implement on 8 -bit CPU n n byte substitution works on bytes using a table of 256 entries shift rows is simple byte shifting add round key works on byte XORs mix columns requires matrix multiply in GF(28) which works on byte values, can be simplified to use a table lookup 01/28/2009 43

Implementation Aspects n Can efficiently implement on 32 -bit CPU n n n redefine steps to use 32 -bit words can precompute 4 tables of 256 -words then each column in each round can be computed using 4 table lookups + 4 XORs at a cost of 16 Kb to store tables Designers believe this very efficient implementation was a key factor in its selection as the AES cipher 01/28/2009 44

Next Class n n Confidentiality of symmetric encryption Read Chapters 7, 8, 9 01/28/2009 45
 Management directive 715
Management directive 715 The 10's complement of (715)8 is
The 10's complement of (715)8 is 715/270725 simplified
715/270725 simplified Management directive 715
Management directive 715 Privat security
Privat security Osi security architecture in hindi
Osi security architecture in hindi Guide to network security
Guide to network security Wireless security in cryptography
Wireless security in cryptography Electronic mail security in network security
Electronic mail security in network security Security guide to network security fundamentals
Security guide to network security fundamentals Security guide to network security fundamentals
Security guide to network security fundamentals Network security monitoring nsm open systems
Network security monitoring nsm open systems Network systems design using network processors
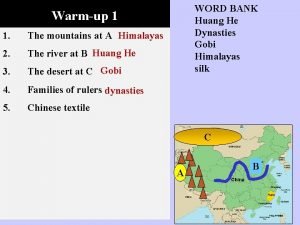
Network systems design using network processors Shang dynasty yellow river
Shang dynasty yellow river Where is the huang he river
Where is the huang he river Va cooperative studies program
Va cooperative studies program Qin shi huang quotes
Qin shi huang quotes Qin shi huang ror
Qin shi huang ror Jimmy huang nottingham
Jimmy huang nottingham Dr meng huang
Dr meng huang Linear regression andrew ng
Linear regression andrew ng Dr hanxian huang
Dr hanxian huang Huang he river valley
Huang he river valley Huang zeku
Huang zeku Protopay
Protopay Cvpr
Cvpr Peninggalan sungai huang ho
Peninggalan sungai huang ho Bonnie huang hall
Bonnie huang hall Yicheng huang
Yicheng huang Brittany huang
Brittany huang What cultural hearth was in the huang he river basin?
What cultural hearth was in the huang he river basin? Huang he pronunciation
Huang he pronunciation Minlie huang
Minlie huang Zeyi huang
Zeyi huang Norden huang
Norden huang Hubert huang
Hubert huang Junzhou huang
Junzhou huang Huang he river
Huang he river Criss-cross attention
Criss-cross attention Tiffany huang death
Tiffany huang death Huang he flodkultur
Huang he flodkultur Huang he
Huang he Cheese reporter
Cheese reporter Dijiang huang
Dijiang huang Imperador qin shi huang
Imperador qin shi huang Haomiao huang
Haomiao huang