Elgamal demonstration project on calculators TI83 Gerard Tel

Elgamal demonstration project on calculators TI-83+ Gerard Tel Utrecht University With results from Jos Roseboom and Meli Samikin Workshop Elgamal

Overview of the lecture 1. 2. 3. 4. 5. History and background Elgamal (Diffie Hellman) Discrete Log: Pollard rho Experimentation results Structure of Function Graph: Cycles, Tails, Layers 6. Conclusions Workshop Elgamal 2

1. History and background 1. 2003, lecture for school teachers about Elgamal 2. 2006, lecture with calculator demo Why Elgamal, not RSA? • Functional property easy to show • Security: rely on complexity • Compare exponentiation and DLog Workshop Elgamal 3

Math: Modular arithmetic • Compute modulo prime p (95917) with 0, 1, … p-2, p-1 • Generator g of order q (prime) • Rules of algebra are valid (ga)k = (gk)a Secure application: p has ~309 digits!! Workshop Elgamal 4

Calculator TI-83, 83+, 84+ • Grafical, 14 digit • Programmable • Generally available in VWO (preacademic school type in the Netherlands) • Cost 100 euro (free for me) Workshop Elgamal 5

The Elgamal program • Ceasar cipher (symmetric) • Elgamal parameter and key generation • Elgamal encryption and decryption • Discrete Logarithm: Pollard Infeasible problem!! But doable for 7 digit modulus Workshop Elgamal 6

2. Public Key codes The problem of Key Agreement: • A and B are on two sides of a river • They want to have common z • Oscar is in a boat on the river • Oscar must not know z Workshop Elgamal 7

Solution: Diffie-Hellman • Alice takes random a, shouts b = ga • Bob takes random k, shouts u = gk • Alice computes z = ua = (gk)a • Bob computes z = bk = (ga)k The two numbers are the same The difference in complexity for A&B and O is relevant Workshop Elgamal 8

What does Oscar hear? Oscar sees the communication, but not the secrets Seen: 1. Public 2. Public b = ga u = gk Not computable: 1. Secret a, k 2. Common z This needs discrete logarithm Workshop Elgamal 9

The Elgamal program • In class use • Program, explanation, slides on website • Program extendible • Booklet with ideas for experimenting, papers • (All in Dutch!) http: //people. cs. uu. nl/gerard/Cryptografie/Elgamal/ Workshop Elgamal 10

3. Pollard Rho Algorithm • Fixed p (modulus), g, q (order of g); G is set of powers of g • Discrete Logarithm problem: – Given y in G – Return x st gx = y • Pollard Rho: randomized, √q time Workshop Elgamal 11

Pollard Rho: Representation • Representation of z: z = ya. gb • Two representations of same number reveil log y: If ya. gb = yc. gd, then y = g(b-d)/(c-a) • Goal: find 2 representations of one number z (value does not matter) Workshop Elgamal 12

Strategy: Birthday Theorem • All values z = ya. gb are in G • Birthday Theorem: In a random sequence, we expect a collision after √q steps • Simulate effect of random sequence by pseudorandom function: zi+1 = f (zi) (Keep representation of each zi) Workshop Elgamal 13

Cycle detection • Detect collision by storing previous values: too expensive • Floyd cycle detection method: – Develop two sequences: zi and ti – Relation: ti = z 2 i – Collision: ti = zi, i. e. , zi = z 2 i In each round, z “moves” one step and t moves two steps. Workshop Elgamal 14

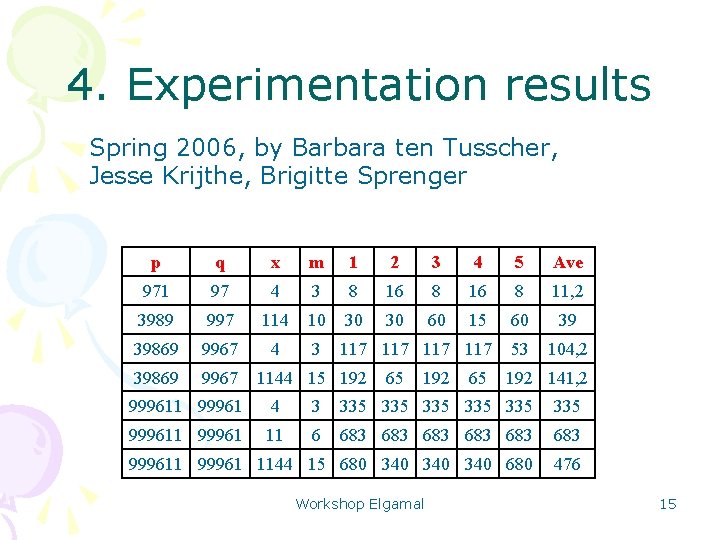
4. Experimentation results Spring 2006, by Barbara ten Tusscher, Jesse Krijthe, Brigitte Sprenger p q x m 1 2 3 4 5 Ave 971 97 4 3 8 16 8 11, 2 3989 997 114 10 30 30 60 15 60 39 39869 9967 4 3 117 117 53 104, 2 39869 9967 1144 15 192 65 192 141, 2 999611 99961 4 3 335 335 335 999611 99961 11 6 683 683 683 999611 99961 1144 15 680 340 340 680 476 Workshop Elgamal 15

Observations • Average number of iterations coincides well with √q • Almost no variation within one row • Is this a bug in the program? ? – Bad randomization in calculator? – Or general property of Pollard Rho? Workshop Elgamal 16

5. Function graph • Function f: zi -> zi+1 defines graph • Out-degree 1, cycles with in-trees • Length, component, size • Graph is the same when algorithm is repeated with the same input • Starting point differs • As zi = z 2 i, i must be multiple of cycle length Workshop Elgamal 17

Layers in a component • Layer of node measure distance to cycle in terms of its length l: – Point z in cycle has layer 0 – Point z is in layer 1 if f(l)(z) in cycle – Point z is in layer c if f(c. l)(z) in cycle • Lemma: z 0 in layer c gives c. l iter. • Is there a dominant component or layer? Workshop Elgamal 18

Layers 0 and 1 dominate Probability theory analysis by Meli Samikin Lemma: Pr(layer ≤ 1) = ½ Proof: Assume collision after k steps: z 0 -> z 1 -> … -> zk-1 -> ? ? Layer of z 0 is 0 if zk = z 0, Pr = 1/k Layer of z 0 is 1 if zk = zj < k/2, Pr ≈ 1/2 Workshop Elgamal 19

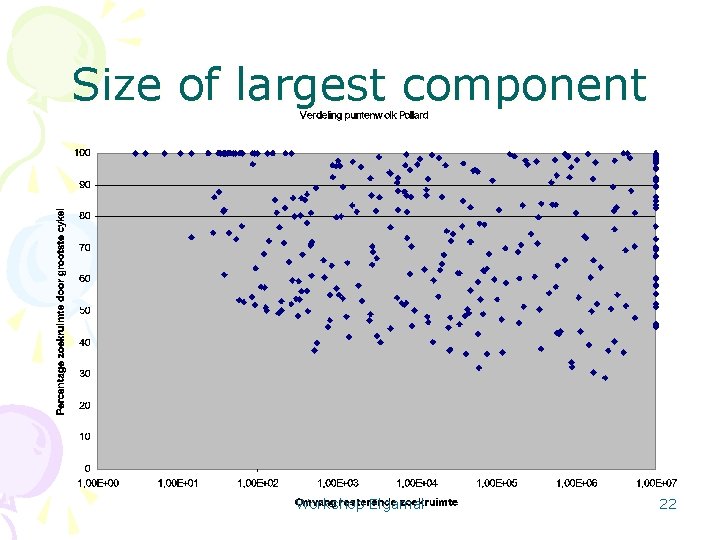
Dominant Component Lemma: Random z 0 and w 0, Pr(same component) > ½. Proof: First collision after k steps: z 0 -> z 1 -> … -> zk-1 -> ? ? w 0 -> w 1 -> … -> wk-1 -> ? ? Pr ( z meets other sequence ) = ½. Then, w-sequence may collide into z. Workshop Elgamal 20

Experiments: dominance • Jos Roseboom: count points in layers of each component • Plays national korfbal team • World Champion 2007, november, Brno. Workshop Elgamal 21

Size of largest component Workshop Elgamal 22

Conclusions • Elgamal + handcalculators = fun • Functional requirements easier to explain than for RSA • Security: experiment with DLog • Pollard, only randomizes at start • Iterations: random variable, but takes only limited values • Most often: size of heaviest cycle Workshop Elgamal 23

Rabbit Formula • Ontsleutelen is: v delen door ua • u(a 1+a 2) is: ua 1. ua 2 • Deel eerst door ua 1 en dan door ua 2 • Team 1: bereken v’ = Deca 1(u, v) Team 2: bereken x = Deca 2(u, v’) Workshop Elgamal 24

Overzicht van formules • Constanten: Priemgetal p, grondtal g • Sleutelpaar: Secret a en Public b = ga • Encryptie: (u, v) = (gk, x. bk) met b Decryptie: x = v/ua met a • Prijsvraag: b = b 1 b 2. Ontsleutelen? Workshop Elgamal 25