Scomposizione dei polinomi Prof ssa A Comis 1























- Slides: 23

Scomposizione dei polinomi Prof. ssa A. Comis 1

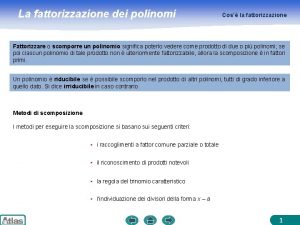
• Scomporre un polinomio significa scriverlo come prodotto di altri polinomi di grado inferiore. 2

Metodi di scomposizione • • • Raccoglimento totale a fattore comune Raccoglimento parziale a fattore comune Prodotti notevoli Trinomio particolare Abbassamento di grado mediante la regola di Ruffini. 3

Raccoglimento totale a fattore comune • Quando tutti i termini di un polinomio hanno un fattore comune, possiamo applicare la proprietà di raccoglimento. • Questo significa che mettiamo in evidenza il M. C. D. fra tutti i termini del polinomio • In questo modo eseguiamo una scomposizione del polinomio perché lo scriviamo come prodotto di due fattori. 4

Esempi • • +ax+ay+az = a(x+y+z) 3 bx 2+5 ax 2 -8 b 2 x 2 = x 2(3 b+5 a-8 b 2) 75 ax+25 ay-100 axy = 25 a(3 x+y-4 xy) 2 x(x-a)-(x-a)+3 y(x-a) = (x-a)(2 x-1+3 y) 5

Raccoglimento parziale a fattore comune • Spesso non tutti i termini del polinomio hanno un fattore comune da poter evidenziare. • Se i termini si possono raggruppare in modo da avere, in ogni gruppo, un fattore comune si può effettuare un raccoglimento parziale. • E’ importante sottolineare che i fattori ottenuti dentro le parentesi DEVONO essere uguali. 6

Esempi • +2 a+2 b+ax+bx = 2(a+b)+x(a+b) La scomposizione non è terminata perché c’è ancora una somma, però adesso è possibile effettuare un raccoglimento totale e quindi: (a+b)(2+x) 7

Altri esempi • a 2 -a-ab+b = a(a-1)-b(a-1) = (a-1)(a-b) oppure : a(a-b)-(a-b) = (a-b)(a-1) • 3 x 2 -6 ax+x-2 a = 3 x(x-2 a)+1(x-2 a) = = (x-2 a)(3 x+1) oppure : x(3 x+1)-2 a(3 x+1) = (3 x+1)(x-2 a) 8

Considerazioni • Se si vuole scomporre un polinomio, si deve innanzitutto verificare se è possibile un raccoglimento totale, cioè se TUTTI gli addendi hanno qualche fattore comune. • Se ciò non è possibile, si deve verificare la possibilità di un raccoglimento parziale per gruppi di monomi di uguale numerosità (a due, a tre e così via). 9

Altre considerazioni • La scelta dei gruppi da raccogliere non ha regole precise. E’ però fondamentale che consenta un successivo raccoglimento. • A volte un raccoglimento parziale non fa ottenere addendi con un fattore comune, pur essendo stato svolto con passaggi algebrici corretti. Se ciò accade, è opportuno rifare il raccoglimento in modo diverso. 10

Prodotti notevoli • Le regole dei prodotti notevoli possono essere lette “al contrario” ed essere applicate nella scomposizione di un polinomio. • Naturalmente è essenziale ricordarle bene per poterle riconoscere! 11

Differenza di due quadrati Ricordiamo che: a 2 -b 2 = (a-b)(a+b) e quindi, per esempio, il polinomio x 2 -4 y 2 si può considerare come (x)2 -(2 y)2 ed applicando la formula precedente si scompone così: (x-2 y)(x+2 y) 12

Esempi • • 25 x 6 -9 a 4 = (5 x 3 -3 a 2)(5 x 3+3 a 2) 4 x 2 -a 2 b 2 = (2 x-ab)(2 x+ab) 9 a 2 -16 b 2 = (3 a-4 b)(3 a+4 b) 16 a 4 -b 4 = (4 a 2 -b 2)(4 a 2+b 2) = il primo fattore rappresenta un’altra differenza di quadrati e quindi: = (2 a-b)(2 a+b)(4 a 2+b 2) 13

Quadrato di binomio Ricordiamo che: (a-b)2 = a 2 -2 ab+b 2 e (a+b)2 = a 2+2 ab+b 2 Se leggiamo “al contrario” le precedenti formule, possiamo notare che i trinomi sono formati da due quadrati e dal doppio prodotto delle loro basi. 14

Esempi • 4 x 2 -4 x+1 = (2 x)2 -2(2 x)(1)+(1)2 = (2 x-1)2 • x 2+6 x+9 = (x)2+2(x)(3)+(3)2 = (x+3)2 e quindi: • 25 a 4 b 2+20 a 2 bc 3+4 c 6 = (5 a 2 b+2 c 3)2 • 16 x 8 -24 x 4 y 3+9 y 6 =(4 x 4 -3 y 3)2 • a 6 -6 a 3 b+9 b 2 = (a 3 -3 b)2 15

Quadrato di trinomio • Ricordando che (a+b+c)2 = a 2+b 2+c 2+2 ab+2 ac+2 bc e tenendo presente i casi precedenti, risulta evidente la scomposizione dei seguenti polinomi: • x 2+y 2+4+2 xy+4 x+4 y = (x+y+2)2 • 4 x 2+9 y 2+1+12 xy-4 x-6 y = (2 x+3 y-1)2 16

Cubo di binomio • Ricordando che (a+b)3 = a 3+3 a 2 b+3 ab 2+b 3 e che (a-b)3 = a 3 -3 a 2 b+3 ab 2 -b 3 come nel quadrato di binomio, se leggiamo “al contrario” le precedenti formule, possiamo notare che i polinomi hanno 4 termini tra cui due sono cubi e gli altri due sono i tripli prodotti delle basi secondo la regola. 17

Esempi • x 3+6 x 2 y+12 xy 2+8 y 3 = = (x)3+3(x)2(2 y)+3(x)(2 y)2+(2 y)3 = = (x+2 y)3 e quindi: • a 6 -9 a 4 b+27 a 2 b 2 -27 b 3 = (a 2 -3 b)3 • 8 b 3+12 b 2+6 b+1 = (2 b+1)3 • 27 x 6 -54 x 4 y 3+36 x 2 y 6 -8 y 9 = (3 x 2 -2 y 3)3 18

Somma e differenza di cubi A questo punto risulta abbastanza semplice scomporre un polinomio applicando gli ultimi due prodotti notevoli studiati. Vediamo direttamente qualche esempio: • 8 a 3 -b 3 = (2 a-b)(4 a 2+2 ab+b 2) • a 6 -27 = (a 2 -3)(a 4+3 a 2+9) • 27 x 3+8 y 3 = (3 x+2 y)(9 x 2 -6 xy+4 y 2) 19

Trinomio particolare Se un trinomio di 2°grado è di tipo x 2+ax+b Cioè se: • Il coefficiente di grado massimo è 1; • Non consente un raccoglimento; • Non è un quadrato di binomio; Allora probabilmente è un trinomio particolare. Vediamo come riconoscerlo. 20

Come riconoscere un trinomio • Il coefficiente del termine di 1°grado può essere espresso come somma di due numeri x 0 e x 1 ; • Il termine noto è uguale al prodotto degli stessi numeri x 0 e x 1. Il trinomio particolare, quindi, si scompone cercando proprio i suddetti numeri e scrivendo (x+x 0)(x+x 1) 21

Esempi Per scomporre il trinomio a 2+5 a+6 dobbiamo cercare due numeri che abbiano per somma 5 e per prodotto 6; è facile verificare che i numeri richiesti sono 2 e 3 e quindi il suddetto trinomio si scompone in (a+2)(a+3) 22

Altri esempi • • a 2 -7 a+12 = (a-3)(a-4) x 2+6 x+8 = (x+2)(x+4) x 2 -x-12 = (x-4)(x+3) x 2+x-12 = (x+4)(x-3) Dai precedenti esempi risulta evidente che, se il termine noto è positivo i numeri sono concordi, se è negativo sono discordi. 23
 Scomposizione dei polinomi
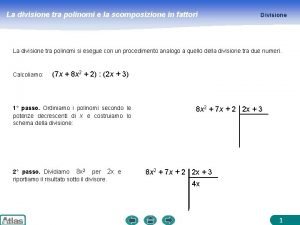
Scomposizione dei polinomi Divisione tra polinomio e binomio
Divisione tra polinomio e binomio Scomposizione polinomi in fattori primi
Scomposizione polinomi in fattori primi Ruffini metodo
Ruffini metodo Che cosa significa scomporre un polinomio
Che cosa significa scomporre un polinomio Fattorizzatore polinomi
Fattorizzatore polinomi Ruffini scomposizione online
Ruffini scomposizione online Uvm comis
Uvm comis Stable equilibrium example
Stable equilibrium example Comis latino
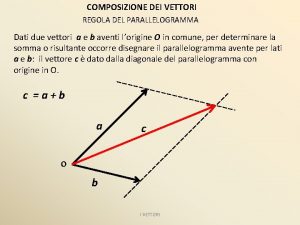
Comis latino Scomposizione dei vettori
Scomposizione dei vettori Introduzione al calcolo letterale
Introduzione al calcolo letterale Agnus dei qui tollis peccata mundi
Agnus dei qui tollis peccata mundi Francesco rinaldi la marcia dei diritti testo
Francesco rinaldi la marcia dei diritti testo Poligoni regolari immagini
Poligoni regolari immagini Scomposizione della varianza
Scomposizione della varianza P
P Raccoglimento parziale
Raccoglimento parziale Scomposizione denominatore equazioni fratte
Scomposizione denominatore equazioni fratte Tipi di caratterizzazione dei personaggi
Tipi di caratterizzazione dei personaggi Fisica: lezioni e problemi 2 soluzioni
Fisica: lezioni e problemi 2 soluzioni Scomposizione piano inclinato
Scomposizione piano inclinato 240 scomposto in fattori primi
240 scomposto in fattori primi Scomposizione della varianza
Scomposizione della varianza