ROZDZIA 5 REKURENCJA Rekurencja zwana rwnie rekursj polega

ROZDZIAŁ 5 REKURENCJA

Rekurencja zwana również rekursją, polega na wywołaniu przez funkcję samej siebie. Algorytmy rekurencyjne zastępują w pewnym sensie iteracje. Zazwyczaj zadania rozwiązywane tą techniką są wolniejsze od iteracyjnego odpowiednika, natomiast rozwiązanie niektórych problemów jest znacznie wygodniejsze.

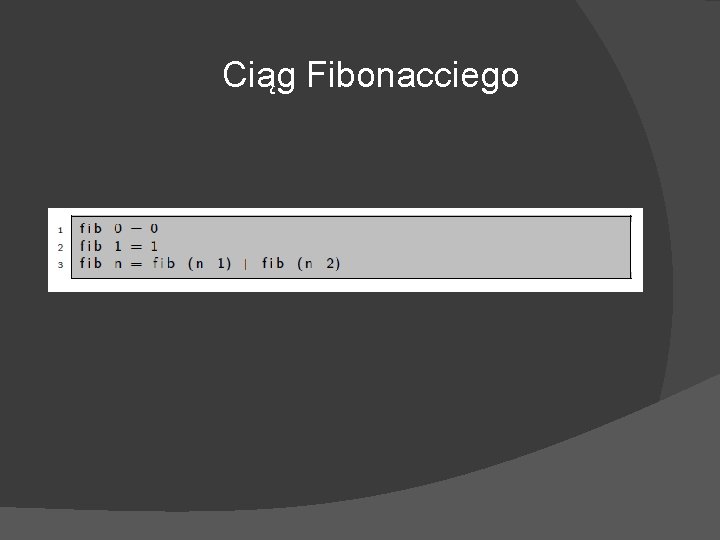
Rekurencja odgrywa podczas programowania w Haskellu bardzo dużą rolę. Nie istnieją w tym języku instrukcje takie jak pętla for czy do-while. Implementacja często powtarzających się czynności musi zatem zostać rozwiązana przez rekurencję. Dobrymi przykładami rekurencji są ciąg Fibonacciego oraz silnia.

Ciąg Fibonacciego

Silnia

Maximum Funkcja maximum zwraca największy element z zadanego zbioru, dlatego tez musi być zabezpieczona na wypadek gdyby zbiór był pusty, lub zawierał tylko jeden element. By ułatwić funkcji działanie, dzielimy ją na 3 wzorce.

1. Zbiór jest pusty zwracamy bład o podanej tresci. 2. Zbiór jest jednoelementowy funkcja zwraca jedyny element tablicy. 3. Zbiór wieloelementowy podana funkcji tablica ma wiecej niz jeden element. W tym miejscu działa rekurencja. Funkcja dzieli listę na head i tail, aż do momentu otrzymania listy jednoelementowej i porównuje head, z maximum tail (czyli wywołuje funkcje maximum dla tail).

Możemy tez uprościć sobie te funkcje poprzez zastosowanie funkcji max, pobierającej dwa argumenty i zwracającej większy z nich.

Przeanalizujmy teraz działanie rekurencji na podstawie funkcji maximum. Weźmy tablice liczb całkowitych [2, 1, 5]. q Tablice dzielimy na head(2) i tail([1, 5]) i wywołujemy funkcje maximum na tail. q. Tail jest dzielony znów na head i tail. Otrzymujemy 1 i 5 czyli dwa zbiory jednoelementowe został spełniony warunek końca rekurencji. q Porównujemy 1 i 5, funkcja zwraca 5 jako większe. q Porównujemy zwrócona wartość z head naszej tablicy. 5 jest oczywiście większe niż 2, zatem funkcja zwraca 5 jako największa wartość.

Quick. Sort w Haskellu Załóżmy, ze mamy listę elementów typu Ord do posortowania. Najefektywniej można to osiagnąć za pomocą popularnego algorytmu Quick. Sort. O ile jednak w językach imperatywnych taki algorytm zajmować może nawet kilkanaście linijek kodu, to jego implementacja w Haskellu jest dużo krótsza i bardziej przejrzysta.

Nagłówek funkcji wygląda tak: Warunek końca określa sytuacje, kiedy do posortowania zostaje pusta lista (co jest równoznaczne z tym, ze jest już posortowana):

Później przychodzi pora na główny algorytm, który działa w ten sposób: Elementy listy, które są mniejsze lub równe headowi są sortowane i umieszczane na początku listy, następnie wstawiany jest head, a po nim posortowane elementy większe lub równe headowi.

Później przychodzi pora na główny algorytm, który działa w ten sposób: Elementy listy, które są mniejsze lub równe headowi są sortowane i umieszczane na początku listy, następnie wstawiany jest head, a po nim posortowane elementy większe lub równe headowi.

Warto zaznaczyć, ze w tym algorytmie sortowanie wykonywane jest dwukrotnie (dla elementów mniejszych i większych od head). Tak wiec do użycia Quick. Sorta potrzebne będzie skorzystanie z rekurencji, która jest jednym z najważniejszych elementów programowania funkcyjnego. Do sprawdzenia, które elementy listy są większe, a które mniejsze od head zastosujemy porównanie dwóch list.

Warto zaznaczyć, ze w tym algorytmie sortowanie wykonywane jest dwukrotnie (dla elementów mniejszych i większych od head). Tak wiec do użycia Quick. Sorta potrzebne będzie skorzystanie z rekurencji, która jest jednym z najważniejszych elementów programowania funkcyjnego. Do sprawdzenia, które elementy listy są większe, a które mniejsze od head zastosujemy porównanie dwóch list.

Całość funkcji Quick. Sort w języku Haskell wygląda tak: Przykłady działania:

Myślenie rekurencyjne Chociaż wiele problemów można rozwiązać za pomocą stosowania rekurencji, istnieją także przypadki skrajne, w których użycie rekursji nie ma sensu. Na przykład: w przypadku list, takim skrajnym przypadkiem jest pusta lista, natomiast w przypadku drzewa będzie to drzewo nie posiadające żadnych dzieci.

Myślenie rekurencyjne c. d. Na podobne przypadki można sie natknąć podczas rekurencyjnego operowania na liczbach. Zazwyczaj dochodzi do tego przy stosowaniu funkcji działających na liczbach poddawanych modyfikacjom. Przykładem takiej funkcji jest silnia, która nie zadziała na rekurencyjnie na liczbach począwszy od zera, ponieważ silnie można obliczyć jedynie dla całkowitych liczb dodatnich.

Myślenie rekurencyjne c. d. Często również przypadkiem skrajnym może okazać sie identyczność. Na przykład identycznością dla mnożenia jest liczba 1, ponieważ jakakolwiek liczba pomnożona przez 1 da te sama liczbę. W przypadku sumowania list, sytuacja skrajna może być dodawanie pustej listy, której suma jest równa 0.

Myślenie rekurencyjne c. d. Często również przypadkiem skrajnym może okazać sie identyczność. Na przykład identycznością dla mnożenia jest liczba 1, ponieważ jakakolwiek liczba pomnożona przez 1 da te sama liczbę. W przypadku sumowania list, sytuacja skrajna może być dodawanie pustej listy, której suma jest równa 0.

Myślenie rekurencyjne c. d. Podsumowując: Kiedy próbujemy rozwiązać rekurencyjnie jakiś problem, dobrze jest wiedzieć jakie są przypadki, w których nie da sie dobrze zastosować rekurencji, żeby użyć ich jako przypadków skrajnych pomocnych w rozwiązaniu danego problemu.

ZADANIA Napisać funkcje rekurencyjną która obliczy długość listy 2. Napisać funkcje rekurencyjną która z listy list utworzy jedna listę ustawiając elementy jeden po drugim 3. Napisać funkcje rekurencyjną która wybierze k początkowych elementów listy 4. Napisać rekurencyjnie funkcje map 1.

Zadanie 1 dlugosc : : [a] -> Int dlugosc [] = 0 dlugosc (x: xs) = 1 + dlugosc xs dlugosc [2, 3, 4, 8] 1 +dlugosc [3, 4, 8] 1+dlugosc[8] 1+dlugosc[] 0=4

Zadanie 2 listalist : : [[a]] -> [a] listalist [] = [] listalist (x: xs) = x ++ listalist xs

Zadanie 3 take' : : Int -> [a] take' n _ | n <= 0 = [] take' _ [] = [] take' n (x: xs) = x : take' (n-1) xs

Zadanie 4 map' : : (a -> b) -> [a] -> [b] map' f [] = [] map' f (x: xs) = [f x] ++ map' f xs

Dziękujemy za uwagę Prezentację przygotowali: Marcin Górnicki Michał Szymczak Łukasz Zaleski Mateusz Magierski