Relativitselmlet Giczi Ferenc SZE Fizika s Kmia Tanszk

Relativitáselmélet Giczi Ferenc SZE, Fizika és Kémia Tanszék 2005.

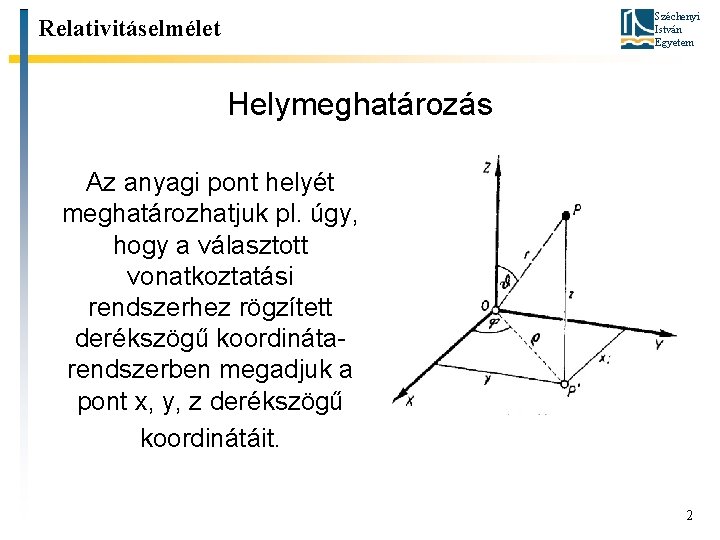
Széchenyi István Egyetem Relativitáselmélet Helymeghatározás Az anyagi pont helyét meghatározhatjuk pl. úgy, hogy a választott vonatkoztatási rendszerhez rögzített derékszögű koordinátarendszerben megadjuk a pont x, y, z derékszögű koordinátáit. 2

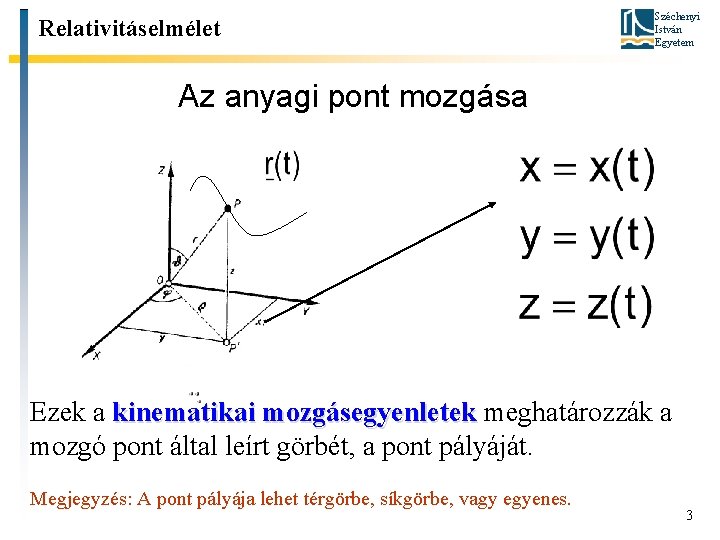
Relativitáselmélet Széchenyi István Egyetem Az anyagi pont mozgása Ezek a kinematikai mozgásegyenletek meghatározzák a mozgó pont által leírt görbét, a pont pályáját. Megjegyzés: A pont pályája lehet térgörbe, síkgörbe, vagy egyenes. 3

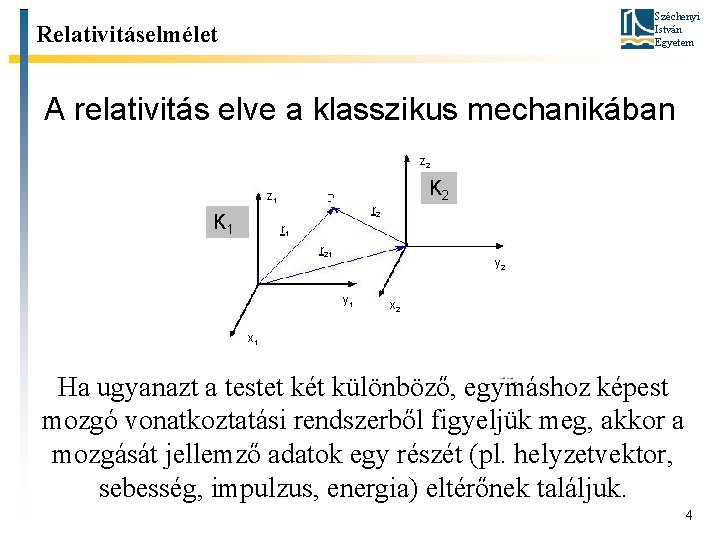
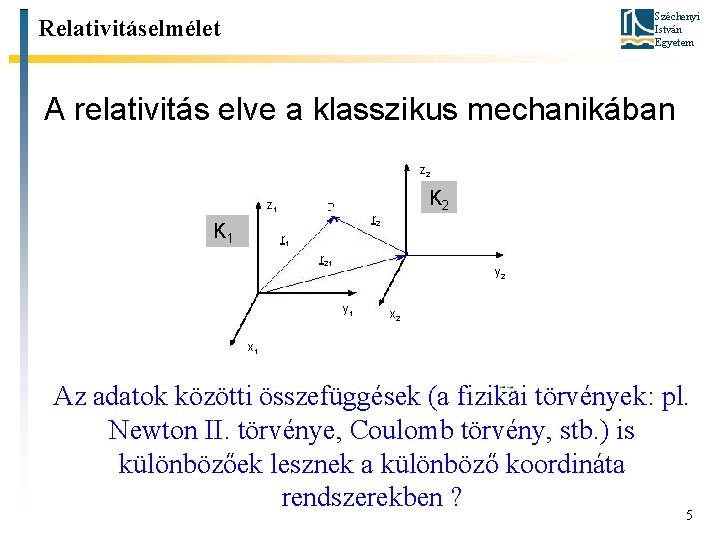
Széchenyi István Egyetem Relativitáselmélet A relativitás elve a klasszikus mechanikában z 2 z 1 K 2 r 1 r 21 y 2 y 1 x 2 x 1 Ha ugyanazt a testet két különböző, egymáshoz képest mozgó vonatkoztatási rendszerből figyeljük meg, akkor a mozgását jellemző adatok egy részét (pl. helyzetvektor, sebesség, impulzus, energia) eltérőnek találjuk. 4

Széchenyi István Egyetem Relativitáselmélet A relativitás elve a klasszikus mechanikában z 2 z 1 K 2 r 1 r 21 y 2 y 1 x 2 x 1 Az adatok közötti összefüggések (a fizikai törvények: pl. Newton II. törvénye, Coulomb törvény, stb. ) is különbözőek lesznek a különböző koordináta rendszerekben ? 5

Relativitáselmélet Széchenyi István Egyetem A klasszikus mechanika relativitás elve Különböző inerciarendszerekből nézve a mechanikai jelenségek ugyanúgy zajlanak le, és a különböző inerciarendszerekben a mechanika törvényei azonos matematikai alakban érvényesek. Következmény: Az inerciarendszerek között mechanikai kísérletekkel nem lehet különbséget tenni. (Nem lehet találni abszolút, kitüntetett inerciarendszert. ) 6

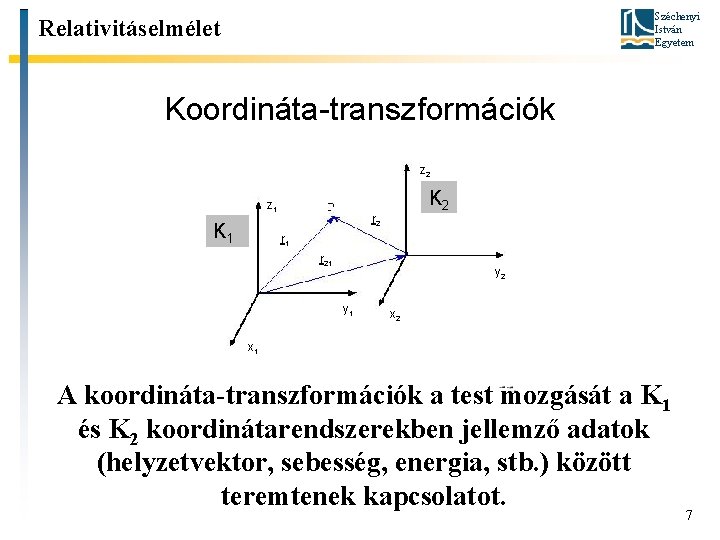
Széchenyi István Egyetem Relativitáselmélet Koordináta-transzformációk z 2 z 1 K 2 r 1 r 21 y 2 y 1 x 2 x 1 A koordináta-transzformációk a test mozgását a K 1 és K 2 koordinátarendszerekben jellemző adatok (helyzetvektor, sebesség, energia, stb. ) között teremtenek kapcsolatot. 7

Relativitáselmélet Széchenyi István Egyetem A fizikai törvények koordinátatranszformációkkal szembeni invarianciája Módszer A K 1 rendszerben felírt fizikai törvényben szereplő mennyiségeket a transzformációs összefüggések segítségével fejezzük ki a K 2 rendszer megfelelő mennyiségeivel. Így megkapjuk a kérdéses fizikai mennyiségek közötti összefüggést a K 2 rendszerben. Ha a törvény matematikai alakját tekintve azonos a két koordinátarendszerben, akkor azt mondjuk, hogy a törvény invariáns az adott transzformációra. 8

Relativitáselmélet Széchenyi István Egyetem A fizikai törvények koordinátatranszformációkkal szembeni invarianciája Ha az adott transzformációval szemben az összes fizikai törvény invariáns, akkor a transzformáció összhangban van a relativitás elvével. Ha a relativitás elvét, mint tapasztalati tényt elfogadjuk, akkor csak a vele összhangban lévő koordináta transzformációt használhatjuk. 9

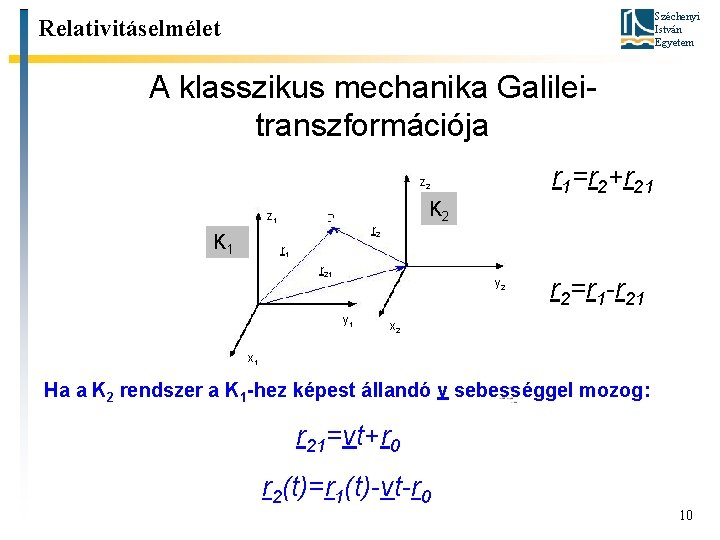
Széchenyi István Egyetem Relativitáselmélet A klasszikus mechanika Galileitranszformációja r 1=r 2+r 21 z 2 z 1 K 2 r 1 r 21 y 2 y 1 r 2=r 1 -r 21 x 2 x 1 Ha a K 2 rendszer a K 1 -hez képest állandó v sebességgel mozog: r 21=vt+r 0 r 2(t)=r 1(t)-vt-r 0 10

Széchenyi István Egyetem Relativitáselmélet A klasszikus mechanika Galileitranszformációja r 2(t)=r 1(t)-vt-r 0 x 2(t)=x 1(t)-vxt-x 0 y 2(t)=y 1(t)-vyt-y 0 z 2(t)=z 1(t)-vzt-z 0 r 2(t)=r 1(t)-vt-r 0 v 2(t)=v 1(t)-v a 2(t)=a 1(t) t 2=t 1=t Az idő a K 2 és a K 1 rendszerben azonosan telik. 11

Széchenyi István Egyetem Relativitáselmélet A klasszikus mechanika Galileitranszformációja r 2(t)=r 1(t)-vt-r 0 v 2(t)=v 1(t)-v a 2(t)=a 1(t) A klasszikus mechanika törvényei invariánsak a Galileitranszformációval szemben. 12

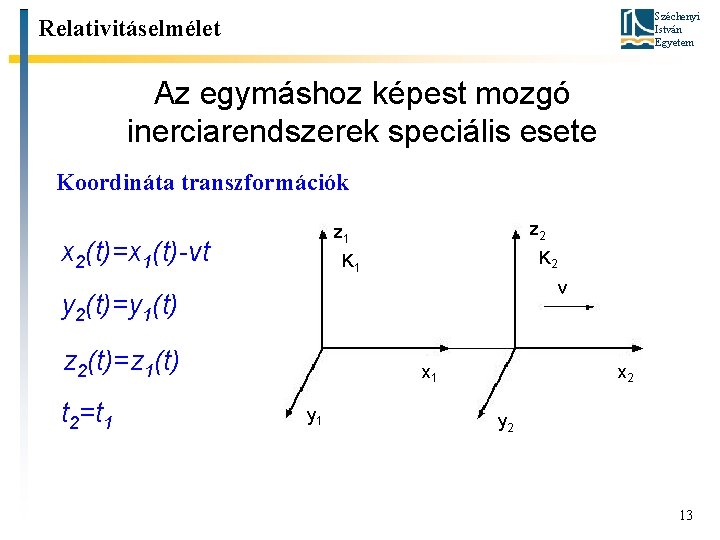
Széchenyi István Egyetem Relativitáselmélet Az egymáshoz képest mozgó inerciarendszerek speciális esete Koordináta transzformációk z 2 z 1 x 2(t)=x 1(t)-vt K 2 K 1 v y 2(t)=y 1(t) z 2(t)=z 1(t) t 2=t 1 x 1 y 1 x 2 y 2 13

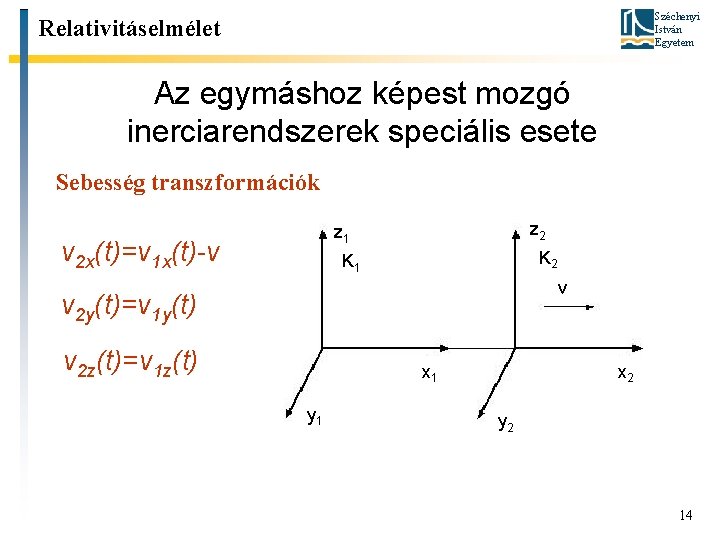
Széchenyi István Egyetem Relativitáselmélet Az egymáshoz képest mozgó inerciarendszerek speciális esete Sebesség transzformációk z 2 z 1 v 2 x(t)=v 1 x(t)-v K 2 K 1 v v 2 y(t)=v 1 y(t) v 2 z(t)=v 1 z(t) x 1 y 1 x 2 y 2 14

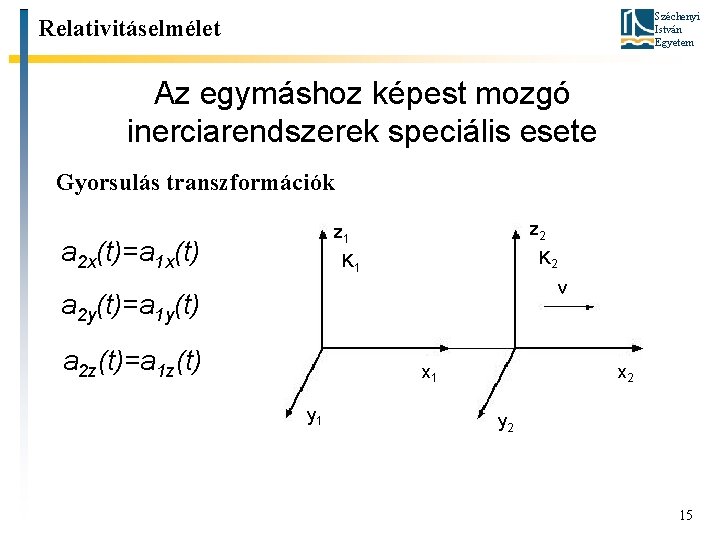
Széchenyi István Egyetem Relativitáselmélet Az egymáshoz képest mozgó inerciarendszerek speciális esete Gyorsulás transzformációk z 2 z 1 a 2 x(t)=a 1 x(t) K 2 K 1 v a 2 y(t)=a 1 y(t) a 2 z(t)=a 1 z(t) x 1 y 1 x 2 y 2 15

Széchenyi István Egyetem Relativitáselmélet A Galilei transzformáció alkalmazása Hogyan változik meg a hang terjedési sebessége, ha azt a közeghez képest állandó sebességgel mozgó koordinátarendszerben mérjük? z z 1 K 1 A közeg és a hangforrás is nyugszik K 1 -ben. v 2 x=v 1 x-v 2 v 1 x K 2 v x 1 y 1 x 2 y 2 A forrástól távolodó megfigyelő kisebb, a közeledő nagyobb hangsebességet észlel, mint a forráshoz képest nyugvó megfigyelő. 16

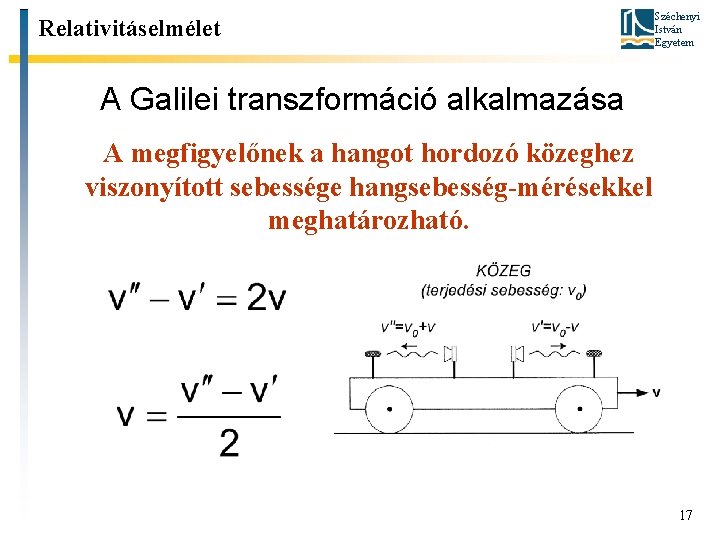
Relativitáselmélet Széchenyi István Egyetem A Galilei transzformáció alkalmazása A megfigyelőnek a hangot hordozó közeghez viszonyított sebessége hangsebesség-mérésekkel meghatározható. 17

Relativitáselmélet Széchenyi István Egyetem A relativitás elve az elektrodinamikában • A Maxwell-egyenletek a klasszikus fizikának ugyanolyan alapegyenletei, mint a Newtontörvények. • Korábban feltételezték, hogy a Maxwell-egyenletek az éterhez rögzített koordinátarendszerben érvényesek. • A fény nem más, mint egy olyan zavar, amely az éterben a rugalmas hullámokhoz hasonlóan terjed. • A vákuumban terjedő fény sebességét az éterhez viszonyított sebességnek tekintették. 18

Relativitáselmélet Széchenyi István Egyetem Próbálkozások az éter létezésének kimutatására Ötlet: Az éterhez képest mozgó Földön különböző irányokban meg kell mérni a fény terjedési sebességét. Ilyen mérésekkel meg lehetne határozni a Föld sebességét az éterhez képest. Michelson-Morley kísérlet Negatív eredmény! 19

Relativitáselmélet Széchenyi István Egyetem A fény terjedési sebessége egymáshoz képest mozgó rendszerekben A fény terjedési sebessége különböző inerciarendszerekben ugyanaz az érték, nem függ a rendszer mozgásállapotától. A fény terjedésére nem alkalmazható a Galilei-transzformáció. 20

Relativitáselmélet Széchenyi István Egyetem Az elektrodinamika és a relativitás elve A Maxwell-egyenletek nem invariánsak a Galilei-transzformációval szemben. Lorentz-transzformáció A mechanika törvényei nem invariánsak a Lorentz-transzformációval szemben. 21

Széchenyi István Egyetem Relativitáselmélet A Lorentz-transzformáció összefüggései Az idő nem azonosan telik a két rendszerben! Az időt is transzformálni kell! 22

Relativitáselmélet Széchenyi István Egyetem Egységes koordináta-transzformáció Elfogadjuk a Galilei-transzformációt, és a Maxwell-egyenleteket hibásnak minősítjük. Elfogadjuk a Lorentz-transzformációt és a mechanika törvényeit úgy kell átalakítani, hogy azok invariánsak legyenek. 23

Relativitáselmélet Széchenyi István Egyetem A speciális relativitáselmélet Einstein-féle posztulátumai • Minden fizikai folyamatra érvényes a relativitás elve. • A vákuumban terjedő fény sebessége minden inerciarendszerben azonos, univerzális állandó. • Az étert nem tekinthetjük fényhordozó közegnek. • Az étert nem tekinthetjük kitüntetett vonatkoztatási rendszernek. Elveszítette értelmét, hogy az éter létét feltételezzük. 24

Széchenyi István Egyetem Relativitáselmélet A Lorentz-transzformáció összefüggései Az Einstein-féle alapelvekből levezethetők. Kis sebességekre visszakapjuk a Galilei-transzformációt. A vákuumbeli fénysebesség határsebesség szerepét játssza. 25

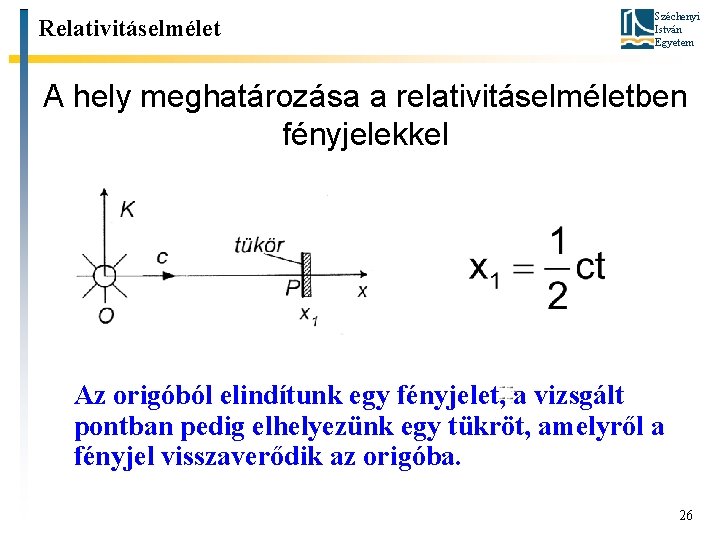
Relativitáselmélet Széchenyi István Egyetem A hely meghatározása a relativitáselméletben fényjelekkel Az origóból elindítunk egy fényjelet, a vizsgált pontban pedig elhelyezünk egy tükröt, amelyről a fényjel visszaverődik az origóba. 26

Széchenyi István Egyetem Relativitáselmélet Az órák szinkronizálása fényjelekkel t=0 időpillanatban az origóban egy fényjelet hozunk létre. Az origótól l távolságra lévő pontba a fényjel t=l/c idő alatt ér. Az órát erre az időpontra kell beállítani és akkor indítani, amikor a fényjel odaér. 27

Relativitáselmélet Széchenyi István Egyetem Az időtartamok relativitása Tegyük fel, hogy a K 2 rendszerben azonos helyen lejátszódik két esemény. I. esemény: pl. egy lámpa kigyullad II. esemény: pl. egy lámpa kialszik A két esemény között eltelt idő K 2 –ben: 28

Relativitáselmélet Széchenyi István Egyetem Az időtartamok relativitása A két esemény között eltelt idő K 2 –ben: 29

Széchenyi István Egyetem Relativitáselmélet Mozgási és nyugalmi időtartam, idődilatáció Két esemény között eltelt időtartamok is különbözőek. Mivel ezért Az események helyéhez képest mozgó megfigyelő az események között eltelt időt hosszabbnak találja, mint az eseményekhez képest nyugvó megfigyelő. 30

Relativitáselmélet Széchenyi István Egyetem Hogyan határozható meg egy rendszerhez képest mozgó tárgynak a mozgásirányba eső mérete? A tér különböző pontjaiban található szinkronizált órák közül kiválasztunk kettőt, amelyek közül az egyik a tárgy egyik végének elhaladását ugyanabban az időpillanatban jelzi, mint a másik a tárgy másik végének elhaladását. A mozgó tárgy mozgásirányba eső hossza egyenlő a két óra távolságával. 31

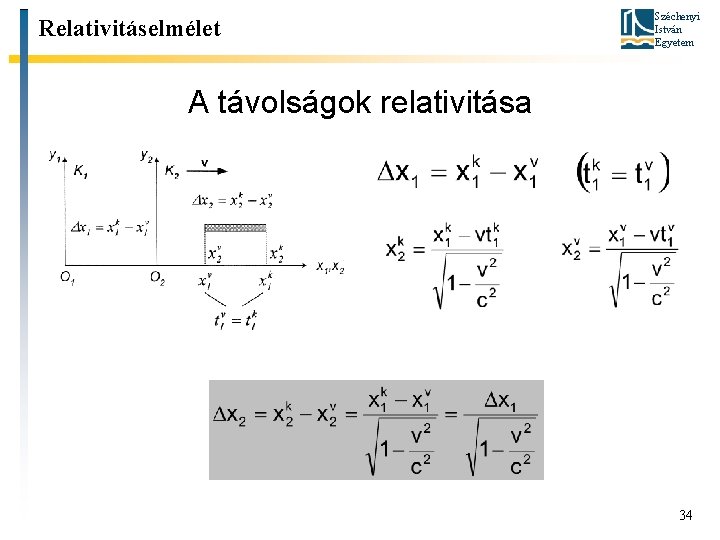
Széchenyi István Egyetem Relativitáselmélet A távolságok relativitása Számítsuk ki, hogy milyen eredményre vezet egy rúd hosszának mérése egymáshoz képest mozgó inerciarendszerekben. A rúd a K 2 -ben nyugszik. 32

Relativitáselmélet Széchenyi István Egyetem A távolságok relativitása A K 1 rendszerben a hosszt az egyidejű kezdő és végpont koordináták leolvasásával kapjuk. 33

Relativitáselmélet Széchenyi István Egyetem A távolságok relativitása 34

Relativitáselmélet Széchenyi István Egyetem A mozgási és nyugalmi hossz Lorentz-kontrakció A hosszúság is koordinátarendszertől függő mennyiség. 35

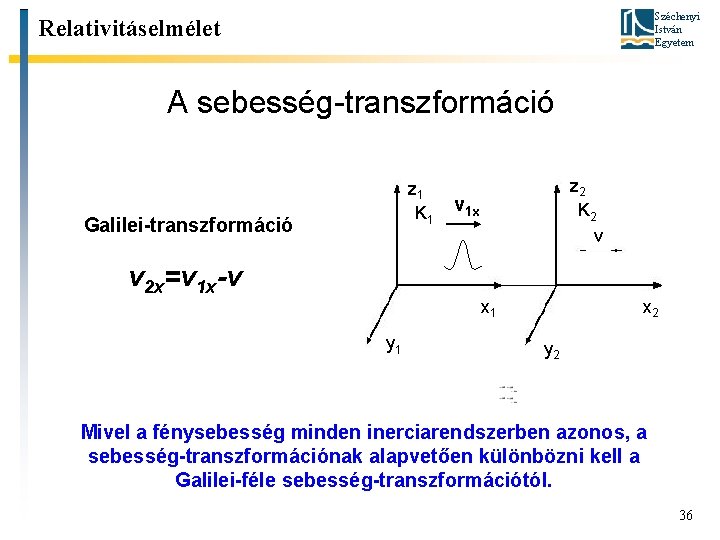
Széchenyi István Egyetem Relativitáselmélet A sebesség-transzformáció z 1 K 1 Galilei-transzformáció v 2 x=v 1 x-v z 2 K 2 v v 1 x x 1 y 1 x 2 y 2 Mivel a fénysebesség minden inerciarendszerben azonos, a sebesség-transzformációnak alapvetően különbözni kell a Galilei-féle sebesség-transzformációtól. 36

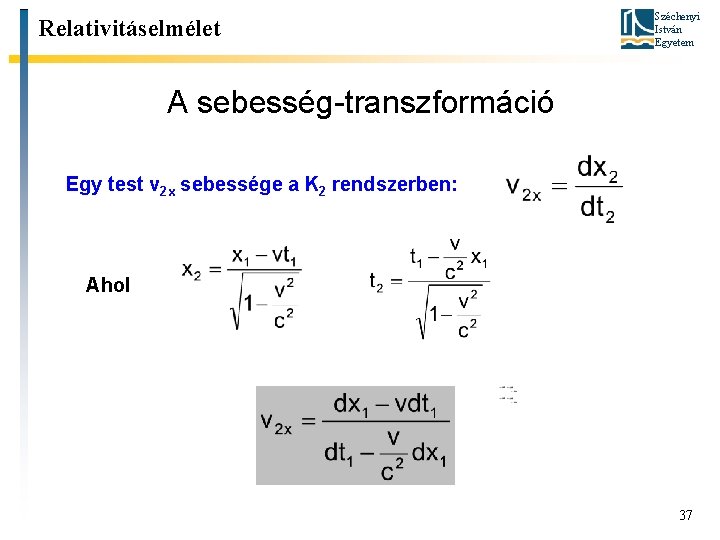
Relativitáselmélet Széchenyi István Egyetem A sebesség-transzformáció Egy test v 2 x sebessége a K 2 rendszerben: Ahol 37

Relativitáselmélet Széchenyi István Egyetem A sebesség-transzformáció A számláló és a nevező dt 1 -gyel való osztása után: Mivel Kis sebességek esetén visszaadja a Galilei-féle sebesség-transzformáció összefüggését. 38

Relativitáselmélet Széchenyi István Egyetem A négydimenziós téridő A Lorentz-transzformáció a térkoordináták mellett az időt is transzformálja. • Ezért egy esemény koordinátáinak a téridőben az (x, y, z, t) mennyiséget tekintjük. • Egy esemény a négydimenziós téridőben egy pontnak felel meg. Ha az időadatot megfelelően választjuk, az esemény koordinátáit megadó négydimenziós mennyiség egy négydimenziós vektor (NÉGYESVEKTOR) lesz. 39

Széchenyi István Egyetem Relativitáselmélet Négyesvektorok Előzmények: A háromdimenziós térben a vektor mintájául a helyzetvektor szolgál. • Vektornak nevezünk minden olyan három komponenssel megadott mennyiséget, amelynek komponensei a koordinátarendszer elforgatásakor úgy transzformálódnak, mint a helyzetvektor koordinátái. • A skaláris mennyiségek értéke nem függ a koordinátarendszer választástól. Két pont távolságának négyzete invariáns a koordinátatranszformációval szemben. 40

Relativitáselmélet Széchenyi István Egyetem Négyes állapotvektor invariáns intervallumnégyzet • A négyes állapotvektor komponensei a Lorentztranszformációval transzformálódjanak. • Két esemény közötti „négydimenziós távolság” négyzete legyen invariáns a Lorentztranszformációval szemben. Bebizonyítható, hogy az (x 1, y 1, z 1, t 1) és az (x 2, y 2, z 2, t 2) eseményekre felírt intervallumnégyzet vagy négyes-távolságnégyzet invariáns a Lorentz-transzformációval szemben. 41

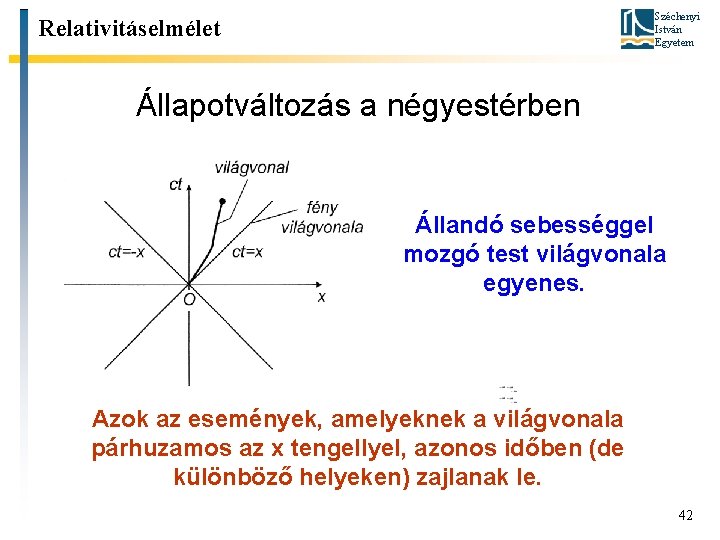
Széchenyi István Egyetem Relativitáselmélet Állapotváltozás a négyestérben Állandó sebességgel mozgó test világvonala egyenes. Azok az események, amelyeknek a világvonala párhuzamos az x tengellyel, azonos időben (de különböző helyeken) zajlanak le. 42

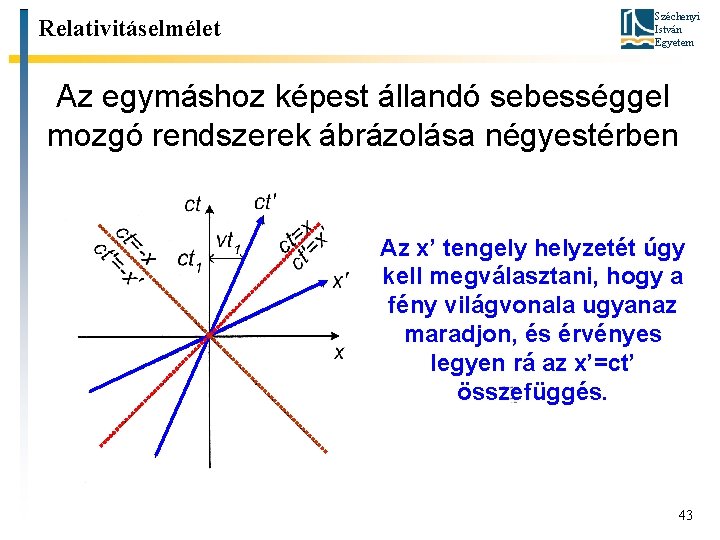
Relativitáselmélet Széchenyi István Egyetem Az egymáshoz képest állandó sebességgel mozgó rendszerek ábrázolása négyestérben Az x’ tengely helyzetét úgy kell megválasztani, hogy a fény világvonala ugyanaz maradjon, és érvényes legyen rá az x’=ct’ összefüggés. 43

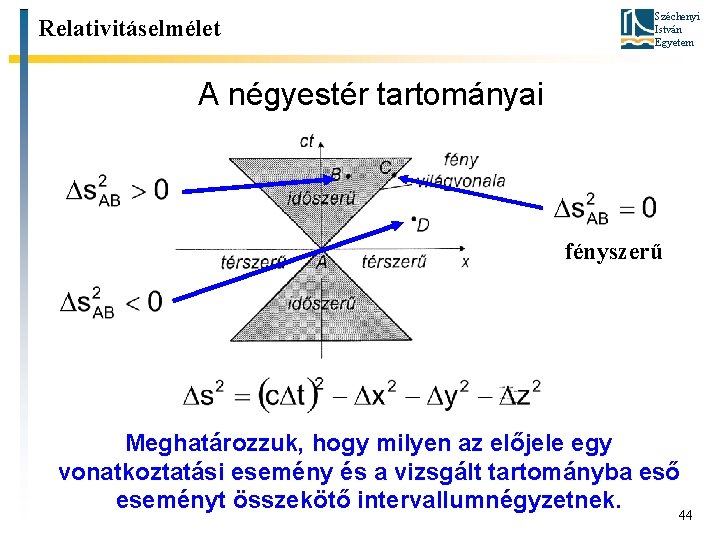
Relativitáselmélet Széchenyi István Egyetem A négyestér tartományai fényszerű Meghatározzuk, hogy milyen az előjele egy vonatkoztatási esemény és a vizsgált tartományba eső eseményt összekötő intervallumnégyzetnek. 44

Relativitáselmélet Széchenyi István Egyetem A négyestér tartományai Még sohasem figyeltek meg olyan részecskét, ami a fény vákuumbeli sebességénél gyorsabban mozgott volna. A részecskéknek időszerű világvonalat kell követnie. Az események -val jelölt időbeli szeparációját sajátidőnek vagy lokális időnel nevezik. 45

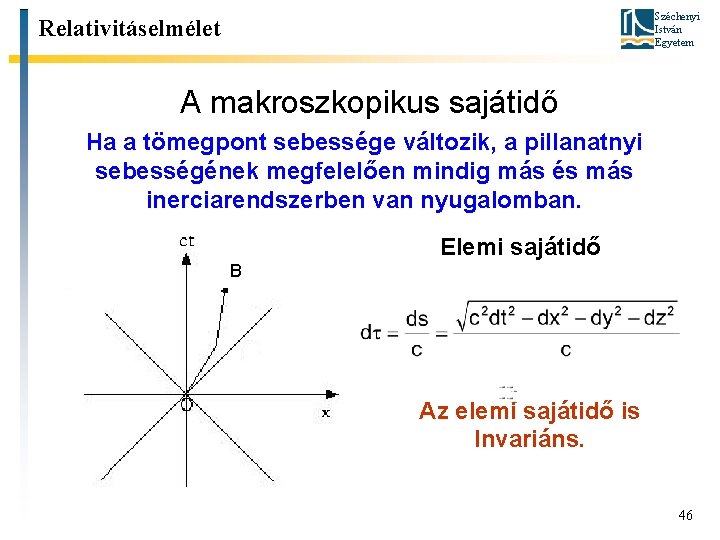
Széchenyi István Egyetem Relativitáselmélet A makroszkopikus sajátidő Ha a tömegpont sebessége változik, a pillanatnyi sebességének megfelelően mindig más és más inerciarendszerben van nyugalomban. Elemi sajátidő B Az elemi sajátidő is Invariáns. 46

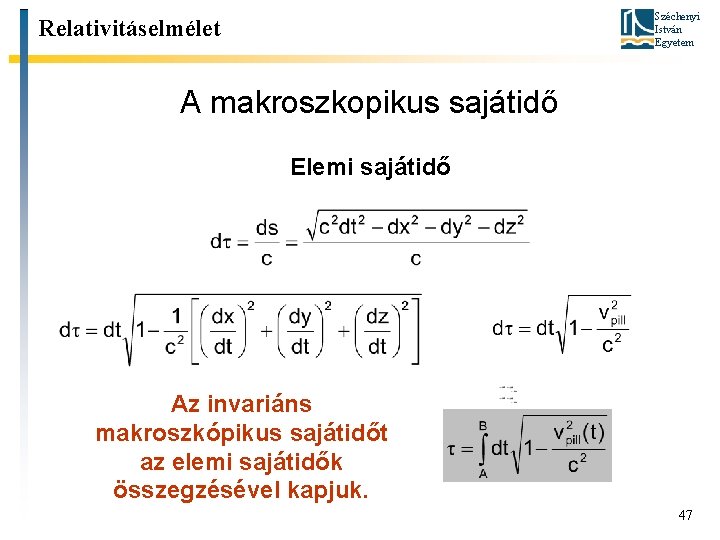
Széchenyi István Egyetem Relativitáselmélet A makroszkopikus sajátidő Elemi sajátidő Az invariáns makroszkópikus sajátidőt az elemi sajátidők összegzésével kapjuk. 47

Széchenyi István Egyetem Relativitáselmélet A relativisztikus dinamika alapjai Jellemezzük az m 0 nyugalmi tömegű tömegpont mozgását egy új négyesvektorral: egy invariáns skalár 48

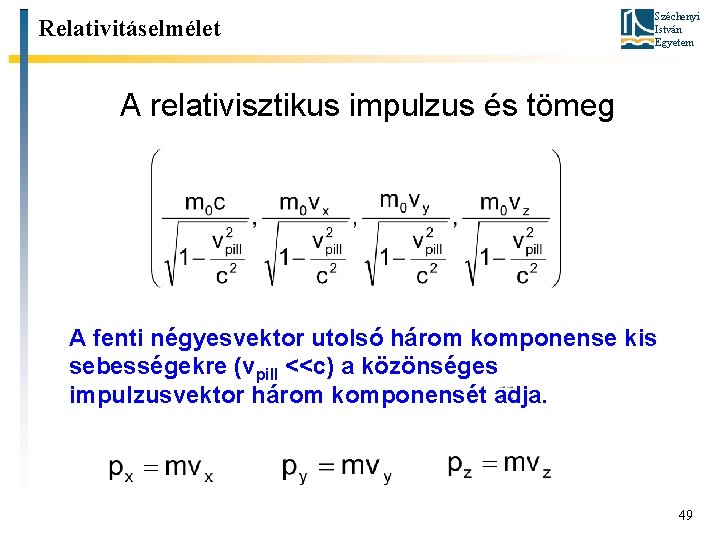
Relativitáselmélet Széchenyi István Egyetem A relativisztikus impulzus és tömeg A fenti négyesvektor utolsó három komponense kis sebességekre (vpill <<c) a közönséges impulzusvektor három komponensét adja. 49

Széchenyi István Egyetem Relativitáselmélet A relativisztikus impulzus és tömeg A fenti négyesvektor utolsó három komponense kis sebességekre (vpill <<c) a közönséges impulzusvektor három komponensét adja. Ennek alapján: Relativisztikus tömegnövekedés (több direkt kísérlet igazolta) 50

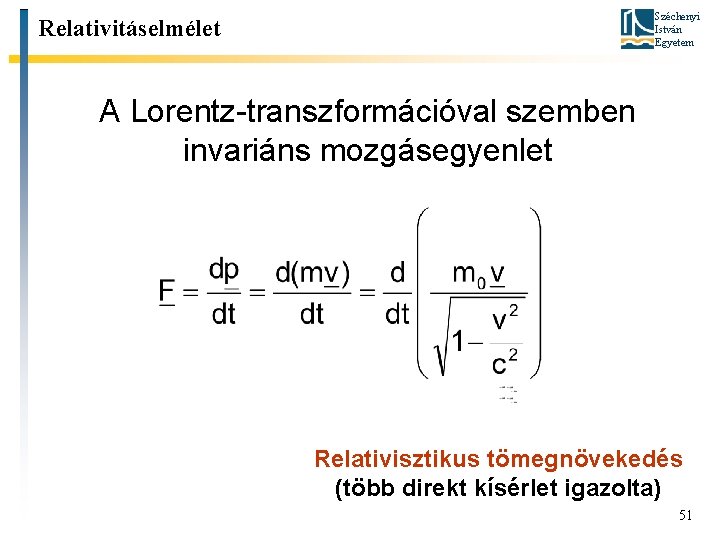
Széchenyi István Egyetem Relativitáselmélet A Lorentz-transzformációval szemben invariáns mozgásegyenlet Relativisztikus tömegnövekedés (több direkt kísérlet igazolta) 51

Széchenyi István Egyetem Relativitáselmélet Az energia a relativitáselméletben A munkatétel értelmében: Ha a tömegpontnak nincs helyzeti energiája Teljes energia változás 52

Relativitáselmélet Széchenyi István Egyetem Az energia a relativitáselméletben 53

Relativitáselmélet Széchenyi István Egyetem Az energia a relativitáselméletben Ez azt jelenti, hogy ha nincs helyzeti energia, akkor a munkatétel alapján az energiának az alábbi kifejezés felel meg: 54

Relativitáselmélet Széchenyi István Egyetem Az energia a relativitáselméletben Egy rendszerben az energia és a tömeg változása mindig együtt jár, egymással arányosan történik. 55

Relativitáselmélet Széchenyi István Egyetem Az energia a relativitáselméletben E(v) megváltozása a klasszikus mozgási energia megváltozásával egyenlő. 56

Széchenyi István Egyetem Relativitáselmélet A nyugalmi energia és a tömeghiány A relativitáselméletben a klasszikus mozgási energiának megfelelő kifejezés: Nyugalmi energia A tapasztalatok alapján a nyugalmi energia részben vagy egészben át tud alakulni másfajta energiává. 57