Redox in Magmatic Systems Activities in NonIdeal Solutions

















- Slides: 24

Redox in Magmatic Systems Activities in Non-Ideal Solutions Lecture 10

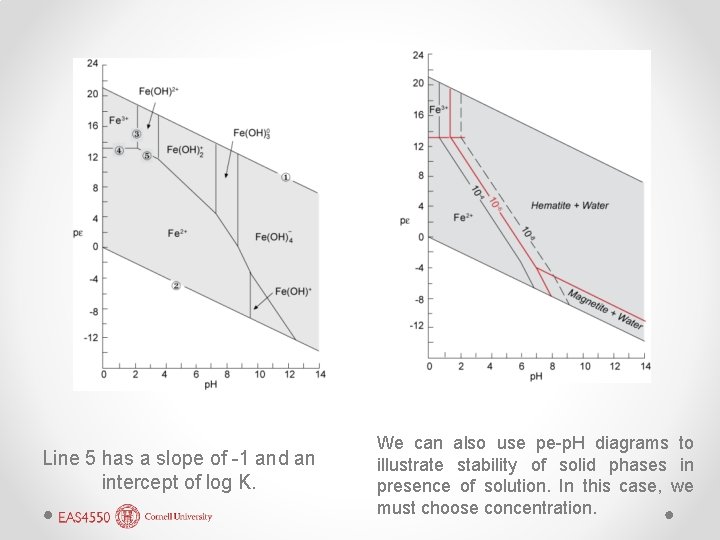
Line 5 has a slope of -1 and an intercept of log K. We can also use pe-p. H diagrams to illustrate stability of solid phases in presence of solution. In this case, we must choose concentration.

More about pe-p. H diagrams • pe-p. H diagrams are a kind of stability or predominance diagram. • They differ from phase diagrams because lines indicate not phase boundaries, but equal concentrations. o There is only 1 phase in this diagram – an aqueous solution. • Regions are regions of predominance. o The aqueous species continue to exist beyond their fields, but their concentrations drop off exponentially.

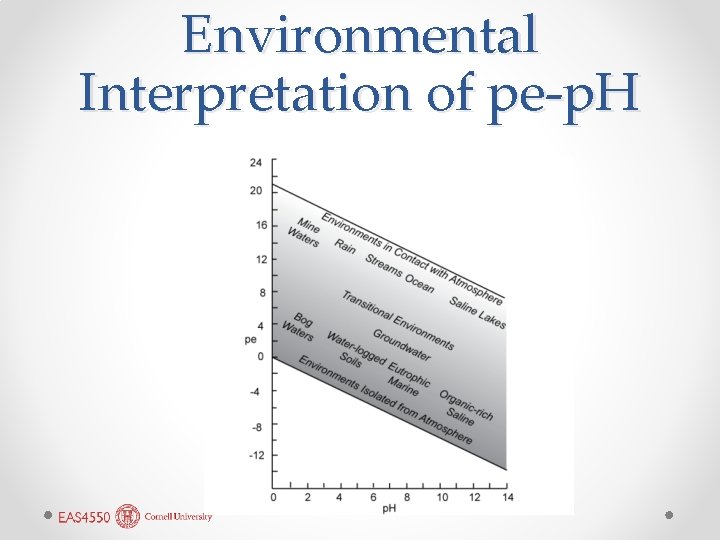
Environmental Interpretation of pe-p. H

Redox in Magmas

Oxygen Fugacity • Igneous geochemists use oxygen fugacity ƒO 2 to represent the redox state of the system. Hence, the oxidation of ferrous to ferric iron would be written as: 2 Fe. O + O 2(g) = Fe 2 O 3 • For example, oxidation of magnetite to hematite: 2 Fe 3 O 4+ ½O 2(g) = 3 Fe 2 O 3 • (Actually, there isn’t much O 2 gas in magmas. Reaction more likely mediated by water and hydrogen).

Redox in Magmatic Systems • For magnetite-hematite • 2 Fe 3 O 4+ ½O 2(g) = 3 Fe 2 O 3 • assuming the two are pure solids • At a temperature such as 1000 K

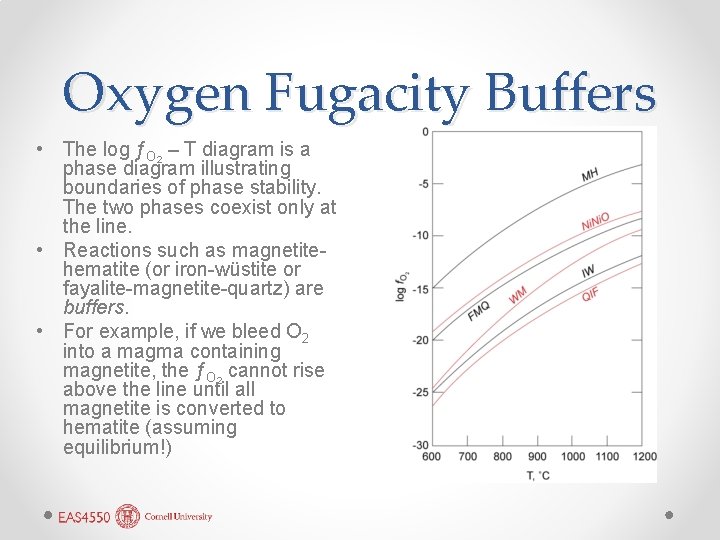
Oxygen Fugacity Buffers • The log ƒO 2 – T diagram is a phase diagram illustrating boundaries of phase stability. The two phases coexist only at the line. • Reactions such as magnetitehematite (or iron-wüstite or fayalite-magnetite-quartz) are buffers. • For example, if we bleed O 2 into a magma containing magnetite, the ƒO 2 cannot rise above the line until all magnetite is converted to hematite (assuming equilibrium!)

Real Solutions: Minerals and Magmas Chapter 4

We will cover Chapter 4 only through section 4. 6 (page 144). You will not be responsible for the remaining material in the chapter.

Power of Solutions • Our thermodynamics would be so much simpler if all solutions behaved ideally! Even simpler if there were no solutions at all! • But, once we learn how to handle them, we’ll see that we can use solution behavior to do some real geochemistry and learn things about the Earth. o Because the distribution of Mg and Fe between olivine and a magma depends on temperature, we can use the observed distribution to determine magma temperatures. o We can predict the temperature at which K- and Na-feldspar will exsolve and use this to determine metamorphic temperatures. o We can actually predict the plagioclase-spinel peridotite phase transition o We can determine equilibration temperatures of garnet peridotites.

In This Chapter • We’ll learn how to handle non-ideal solutions • Learn how to construct phase diagrams from thermodynamic data • Learn how thermodynamics is used for geothermometry and geobarometry • See how thermodynamics can be used to predict the sequence of minerals precipitating from magma.

Non-Ideality • We found a useful approach to non-ideality in electrolyte solutions (Debye-Hückel), but there are many other kinds of non-ideal solutions, including solids, liquid silicates, etc. • Some substances undergo spontaneous exsolution (oil and water; K- and Na-feldspar; clino- and orthopyroxene; silicate and sulfide magmas). When that happens, we know the solution is quite non-ideal (ideal solutions should always be more stable than corresponding physical mixtures).

Margules Equations • When you need to fit an empirical function to an observation and don’t fully understand the underlying phenomena, a power series is a good approach because it of its versatility. • So, for example, we can express the excess volume of a solution (e. g. , alcohol and water) as: • where X 2 is the mole fraction of component 2 and A, B, C, … are constants, Margules parameters, to be determined empirically (e. g. , by curve fitting).

Symmetric Solutions • Let’s first look at some simple cases. One such case would be where we need only the first and second order terms. • The excess volume (and other excesses) should be entirely functions of mole fraction, so for a binary solution where X 1 = 1 - X 2, A= 0 and our equation should reduce to: • The simplest such case would be symmetric about the midpoint X 1 = X 2. • In that case, • Substituting X 1 = 1 – X 2, we find that B = -C

Interaction Parameters or • Let WV = B • W is known as an interaction parameter (volume interaction parameter in this case) because non-ideal behavior results from interactions between dissimilar species. • The interaction parameter is a function of T, P, and the nature of the solution, but not of X. • We can define similar interaction parameters for free energy, enthalpy, and entropy.

Regular Solutions • Since ∆G = ∆H-T∆S • The free energy interaction parameter is: WG = WH – TWS • Regular solutions are the special case where WS = 0 and therefore WG = WH and WG is independent of T. o what does this imply about ∆Sexcess?

Interaction Parameters and Activity Coefficients • For a binary symmetric solution, λ 1 must equal λ 2 at X 1 = X 2. • From this we can derive: • For X 2 ≈ 1 (very dilute solution of X 1), then • and WG = RT ln h • What happens when X 1 ≈ 1?

Asymmetric Solutions • More complex situation where expansion carried out to third order. • Excess free energy given by: • Activity coefficient: Calculated Free Energy at 600˚C in the Orthoclase-Albite System as a function of Albite mole fraction.

Albite-Orthoclase Free Energy at various T A 3 -D version

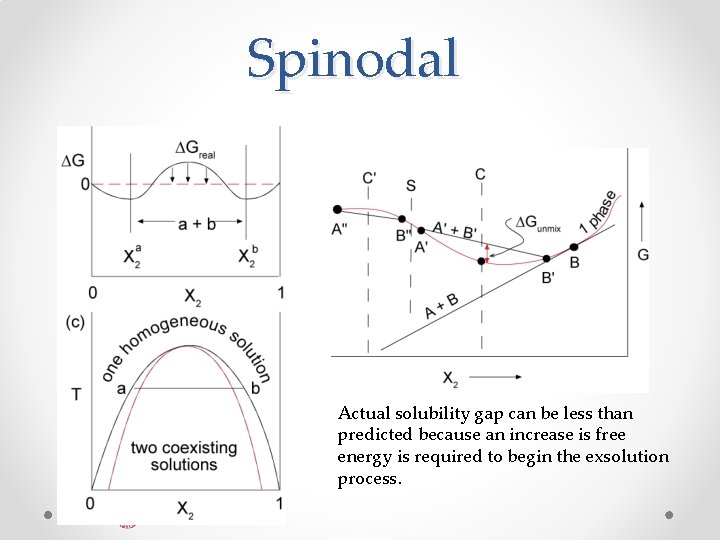
G-bar–X and Exsolution • We can use G-bar–X diagrams to predict when exsolution will occur. • Our rule is the stable configuration is the one with the lowest free energy. • A solution is stable so long as its free energy is lower than that of a physical mixture. • Gets tricky because the phases in the mixture can be solutions themselves.

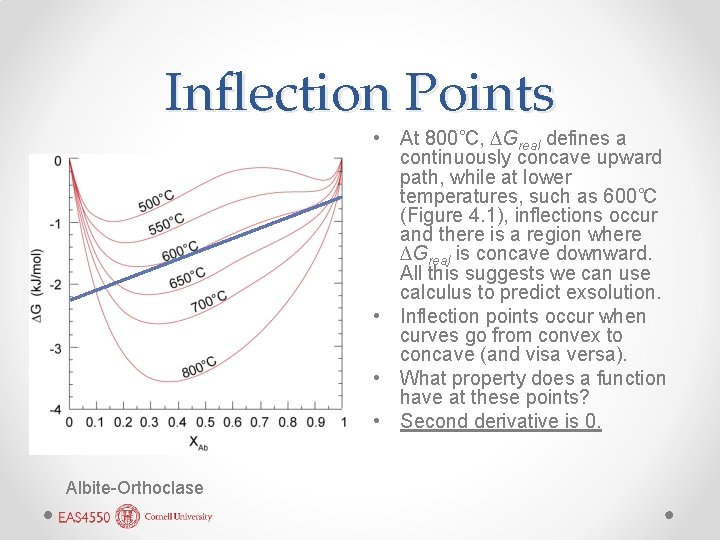
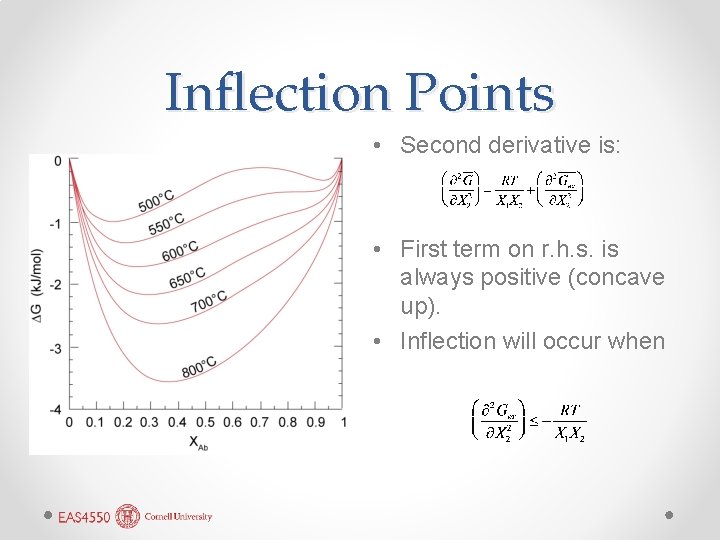
Inflection Points • At 800˚C, ∆Greal defines a continuously concave upward path, while at lower temperatures, such as 600˚C (Figure 4. 1), inflections occur and there is a region where ∆Greal is concave downward. All this suggests we can use calculus to predict exsolution. • Inflection points occur when curves go from convex to concave (and visa versa). • What property does a function have at these points? • Second derivative is 0. Albite-Orthoclase

Inflection Points • Second derivative is: • First term on r. h. s. is always positive (concave up). • Inflection will occur when

Spinodal Actual solubility gap can be less than predicted because an increase is free energy is required to begin the exsolution process.
 Magmatic intrusion
Magmatic intrusion Poise
Poise Operating activities vs investing activities
Operating activities vs investing activities Indoor and outdoor sports activities
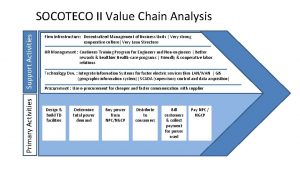
Indoor and outdoor sports activities Support activities and primary activities
Support activities and primary activities Examples of primary activities
Examples of primary activities Chapter 4 analyzing investing activities solutions
Chapter 4 analyzing investing activities solutions Accounting for merchandising operations answer key
Accounting for merchandising operations answer key Signals and systems oppenheim solutions chapter 5
Signals and systems oppenheim solutions chapter 5 Lockheed martin information systems & global solutions
Lockheed martin information systems & global solutions Decision support systems and intelligent systems
Decision support systems and intelligent systems Principles of complex systems for systems engineering
Principles of complex systems for systems engineering Embedded systems vs cyber physical systems
Embedded systems vs cyber physical systems Elegant systems
Elegant systems Cellular respiration redox
Cellular respiration redox Types of redox reactions
Types of redox reactions Which equation represents an oxidation-reduction reaction
Which equation represents an oxidation-reduction reaction Explain redox reaction
Explain redox reaction Kmn=4
Kmn=4 Redox titration
Redox titration Redox titration curve
Redox titration curve Leo goes ger
Leo goes ger Leo ger example
Leo ger example Couple redox definition
Couple redox definition Oxidation state
Oxidation state