Signal Linear system Chapter 5 DT System Analysis

Signal & Linear system Chapter 5 DT System Analysis : Z Transform Basil Hamed

Introduction Z-Transform does for DT systems what the Laplace Transform does for CT systems Z-T is used to Solve difference equations with initial conditions Solve zero-state systems using the transfer function In this chapter we will: -Define the ZT -See its properties -Use the ZT and its properties to analyze D-T systems Basil Hamed 2

Introduction In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequencydomain representation. It can be considered as a discrete-time equivalent of the Laplace transform. • The basic idea now known as the Z-transform was known to Laplace, and it was re-introduced in 1947 by W. Hurewicz. • It was later dubbed "the z-transform" by Ragazzini and Zadeh in the sampled-data control group at Columbia University in 1952 Basil Hamed 3

Introduction What is the use of Z transform? The z-transform is useful for the manipulation of discrete data sequences and has acquired a new significance in the formulation and analysis of discrete-time systems. It is used extensively today in the areas of applied mathematics, digital signal processing, control theory, population science, economics. Basil Hamed 4

5. 1 The Z-transform Basil Hamed 5

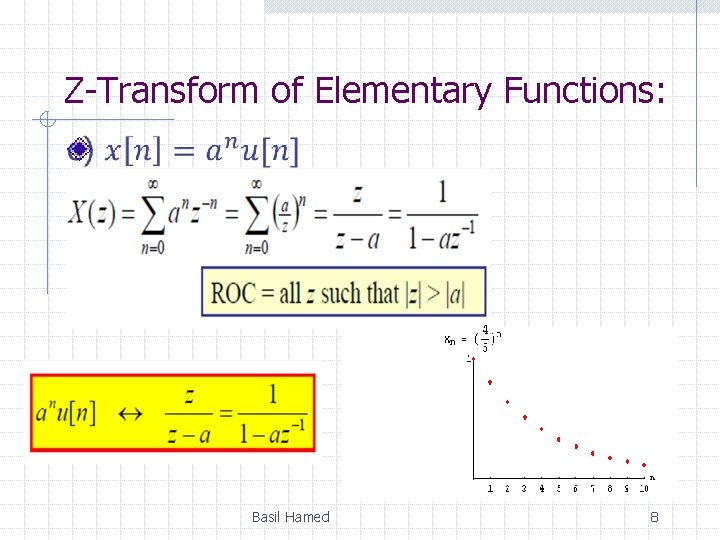
Z-Transform of Elementary Functions: Basil Hamed 6

Z-Transform of Elementary Functions: Basil Hamed 7

Z-Transform of Elementary Functions: Basil Hamed 8

Z-Transform of Elementary Functions: Basil Hamed 9

Z-Transform of Elementary Functions: Basil Hamed 10

Region of Convergence Basil Hamed 11

Region of Convergence Basil Hamed 12

Z-Transform of Elementary Functions: Basil Hamed 13

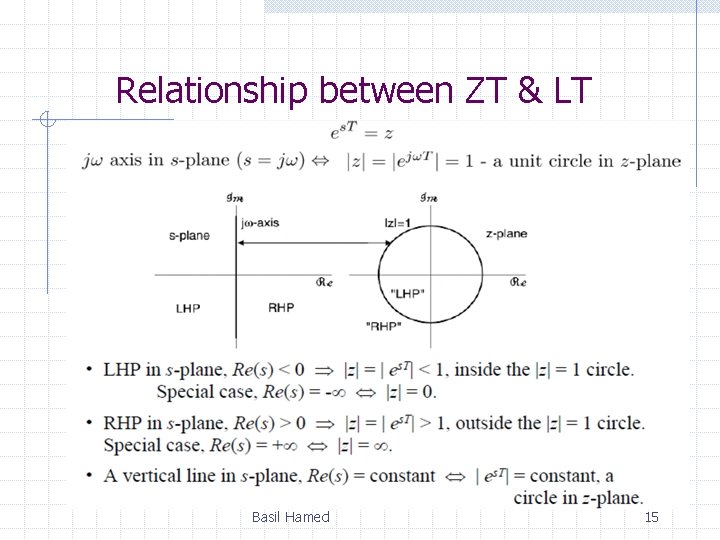
Relationship between ZT & LT Basil Hamed 14

Relationship between ZT & LT Basil Hamed 15

Relationship between ZT & LT Basil Hamed 16

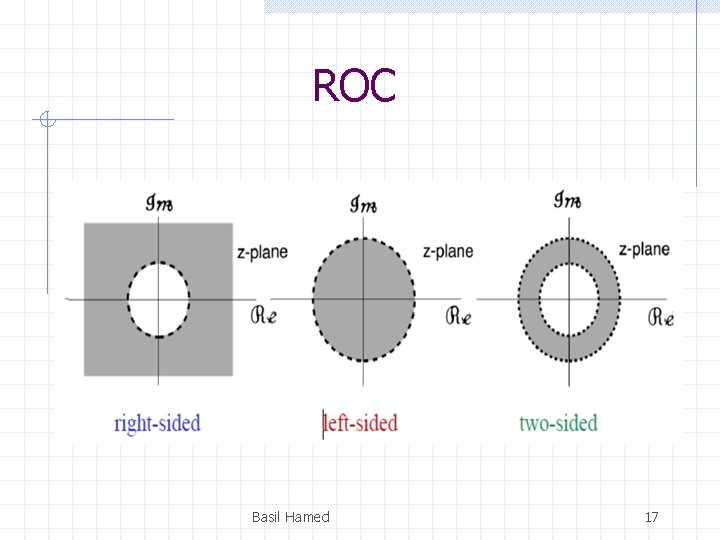
ROC Basil Hamed 17

ROC Basil Hamed 18

Table of z-transforms Basil Hamed 19

5. 2 Some Properties of The Z-Transform Example Find z-transform of Solution: Basil Hamed 20

5. 2 Some Properties of The Z-Transform Basil Hamed 21

5. 2 Some Properties of The Z-Transform Basil Hamed 22

5. 2 Some Properties of The Z-Transform Basil Hamed 23

5. 2 Some Properties of The Z-Transform Basil Hamed 24

5. 2 Some Properties of The Z-Transform Example Find z-transform of Solution: Using shift theorem, Using z-transform table Basil Hamed 25

5. 2 Some Properties of The Z-Transform Basil Hamed 26

5. 2 Some Properties of The Z-Transform Differentiation with Respect to Z Basil Hamed 27

5. 2 Some Properties of The Z-Transform Initial Value Theorem Basil Hamed 28

5. 2 Some Properties of The Z-Transform Final value Theorem Basil Hamed 29

5. 2 Some Properties of The Z-Transform Basil Hamed 30

Stability of DT Systems For the stability of the system function If the discrete rational system is stable then System is stable Basil Hamed 31

Stability of DT Systems Basil Hamed 32

Stability of DT Systems Example Basil Hamed 33

5. 2 Some Properties of The Z-Transform Convolution Basil Hamed 34

5. 2 Some Properties of The Z-Transform Basil Hamed 35

5. 2 Some Properties of The Z-Transform Basil Hamed 36

5. 2 Some Properties of The Z-Transform Example Suppose that We wish to find [yn] by finding first Y(Z) Solution Y(z)=X(z)H(z) Basil Hamed 37

The Inverse of Z-Transform There are many methods for finding the inverse of Ztransform; Three methods will be discussed in this class. 1. Direct Division Method (Power Series Method) 2. Inversion by Partial fraction Expansion 3. Inversion Integral Method Basil Hamed 38

The Inverse of Z-Transform Basil Hamed 39

The Inverse of Z-Transform Basil Hamed 40

The Inverse of Z-Transform Basil Hamed 41

The Inverse of Z-Transform Basil Hamed 42

The Inverse of Z-Transform Basil Hamed 43

The Inverse of Z-Transform Basil Hamed 44

The Inverse of Z-Transform Basil Hamed 45

The Inverse of Z-Transform Basil Hamed 46

The Inverse of Z-Transform Basil Hamed 47

The Inverse of Z-Transform Basil Hamed 48

The Inverse of Z-Transform Basil Hamed 49

The Inverse of Z-Transform Basil Hamed 50

The Inverse of Z-Transform Basil Hamed 51

The Inverse of Z-Transform Basil Hamed 52

The Inverse of Z-Transform Basil Hamed 53

The Inverse of Z-Transform Basil Hamed 54

The Inverse of Z-Transform Basil Hamed 55

The Inverse of Z-Transform Basil Hamed 56

The Inverse of Z-Transform Basil Hamed 57

The Inverse of Z-Transform Basil Hamed 58

The Inverse of Z-Transform Basil Hamed 59

Example Obtain the inverse z transform of Solution: Basil Hamed 60

Example Basil Hamed 61

Example Basil Hamed 62

Example Basil Hamed 63

Example Basil Hamed 64

The Inverse of Z-Transform Example Find Z− 1 [X(z)], where Basil Hamed 65

The Inverse of Z-Transform Basil Hamed 66

The Inverse of Z-Transform Steps Basil Hamed 67

Basil Hamed 68

Transfer Function Basil Hamed 69

Transfer Function Basil Hamed 70

Transfer Function Zero Input Response Zero State Response Basil Hamed 71

ZT For Difference Eqs. Given a difference equation that models a D-T system we may want to solve it: -with IC’s of zero Note…the ideas here are very much like what we did with the Laplace Transform for CT systems. We’ll consider the ZT/Difference Eq. approach first… Basil Hamed 72

Solving a First-order Difference Equation using the ZT Basil Hamed 73

Solving a First-order Difference Equation using the ZT Basil Hamed 74

First Order System w/ Step Input Basil Hamed 75

Solving a Second-order Difference Equation using the ZT Basil Hamed 76

Solving a Nth-order Difference Equation using the ZT Basil Hamed 77

Example System described by a difference equation y [n] – 5 y [n-1] + 6 y [n-2] = 3 f [n-1] + 5 f [n-2] Y [-1] = 11/6, y [-2] = 37/36 f [n] = 2 -n u [n] find y[n] 16 - 78

Example Basil Hamed 79

Example Find the unit impulse response of the system described by the following equation : Solution: Basil Hamed 80

Example Basil Hamed 81

Discrete-Time System Relationships Basil Hamed 82

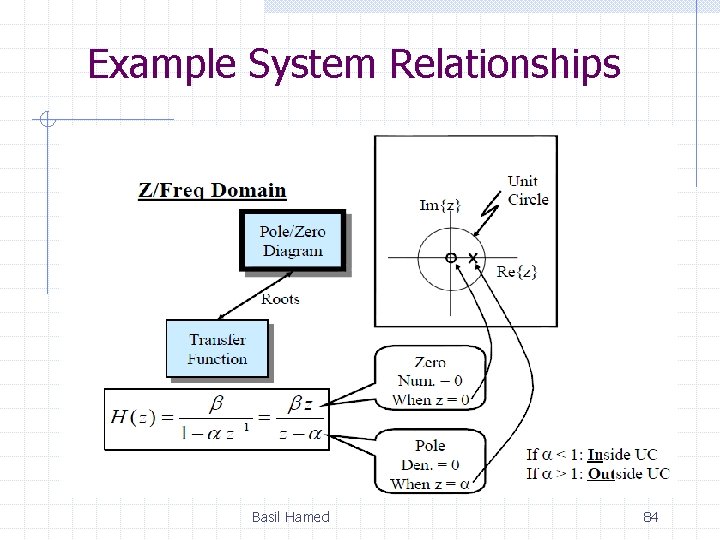
Example System Relationships Basil Hamed 83

Example System Relationships Basil Hamed 84

Example A system with impulse response produces an output Determine the corresponding input x(n). Basil Hamed 85

Solution Basil Hamed 86

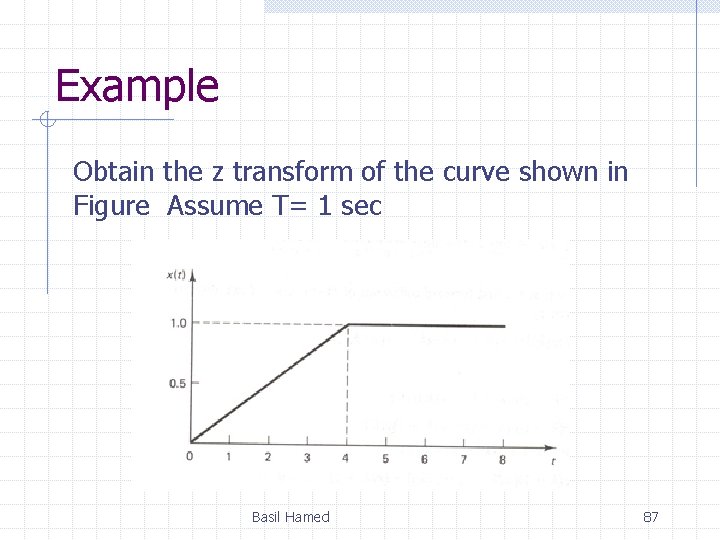
Example Obtain the z transform of the curve shown in Figure Assume T= 1 sec Basil Hamed 87

Solution Basil Hamed 88

Example Solve with y[-1]=1, y[-2]=0, and x[n]=u[n]. Basil Hamed 89

Example Basil Hamed 90