Quantum Physics of LightMatter Interactions So Se 20

Quantum Physics of Light-Matter Interactions So. Se 20 --- April 24 th to July 24 th 2020 -- Lecturer: Claudiu Genes Max Planck Institute for the Science of Light (Erlangen, Germany) -- Lecture 5 --- 29. 05. 2020 -- Genes Research Group Cooperative Quantum Phenomena

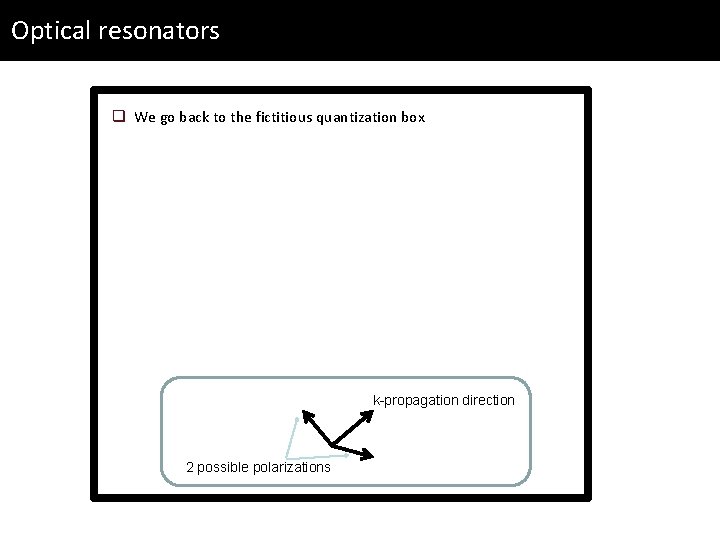
Optical resonators q We go back to the fictitious quantization box k-propagation direction 2 possible polarizations

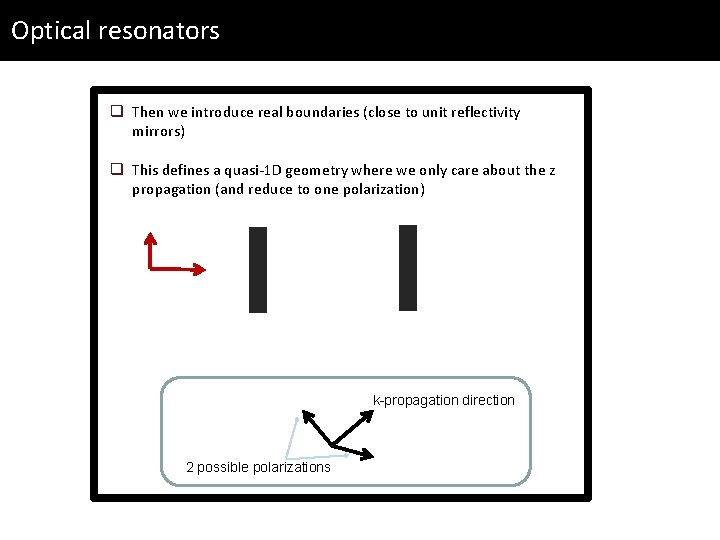
Optical resonators q Then we introduce real boundaries (close to unit reflectivity mirrors) q This defines a quasi-1 D geometry where we only care about the z propagation (and reduce to one polarization) k-propagation direction 2 possible polarizations

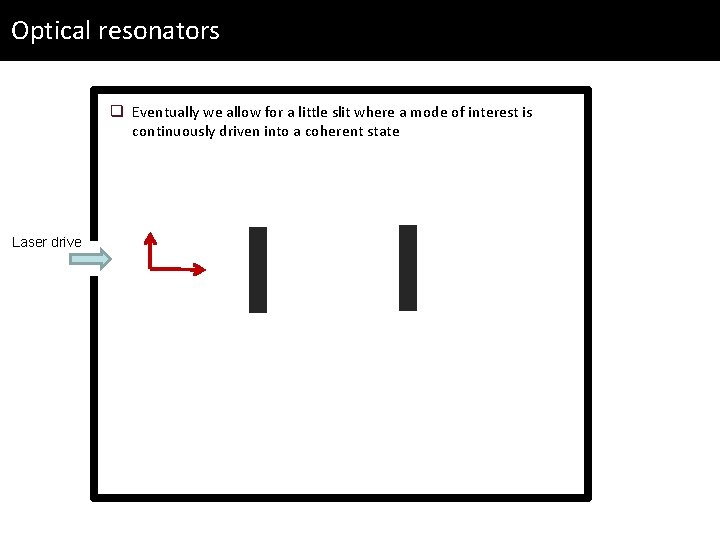
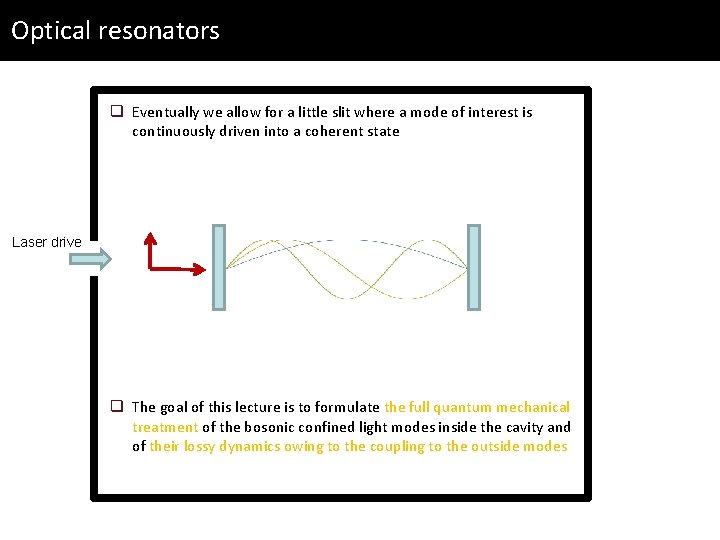
Optical resonators q Eventually we allow for a little slit where a mode of interest is continuously driven into a coherent state Laser drive

Optical resonators q Eventually we allow for a little slit where a mode of interest is continuously driven into a coherent state Laser drive q The goal of this lecture is to formulate the full quantum mechanical treatment of the bosonic confined light modes inside the cavity and of their lossy dynamics owing to the coupling to the outside modes

Optical resonators – classical treatment

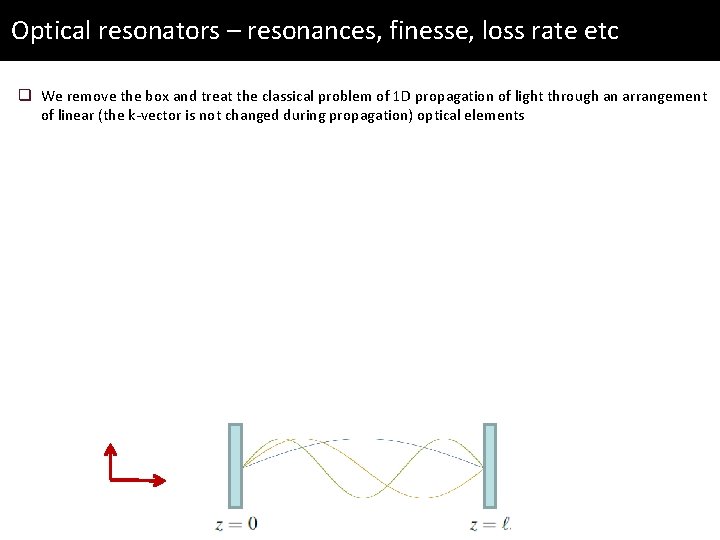
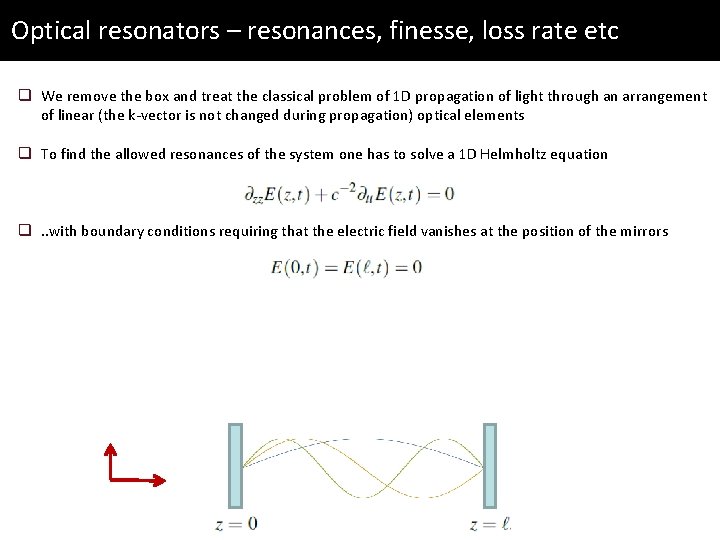
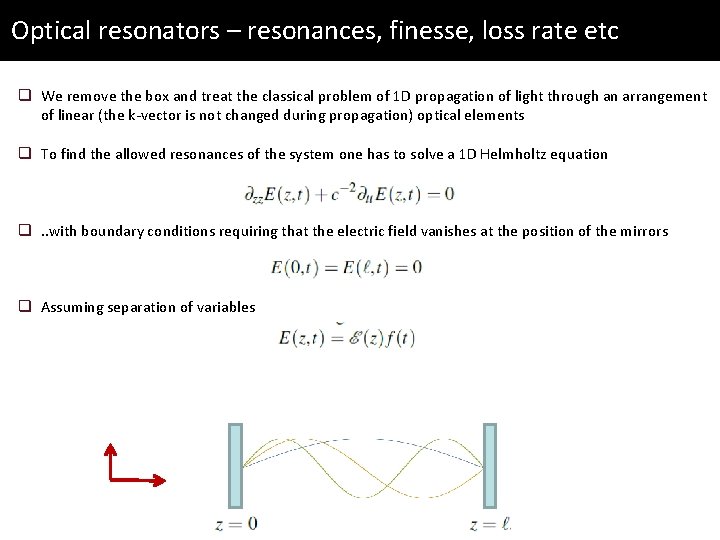
Optical resonators – resonances, finesse, loss rate etc q We remove the box and treat the classical problem of 1 D propagation of light through an arrangement of linear (the k-vector is not changed during propagation) optical elements

Optical resonators – resonances, finesse, loss rate etc q We remove the box and treat the classical problem of 1 D propagation of light through an arrangement of linear (the k-vector is not changed during propagation) optical elements q To find the allowed resonances of the system one has to solve a 1 D Helmholtz equation q. . with boundary conditions requiring that the electric field vanishes at the position of the mirrors

Optical resonators – resonances, finesse, loss rate etc q We remove the box and treat the classical problem of 1 D propagation of light through an arrangement of linear (the k-vector is not changed during propagation) optical elements q To find the allowed resonances of the system one has to solve a 1 D Helmholtz equation q. . with boundary conditions requiring that the electric field vanishes at the position of the mirrors q Assuming separation of variables

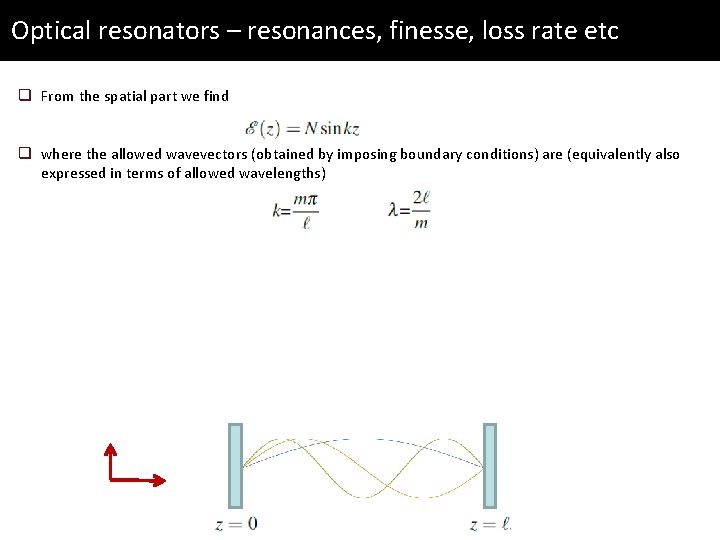
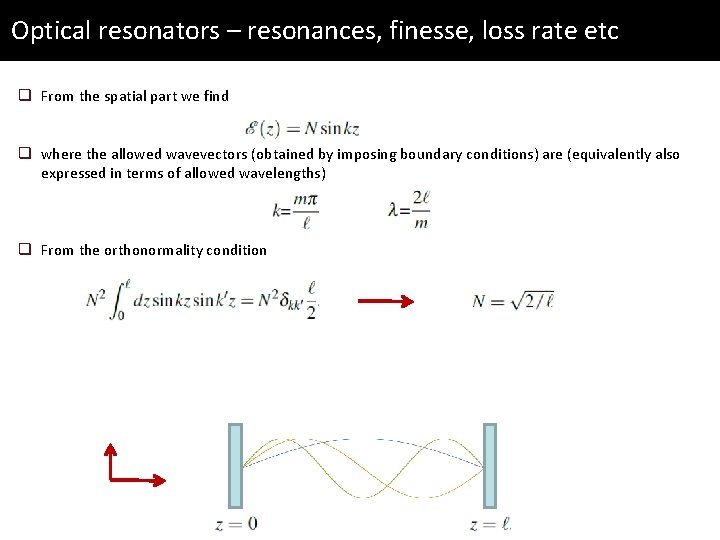
Optical resonators – resonances, finesse, loss rate etc q From the spatial part we find q where the allowed wavevectors (obtained by imposing boundary conditions) are (equivalently also expressed in terms of allowed wavelengths)

Optical resonators – resonances, finesse, loss rate etc q From the spatial part we find q where the allowed wavevectors (obtained by imposing boundary conditions) are (equivalently also expressed in terms of allowed wavelengths) q From the orthonormality condition

Optical resonators – resonances, finesse, loss rate etc q We found the allowed modes but now we move to assume imperfect mirrors (allowing tunneling of light to the outside of the cavity) q To this end we will use a transfer matrix formalism tailored to 1 D propagation

Optical resonators – resonances, finesse, loss rate etc q We found the allowed modes but now we move to assume imperfect mirrors (allowing tunneling of light to the outside of the cavity) q To this end we will use a transfer matrix formalism tailored to 1 D propagation q For a single reflector q One can obtain the relation above by solving the Helmholtz equation for a dielectric slab q In the absence of absorption

Optical resonators – resonances, finesse, loss rate etc q One starts with

Optical resonators – resonances, finesse, loss rate etc q One starts with q …and after a bit of work obtains

Optical resonators – resonances, finesse, loss rate etc q One starts with q …and after a bit of work obtains q A more convenient parametrization in terms of the susceptibility

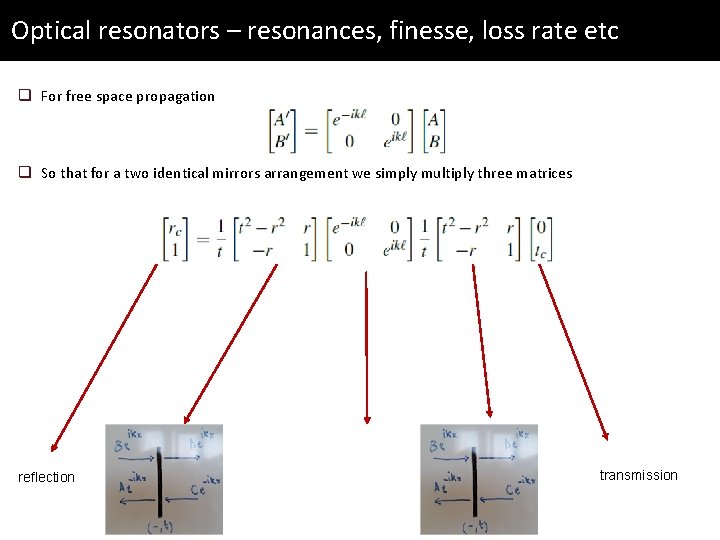
Optical resonators – resonances, finesse, loss rate etc q For free space propagation

Optical resonators – resonances, finesse, loss rate etc q For free space propagation q So that for a two identical mirrors arrangement we simply multiply three matrices reflection transmission

Optical resonators – resonances, finesse, loss rate etc q For free space propagation q So that for a two identical mirrors arrangement we simply multiply three matrices reflection transmission

Optical resonators – resonances, finesse, loss rate etc q Analyzing the transmission

Optical resonators – resonances, finesse, loss rate etc q Analyzing the transmission q …and the intensity transmission

Optical resonators – resonances, finesse, loss rate etc q Analyzing the transmission q …and the intensity transmission q Unity is reached when q One can approximate

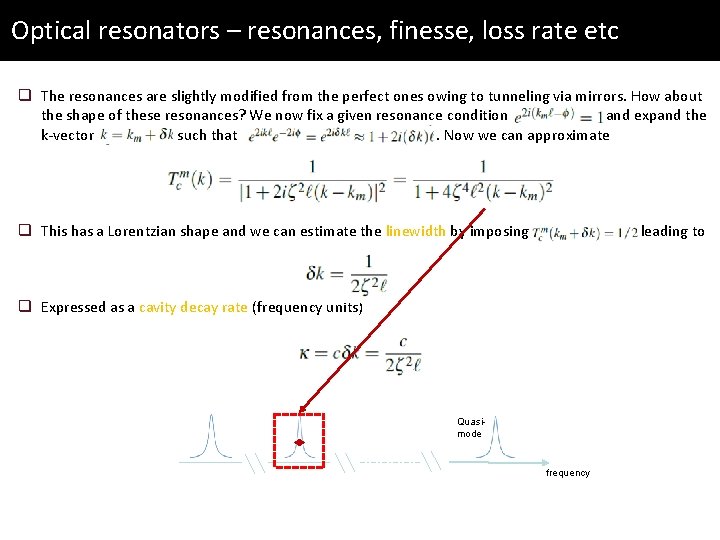
Optical resonators – resonances, finesse, loss rate etc q The resonances are slightly modified from the perfect ones owing to tunneling via mirrors. How about the shape of these resonances? We now fix a given resonance condition and expand the k-vector such that. Now we can approximate q This has a Lorentzian shape …

Optical resonators – resonances, finesse, loss rate etc q The resonances are slightly modified from the perfect ones owing to tunneling via mirrors. How about the shape of these resonances? We now fix a given resonance condition and expand the k-vector such that. Now we can approximate q This has a Lorentzian shape and we can estimate the linewidth by imposing q Expressed as a cavity decay rate (frequency units) leading to

Optical resonators – resonances, finesse, loss rate etc q The resonances are slightly modified from the perfect ones owing to tunneling via mirrors. How about the shape of these resonances? We now fix a given resonance condition and expand the k-vector such that. Now we can approximate q This has a Lorentzian shape and we can estimate the linewidth by imposing leading to q Expressed as a cavity decay rate (frequency units) Quasimode frequency

Optical resonators – resonances, finesse, loss rate etc q There a few other quantities defined in the literature (especially in the experimental world) q Finesse (number of round trips of a photon before escaping via the mirror tunneling)

Optical resonators – resonances, finesse, loss rate etc q There a few other quantities defined in the literature (especially in the experimental world) q Finesse (number of round trips of a photon before escaping via the mirror tunneling) q One can now re-express q Quality factor

Optical resonators – quantum treatment

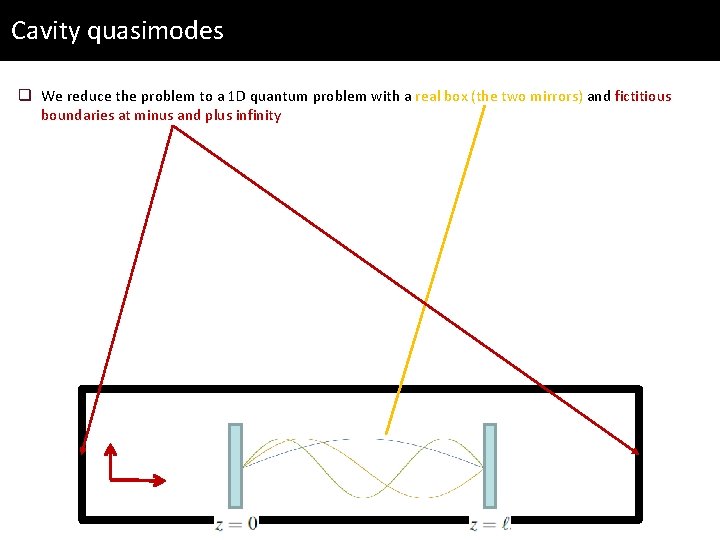
Cavity quasimodes q We reduce the problem to a 1 D quantum problem with a real box (the two mirrors) and fictitious boundaries at minus and plus infinity

Cavity quasimodes q We reduce the problem to a 1 D quantum problem with a real box (the two mirrors) and fictitious boundaries at minus and plus infinity q We follow the same quantization procedure as previously introduced (but with fixed boundary conditions) such that for a given cavity mode we have

Cavity quasimodes q We reduce the problem to a 1 D quantum problem with a real box (the two mirrors) and fictitious boundaries at minus and plus infinity q Similarly we describe the infinity of modes outside by keeping track of the k-vector and introducing bosonic operators to the left and right of the cavity

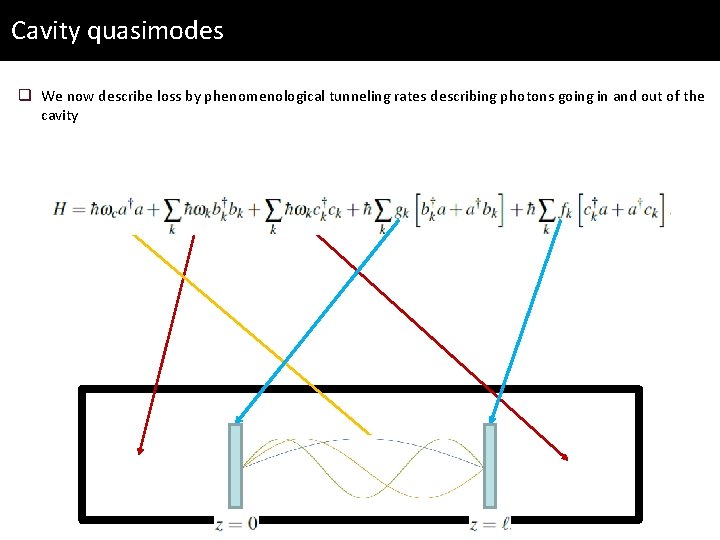
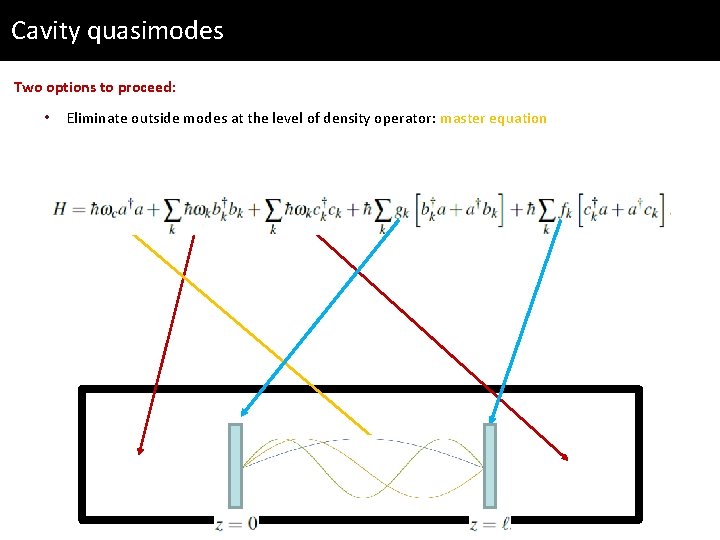
Cavity quasimodes q We now describe loss by phenomenological tunneling rates describing photons going in and out of the cavity

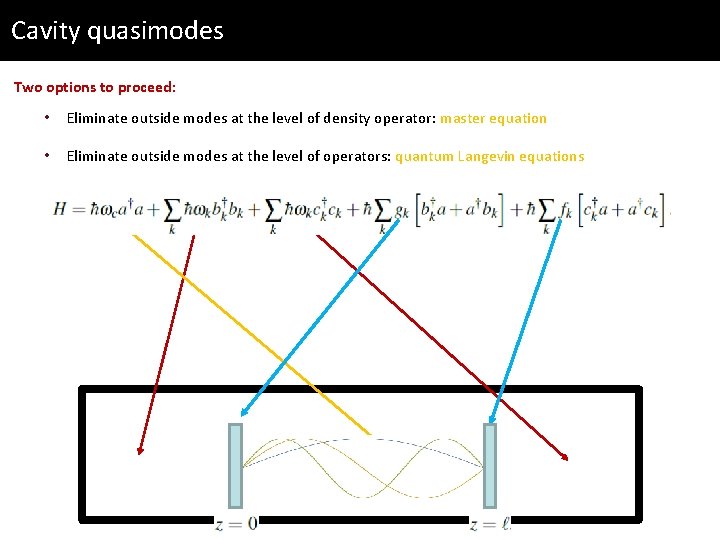
Cavity quasimodes Two options to proceed: • Eliminate outside modes at the level of density operator: master equation

Cavity quasimodes Two options to proceed: • Eliminate outside modes at the level of density operator: master equation • Eliminate outside modes at the level of operators: quantum Langevin equations

Quantum Langevin equations q We start by writing the Heisenberg equations of motion

Quantum Langevin equations q We start by writing the Heisenberg equations of motion q And formally integrate the outside modes

Quantum Langevin equations – decay rates q We obtain an integro-differential equation for the cavity mode

Quantum Langevin equations – decay rates q We obtain an integro-differential equation for the cavity mode

Quantum Langevin equations – decay rates q We obtain an integro-differential equation for the cavity mode q We perform a Markov approximation assuming that the tunneling rate is independent of k. Using and

Quantum Langevin equations – decay rates q We obtain an integro-differential equation for the cavity mode q We perform a Markov approximation assuming that the tunneling rate is independent of k. Using and leads to an effective loss of amplitude for the cavity annihilation operator …with the first integral simply

Quantum Langevin equations – input noise q We obtain an integro-differential equation for the cavity mode

Quantum Langevin equations – input noise q We obtain an integro-differential equation for the cavity mode q We define the following time dependent stochastic operators q With zero averages

Quantum Langevin equations – input noise q We obtain an integro-differential equation for the cavity mode q We define the following time dependent stochastic operators q With zero averages q And the following two-time correlations

Quantum Langevin equations – driving term q Finally we have the quantum Langevin equation for an undriven cavity mode

Quantum Langevin equations – driving term q Finally we have the quantum Langevin equation for an undriven cavity mode q Assuming that instead of vacuum we feed a coherent state through the left port

Quantum Langevin equations – driving term q Finally we have the quantum Langevin equation for an undriven cavity mode q Assuming that instead of vacuum we feed a coherent state through the left port q And we can rewrite the quantum Langevin equation with driving as q where we redefine the input noise with respect to the vacuum

Master equation for a bosonic cavity mode q Without details on the derivation (which is similar to the one performed for the spontaneous emission of a TLS) q The Hamiltonian contains the free part and the driving

Master equation to quantum Langevin equations translations * To convince yourself of the validity of the above expression start with the master equations and see if you reproduce the Langevin equation ** Do then the same thing for a TLS and be careful with the commutation relations for spin operators. The equations are more complicated for spin algebra than for bosonic algebra

…in the next class Quantum Langevin equations q Derivation of input output relations q Single sided versus double sided cavities q Solving the Langevin equations both in the time and frequency domain Cavity quantum electrodynamics with TLS q Rabi and Jaynes-Cummings light-matter Hamiltonians q Strong coupling, Purcell effect (modification of decay rate) and polaritons