Quantum Physics of LightMatter Interactions Lecturer Claudiu Genes

Quantum Physics of Light-Matter Interactions Lecturer: Claudiu Genes Max Planck Institute for the Science of Light (Erlangen, Germany) -- Lecture 6 -- Genes Research Group Cooperative Quantum Phenomena

From the last class q For a double-sided undriven cavity we have the following Langevin equation Laser drive

From the last class q For a double-sided undriven cavity we have the following Langevin equation q Laser driving is easily included Laser drive

From the last class q For a double-sided undriven cavity we have the following Langevin equation q Laser driving is easily included q This comes from assuming that an individual mode on the left is continuously driven into a coherent state Laser drive

From the last class q For a double-sided undriven cavity we have the following Langevin equation q Laser driving is easily included q This comes from assuming that an individual mode on the left is continuously driven into a coherent state q And we make a replacement (where the displaced noise operator is zero-averaged) Laser drive

From the last class q For a double-sided undriven cavity we have the following Langevin equation q Laser driving is easily included q The important properties of the input noise terms (zero average and white noise correlations) Laser drive

Single-sided cavity (simplified approach) q Let us consider that the right mirror is perfectly reflective (single sided cavity). We can easily write q …where we made the substitution and included all noise in the

Single-sided cavity (simplified approach) q Let us consider that the right mirror is perfectly reflective (single sided cavity). We can easily write q …where we made the substitution and included all noise in the q But we can also obtain this by folding a two-sided cavity into a single-sided one q The compound noise has the same properties total decay rate as and we need to redefine the

Solving a quantum Langevin equations – time domain q We start with the driven equation

Solving a quantum Langevin equations – time domain q We start with the driven equation q And first move into a rotating frame to eliminate the fast laser time evolution q We can formally integrate to get

Solving a quantum Langevin equations – time domain q We start with the driven equation q And first move into a rotating frame to eliminate the fast laser time evolution q We can formally integrate to get

Solving a quantum Langevin equations – time domain q We start with the driven equation q And first move into a rotating frame to eliminate the fast laser time evolution q We can formally integrate to get Transient solution to get

Solving a quantum Langevin equations – time domain q We start with the driven equation q And first move into a rotating frame to eliminate the fast laser time evolution q We can formally integrate to get Transient solution Steady state solution to get

Solving a quantum Langevin equations – time domain

Solving a quantum Langevin equations – time domain q We use (by pushing the initial condition back in time )

Solving a quantum Langevin equations – time domain q We use (by pushing the initial condition back in time ) q Which gives the steady state for the cavity mode amplitude q As expected we obtain a Lorentzian around the cavity resonance and with linewidth

Solving a quantum Langevin equations – time domain q We use (by pushing the initial condition back in time ) q Which gives the steady state for the cavity mode amplitude q As expected we obtain a Lorentzian around the cavity resonance and with linewidth q Notice that an usual failure in these calculation is to set derivatives to zero in steady state. This is not allowed as noise terms are quickly oscillating. Instead it is the noise that keeps comutators

Input-output relations q Tracing back to the derivation of the Langevin equation (for single sided cavity) q where the input noise is defined with respect to initial time operators (and notice that we keep classical drive amplitude within the input noise terms

Input-output relations q Tracing back to the derivation of the Langevin equation (for single sided cavity) q where the input noise is defined with respect to initial time operators (and notice that we keep classical drive amplitude within the input noise terms q Now we integrate with respect to a time in the future q And define similarly an output operator

Input-output relations q Tracing back to the derivation of the Langevin equation (for single sided cavity) q where the input noise is defined with respect to initial time operators (and notice that we keep classical drive amplitude within the input noise terms q Now we integrate with respect to a time in the future q And define similarly an output operator q From the two different forms of the Langevin equations we obtain a simple relation

Cavity tranmission for double-sided setup q Let us consider an incoming field of amplitude q We can connect the incoming, reflected and transmitted parts via the input-output relations at each mirror (assuming both mirrors have loss ) Notice the connection as used in the transfer matrix formalism

Cavity tranmission for double-sided setup q Let us consider an incoming field of amplitude q We can connect the incoming, reflected and transmitted parts via the input-output relations at each mirror (assuming both mirrors have loss ) Notice the connection as used in the transfer matrix formalism q Using the result from a few slides back q …we have

TLS inside an optical resonator

The Rabi Hamiltonian q As previously written for the fictitious quantization box, before any rotating wave approximations and for a single cavity mode we can write

The Rabi Hamiltonian q As previously written for the fictitious quantization box, before any rotating wave approximations and for a single cavity mode we can write q The coupling strength now depends also on the positioning along the standing wave describing the spatial part of the cavity mode

The Rabi Hamiltonian q As previously written for the fictitious quantization box, before any rotating wave approximations and for a single cavity mode we can write q The coupling strength now depends also on the positioning along the standing wave describing the spatial part of the cavity mode q The model is solvable (however solution is tedious) – see D. Braak, Integrability of the Rabi Model, Phys. Rev. Lett. 107, 100401 (2011)

The Rabi Hamiltonian q As previously written for the fictitious quantization box, before any rotating wave approximations and for a single cavity mode we can write q The coupling strength now depends also on the positioning along the standing wave describing the spatial part of the cavity mode q The model is solvable (however solution is tedious) – see D. Braak, Integrability of the Rabi Model, Phys. Rev. Lett. 107, 100401 (2011) q Easy solution for ground state eigenstates in the degenerate case where

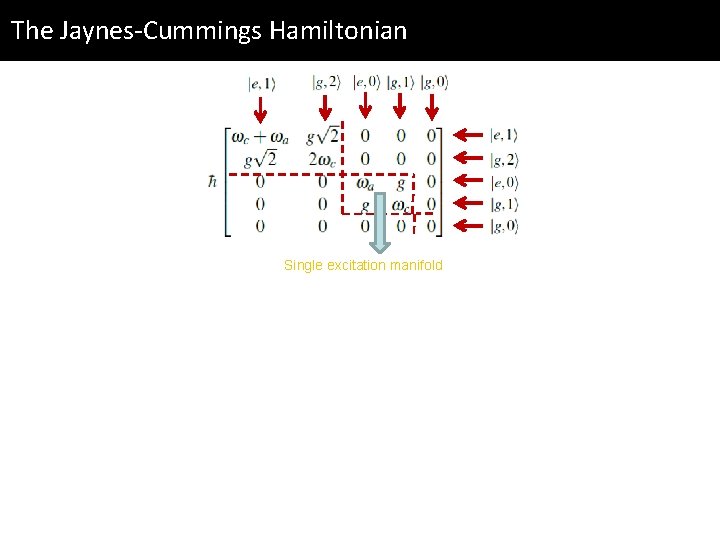
The Jaynes-Cummings Hamiltonian q In a vast majority of situations we have approximation which allows for a rotating wave

The Jaynes-Cummings Hamiltonian q In a vast majority of situations we have approximation which allows for a rotating wave q This is an excitation conserving Hamiltonian. We use the infinite basis the matrix elements and compute

The Jaynes-Cummings Hamiltonian q In a vast majority of situations we have approximation which allows for a rotating wave q This is an excitation conserving Hamiltonian. We use the infinite basis the matrix elements and compute

The Jaynes-Cummings Hamiltonian q In a vast majority of situations we have approximation which allows for a rotating wave q This is an excitation conserving Hamiltonian. We use the infinite basis the matrix elements and compute Block diagonal

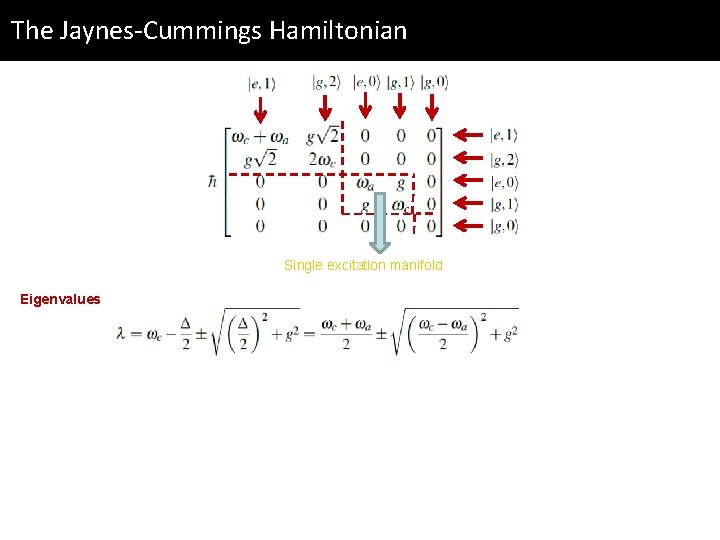
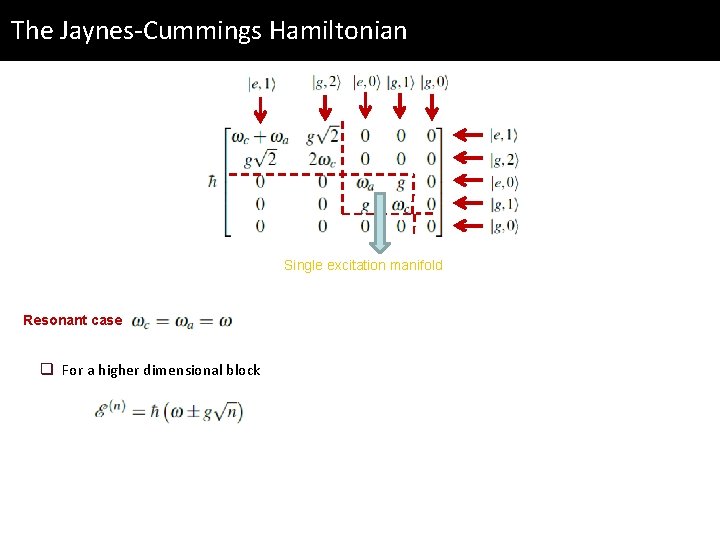
The Jaynes-Cummings Hamiltonian Single excitation manifold

The Jaynes-Cummings Hamiltonian Single excitation manifold Eigenvalues

The Jaynes-Cummings Hamiltonian Single excitation manifold Eigenvalues Resonant case !! Polaritons – hybrid light-matter quantum states

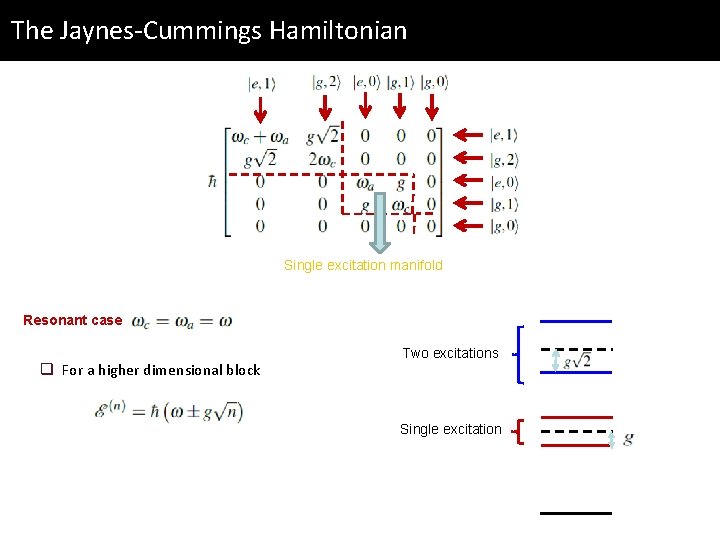
The Jaynes-Cummings Hamiltonian Single excitation manifold Resonant case q For a higher dimensional block

The Jaynes-Cummings Hamiltonian Single excitation manifold Resonant case q For a higher dimensional block Two excitations Single excitation

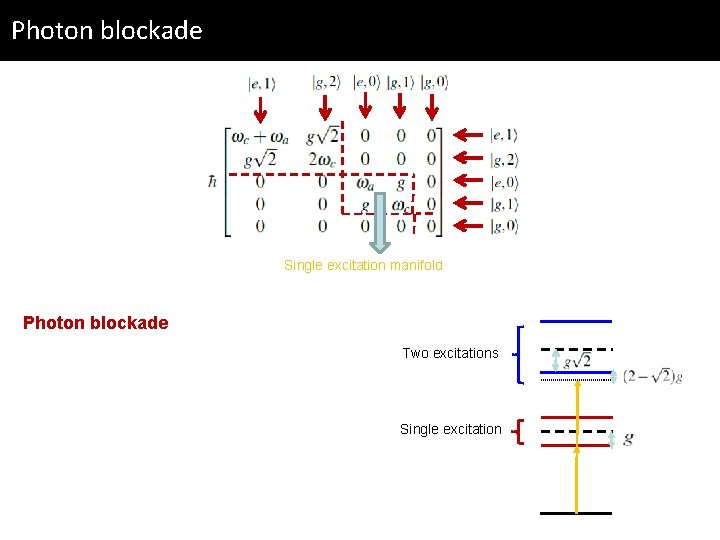
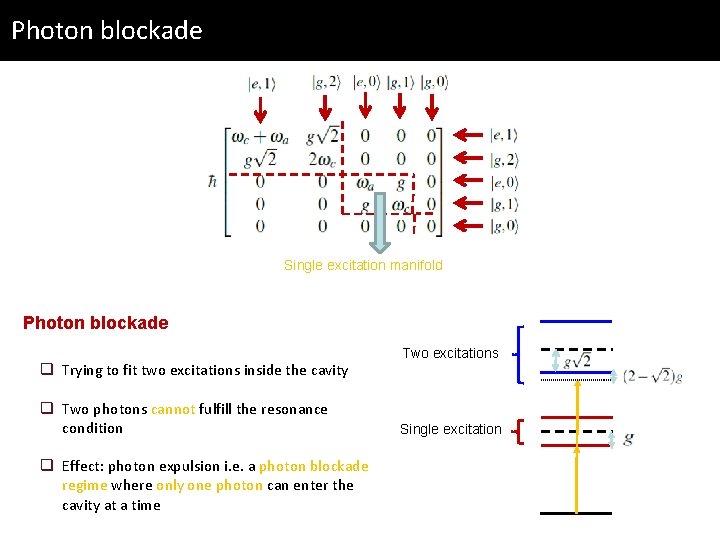
Photon blockade Single excitation manifold Photon blockade Two excitations Single excitation

Photon blockade Single excitation manifold Photon blockade q Trying to fit two excitations inside the cavity q Two photons cannot fulfill the resonance condition q Effect: photon expulsion i. e. a photon blockade regime where only one photon can enter the cavity at a time Two excitations Single excitation

The polariton transformation Upper and lower polaritons q Define polariton operators Single excitation

The polariton transformation Upper and lower polaritons q Define polariton operators q It is easy to see that they bring us from the ground state to the polaritonic states: for example Single excitation

The polariton transformation Upper and lower polaritons q Define polariton operators q It is easy to see that they bring us from the ground state to the polaritonic states: for example q Diagonalization of the Hamiltonian: working out the math we have Single excitation

The polariton transformation Upper and lower polaritons q Define polariton operators q It is easy to see that they bring us from the ground state to the polaritonic states: for example q Diagonalization of the Hamiltonian: working out the math we have q This also diagonalizes the Lindblad terms: each polariton decay independently with its own collapse operator and equal rates Single excitation

Cavity-TLS optical linear response Low excitation limit – optical response of the cavity q We look at the complete problem with Hamiltonian q and two Lindblad terms

Cavity-TLS optical linear response Low excitation limit – optical response of the cavity q We look at the complete problem with Hamiltonian q and two Lindblad terms q We would like to derive a set of equations of motion for amplitudes

Cavity-TLS optical linear response Low excitation limit – optical response of the cavity q We look at the complete problem with Hamiltonian q and two Lindblad terms q We would like to derive a set of equations of motion for amplitudes q These equations are not closed as the population difference operator comes in

Cavity-TLS optical linear response Low excitation limit – optical response of the cavity q We look at the complete problem with Hamiltonian q and two Lindblad terms q We would like to derive a set of equations of motion for amplitudes q These equations are not closed as the population difference operator comes in q Approximation: the low excitation regime

Cavity-TLS optical linear response Low excitation limit – optical response of the cavity q Simplified linear set of first order differential equations

Cavity-TLS optical linear response Low excitation limit – optical response of the cavity q Simplified linear set of first order differential equations q Analysis of eigenvalues (real and imaginary parts) leads to

Cavity-TLS optical linear response Low excitation limit – optical response of the cavity q Simplified linear set of first order differential equations q Analysis of eigenvalues (real and imaginary parts) leads to q The onset of the strong coupling regime (splitting of eigenfrequencies)

Cavity-TLS optical linear response – strong coupling Low excitation limit – optical response of the cavity q Simplified linear set of first order differential equations q Analysis of eigenvalues (real and imaginary parts) leads to q The onset of the strong coupling regime (splitting of eigenfrequencies)

Cavity-TLS optical linear response Low excitation limit – optical response of the cavity q Simplified linear set of first order differential equations q Analysis of eigenvalues (real and imaginary parts) leads to q The onset of the strong coupling regime (splitting of eigenfrequencies) q Steady state values

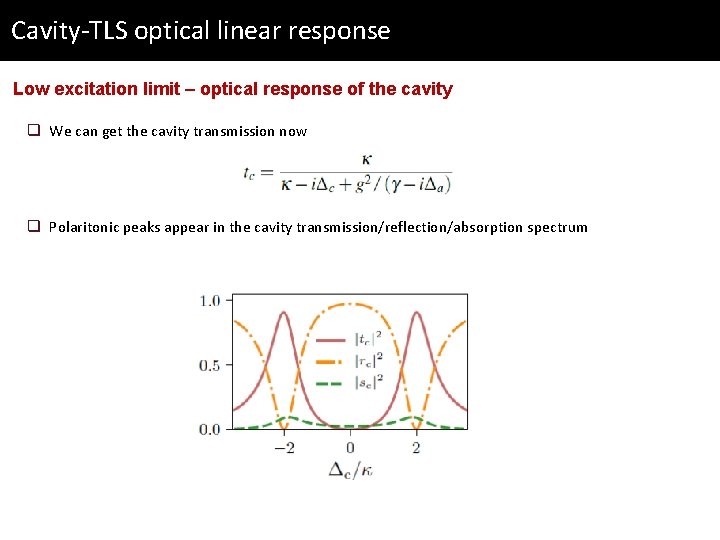
Cavity-TLS optical linear response Low excitation limit – optical response of the cavity q We can get the cavity transmission now q Polaritonic peaks appear in the cavity transmission/reflection/absorption spectrum

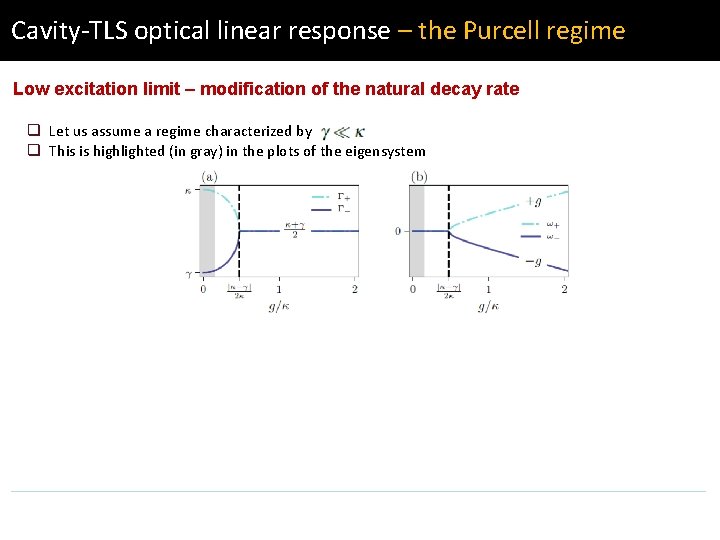
Cavity-TLS optical linear response – the Purcell regime Low excitation limit – modification of the natural decay rate q Let us assume a regime characterized by q This is highlighted (in gray) in the plots of the eigensystem

Cavity-TLS optical linear response – the Purcell regime Low excitation limit – modification of the natural decay rate q Let us assume a regime characterized by q This is highlighted (in gray) in the plots of the eigensystem q Assume steady state for the cavity field* and obtain to lead to which could be plugged back in *perform a simple numerical simulation of the time dynamics of such system under the conditions above to convince yourselves that the system indeed achieves steady state very quickly for the cavity mode

Cavity-TLS optical linear response – the Purcell regime Low excitation limit – modification of the natural decay rate q Let us assume a regime characterized by q This is highlighted (in gray) in the plots of the eigensystem q Assume steady state for the cavity field* and obtain to lead to which could be plugged back in Purcell effect *perform a simple numerical simulation of the time dynamics of such system under the conditions above to convince yourselves that the system indeed achieves steady state very quickly for the cavity mode

Cavity-TLS optical linear response – the Purcell regime Low excitation limit – modification of the natural decay rate q Let us assume a regime characterized by q This is highlighted (in gray) in the plots of the eigensystem q Assume steady state for the cavity field* and obtain to lead to which could be plugged back in Purcell effect q Increase by a factor where the cooperativity is defined as *perform a simple numerical simulation of the time dynamics of such system under the conditions above to convince yourselves that the system indeed achieves steady state very quickly for the cavity mode