Performance analysis of algorithms What is Programming Programming

Performance analysis of algorithms

What is Programming? Programming is to represent data and Data Structures solve the problem using the data. Algorithms 2

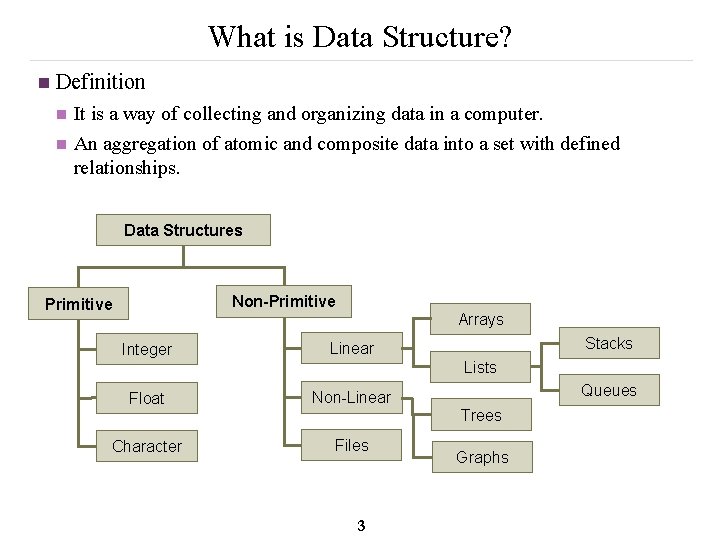
What is Data Structure? n Definition n n It is a way of collecting and organizing data in a computer. An aggregation of atomic and composite data into a set with defined relationships. Data Structures Non-Primitive Arrays Integer Linear Float Non-Linear Character Files Stacks Lists 3 Queues Trees Graphs

What is Algorithm? Definition: a finite set of instructions that should satisfy the following: n n n Input: zero or more inputs Output: at least one output Definiteness: clear and unambiguous instructions Finiteness: terminating after a finite number of steps Effectiveness (Machine-executable): enough to be carried out In computational theory, algorithm and program are different n n Program does not satisfy 4): eg. OS 4

Algorithm Specification n How to express algorithms n n High-level description n Natural language n Graphic representation, e. g. , flowcharts n Pseudocode: informal language-dependent description Implementation description n C, C++, Java, and etc. 5

Natural Language vs. Graphic Chart n Example: Selection Sort From those integers that are currently unsorted, find the smallest value. Place it next in the sorted list[0] 6 2 2 2 list[1] 5 5 3 3 list[2] 3 3 5 4 4 4 list[3] 4 4 4 5 5 5 list[4] 2 6 6 6 Step 1 Step 2 Step 3 Step 4 Step 5 Step 6 6

Pseudocode (C-like Language) n Example: Selection Sort for (i=0; i<n; i++) { Examine numbers in list[i] to list[n-1]. Suppose that the smallest integer is at list[min]. Interchange list[i] and list[min]. } 7

Implementation in C n Example: Selection Sort void sort(int list[], int n) { int i, j, min; for (i = 0; i < n - 1; i++) { min = i; for (j = i + 1; j < n; j++) if (list[j] < list[min]) min = j; SWAP(list[i], list[min]); } } 8

Algorithm Analysis n How do we evaluate algorithms? n n Does the algorithm use the storage efficiently? Is the running time of the algorithm acceptable for the task? void search(int arr[], int len, int target) { for (int i = 0; i < len; i++) { if (arr[i] == target) return i; } return -1 } n Performance analysis n Estimating machine-independent time and space Space complexity: an amount of memory needed Time complexity: an amount of time taken for an algorithm to finish 9

Space Complexity n Definition n n (machine-independent) space required by an algorithm Example int abc(int a, int b, int c) { return a + b*c + 4. 0; } char* give_me_memory(int n) { char *p = malloc(n); return p; } 10

Space Complexity n What is better for space complexity? float sum(float *list, int n) { float tempsum = 0; for (int i = 0; i < n; i++) tempsum += *(list + i); return tempsum; } float rsum(float *list, int n) { if (n > 0) return rsum(list, n - 1) + list[n - 1]; else return 0; } 11

Time Complexity n Definition n n (machine-independent) time required by an algorithm Time is not easy to estimate! 10 Additions, 10 subtractions, 10 multiplications Þ 10 Ca+10 Cs+10 Cm Ca: time for one addition Cs: time for one subtraction Cm: time for one multiplication n Alternative n Count the number of program steps instead of time. 10 Additions, 10 subtractions, 10 multiplications Þ 30 steps 12

Time Complexity n Program steps n Syntactically or semantically meaningful program segment whose execution time is independent of the number of inputs n Any one basic operation Þ one step n n +, -, *, /, assignment, jump, comparison, etc. Any combination of basic operations Þ one step n +=, *=, /=, (a+c*d), etc. 13

Time Complexity n Example int abc(int a, int b, int c) { return a + b*c + 4. 0; } void add(int a[][MAX_SIZE], . . . ) { int i, j; for (i = 0; i < rows; i++) for (j = 0; j < cols; j++) c[i][j] = a[i][j] + b[i][j]; } 14

Time Complexity n What is better for time complexity? float sum(float *list, int n) { float tempsum = 0; for (int i = 0; i < n; i++) tempsum += *(list + i); return tempsum; } float rsum(float *list, int n) { if (n > 0) return rsum(list, n - 1) + list[n - 1]; else return 0; } 15

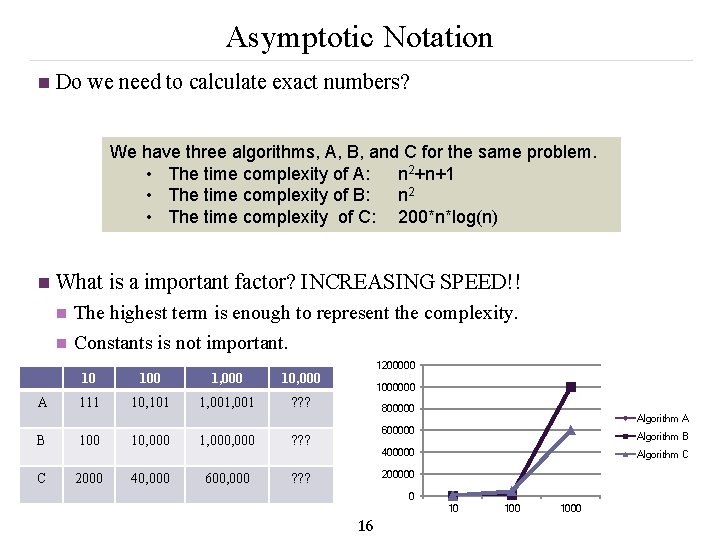
Asymptotic Notation n Do we need to calculate exact numbers? We have three algorithms, A, B, and C for the same problem. • The time complexity of A: n 2+n+1 • The time complexity of B: n 2 • The time complexity of C: 200*n*log(n) n What is a important factor? INCREASING SPEED!! n n A B C The highest term is enough to represent the complexity. Constants is not important. 10 100 1, 000 10, 000 111 10, 101 1, 001 ? ? ? 100 2000 10, 000 40, 000 1, 000 600, 000 1200000 1000000 800000 Algorithm A 600000 ? ? ? Algorithm B 400000 Algorithm C 200000 ? ? ? 0 10 16 1000

Asymptotic Notation n What is better? n (10 n+10) vs. n (2000 n+3) vs. (nlogn+1000) n (n 3 ) vs. (0. 01 n 2+10) (10 n 2+1000000 n) Simple rule: 1. Ignore any constants. 2. Compare only the term of the highest order. 17

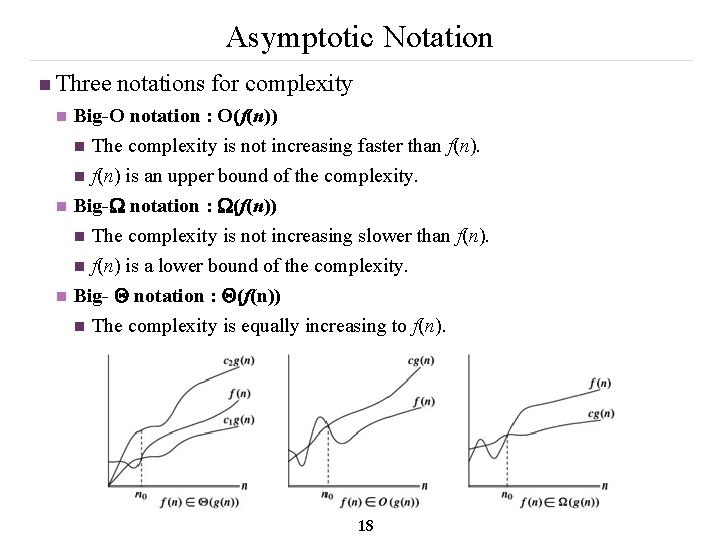
Asymptotic Notation n Three notations for complexity n n n Big-O notation : O(f(n)) n The complexity is not increasing faster than f(n) is an upper bound of the complexity. Big- notation : (f(n)) n The complexity is not increasing slower than f(n) is a lower bound of the complexity. Big- notation : (f(n)) n The complexity is equally increasing to f(n). 18

Big-O Notation n Definition f(n) = (g(n)) f(n) is not increasing faster than g(n) For a large number no, c*g(n) will be larger than f(n) There exist positive constants c and no such that f(n) £ c*g(n) for all n > no n Example n 3 n + log n + 2 = (n), because 3 n + log n + 2 £ 5 n for n ³ 2 n 10 n 2 + 4 n + 2 = (n 4), because 10 n 2 + 4 n + 2 £ 10 n 4 for n ³ 2 19

Example: Asymptotic Notation n Three asymptotic notations for space complexity float sum(float *list, int n) { float tempsum = 0; for (int i = 0; i < n; i++) tempsum += *(list + i); return tempsum; } (1) 16 bytes O(1) float rsum(float *list, int n) { if (n > 0) return rsum(list, n - 1) + list[n - 1]; else return 0; } 20 8*n bytes (n) O(n)

Example: Asymptotic Notation n Three asymptotic notations for time complexity float sum(float *list, int n) { float tempsum = 0; for (int i = 0; i < n; i++) tempsum += *(list + i); return tempsum; } (n) 2 n+3 O(n) void add(int a[][MAX_SIZE], . . . ) { int i, j; 2*r*c + 2*r + 1 for (i = 0; i < r; i++) for (j = 0; j < c; j++) c[i][j] = a[i][j] + b[i][j]; } 21 (r*c) O(r*c)

Discussion: Asymptotic Notation n Big-O notation is widely used. n n n Big- notation is the most informative, but the exact value is hard to know. Big- notation is the least informative. Why? Big-O notation is good for rough description. There is algorithm A. The exact complexity is very hard to evaluate. However, we know that n 2 £ complexity £ n 3. Then, we can say the complexity is O(n 3). 22

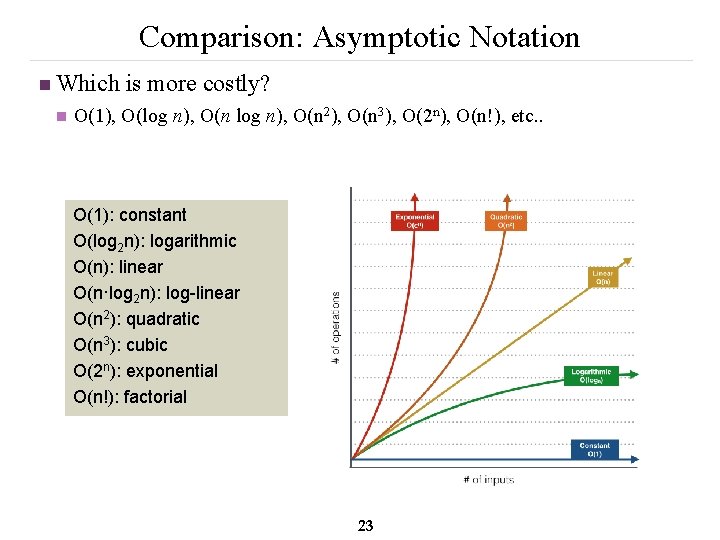
Comparison: Asymptotic Notation n Which is more costly? n O(1), O(log n), O(n 2), O(n 3), O(2 n), O(n!), etc. . O(1): constant O(log 2 n): logarithmic O(n): linear O(n·log 2 n): log-linear O(n 2): quadratic O(n 3): cubic O(2 n): exponential O(n!): factorial 23

Guideline for Asymptotic Analysis n Loops n The number of iterations * the running time of the statements inside the loop // executes n times for (int i = 0; i < n; i++) m = m + 1; // constant time, c // Total time = c * n = O(n) // outer loop executed n times for (int i = 0; i < n; i++) // inner loop executed n times for (int j = 0; j < n; j++) m = m + 1; // constant time, c // Total time = c * n = O(n 2) 24

Guideline for Asymptotic Analysis n Consecutive statements n Add the time complexities of each statement. // executes n times for (int i = 0; i < n; i++) m = m + 1; // constant time, c 1 // outer loop executed n times for (int i = 0; i < n; i++) // inner loop executed n times for (int j = 0; j < n; j++) k = k + 1; // constant time, c 2 // Total time = c 1 * n + c 2 * n 2 = O(n 2) 25

Guideline for Asymptotic Analysis n If-then-else statements n Consider the worst-case running time among the if, else-if, or else part (whichever is the larger). // executes n times if (len > 0) for (int i = 0; i < n; i++) m = m + 1; // constant time, c 1 else { // outer loop executed n times for (int i = 0; i < n; i++) if (i > 0) k = k + 2 // constant time, c 2 else // inner loop executed n times for (int j = 0; j < n; j++) k = k + 1; // constant time, c 3 } // Total time = n * c 3 = O(n 2) 26

Guideline for Asymptotic Analysis n Logarithmic complexity n An algorithm is O(log n) if it takes a constant time to cut the problem size by a fraction (usually by ½). // At kth step, 2 k = n and come out of loop. for (int i = 1; i < n; i*=2) m = m + 1; // constant time, c // Because k = log 2 n, total time = O(log n) // The same condition holds for decreasing sequence. for (int i = n; i > 0; i/=2) m = m + 1; // constant time, c // Because k = log 2 n, total time = O(log n) 27

Recursion

What is Recursion? n Definition n A repetitive process in which an algorithm calls itself #include <stdio. h> void Recursive(int n) { // Base case: termination condition! if (n == 0) return; printf("Recursive call: %dn", n); Recursive(n - 1); } 29

Example: Summing from 1 to n n Iterative vs. Recursive programming int sum(int n) { int sum = 0; for (int i = 0; i < n; i++) sum = sum + i; return sum; } int rsum(int n) { if (n == 0) return 0; else return rsum(n - 1) + n; } 30

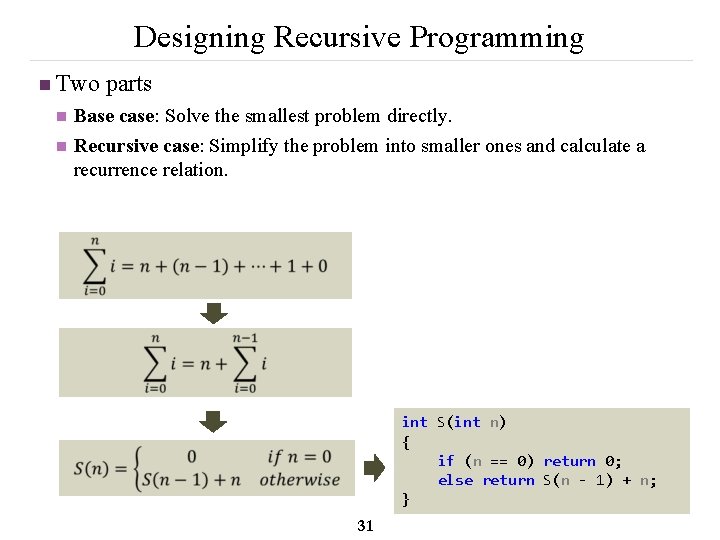
Designing Recursive Programming n Two parts n n Base case: Solve the smallest problem directly. Recursive case: Simplify the problem into smaller ones and calculate a recurrence relation. int S(int n) { if (n == 0) return 0; else return S(n - 1) + n; } 31

Function Call/Return n Is it a correct code? n Stack overflow: Eventually halt when runs out of (stack) memory. void Recursive(int n) { printf("Recursive call: %dn", n); Recursive(n - 1); } void Recursive(int n) { // Base case: termination condition! if (n == 0) return; else { printf("Recursive call: %dn", n); Recursive(n - 1); } } 32

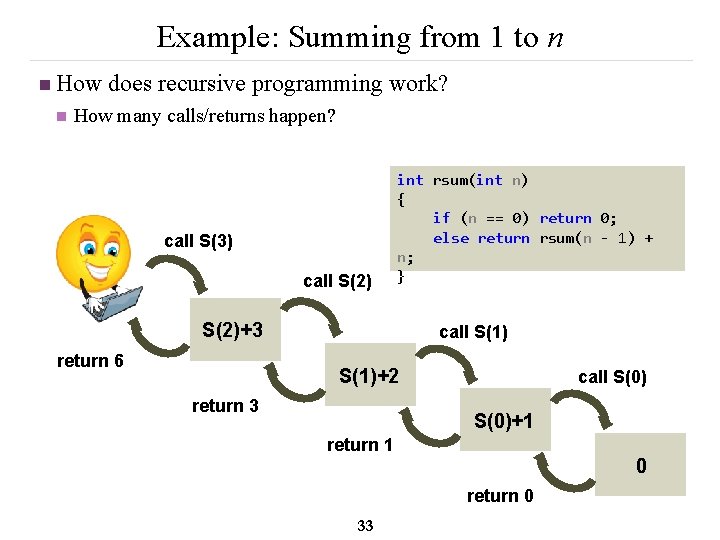
Example: Summing from 1 to n n How does recursive programming work? n How many calls/returns happen? call S(3) call S(2) int rsum(int n) { if (n == 0) return 0; else return rsum(n - 1) + n; } S(2)+3 return 6 call S(1)+2 return 3 call S(0)+1 return 1 0 return 0 33

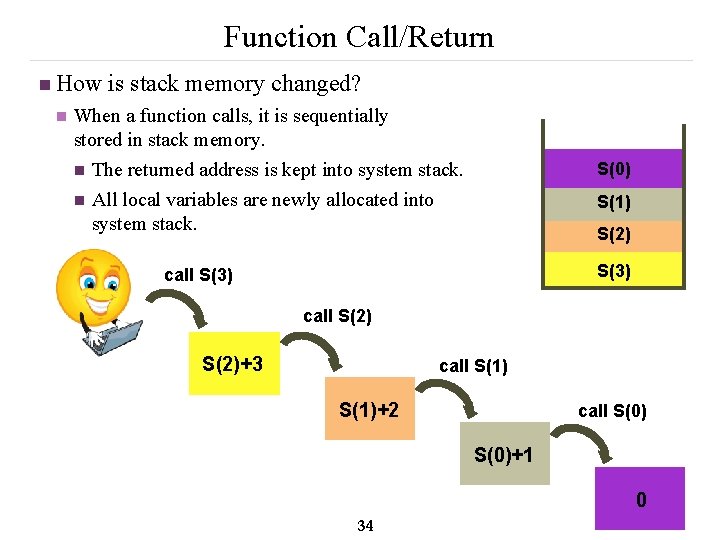
Function Call/Return n How is stack memory changed? n When a function calls, it is sequentially stored in stack memory. n The returned address is kept into system stack. n All local variables are newly allocated into system stack. S(0) S(1) S(2) S(3) call S(2)+3 call S(1)+2 call S(0)+1 0 34

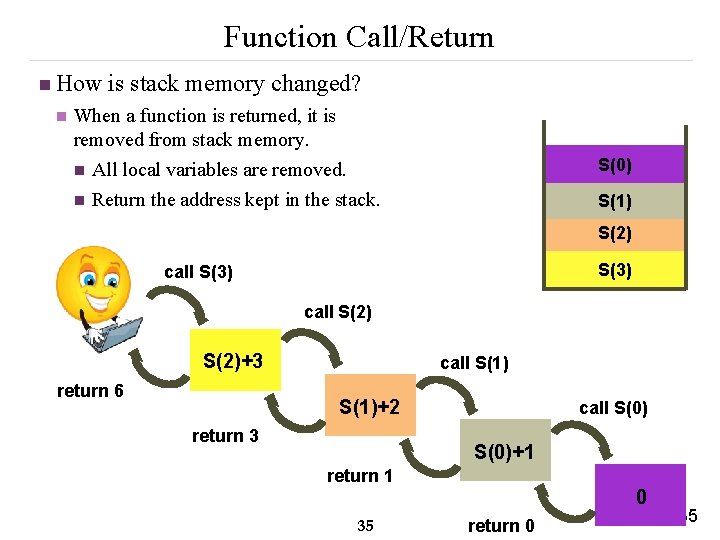
Function Call/Return n How is stack memory changed? n When a function is returned, it is removed from stack memory. n All local variables are removed. n Return the address kept in the stack. S(0) S(1) S(2) S(3) call S(2)+3 return 6 call S(1)+2 return 3 call S(0)+1 return 1 0 35 return 0 35

Recursion vs. Iteration n n n n Terminate when a condition is proven to be false. Each iteration does NOT require extra memory. Some iterative solutions may not be as obvious as recursive solutions. Recursion n Terminate when a base case is reached. Each recursive call requires extra space on stack memory. Some solutions are easier to formulate recursively. 36

Summing Multiples of Three n Calculate the sum of all multiples of three from 0 to n. int sum(int n) { int sum = 0; for (int i = 0; i <= n; i+=3) sum = sum + i; return sum; } int rsum(int n) { if (n == 0) return 0; else if (n % 3 != 0) return rsum(n – n % 3); else return rsum(n - 3) + n; } 37

Finding Maximum Number n Search the maximum number in array. int find. Max(int* arr, int n) { int max = arr[0]; for (int i = 1; i < n; i++) { if (arr[i] > max) max = arr[i]; } return max; } 38

Finding Maximum Number n Search the maximum number in array. int rfind. Max(int* arr, int n) { if (n == 1) return arr[0]; else { int max = rfind. Max(arr, n - 1); if (max < arr[n - 1]) return arr[n - 1]; else return max; } } 39

Printing Reverse String n Print a string in a reverse manner. n rprint("abc") cba, rprint("2 a 1 bc") cb 1 a 2 void rprint(char* s, int n) { for (int i = n - 1; i >= 0; i--) printf("%c", s[i]); } void rrprint(char* s, int n) { if (n == 0) return; else { printf("%c", s[n - 1]); return rrprint(s, n - 1); } } 40

Printing Binary Number n Print a binary number using recursion. n n n Note: Input a positive integer only. binary(1) 1, binary(3) 11 binary(10) 1010, binary(109) 1101101 void binary(int n) { if (n == 0) return; else { binary(n / 2); printf("%d", n % 2); } } 41

Calculating the Power of X n Iterative vs. recursive programming int power(int x, int n) { int pow = 1; for (int i = 0; i < n; i++) pow *= x; return pow; } int rpower(int x, int n) { if (n == 0) return 1; else return x * rpower(x, n - 1); } 42

Calculating the Power of X n int rpower(int x, int n) { if (n == 0) return 1; else return x * rpower(x, n - 1); } int rpower 2(int x, int n) { if (n == 0) return 1; else if (n % 2 == 0) { int m = rpower 2(x, n / 2); return m * m; } else return x * rpower 2(x, n - 1); } 43

Calculating Fibonacci Numbers n Every number is the sum of two preceding ones. n 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … int fibo(int n) { if (n == 1 || n == 2) return 1; else { int prev = 1, cur = 1, next = 1; for (int i = 3; i <= n; i++) { prev = cur, cur = next; next = prev + cur; } return next; } } int rfibo(int n) { if (n == 1 || n == 2) return 1; else return rfibo(n - 1) + rfibo(n - 2); } 44

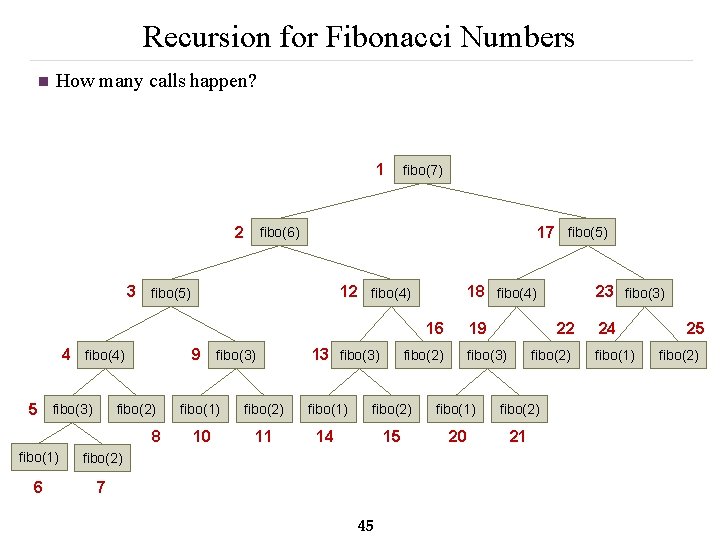
Recursion for Fibonacci Numbers n How many calls happen? 1 fibo(7) 2 fibo(6) 17 fibo(5) 3 fibo(5) 12 fibo(4) 18 fibo(4) 16 9 fibo(3) 4 fibo(4) 5 fibo(3) fibo(2) 8 fibo(1) fibo(2) 6 7 13 fibo(3) 19 fibo(2) 22 fibo(3) fibo(2) fibo(1) fibo(2) 10 11 14 15 20 21 45 23 fibo(3) 24 fibo(1) 25 fibo(2)

Binary Search using Recursion n Compare the median value in search space to the target value. n n Can eliminate half of the search space at each step. It will eventually be left with a search space consisting of a single element. int bsearch(int arr[], int low, int high, int target) { if (low > high) return -1; else { int mid = (low + high) / 2; if (target == arr[mid]) return (mid); else if (target < arr[mid]) bsearch(arr, low, mid - 1, target); else bsearch(arr, mid + 1, high, target); } } 46

Time Complexity for Recursion n How to calculate time complexity for recursion n T(n): the maximum amount of time taken on input of size n int S(int n) { if (n == 0) return 0; else return S(n - 1) + n; } n Formulate a recurrence relation with sub-problems. …… 47

Time Complexity for Recursion n Time complexity for binary search int bsearch(int arr[], int low, int high, int target) { if (low > high) return -1; else { int mid = (low + high) / 2; if (target == arr[mid]) return (mid); else if (target < arr[mid]) bsearch(arr, low, mid - 1, target); else bsearch(arr, mid + 1, high, target); } } 48

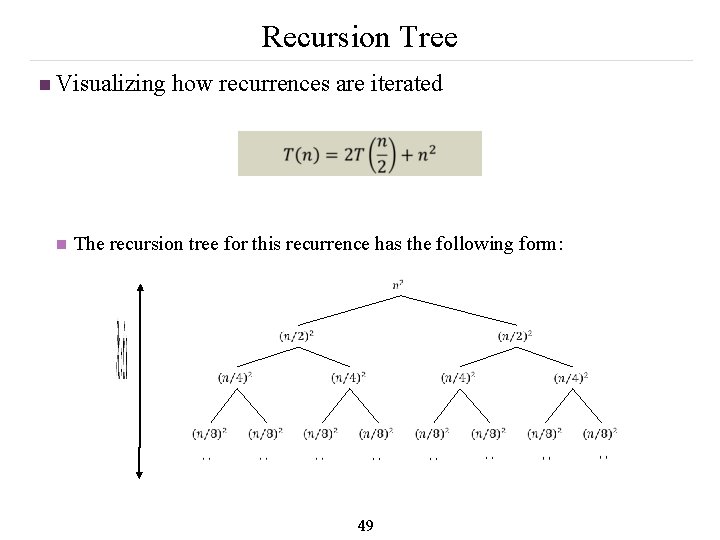
Recursion Tree n Visualizing how recurrences are iterated The recursion tree for this recurrence has the following form: 49 n

Recursion Tree n In the recursion tree, 50 n The depth of the tree does not really matter. The amount of work at each level is decreasing so quickly that the total is only a constant factor more than the root. n

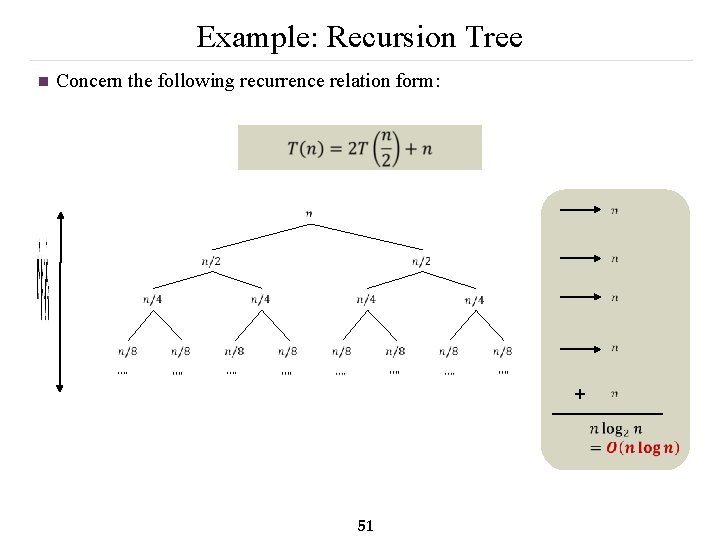
Example: Recursion Tree n Concern the following recurrence relation form: + 51

Master Theorem n 52

Example: Master Theorem n 53

Tail Recursion n It is a subroutine call performed as the final action of a function n Tail-call optimization: The current function is no longer needed and can thus be replaced by the tail-call function. rsum(4) rsum(3) + 4 (rsum(2) + 3) + 4 ((rsum(1) + 2) + 3) + 4 (((rsum(0) + 1) + 2) + 3) + 4 int rsum(int n) { if (n == 0) return 0; else return rsum(n - 1) + n; } int rsum 2(int n, int sum) { if (n == 0) return sum; else return rsum 2(n - 1, sum + n); } rsum 2(4, 0) rsum 2(3, 4) rsum 2(2, 7) rsum 2(1, 9) rsum 2(0, 10) return 10 54

Example: Fibonacci Numbers n Key advantage of tail recursion n Tail-call optimization can save both space and time, because it only needs the address of the tail-call function. int fibo(int n) { if (n == 1 || n == 2) return 1; else return fibo(n - 1) + fibo(n - 2); } int rfibo. Tail(int n, int prev, int cur) { if (n == 1 || n == 2) return cur; else return rfibo. Tail(n - 1, cur, prev + cur); } 55

Example: Finding Maximum Number n How to implement a tail-recursive version int find. Max(int* arr, int n) { int max = arr[0]; for (int i = 1; i < n; i++) if (arr[i] > max) max = arr[i]; return max; } int rfind. Max. Tail(int* arr, int n, int max) { if (n == 1) return max; else { if (max < arr[n - 1]) max = arr[n - 1]; return rfind. Max. Tail(arr, n - 1, max); } } 56