CS 6045 Advanced Algorithms Greedy Algorithms Greedy Algorithms

CS 6045: Advanced Algorithms Greedy Algorithms

Greedy Algorithms • Main Concept – Divide the problem into multiple steps (sub-problems) – For each step take the best choice at the current moment (Local optimal) (Greedy choice) – A greedy algorithm always makes the choice that looks best at the moment – The hope: A locally optimal choice will lead to a globally optimal solution • For some problems, it works. For others, it does not

Greedy Algorithms • A greedy algorithm always makes the choice that looks best at the moment – The hope: a locally optimal choice will lead to a globally optimal solution – For some problems, it works • Dynamic programming can be overkill (slow); greedy algorithms tend to be easier to code – Activity-Selection Problem – Huffman Codes

Activity-Selection Problem • Problem: get your money’s worth out of a carnival – Buy a wristband that lets you onto any ride – Lots of rides, each starting and ending at different times – Your goal: ride as many rides as possible • Another, alternative goal that we don’t solve here: maximize time spent on rides • Welcome to the activity selection problem

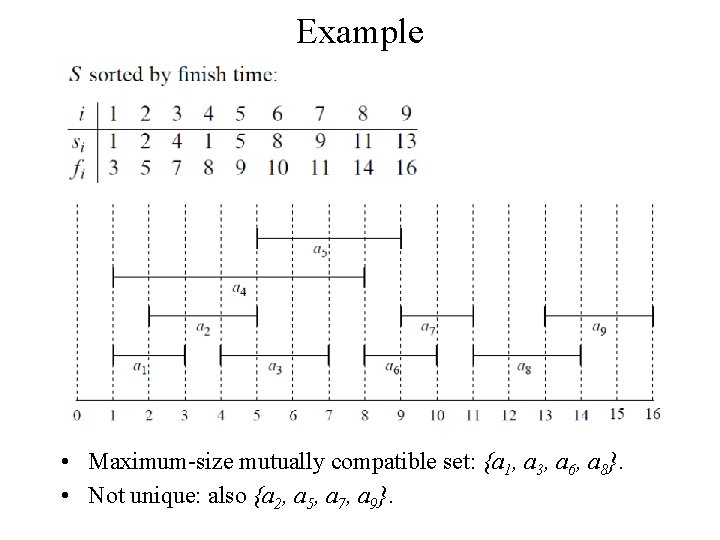
Activity-Selection • Formally: – Given a set S of n activities S = {a 1, …, an} si = start time of activity i fi = finish time of activity i – Find max-size subset A of compatible (non-overlapping ) activities 3 1 n 2 4 6 5 Assume that f 1 f 2 … fn

Example • Maximum-size mutually compatible set: {a 1, a 3, a 6, a 8}. • Not unique: also {a 2, a 5, a 7, a 9}.

Activity Selection: Optimal Substructure •

Activity Selection: Optimal Substructure •

Activity Selection: Dynamic Programming •

Greedy Choice Property • Dynamic programming – Solve all the sub-problems • Activity selection problem also exhibits the greedy choice property: – We should choose an activity that leaves the resource available for as many other activities as possible – The first greedy choice is a 1, since f 1 f 2 … fn

Activity Selection: A Greedy Algorithm • So actual algorithm is simple: – Sort the activities by finish time – Schedule the first activity – Then schedule the next activity in sorted list which starts after previous activity finishes – Repeat until no more activities • Intuition is even more simple: – Always pick the shortest ride available at the time

Activity Selection: A Greedy Algorithm Greedy Choice: Select the next best activity (Local Optimal) • Select the activity that ends first (smallest end time) – Intuition: it leaves the largest possible empty space for more activities • Once selected an activity – Delete all non-compatible activities – They cannot be selected • Repeat the algorithm for the remaining activities – Either using iterations or recursion Sub-problem: We created one sub-problem to solve (Find the optimal schedule after the selected activity) Hopefully when we merge the local optimal + the subproblem optimal solution we get a global optimal

Greedy Algorithm Correctness • Theorem: – If Sk (activities that start after ak finishes) is nonempty and am has the earliest finish time in Sk, then am is included in some optimal solution. • How to prove it? – We can convert any other optimal solution (S’) to the greedy algorithm solution (S) • Idea: – Compare the activities in S’ and S from left-to-right – If they match in the selected activity skip – If they do not match, we can replace the activity in S’ by that in S because the one in S finishes first

Example We mapped S’ to S and • S: {a 1, a 3, a 6, a 8}. showed that S is even better • S’: {a 2, a 5, a 7, a 9}. • a 2, a 5, a 7, a 9 in S’ can be replaced by a 1, a 3, a 6, a 8 from S (finishes earlier)

Recursive Solution Two arrays containing the start and end times (Assumption: they are sorted based on end times) The activity chosen in the last call The problem size Recursive-Activity-Selection(s, f, k, n) m = k +1 Find the next activity starting after While (m <= n) && ( s[m] < f[k]) the end of k m++; If (m <= n) return {Am} U Recursive-Activity-Selection(s, f, m, n) Else return Φ Time Complexity: O(n) (Assuming arrays are already sorted, otherwise we add O(n Log n)

Iterative Solution Two arrays containing the start and end times (Assumption: they are sorted based on end times) Iterative-Activity-Selection(s, f) n = s. length A = {a 1} k = 1 for (m = 2 to n) if (S[m] >= f[k]) A = A U {am} k = m Return A

Elements Of Greedy Algorithms • Greedy-Choice Property – At each step, we do a greedy (local optimal) choice • Top-Down Solution – The greedy choice is usually done independent of the sub-problems – Usually done “before” solving the sub-problem • Optimal Substructure – The global optimal solution can be composed from the local optimal of the sub-problems

Elements Of Greedy Algorithms • Proving a greedy solution is optimal – Remember: Not all problems have optimal greedy solution – If it does, you need to prove it – Usually the proof includes mapping or converting any other optimal solution to the greedy solution

Review: The Knapsack Problem • 0 -1 knapsack problem: – The thief must choose among n items, where the ith item worth vi dollars and weighs wi pounds – Carrying at most W pounds, maximize value • Note: assume vi, wi, and W are all integers • “ 0 -1” b/c each item must be taken or left in entirety • A variation, the fractional knapsack problem: – Thief can take fractions of items – Think of items in 0 -1 problem as gold ingots, in fractional problem as buckets of gold dust

Review: The Knapsack Problem And Optimal Substructure • Both variations exhibit optimal substructure • To show this for the 0 -1 problem, consider the most valuable load weighing at most W pounds – If we remove item j from the load, what do we know about the remaining load? – A: remainder must be the most valuable load weighing at most W - wj that thief could take from museum, excluding item j

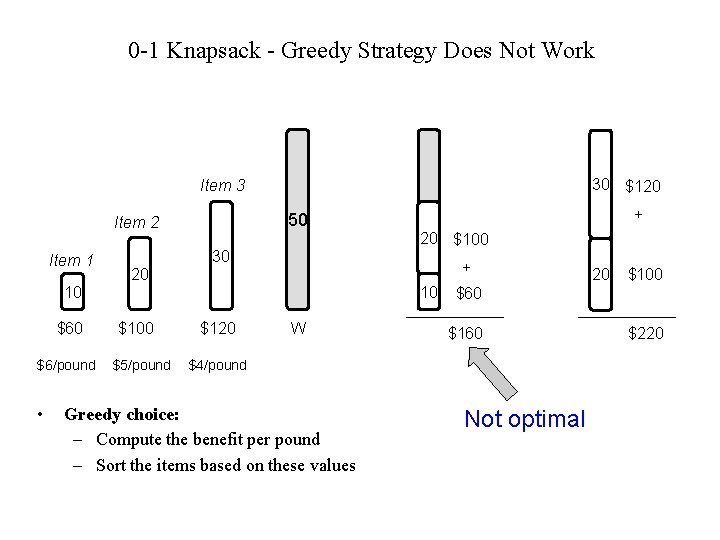
Solving The Knapsack Problem • The optimal solution to the 0 -1 problem cannot be found with the same greedy strategy – Greedy strategy: take in order of dollars/pound – Example: 3 items weighing 10, 20, and 30 pounds, knapsack can hold 50 pounds • Suppose 3 items are worth $60, $100, and $120. • Will greedy strategy work?

0 -1 Knapsack - Greedy Strategy Does Not Work 30 $120 Item 3 50 Item 2 Item 1 30 $6/pound • 20 $100 + 20 10 $60 50 10 $100 $5/pound $120 W 20 + $100 $60 $160 $4/pound Greedy choice: – Compute the benefit per pound – Sort the items based on these values 50 Not optimal $220

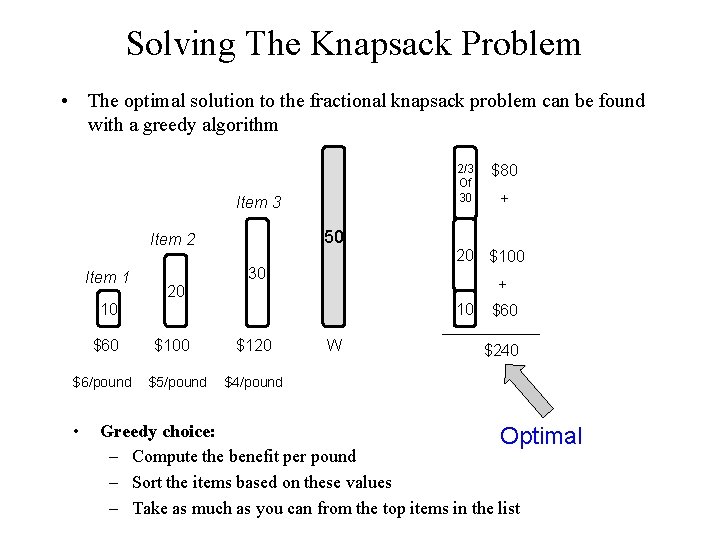
Solving The Knapsack Problem • The optimal solution to the fractional knapsack problem can be found with a greedy algorithm 2/3 Of 30 Item 3 50 Item 2 Item 1 30 $6/pound • 20 $100 + 10 $100 $5/pound $120 + 50 20 10 $60 $80 W $60 $240 $4/pound Greedy choice: Optimal – Compute the benefit per pound – Sort the items based on these values – Take as much as you can from the top items in the list

The Knapsack Problem: Greedy Vs. Dynamic • The fractional problem can be solved greedily • The 0 -1 problem cannot be solved with a greedy approach – As you have seen, however, it can be solved with dynamic programming

Huffman code • Computer Data Encoding: – How do we represent data in binary? • Historical Solution: – Fixed length codes – Encode every symbol by a unique binary string of a fixed length. – Examples: ASCII (7 bit code), – EBCDIC (8 bit code), …

American Standard Code for Information Interchange

ASCII Example: AABCAA A A B C A A 1000001 1000010 1000011 1000001

Total space usage in bits: Assume an ℓ bit fixed length code. For a file of n characters Need nℓ bits.

Variable Length codes • Idea: In order to save space, use less bits for frequent characters and more bits for rare characters. • Example: suppose alphabet of 3 symbols: { A, B, C }. suppose in file: 1, 000 characters. • Need 2 bits for a fixed length code for a total of 2, 000 bits.

Variable Length codes - example Suppose the frequency distribution of the characters is: Encode: A B C 999, 000 500 A 0 B 10 C 11 Note that the code of A is of length 1, and the codes for B and C are of length 2

Total space usage in bits: Fixed code: 1, 000 x 2 = 2, 000 Variable code: 999, 000 x 1 + 500 x 2 1, 000 A savings of almost 50%

How do we decode? In the fixed length, we know where every character starts, since they all have the same number of bits. Example: A = 00 B = 01 C = 10 00000001011010100100001010 A A A BB C CC B A A CC

How do we decode? In the variable length code, we use an idea called Prefix code, where no code is a prefix of another. Example: A = 0 B = 10 C = 11 None of the above codes is a prefix of another.

How do we decode? Example: A = 0 B = 10 C = 11 So, for the string: AAABBC C CBC BAACC 0 0 0101011111110 0 01111 the encoding:

Prefix Code Example: A = 0 B = 10 C = 11 Decode the string 0 0 0101011111110 0 01111 A A A B B C C C B A AC C

Desiderata: Construct a variable length code for a given file with the following properties: 1. Prefix code. 2. Using shortest possible codes. 3. Efficient.

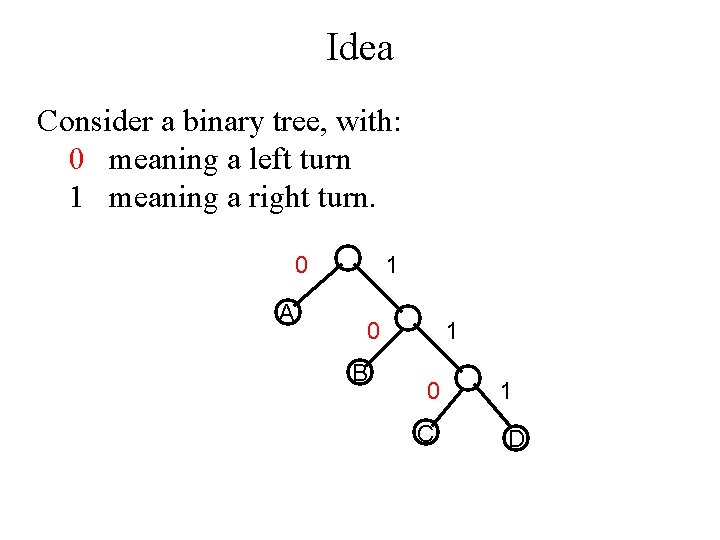
Idea Consider a binary tree, with: 0 meaning a left turn 1 meaning a right turn. 0 A 1 0 B 1 0 C 1 D

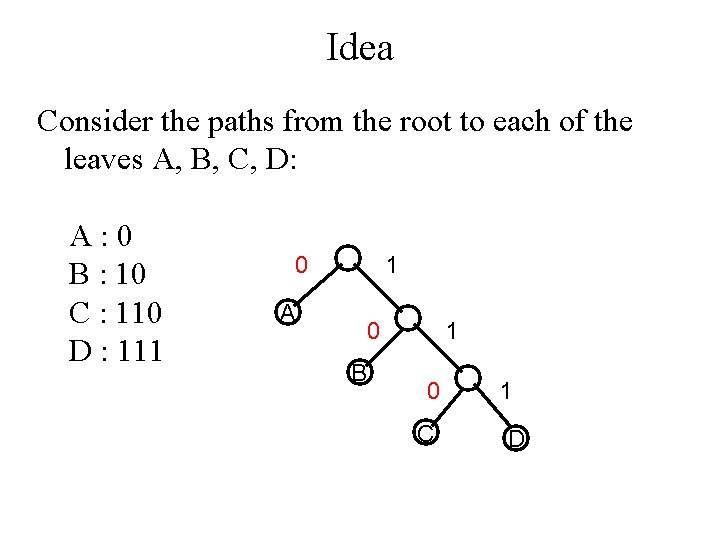
Idea Consider the paths from the root to each of the leaves A, B, C, D: A: 0 B : 10 C : 110 D : 111 0 1 A 0 B 1 0 C 1 D

Observe: 1. This is a prefix code, since each of the leaves has a path ending in it, without continuation. 2. If the tree is full then we are not “wasting” bits. 3. If we make sure that the more frequent symbols are closer to the root then they will have a smaller code. 0 1 A 0 B 1 0 C 1 D

Greedy Algorithm: 1. Consider all pairs: <frequency, symbol>. 2. Choose the two lowest frequencies, and make them brothers, with the root having the combined frequency. 3. Iterate.

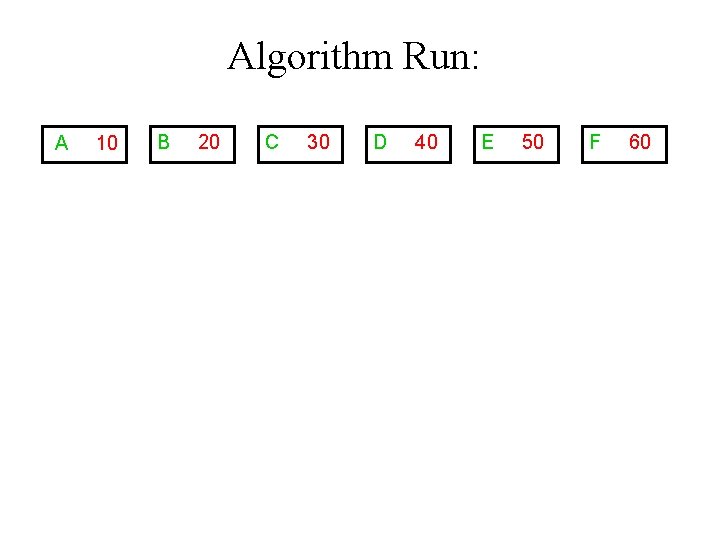
Greedy Algorithm Example: Alphabet: A, B, C, D, E, F Frequency table: A B C D E F 10 20 30 40 50 60 Total File Length: 210

Algorithm Run: A 10 B 20 C 30 D 40 E 50 F 60

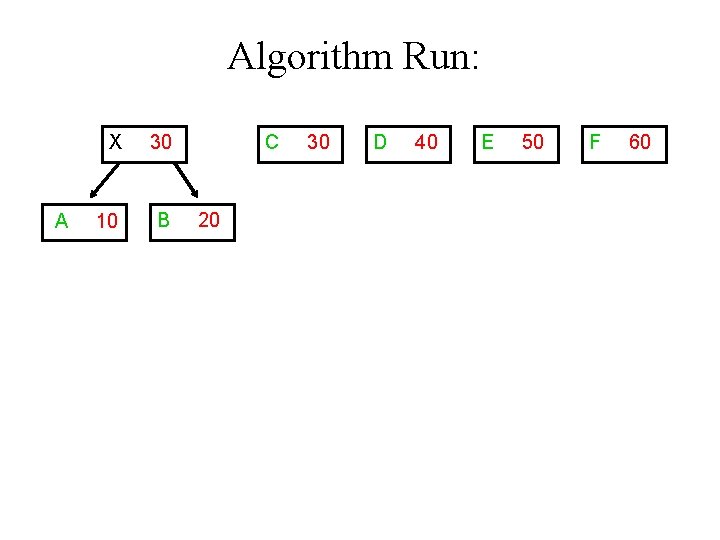
Algorithm Run: A X 30 10 B C 20 30 D 40 E 50 F 60

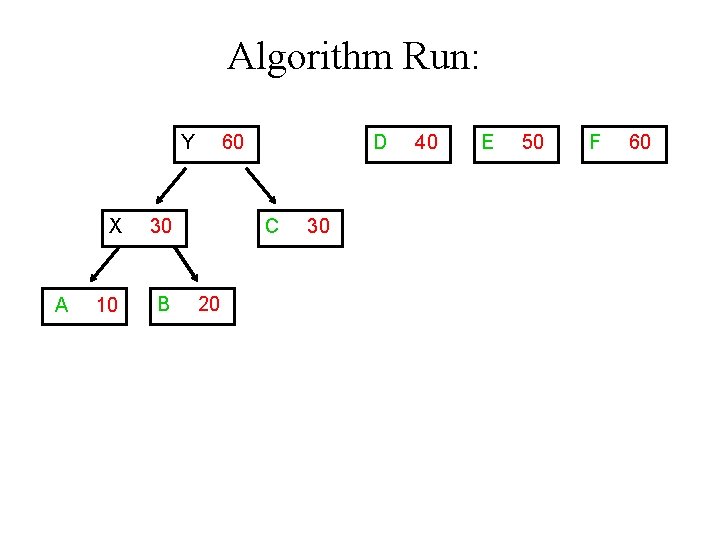
Algorithm Run: Y A X 30 10 B 60 D C 20 30 40 E 50 F 60

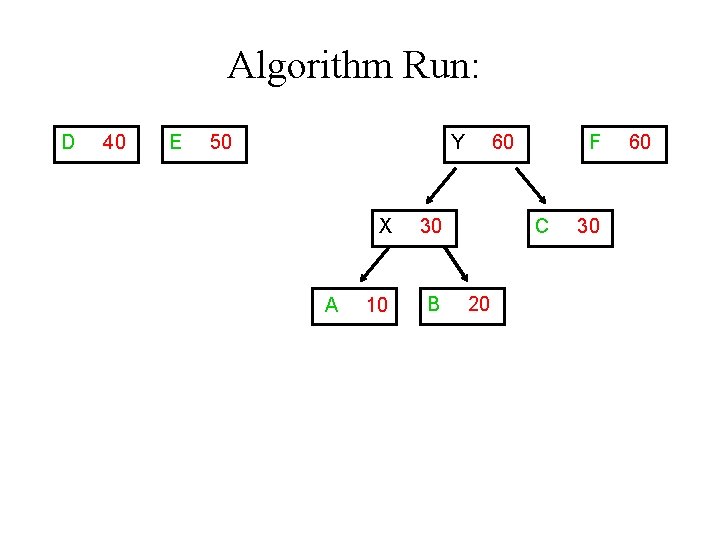
Algorithm Run: D 40 E 50 Y A X 30 10 B 60 F C 20 30 60

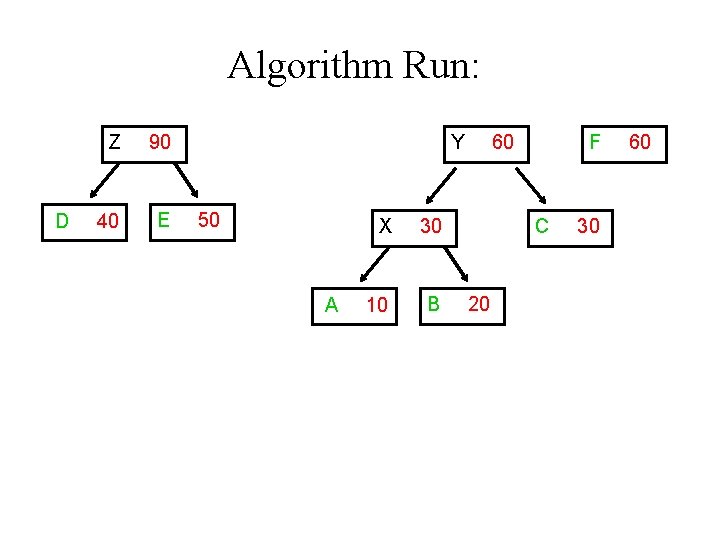
Algorithm Run: D Z 90 40 E Y 50 A X 30 10 B 60 F C 20 30 60

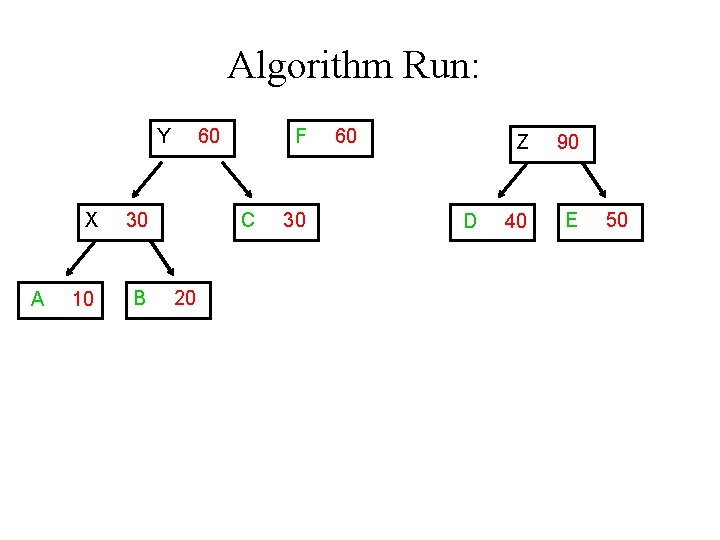
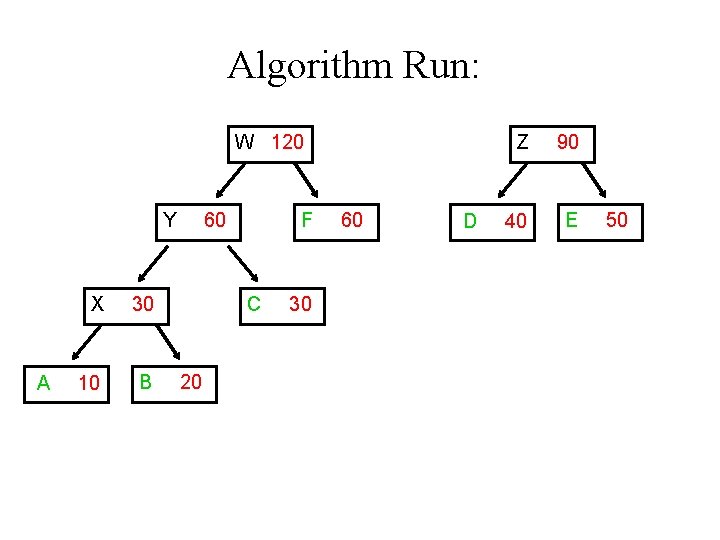
Algorithm Run: Y A X 30 10 B 60 F C 20 30 60 D Z 90 40 E 50

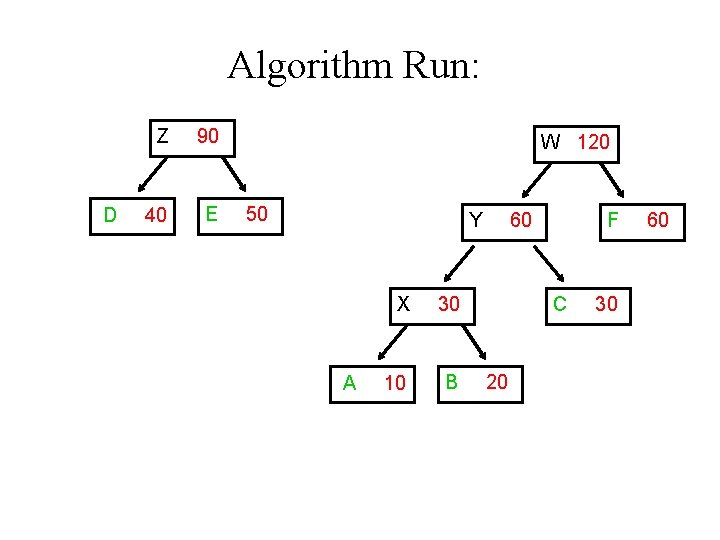
Algorithm Run: W 120 Y A X 30 10 B 60 F C 20 30 60 D Z 90 40 E 50

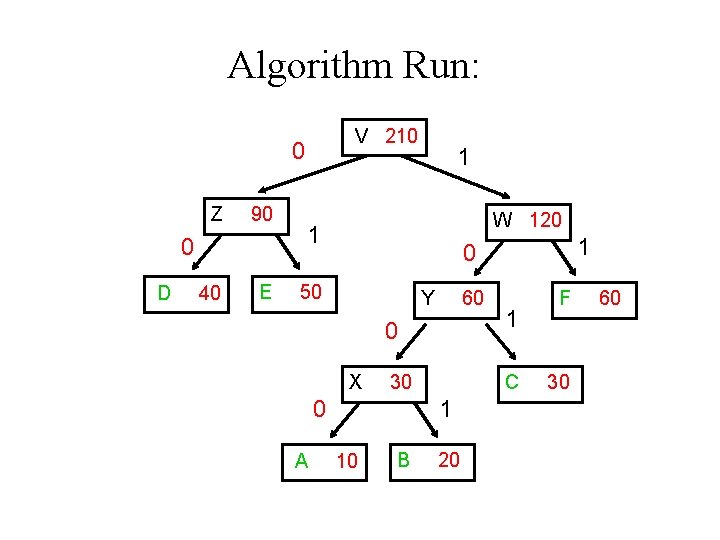
Algorithm Run: D Z 90 40 E W 120 50 Y A X 30 10 B 60 F C 20 30 60

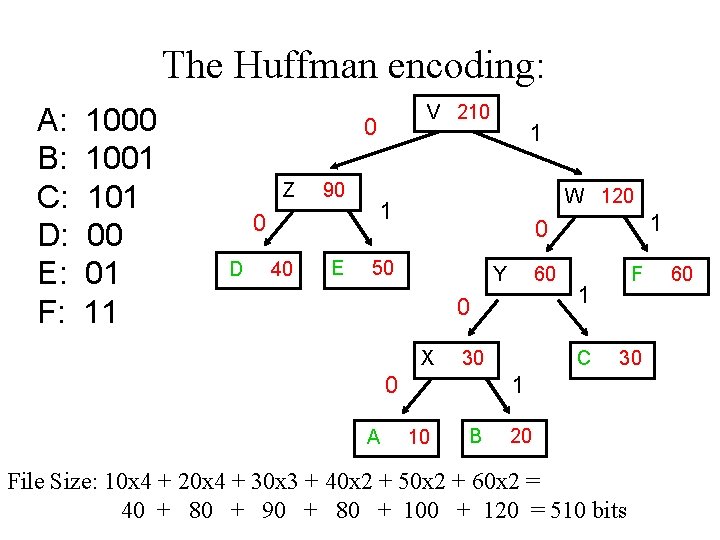
Algorithm Run: V 210 0 Z 90 0 D 40 E 1 W 120 1 50 Y 60 0 X 30 0 A 1 0 C 1 10 B 1 20 F 30 60

The Huffman encoding: A: B: C: D: E: F: 1000 1001 101 00 01 11 V 210 0 Z 90 0 D 40 E 1 W 120 1 50 Y 60 0 X 30 0 A 1 0 F 1 C 30 1 10 B 20 File Size: 10 x 4 + 20 x 4 + 30 x 3 + 40 x 2 + 50 x 2 + 60 x 2 = 40 + 80 + 90 + 80 + 100 + 120 = 510 bits 60

Note the savings: • The Huffman code: • Required 510 bits for the file. • Fixed length code: • Need 3 bits for 6 characters. • File has 210 characters. • Total: 630 bits for the file.

Greedy Algorithm • Initialize trees of a single node each. • Keep the roots of all subtrees in a priority queue. • Iterate until only one tree left: • Merge the two smallest frequency subtrees into a single subtree with two children, and insert into priority queue.

Huffman Algorithm Total run time: (n lgn) Huffman(C) 1. n = |C| 2. Q = C // Q is a binary Min-Heap; (n) Build-Heap 3. for i = 1 to n-1 4. z = Allocate-Node() 5. x = Extract-Min(Q) // (lgn), (n) times 6. y = Extract-Min(Q) // (lgn), (n) times 7. left(z) = x 8. right(z) = y 9. f(z) = f(x) + f(y) 10. Insert(Q, z) // (lgn), (n) times 11. return Extract-Min(Q) // return the root of the tree

Algorithm correctness: Need to prove two things for greedy algorithms: Greedy Choice Property: The choice of local optimum is indeed part of a global optimum. Optimal Substructure Property: When we recursive on the remaining and combine it with the local optimum of the greedy choice, we get a global optimum.

Huffman Algorithm correctness: Greedy Choice Property: There exists a minimum cost prefix tree where the two smallest frequency characters are indeed siblings with the longest path from root. This means that the greedy choice does not hurt finding the optimum.

Algorithm correctness: Optimal Substructure Property: An optimal solution to the problem once we choose the two least frequent elements and combine them to produce a smaller problem, is indeed a solution to the problem when the two elements are added.

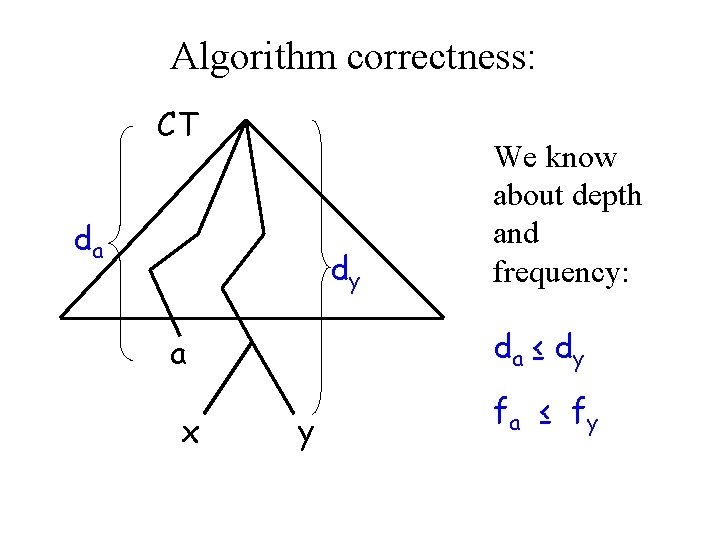
Algorithm correctness: • Greedy Choice Property: • There exists a minimum cost tree where the minimum frequency elements are longest path siblings: • Proof by contradiction: • Assume that is not the situation. Then there are two elements in the longest path. • Say a, b are the elements with smallest frequency and x, y the elements in the longest path

Algorithm correctness: CT da dy da ≤ d y a x We know about depth and frequency: y fa ≤ f y

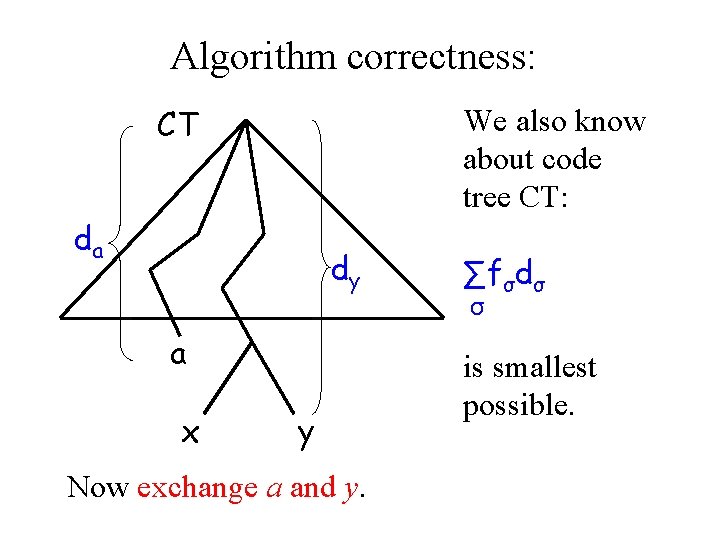
Algorithm correctness: CT We also know about code tree CT: da dy a x y Now exchange a and y. ∑fσdσ σ is smallest possible.

Algorithm correctness: Cost(CT) = ∑fσdσ = CT’ σ ∑fσdσ+fada+fydy≥ da dy σ≠a, y y x a (da ≤ dy, fa ≤ fy Therefore fada ≥fyda and fydy ≥fady ) ∑fσdσ+fyda+fady= σ≠a, y cost(CT’)

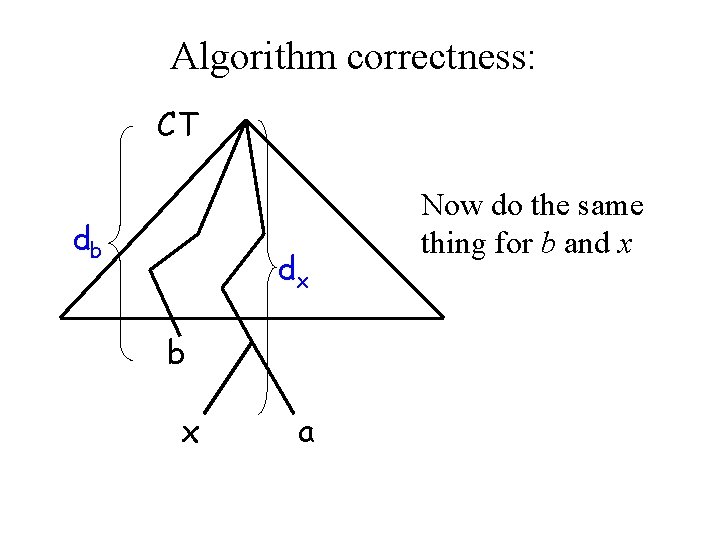
Algorithm correctness: CT db dx b x a Now do the same thing for b and x

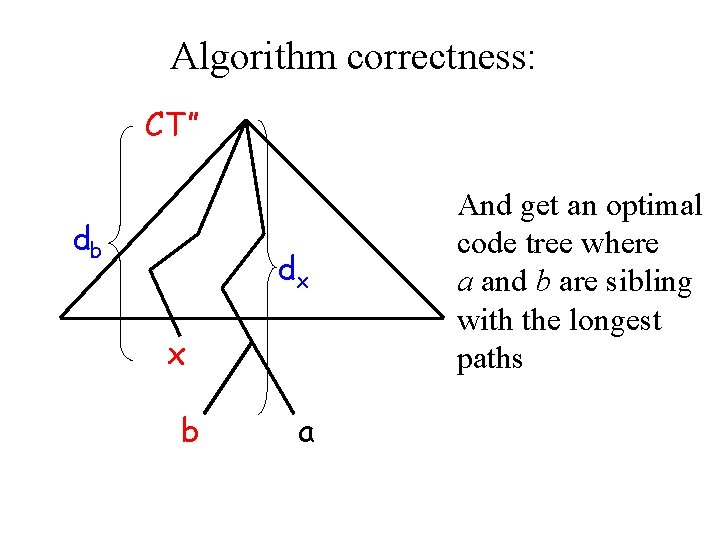
Algorithm correctness: CT” db dx x b a And get an optimal code tree where a and b are sibling with the longest paths

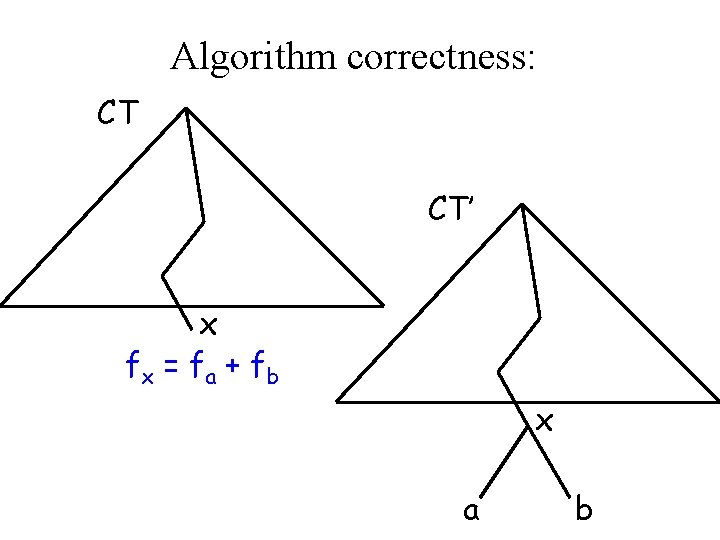
Algorithm correctness: Optimal substructure property: Let a, b be the symbols with the smallest frequency. Let x be a new symbol whose frequency is fx =fa +fb. Delete characters a and b, and find the optimal code tree CT for the reduced alphabet. Then CT’ = CT U {a, b} is an optimal tree for the original alphabet.

Algorithm correctness: CT CT’ x fx = f a + f b x a b

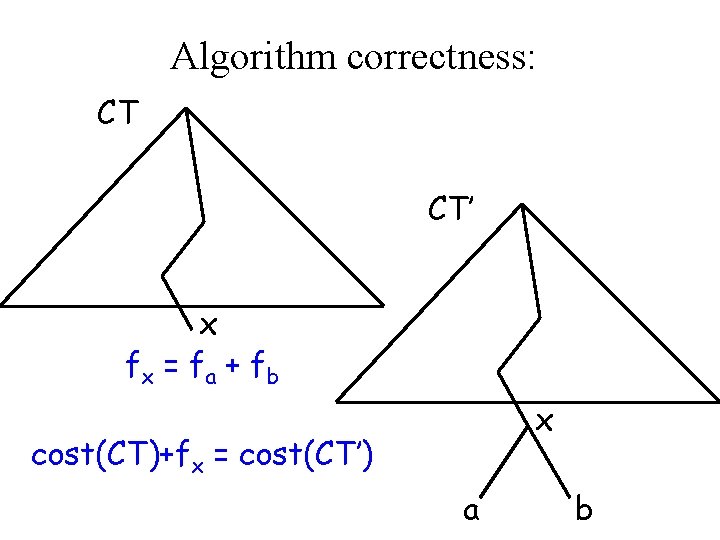
Algorithm correctness: cost(CT’)=∑fσd’σ = ∑fσd’σ + fad’a + fbd’b= σ σ≠a, b ∑fσd’σ + fa(dx+1) + fb (dx+1) = σ≠a, b ∑fσd’σ+(fa + fb)(dx+1)= σ≠a, b ∑fσdσ+fx(dx+1)+fx = cost(CT) + fx σ≠a, b

Algorithm correctness: CT CT’ x fx = f a + f b x cost(CT)+fx = cost(CT’) a b

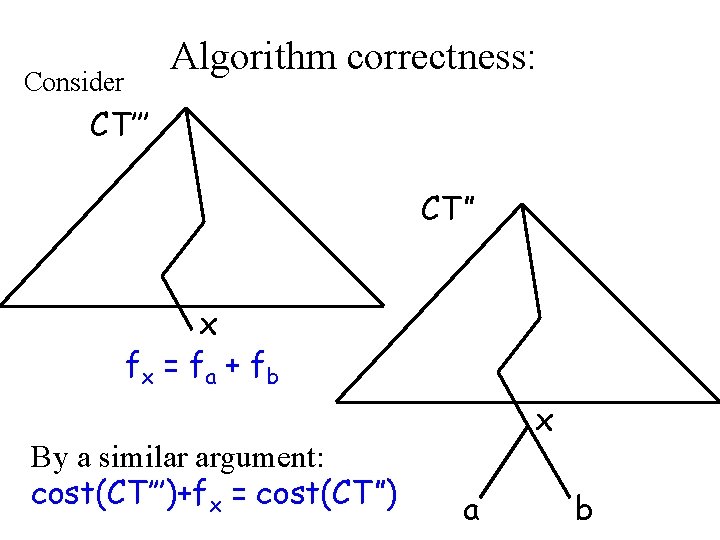
Algorithm correctness: Assume CT’ is not optimal. By the previous lemma there is a tree CT” that is optimal, and where a and b are siblings. So cost(CT”) < cost(CT’)

Consider Algorithm correctness: CT’’’ CT” x fx = f a + f b By a similar argument: cost(CT’’’)+fx = cost(CT”) x a b

Algorithm correctness: We get: cost(CT’’’) = cost(CT”) – fx < cost(CT’) – fx = cost(CT) and this contradicts the minimality of cost(CT).

Greedy Vs. Dynamic • Greedy Algorithms – Can assemble a globally optimal solution by making locally optimal choices – Making the choice before solving the sub-problems – Top-down (simpler and more efficient) – Can solve some problems optimally • Dynamic Programming – Choice depends on knowing optimal solutions to subproblems. Solve all sub-problems – Bottom-up (slow) – Can solve more problems optimally