ALGORITHMS Heuristic algorithms method of sorting HEURISTIC ALGORITHMS

ALGORITHMS Heuristic algorithms & method of sorting

HEURISTIC ALGORITHMS o Heuristic algorithm is a method of problem solving using exploration, trial and error methods o May not lead to the best or optimal solution of the problem

Heuristic algorithms for Bin-Packing o People move belongings need efficient packing o With odd sizes belongings, hard to formulate algorithm for packing efficiently o Also arises in copying computer files of varying sizes to diskettes o What is the fewest number of diskettes required? o It depends on how efficient the memory space in each diskette is fully utilised

Heuristic algorithms o First-fit Algorithm o First-fit decreasing Algorithm o Full bins

First-fit Algorithm o Also sometimes called greedy algorithm. o Provides a fast but often non-optimal solution o Taking the boxes in the order listed, place the next box to be packed in the first available slot that can take the box in the bin

First-fit Algorithm o Each box is selected and attempts made to place it in the first bin. o If this fails then the second bin is tried. o If this fails the next bin is tried and so on until eventually the element is placed into a bin. o The result is not necessarily optimal.

First-fit Decreasing Algorithm o The simplest heuristic algorithms for solving the bin packing problem. o Operates by first sorting the items to be inserted in decreasing order by volume, inserting each item into the first bin in the list with sufficient remaining space. o First sorting the list of elements into decreasing order, does not guarantee an optimal solution, and, particularly for longer list, can increase the time taken to implement the algorithm.

Full bins Algorithms o Look for combinations of boxes to fill bins. o Pack these boxes. o For the remainder, place the next box to be packed in the first available slot that can take that box o Required a lot of different combinations of boxes to be checked if they make full bins

EXAMPLE 1 o Eleven boxes to be packed into crates o Each crate must weight not more than 100 kg. There are three boxes of weight 50 kg, three of weight 40 kg, three of weight 30 kg and two of weight 20 kg. o 1) Apply first fit decreasing algorithms and state number of crates used o 2) Apply full-bin algorithm and state the number of crates used

Applying First fit Decreasing Algorithms o Rearrange the boxes in decreasing size 50 50 50 40 40 40 30 30 30 20 20

Applying First fit Decreasing Algorithms o Stack the boxes in decreasing weight into crates on condition no crates exceed 100 kg 30 50 40 40 30 20 50 50 40 30 20 Crate 1 Crate 2 Crate 3 Crate 4 5 crates required Crate 5

Applying Full-Bin Algorithms o Stack the boxes in decreasing weight into crates on condition no crates exceed 100 kg 20 20 30 50 30 40 30 50 50 40 40 Crate 1 Crate 2 Crate 3 Crate 4 4 crates required

EXERCISE o There are 11 boxes, A to K with heights (in cm) as follows A B C D E F G H I J K 8 7 4 9 6 9 5 5 6 7 8 o The rack is 15 cm high and you are asked to stack boxes one on top of the other using few slots as possible o State all the steps that you take.

SORTING ALGORITHMS o Algorithm that put elements of a list in a certain order o The most used orders are numerical order and lexicographical order o Efficient sorting is important to optimize the use of other algorithm

Methods of sorting o Interchange sort o Bubble sort o Shuttle sort o Quick sort

Interchange Sort o Any sorting algorithm that is based on swapping. o In this algorithm, the smallest number in the list is found and interchanged with the first number. o Then the smallest number excluding the first is found and interchanged with the second number. o This process continues until the list is sorted.

EXAMPLE 1 (Interchange sort) 7 5 2 4 1 5 1 2 2 5 4 4 10 1 6 3 10 10 7 7 6 6 3 3 Original list 1 st pass 2 nd pass 1 2 3 4 1 2 10 7 6 5 5 7 6 10 5 6 3 rd pass 4 th pass 5 th pass 3 4 7 10 6 th pass 1 2 3 4 5 6 7 10 7 th pass

EXAMPLE 1 (Interchange sort) 7 5 2 4 1 5 1 2 2 5 4 4 10 1 6 3 10 10 7 7 6 6 3 3 Original list 1 st pass 2 nd pass 1 2 3 4 1 2 10 7 6 5 5 7 6 10 5 6 3 rd pass 4 th pass 5 th pass 3 4 7 10 6 th pass 1 2 3 4 5 6 7 10 7 th pass

Bubble Sort The algorithm gets its name from the way smaller elements "bubble" to the top (i. e. the beginning) of the list via the swaps. n Because it only uses comparisons to operate on elements, it is a comparison sort. n Although simple, this algorithm is highly inefficient and is rarely used except in education. n

Bubble Sort n n n A straightforward and simplistic method of sorting data that is used in computer science education. The algorithm starts at the beginning of data set. It compares the first two elements, and if the first is greater than the second, it swaps them. Continues for each pair of adjacent elements to the end of data set. Starts again with first two elements, repeating until no swaps have occurred on the last pass.

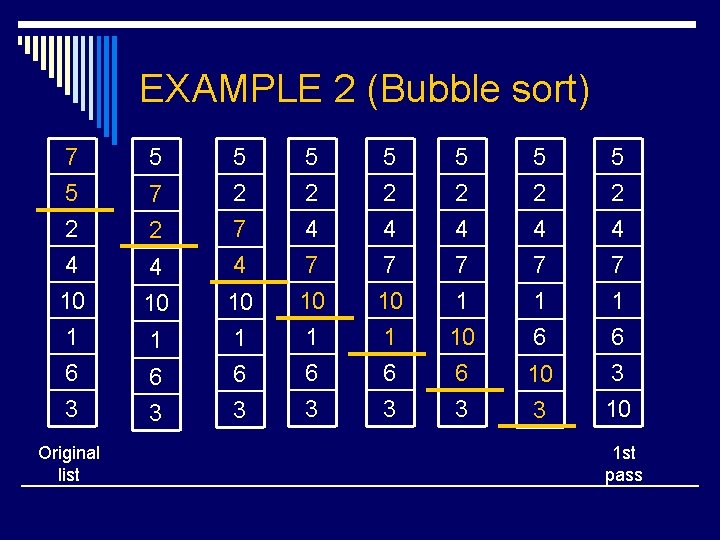
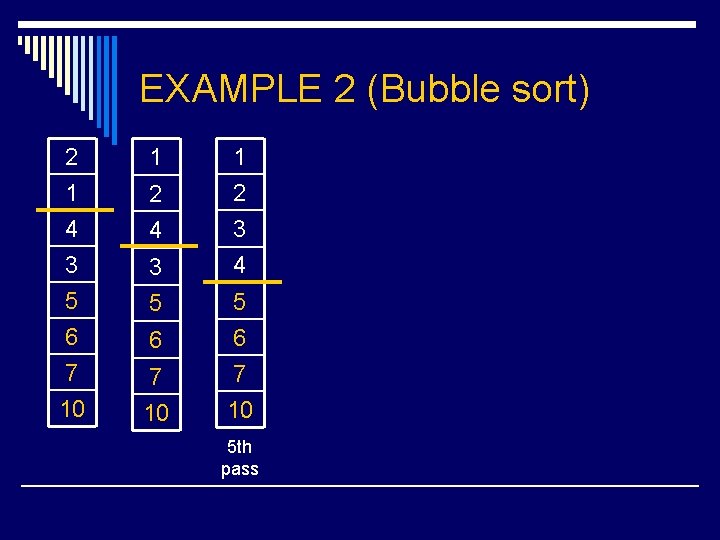
EXAMPLE 2 (Bubble sort) 7 5 2 4 5 10 1 6 3 Original list 7 5 2 2 7 4 4 10 10 1 1 6 6 3 3 5 2 4 7 5 2 10 1 6 3 1 10 6 3 1 6 4 7 10 3 5 2 4 7 1 6 3 10 1 st pass

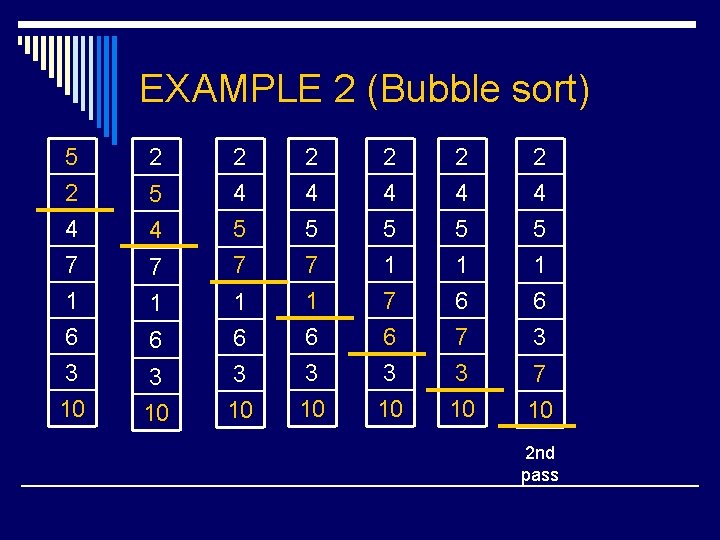
EXAMPLE 2 (Bubble sort) 5 2 4 7 2 5 2 4 4 5 7 7 1 6 3 10 1 1 6 6 3 3 10 10 2 4 5 7 2 4 5 1 2 4 1 6 3 10 7 6 3 10 6 7 3 10 6 3 5 1 7 10 2 nd pass

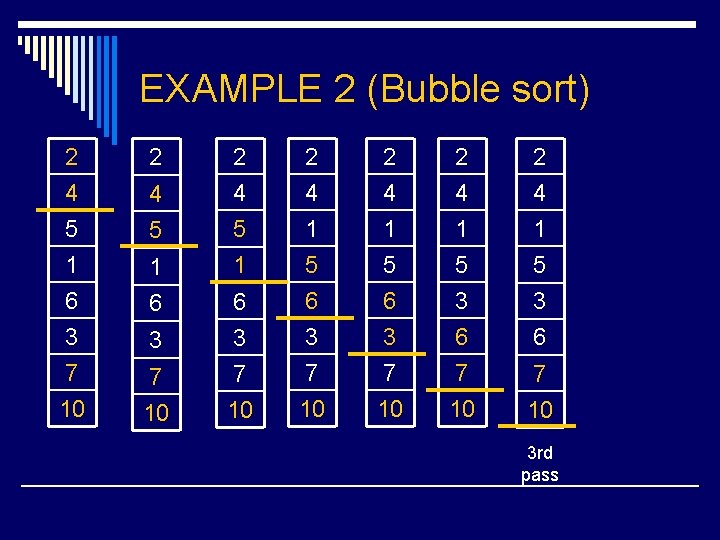
EXAMPLE 2 (Bubble sort) 2 4 5 1 2 4 5 5 1 1 6 3 7 10 6 6 3 3 7 7 10 10 2 4 1 5 2 4 6 3 7 10 3 6 1 5 7 10 3 rd pass

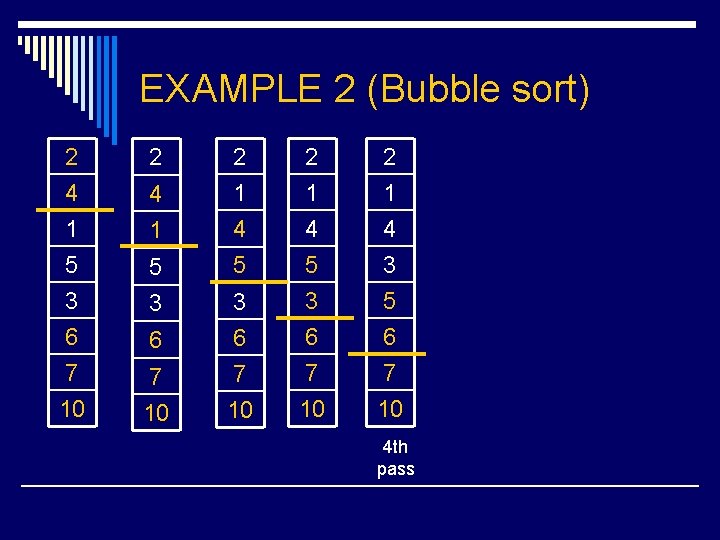
EXAMPLE 2 (Bubble sort) 2 4 1 5 2 4 2 1 1 4 5 5 3 6 7 10 3 3 6 6 7 7 10 10 2 1 4 5 2 1 4 3 3 6 7 10 5 6 7 10 4 th pass

EXAMPLE 2 (Bubble sort) 2 1 4 3 1 2 4 3 3 4 5 6 7 10 5 5 6 6 7 7 10 10 5 th pass

Shuttle Sort o Repeatedly taking the next item and inserting it into the final data structure in its proper order with respect to items already inserted. o Known as insertion sort. o First, the first two numbers are compared and swap if necessary to place in ascending order. o Process is continued until numbers are in the ascending order.

Shuttle Sort 1 st pass: o Compare first and second number in the list. Swap if necessary to place the number in ascending order. 2 nd pass: o Compare 2 nd and 3 rd number and swap if necessary. Then compare 1 st and 2 nd and swap if necessary 3 rd pass: o Compare 3 rd and 4 th number and swap if necessary. Compare 2 nd and 3 rd number and swap if necessary. Then compare 1 st and 2 nd and swap if necessary

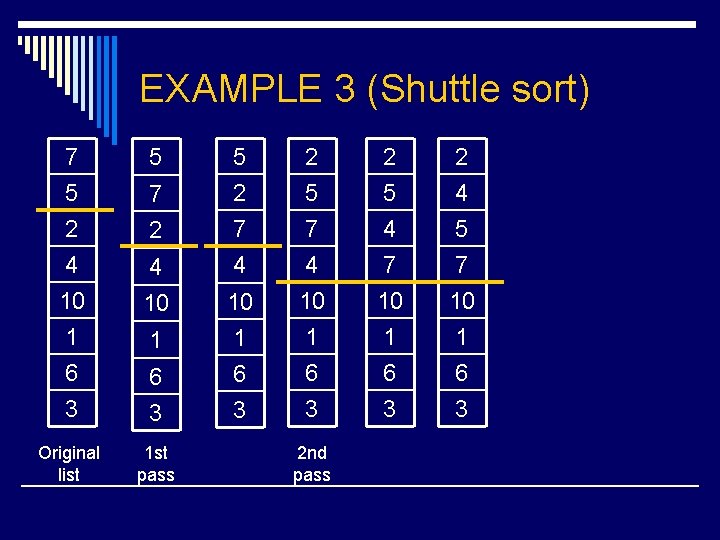
EXAMPLE 3 (Shuttle sort) 7 5 2 4 5 7 5 2 2 7 4 4 10 1 6 3 10 10 1 1 6 6 3 3 Original list 1 st pass 2 5 7 4 2 5 4 7 2 4 5 7 10 1 6 3 2 nd pass

EXAMPLE 3 (Shuttle sort) 2 4 5 7 2 4 5 5 7 7 10 1 6 3 10 1 1 10 6 6 3 3 3 rd pass 4 th pass 2 4 5 1 2 4 1 5 2 1 4 5 1 2 4 5 7 10 6 3

EXAMPLE 3 (Shuttle sort) 1 2 4 5 1 2 7 10 6 3 7 6 10 3 6 5 th pass 4 5 7 10 3 1 2 4 5 1 2 4 3 1 2 3 4 6 7 3 10 6 3 7 10 3 6 7 10 5 6 7 10 6 th pass 7 th pass

Quick Sort o A well-known sorting algorithm developed by C. A. R. Hoare. o A comparison sort. o Sorts by employing a divide and conquer strategy to divide a list into two sub-lists. o Pick an element, called a pivot, from the list.

Quick Sort o First split the list into two sub-lists: (1) Number less than or equal to first number in the list (2)Number greater than the first number in the list o Place the first number between the two sublists o Repeat the process on sub-lists containing two or more numbers until there are no sublists

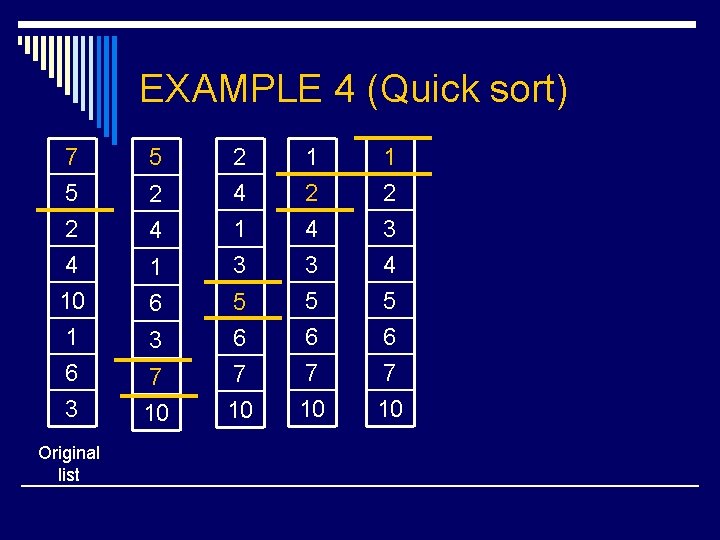
EXAMPLE 4 (Quick sort) 7 5 2 4 5 10 1 6 3 Original list 2 2 4 4 1 1 3 6 5 3 6 7 7 10 10 1 2 4 3 1 2 3 4 5 6 7 10