Analysis of Algorithms Asymptotic Performance Review Asymptotic Performance






































![Analysis of Insertion Sort INSERTION-SORT(A) cost times 1. for j = 2 to length[A] Analysis of Insertion Sort INSERTION-SORT(A) cost times 1. for j = 2 to length[A]](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-42.jpg)




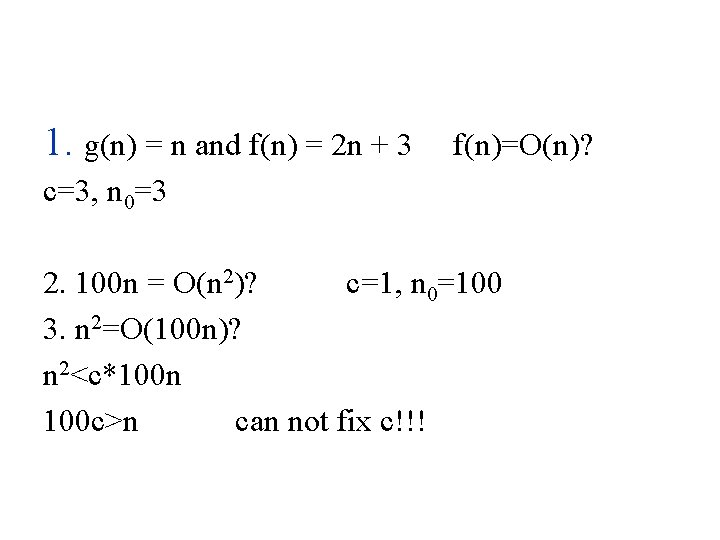
![Linear search // Searches an unordered array of integers int search(int data[], int n, Linear search // Searches an unordered array of integers int search(int data[], int n,](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-48.jpg)
![Bubble sort void bubble. Sort ( int A[] , int n ) { for Bubble sort void bubble. Sort ( int A[] , int n ) { for](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-49.jpg)

![Non recursive int bin. Search ( int A[] , int n , int x Non recursive int bin. Search ( int A[] , int n , int x](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-58.jpg)

![Recursive int binary(int a[], int n, int m, int l, int u){ int mid, Recursive int binary(int a[], int n, int m, int l, int u){ int mid,](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-60.jpg)






![Merge Sort: Sorting an array recursively void mergesort (int A[], int n) { int Merge Sort: Sorting an array recursively void mergesort (int A[], int n) { int](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-70.jpg)

- Slides: 71

Analysis of Algorithms Asymptotic Performance

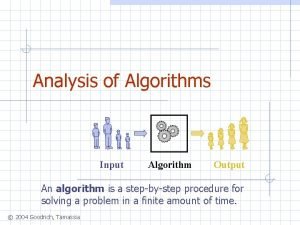
Review: Asymptotic Performance • Asymptotic performance: How does algorithm behave as the problem size gets very large? o Running time o Memory/storage requirements § Remember that we use the Hypothetical machine (Random Access Machine): o All memory equally expensive to access o No concurrent operations o All reasonable instructions take unit time (ci)

Review: Running Time • Number of primitive steps that are executed § Except for time of executing a function call most statements roughly require the same amount of time § We can be more exact if need be

Example int a, b, larger; scanf(“%d %d”, &a, &b); larger = b; if (a > b) larger = a; printf(“Larger number is %dn”, larger); Running time T=c 1+c 2+c 3+c 4+c 5+c 6=C (constant) c 1 c 2 c 3 c 4 c 5 c 6

Sum of first N natural numbers void main() { int N, count, sum; scanf (“%d”, &N) ; sum = 0; count = 1; while (count <= N) { sum = sum + count; count = count + 1; } printf (“Sum = %dn”, sum) ; } T(n)=c 1+c 2+c 3+c 4+c 5+c 6*(n+1)+c 7*n+c 8*n+c 9 =C’+c 6*(n+1)+c 7*n+c 8*n c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9

2 -D Figure: with for loop Print. . * * * for (row=1; row<=n; ++row) { (n+1) for (col=1; col<=n; ++col) { n*(n+1) * * * printf(“* ”); n*n * * * } printf(“n”); } n

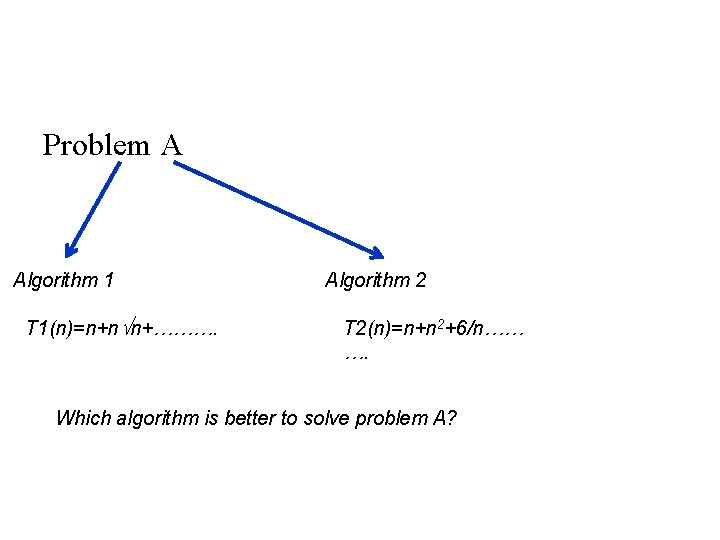
Problem A Algorithm 1 T 1(n)=n+n n+………. Algorithm 2 T 2(n)=n+n 2+6/n…… …. Which algorithm is better to solve problem A?

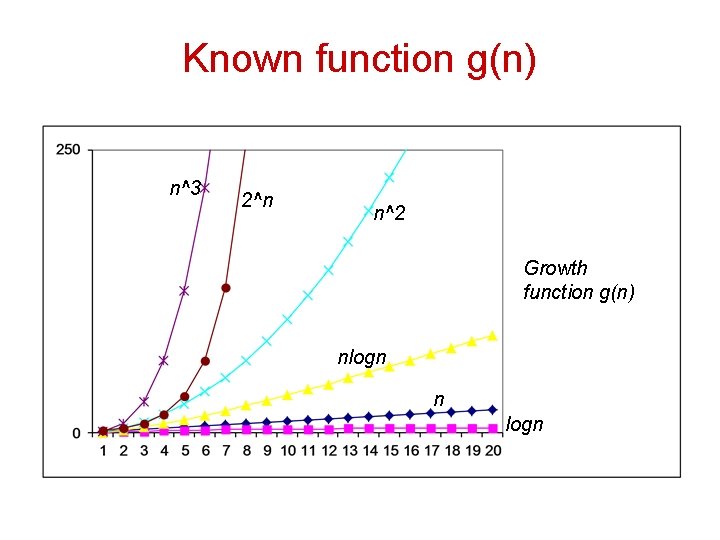
T(n)=> unknown function Map this to a known function g(n) Behavior of g(n) is known to us

Known function g(n) n^3 2^n n^2 Growth function g(n) nlogn n logn

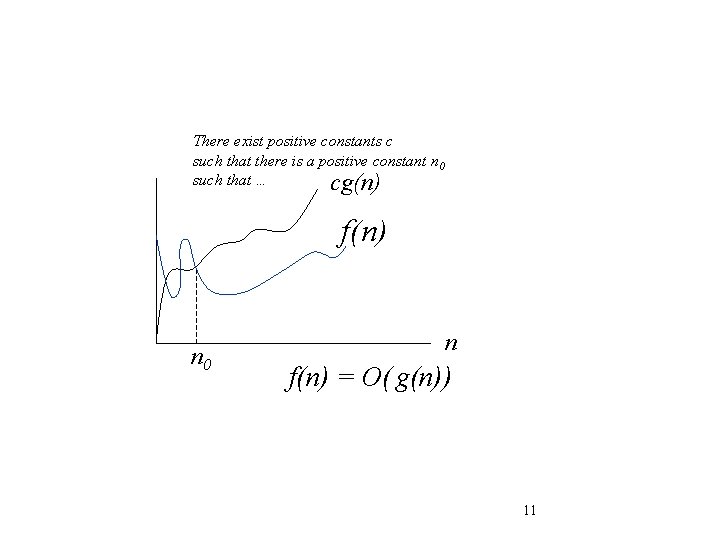
Upper Bound Notation Read O as “Big-O” (you’ll also hear it as “order”) • • In general a function § f(n) is O(g(n)) if there exist positive constants c and n 0 such that f(n) c g(n) for all n n 0 Formally § O(g(n)) = { f(n): positive constants c and n 0 such that f(n) c g(n) n n 0

There exist positive constants c such that there is a positive constant n 0 such that … cg(n) f(n) n 0 n f(n) = O( g(n)) 11

An Example: Insertion Sort Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 30 10 40 20 1 2 3 4 i = j = key = A[j] = A[j+1] = Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 30 10 40 20 1 2 3 4 i = 2 j = 1 A[j] = 30 key = 10 A[j+1] = 10 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 30 30 40 20 1 2 3 4 i = 2 j = 1 A[j] = 30 key = 10 A[j+1] = 30 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 30 30 40 20 1 2 3 4 i = 2 j = 1 A[j] = 30 key = 10 A[j+1] = 30 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 30 30 40 20 1 2 3 4 i = 2 j = 0 A[j] = key = 10 A[j+1] = 30 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 30 30 40 20 1 2 3 4 i = 2 j = 0 A[j] = key = 10 A[j+1] = 30 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 2 j = 0 A[j] = key = 10 A[j+1] = 10 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } } David Luebke 19 3/1/2021

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 3 j = 0 A[j] = key = 10 A[j+1] = 10 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 3 j = 0 A[j] = key = 40 A[j+1] = 10 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 3 j = 0 A[j] = key = 40 A[j+1] = 10 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 3 j = 2 A[j] = 30 key = 40 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 3 j = 2 A[j] = 30 key = 40 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 3 j = 2 A[j] = 30 key = 40 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 4 j = 2 A[j] = 30 key = 40 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 4 j = 2 A[j] = 30 key = 20 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 4 j = 2 A[j] = 30 key = 20 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } } David Luebke 28 3/1/2021

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 4 j = 3 A[j] = 40 key = 20 A[j+1] = 20 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 20 1 2 3 4 i = 4 j = 3 A[j] = 40 key = 20 A[j+1] = 20 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 40 1 2 3 4 i = 4 j = 3 A[j] = 40 key = 20 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 40 1 2 3 4 i = 4 j = 3 A[j] = 40 key = 20 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 40 1 2 3 4 i = 4 j = 3 A[j] = 40 key = 20 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 40 1 2 3 4 i = 4 j = 2 A[j] = 30 key = 20 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 40 40 1 2 3 4 i = 4 j = 2 A[j] = 30 key = 20 A[j+1] = 40 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 30 40 1 2 3 4 i = 4 j = 2 A[j] = 30 key = 20 A[j+1] = 30 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 30 40 1 2 3 4 i = 4 j = 2 A[j] = 30 key = 20 A[j+1] = 30 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 30 40 1 2 3 4 i = 4 j = 1 A[j] = 10 key = 20 A[j+1] = 30 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 30 30 40 1 2 3 4 i = 4 j = 1 A[j] = 10 key = 20 A[j+1] = 30 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 20 30 40 1 2 3 4 i = 4 j = 1 A[j] = 10 key = 20 A[j+1] = 20 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } }

An Example: Insertion Sort 10 20 30 40 1 2 3 4 i = 4 j = 1 A[j] = 10 key = 20 A[j+1] = 20 Insertion. Sort(A, n) { for i = 2 to n { key = A[i] j = i - 1; while (j > 0) and (A[j] > key) { A[j+1] = A[j] j = j - 1 } A[j+1] = key } } Done!
![Analysis of Insertion Sort INSERTIONSORTA cost times 1 for j 2 to lengthA Analysis of Insertion Sort INSERTION-SORT(A) cost times 1. for j = 2 to length[A]](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-42.jpg)
Analysis of Insertion Sort INSERTION-SORT(A) cost times 1. for j = 2 to length[A] c 1 n 2. do key A[j] c 2 n-1 3. //insert A[j] to sorted sequence A[1. . j-1] 0 n-1 4. i j-1 c 4 n-1 5. while i >0 and A[i]>key c 5 j=2 n tj 6. do A[i+1] A[i] c 6 j=2 n(tj – 1) 7. i i-1 c 7 j=2 n(tj – 1) 8. A[i+1] key c 8 n – 1 (tj is the number of times the while loop test in line 5 is executed for that value of j) The total time cost T(n) = sum of cost times in each line =c 1 n + c 2(n-1) + c 4(n-1) + c 5 j=2 n tj+ c 6 j=2 n (tj-1)+ c 7 j=2 n (tj-1)+ c 8(n-1)

Analyzing Insertion Sort • What can T be? § Best case -- inner loop body never executed § Worst case -- inner loop body executed for all previous elements § Average case o ? ? ?

Analysis of Insertion Sort (cont. ) • Best case cost: already ordered numbers § tj=1, and line 6 and 7 will be executed 0 times • § T(n) = c 1 n + c 2(n-1) + c 4(n-1) + c 5(n-1) + c 8(n-1) =(c 1 + c 2 + c 4 + c 5 + c 8)n – (c 2 + c 4 + c 5 + c 8) = cn + c‘ Worst case cost: reverse ordered numbers § tj=j, § so j=2 n tj = j=2 n j =n(n+1)/2 -1, and j=2 n(tj – 1) = j=2 n(j – 1) = n(n-1)/2, • and § T(n) = c 1 n + c 2(n-1) + c 4(n-1) + c 5(n(n+1)/2 -1) + + c 6(n(n-1)/2 -1) + c 7(n(n -1)/2)+ c 8(n-1) =((c 5 + c 6 + c 7)/2)n 2 +(c 1 + c 2 + c 4 +c 5/2 -c 6/2 -c 7/2+c 8)n-(c 2 + c 4 + c 5 + c 8) =an 2+bn+c Average case cost: random numbers § in average, tj = j/2. T(n) will still be in the order of n 2, same as the worst case. 44

Insertion Sort Is O(n 2) • Proof § Suppose runtime is an 2 + bn + c o If any of a, b, and c are less than 0 replace the constant with its absolute value § an 2 + bn + c (a + b + c)n 2 + (a + b + c)n + (a + b + c) § 3(a + b + c)n 2 for n 1 § Let c’ = 3(a + b + c) and let n 0 = 1

Big O Fact • • A polynomial of degree k is O(nk) Proof: § Suppose f(n) = bknk + bk-1 nk-1 + … + b 1 n + b 0 o Let ai = | bi | § f(n) aknk + ak-1 nk-1 + … + a 1 n + a 0
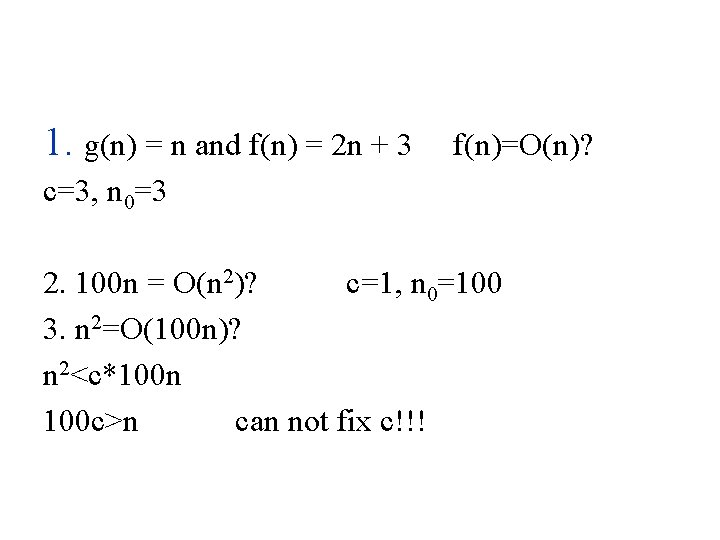
1. g(n) = n and f(n) = 2 n + 3 f(n)=O(n)? c=3, n 0=3 2. 100 n = O(n 2)? c=1, n 0=100 3. n 2=O(100 n)? n 2<c*100 n 100 c>n can not fix c!!!
![Linear search Searches an unordered array of integers int searchint data int n Linear search // Searches an unordered array of integers int search(int data[], int n,](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-48.jpg)
Linear search // Searches an unordered array of integers int search(int data[], int n, int value){ / for(int index = 0; index < n; index++){ if(data[index] == value) return index; } return -1; } T(n)=O(n)
![Bubble sort void bubble Sort int A int n for Bubble sort void bubble. Sort ( int A[] , int n ) { for](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-49.jpg)
Bubble sort void bubble. Sort ( int A[] , int n ) { for (i=0; i<n; i++) { for (j=i+1; j<n; ++j) [n, n-1, …. , 2] { if (A[j] > A[j+1]) [n-1, n-2, …. , 1] { t = A[j]; A[j] = A[j+1]; A[j+1] = t; } T(n)=c 1[n+(n-1)+(n-2)+… 2]+c 2[(n-1)+(n 2). . +1]=an 2+bn+c=O(n 2) }

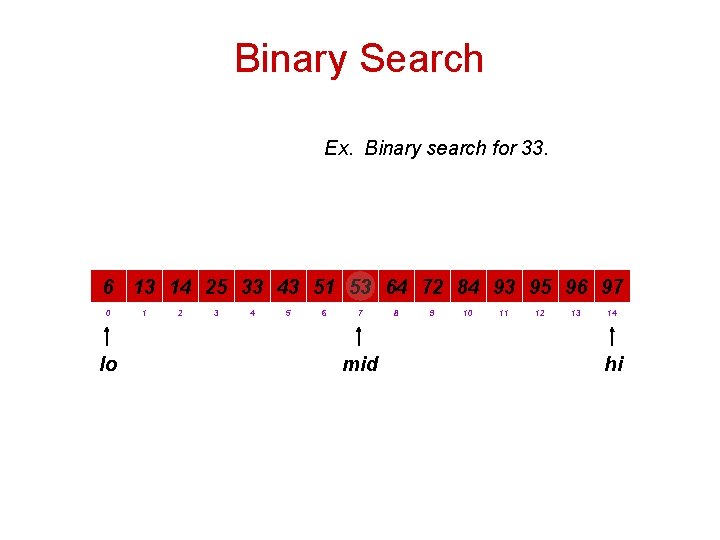
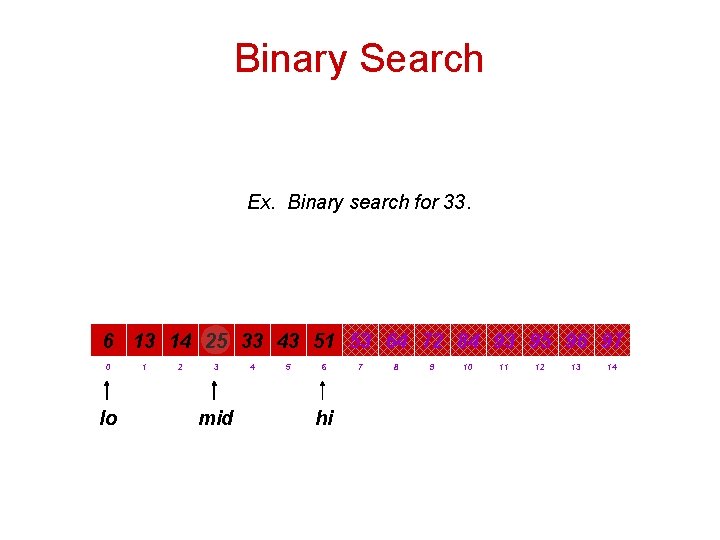
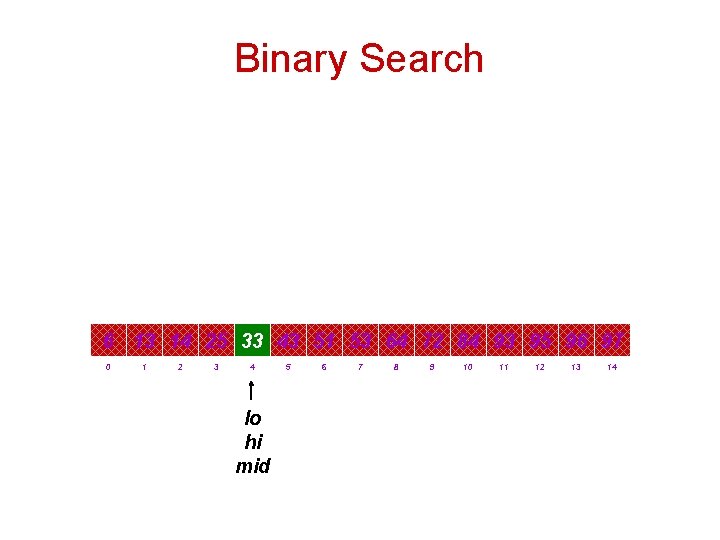
Binary Search Ex. Binary search for 33. 6 13 14 25 33 43 51 53 64 72 84 93 95 96 97 0 lo 1 2 3 4 5 6 7 mid 8 9 10 11 12 13 14 hi

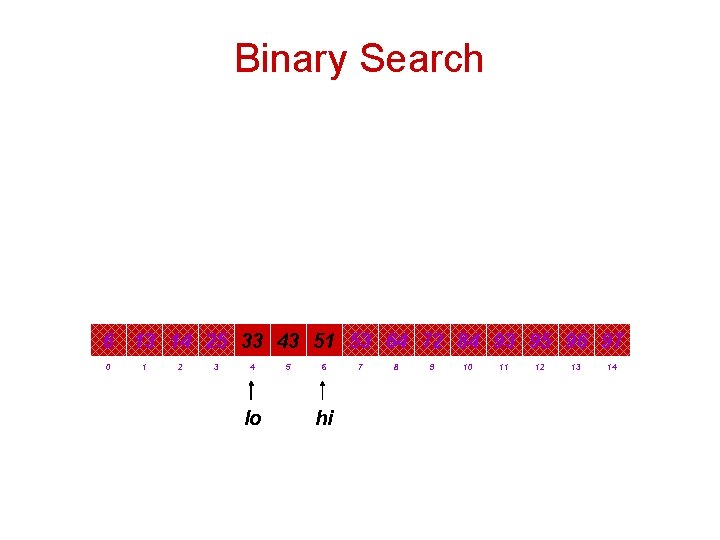
Binary Search Ex. Binary search for 33. 6 13 14 25 33 43 51 53 64 72 84 93 95 96 97 0 lo 1 2 3 4 5 6 hi 7 8 9 10 11 12 13 14

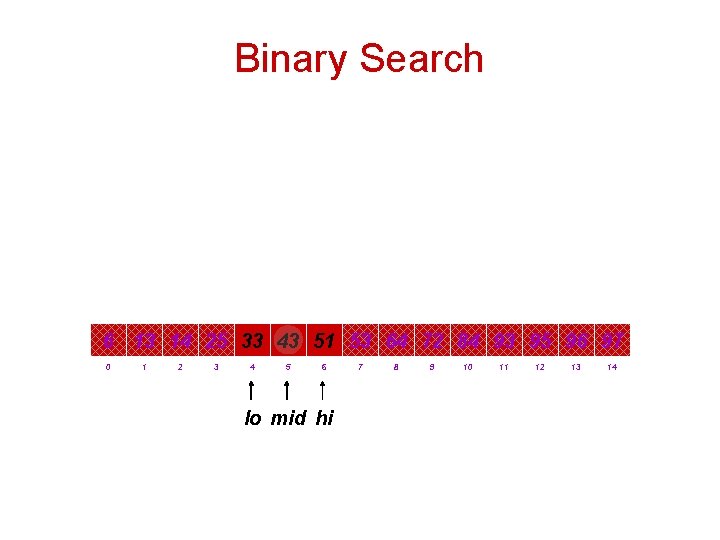
Binary Search Ex. Binary search for 33. 6 13 14 25 33 43 51 53 64 72 84 93 95 96 97 0 lo 1 2 3 mid 4 5 6 hi 7 8 9 10 11 12 13 14

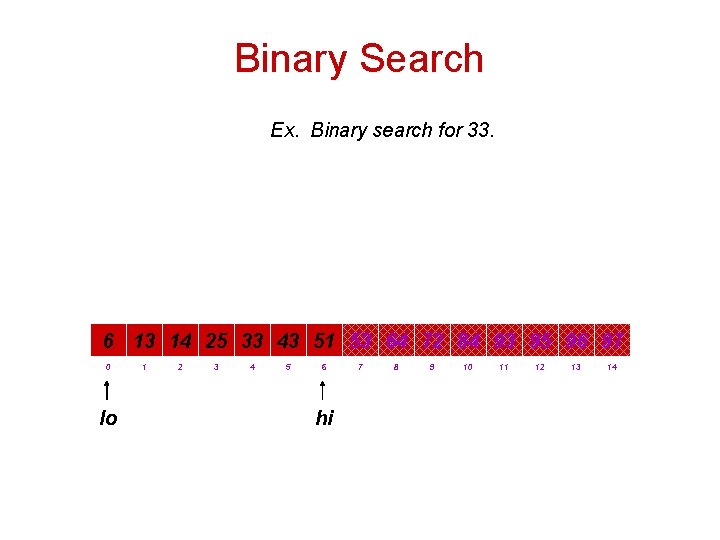
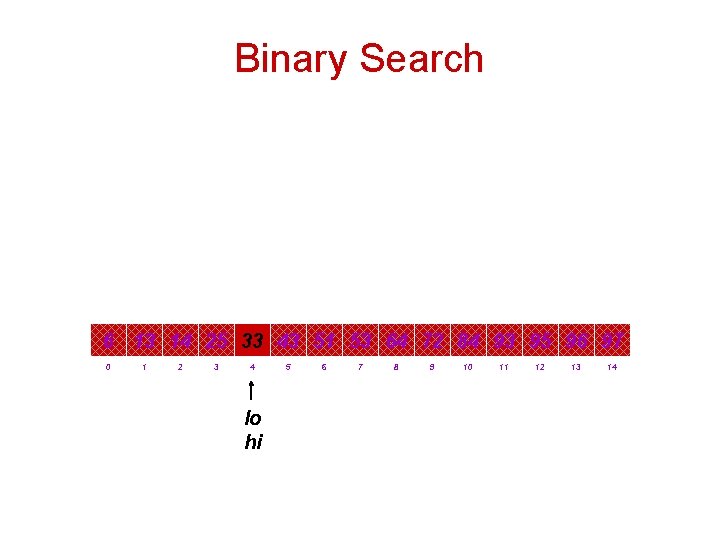
Binary Search 6 13 14 25 33 43 51 53 64 72 84 93 95 96 97 0 1 2 3 4 lo 5 6 hi 7 8 9 10 11 12 13 14

Binary Search 6 13 14 25 33 43 51 53 64 72 84 93 95 96 97 0 1 2 3 4 5 6 lo mid hi 7 8 9 10 11 12 13 14

Binary Search 6 13 14 25 33 43 51 53 64 72 84 93 95 96 97 0 1 2 3 4 lo hi 5 6 7 8 9 10 11 12 13 14

Binary Search 6 13 14 25 33 43 51 53 64 72 84 93 95 96 97 0 1 2 3 4 lo hi mid 5 6 7 8 9 10 11 12 13 14

Binary Search 6 13 14 25 33 43 51 53 64 72 84 93 95 96 97 0 1 2 3 4 lo hi mid 5 6 7 8 9 10 11 12 13 14
![Non recursive int bin Search int A int n int x Non recursive int bin. Search ( int A[] , int n , int x](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-58.jpg)
Non recursive int bin. Search ( int A[] , int n , int x ) { int L, R, M; L = 0; R = n-1; c 1 while (L < R) (k+1)*c 2 { M = (L + R) / 2; c 3*k if (x > A[M]) c 4*k L = M+1; c 5*k else R = M; c 6*k } return (A[L] == x); c 7 } T(n)=c 1+(k+1)*c 2+(c 3+c 4+c 5+c 6)*k+c 7 =k*C’+C’’=C’*log n+C’’=O(log n) n=2 k

Recursive function • Running time can be expressed as the recurrence relation • • First compute the recurrence relation Next, solve the recurrence relation using substitution method
![Recursive int binaryint a int n int m int l int u int mid Recursive int binary(int a[], int n, int m, int l, int u){ int mid,](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-60.jpg)
Recursive int binary(int a[], int n, int m, int l, int u){ int mid, c=0; if(l<=u){ mid=(l+u)/2; if(m==a[mid]){ c=1; } else if(m<a[mid]){ return binary(a, n, m, l, mid-1); } else return binary(a, n, m, mid+1, u); } else return c; } Recurrence relation T(n)=T(n/2)+c

Recursive • Solving recurrences Recurrence relation T(n)=T(n/2)+c § Substitution method T(n/2)=T(n/4)+c T(n/4)=T(n/8)+c …………. . T(n/2(k-1))=T(n/2 k)+c=T(1)+c T(n)=c+c+c……. +c + T(1) k times =kc+c 1=c*log(n)+c 1=O(log(n)) n=2 k

Factorial int factorial. Iter ( int n ) cost times { int prod, i; c 1 1 if (n <= 1) c 2 1 return 1; c 3 1 prod = 1; c 4 1 for (i=2; i<=n; ++i) c 5 n prod *= i; c 6 n-1 return prod; c 7 1 } T(n)=c 1+c 2+. . +n*c 5+(n-1)*c 6+c 7=an+b=O(n)

Recursive version int factorial. Rec ( int n ) { int x; if (n <= 1) return 1; x=n * factorial. Rec(n-1); return x } Recurrence relation T(0)=C 1; T(1)=C 1 T(n)= C 2+T(n-1) n>1

Solving recurrences T(n)= C 2+T(n-1)=C 2+T(n-2) T(n)=C 2+T(n-2)=C 2+T(n-3) T(n)=C 2+T(n-2) =C 2+C 2+T(n-3) After n-1 number of steps T(n)=(n-1)C 2+T(1) =(n-1)C 2+C 1 =an+b =O(n)

Mergesort

Basic Idea • • Divide the array into two halves Sort the two sub-arrays Merge the two sorted sub-arrays into a single sorted array Step 2 (sorting the sub-arrays) is done recursively (divide in two, sort, merge) until the array has a single element (base condition of recursion)

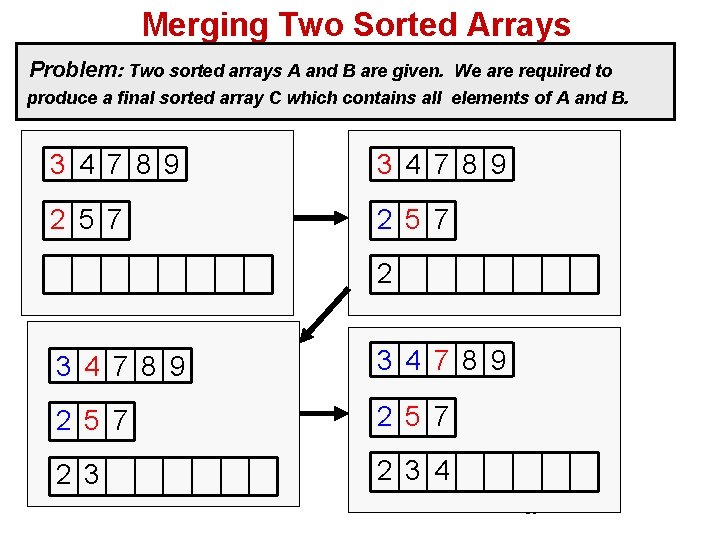
Merging Two Sorted Arrays Problem: Two sorted arrays A and B are given. We are required to produce a final sorted array C which contains all elements of A and B. 3 4 7 8 9 2 5 7 2 3 4 67

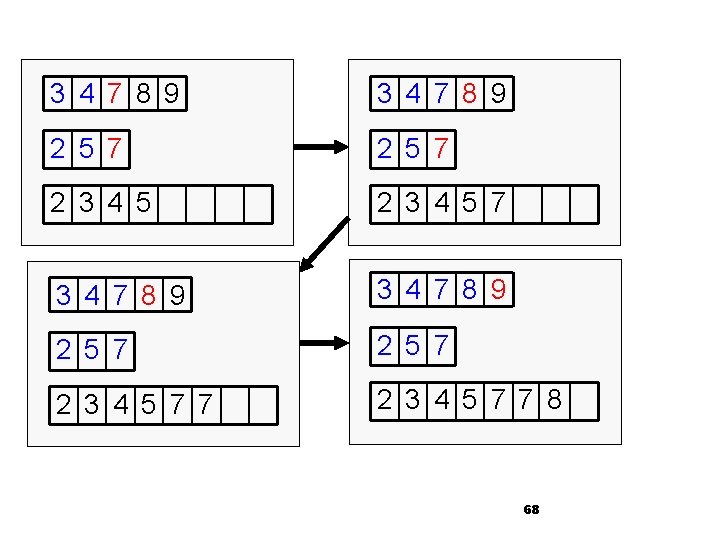
3 4 7 8 9 2 5 7 2 3 4 5 7 7 8 68

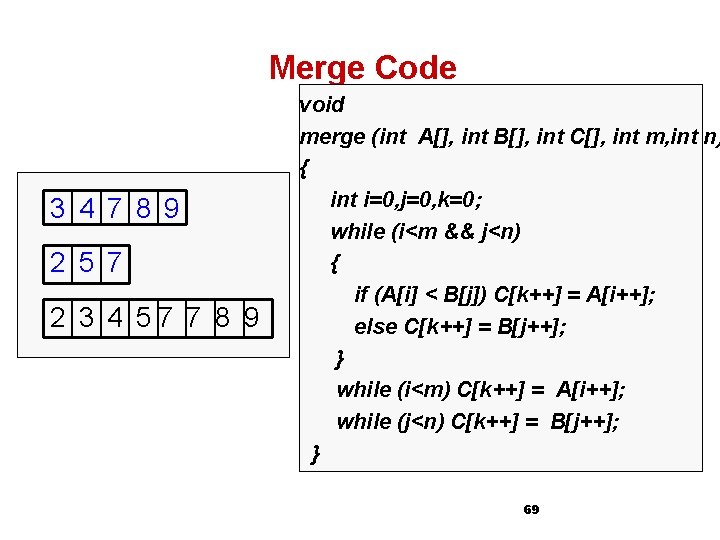
Merge Code 3 4 7 8 9 2 5 7 2 3 4 57 7 8 9 void merge (int A[], int B[], int C[], int m, int n) { int i=0, j=0, k=0; while (i<m && j<n) { if (A[i] < B[j]) C[k++] = A[i++]; else C[k++] = B[j++]; } while (i<m) C[k++] = A[i++]; while (j<n) C[k++] = B[j++]; } 69
![Merge Sort Sorting an array recursively void mergesort int A int n int Merge Sort: Sorting an array recursively void mergesort (int A[], int n) { int](https://slidetodoc.com/presentation_image_h/1ba3c4d9eb6b4eb8103c9875837fe04d/image-70.jpg)
Merge Sort: Sorting an array recursively void mergesort (int A[], int n) { int i, j, B[max]; if (n <= 1) return; i = n/2; mergesort(A, i); mergesort(A+i, n-i); merge(A, A+i, B, i, n-i); for (j=0; j<n; j++) A[j] = B[j]; free(B); } Recurrence relation T(1) = C 1, T(n) = 2 T(n/2) + cn + d 70

Solving recurrences T(n) = 2 T(n/2) + cn + d T(n/2)=2 T(n/4)+cn/2+d T(n)=2(2 T(n/4)+cn/2+d)+cn+d =4 T(n/4)+cn+2 d+cn+d =4 T(n/4)+2 cn+3 d After k steps T(n)=2 k. T(n/2 k) + kcn+C’d =n. T(1)+nlog(n)+C 2’ =C 1*n+nlog(n)+C 2’=O(nlogn) n=2 k
 Asymptotic performance
Asymptotic performance Asymptotic complexity analysis
Asymptotic complexity analysis Big o notation if else statement
Big o notation if else statement Asymptotic analysis
Asymptotic analysis F(n) ≥ g(n) adalah notasi jenis
F(n) ≥ g(n) adalah notasi jenis Aep information theory
Aep information theory Recurrence relation cheat sheet
Recurrence relation cheat sheet Compare asymptotic growth rate
Compare asymptotic growth rate Asymptotic lower bound
Asymptotic lower bound Notasi omega
Notasi omega Asymptotically tight bound
Asymptotically tight bound Asymptotic notation graph
Asymptotic notation graph Asymptotic freedom
Asymptotic freedom Asymptotic runtime
Asymptotic runtime Small omega notation
Small omega notation Design and analysis of algorithms syllabus
Design and analysis of algorithms syllabus An introduction to the analysis of algorithms
An introduction to the analysis of algorithms What is analysis of algorithm
What is analysis of algorithm Association analysis: basic concepts and algorithms
Association analysis: basic concepts and algorithms Input and output algorithm
Input and output algorithm Analysis of algorithms
Analysis of algorithms Algorithm analysis examples
Algorithm analysis examples Fundamentals of analysis of algorithm efficiency
Fundamentals of analysis of algorithm efficiency Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Probabilistic analysis and randomized algorithms
Probabilistic analysis and randomized algorithms Design and analysis of algorithms introduction
Design and analysis of algorithms introduction Analysis of algorithms lecture notes
Analysis of algorithms lecture notes Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Goals of analysis of algorithms
Goals of analysis of algorithms Exercise 24
Exercise 24 Binary search in design and analysis of algorithms
Binary search in design and analysis of algorithms Introduction to the design and analysis of algorithms
Introduction to the design and analysis of algorithms Competitive analysis algorithms
Competitive analysis algorithms Design and analysis of algorithms
Design and analysis of algorithms Design and analysis of algorithms
Design and analysis of algorithms Cluster analysis basic concepts and algorithms
Cluster analysis basic concepts and algorithms Comp 482
Comp 482 Chapter review motion part a vocabulary review answer key
Chapter review motion part a vocabulary review answer key Writ of certiorari ap gov example
Writ of certiorari ap gov example Narrative review vs systematic review
Narrative review vs systematic review What is inclusion and exclusion criteria
What is inclusion and exclusion criteria Narrative review vs systematic review
Narrative review vs systematic review Explain performance counselling
Explain performance counselling Self appraisal integrity
Self appraisal integrity Performance review institute
Performance review institute Introductory performance review
Introductory performance review Arizona judicial performance review
Arizona judicial performance review Rpms meaning
Rpms meaning Performance review introduction example
Performance review introduction example Performance review committee enron
Performance review committee enron Performance review institute
Performance review institute Computational thinking algorithms and programming
Computational thinking algorithms and programming Types of algorithm
Types of algorithm Recursive algorithms
Recursive algorithms Handling patients
Handling patients Recursion java
Recursion java Types of randomized algorithms
Types of randomized algorithms Process mining algorithms
Process mining algorithms Evolution of logistics ppt
Evolution of logistics ppt Nature-inspired learning algorithms
Nature-inspired learning algorithms Metaheuristic algorithms
Metaheuristic algorithms Making good encryption algorithms
Making good encryption algorithms Statistical algorithms
Statistical algorithms Professor ajit diwan
Professor ajit diwan Disadvantages of greedy algorithm
Disadvantages of greedy algorithm List of greedy algorithms
List of greedy algorithms Consistent global state
Consistent global state Classical algorithms for forrelation
Classical algorithms for forrelation Aprioti
Aprioti Dsp algorithms tutorial
Dsp algorithms tutorial Distributed algorithms nancy lynch
Distributed algorithms nancy lynch