Orientao Tcnica O uso do Algeplan como recurso

Orientação Técnica – “O uso do Algeplan como recurso facilitador da aprendizagem na unidade temática Álgebra” Diretoria de Ensino Região de Piracicaba PCNPs Patricia C. Malaguetta Sueli Ap. Gobbo Araujo 06 e 09/05/2019

O Dia Nacional da Matemática é comemorado no dia 6 de maio em homenagem ao dia de nascimento de Malba Tahan. A intenção é: Divulgar a Matemática como área de conhecimento; Sua história; Suas aplicações no mundo; Sua ligação com outras áreas de conhecimento; e Derrubar o mito de que aprender Matemática é difícil e privilégio de poucos. Foi instituído pelo projeto de Lei n. 3. 482/2004, de autoria da deputada professora Raquel Teixeira. O Prof. Júlio César de Melo e Souza que usou o heterônimo: Malba Tahan, Nasceu em 06 de maio de 1895 no Rio de Janeiro – RJ Morreu em 18 de junho de 1974 em Recife – PE, aos 79 anos.

Se quisermos que as crianças se tornem bons matemáticos, precisamos demonstrar para elas que a matemática é divertida e útil e que pode ser uma atividade sociável e cooperativa, assim como uma atividade tranquila e individual. [. . . ]. As crianças estabelecerão desafios mais difíceis para si mesmas se dermos a elas o controle de sua aprendizagem em vez de deixá-las nas mãos dos adultos. (GRIFFITHS, 1994, p. 183).

Objetivos: - Apresentar metodologia diferenciada para o ensino da álgebra; - Desenvolver por meio de oficinas uma abordagem concreta para os conteúdos de álgebra e geometria, trazendo a relação entre ambos como forma de melhoria na aprendizagem da matemática; - Trabalhar os conceitos e operações envolvendo monômios e polinômios; - Trabalhar equação do 2º grau por meio de material concreto.

MMR – Ação: Formar os professores de matemática para atender as necessidades dos alunos na unidade temática Álgebra

IDESP 2019 - Metas da DER Piracicaba EFAI – 6, 75 EFAF – 3, 95 EM – 2, 93

Segundo Miguel (2003 apud PASQUETTI, 2008, p. 13), uma das ações que podem ser realizadas na tentativa de superar o desinteresse dos alunos diz respeito ao material concreto e aos jogos, instrumentos que podem favorecer a aprendizagem de conteúdos matemáticos para esses alunos com dificuldades de aprendizagem.

[. . . ] Convém também salientar que a “visualização” de expressões algébricas, por meio do cálculo de áreas e perímetros de retângulos, é um recurso que facilita a aprendizagem de noções algébricas como: Exemplo: 1º) Cálculo da área do retângulo pela multiplicação das dimensões do retângulo: a e a +2: a. (a+2) 2º) Cálculo da área do retângulo pela soma das áreas das figuras que o compõem, o quadrado e o retângulo menor: a²+2 a. Obtendo-se assim a. (a +2)= a² + 2 a (BRASIL, 1997, p. 121)

A utilização desses recursos possibilita ao aluno conferir um tipo de significado às expressões. No entanto, a interpretação geométrica dos cálculos algébricos é limitada, pois nem sempre se consegue um modelo geométrico simples para aplicá-lo. Além disso, é preciso que ele perceba que é possível atribuir outros significados às expressões. Assim, ‘visualizações’ desse tipo podem ser interessantes em alguns momentos, dependendo do contexto da situação problema, mas o trabalho não pode apoiar-se exclusivamente nelas. (BRASIL, 1997, p. 121).

[. . . ] podemos reafirmar que o Algeplan apesar de manter semelhanças com a Álgebra e com a Geometria, possui suas regras de significação constituindo-se em um jogo de linguagem que deverá ser aprendido, tanto quanto a Álgebra ou a própria Geometria. (POLETO, 2010, p. 49) Diante disso perguntamo-nos: uma criança que domine as técnicas algorítmicas de operações com expressões algébricas também dominará as regras do Algeplan? E aquela que entender as regras de uso do material, conseguirá transpô-las para o manuseio algorítmico das expressões? E quanto à Geometria, é necessário que a criança saiba as relações de área para conseguir compreender as regras do Algeplan? (POLETO, 2010, p. 49)

O uso do material Algeplan como recurso metodológico Apresentação do Material

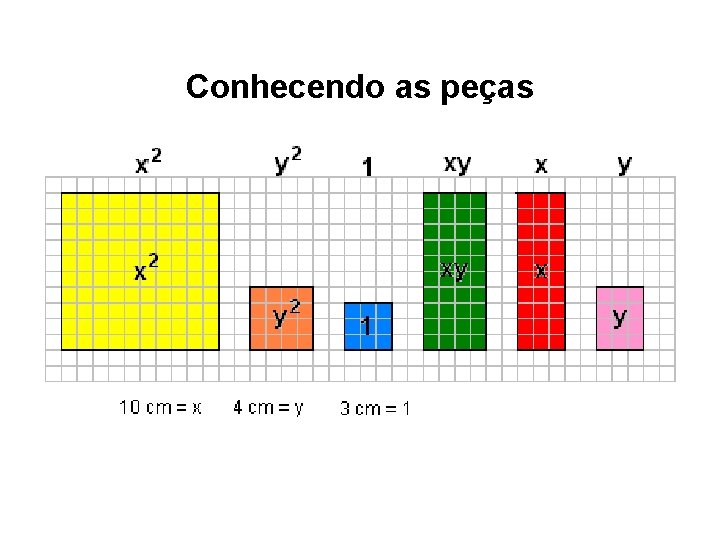
Conhecendo as peças

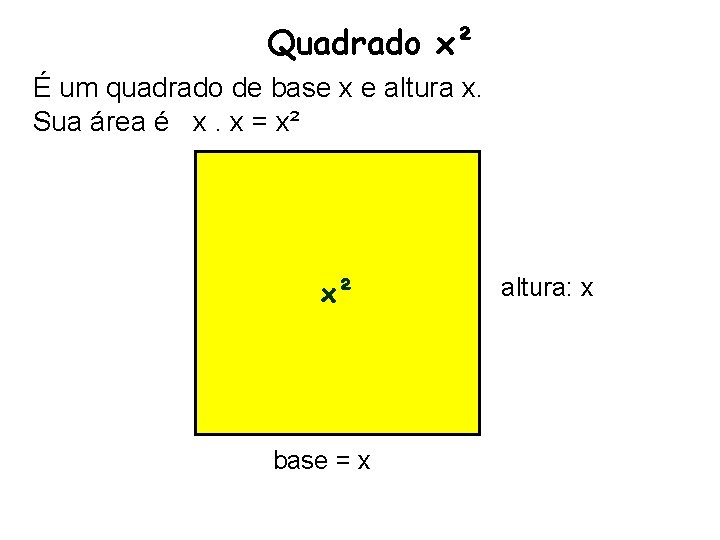
Quadrado x² É um quadrado de base x e altura x. Sua área é x. x = x² x² altura: x base = x

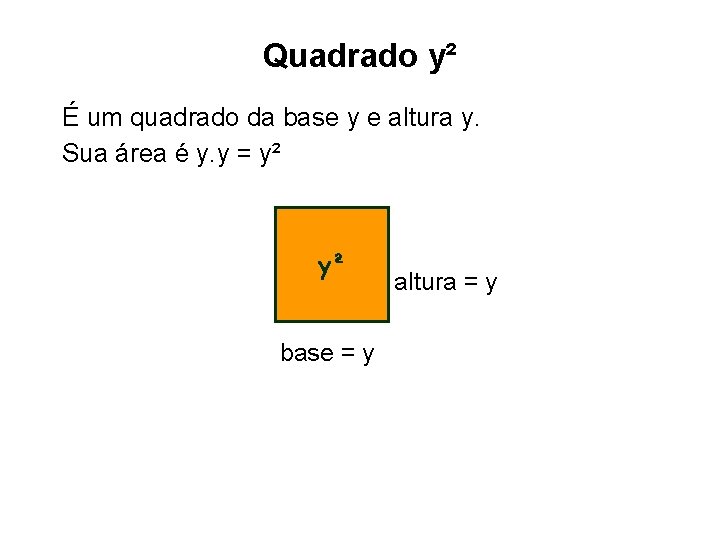
Quadrado y² É um quadrado da base y e altura y. Sua área é y. y = y² y² altura = y base = y

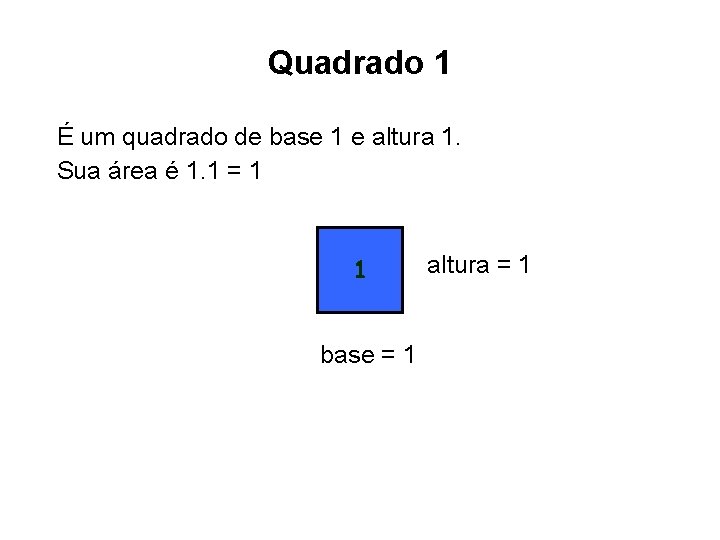
Quadrado 1 É um quadrado de base 1 e altura 1. Sua área é 1. 1 = 1 1 base = 1 altura = 1

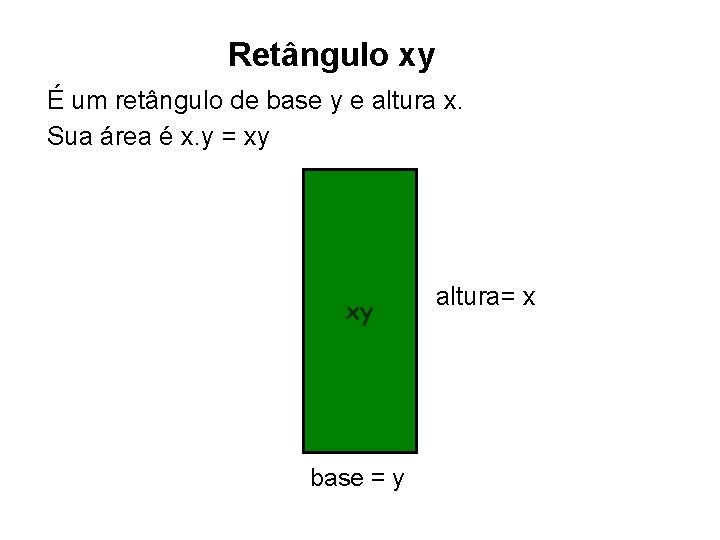
Retângulo xy É um retângulo de base y e altura x. Sua área é x. y = xy altura= x xy base = y

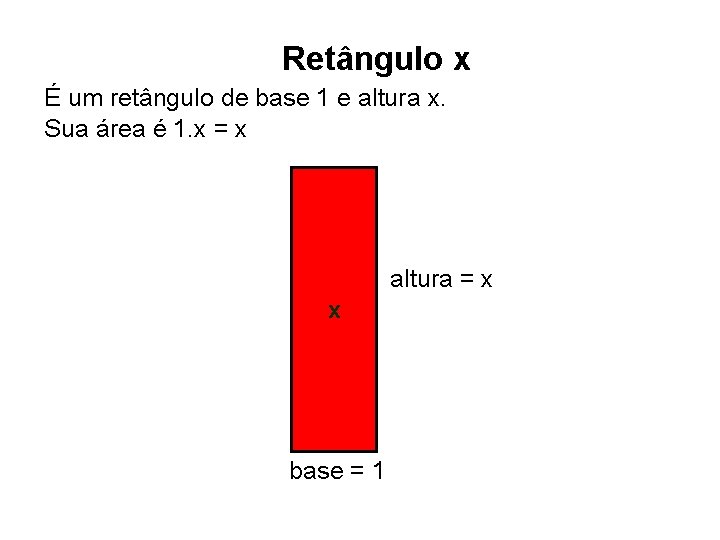
Retângulo x É um retângulo de base 1 e altura x. Sua área é 1. x = x altura = x x base = 1

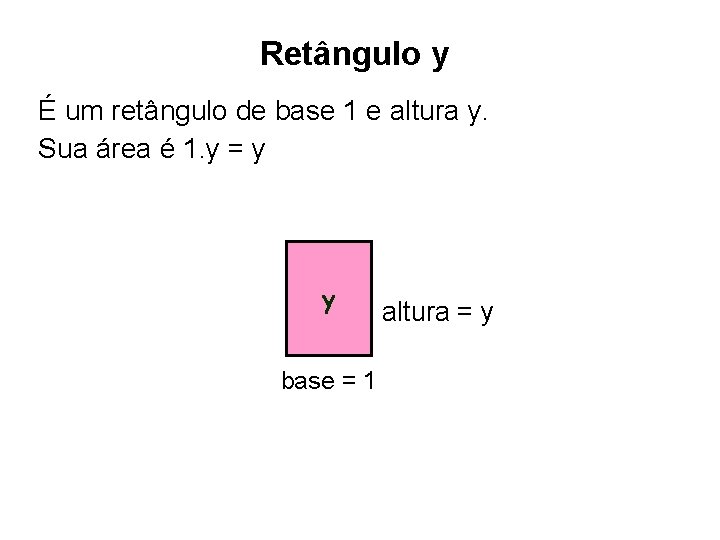
Retângulo y É um retângulo de base 1 e altura y. Sua área é 1. y = y y altura = y base = 1

Observações: • Na apresentação as peças brancas anulam as peças coloridas. • Com o material o verso das peças anulam as peças coloridas.

Operações com o uso do Algeplan

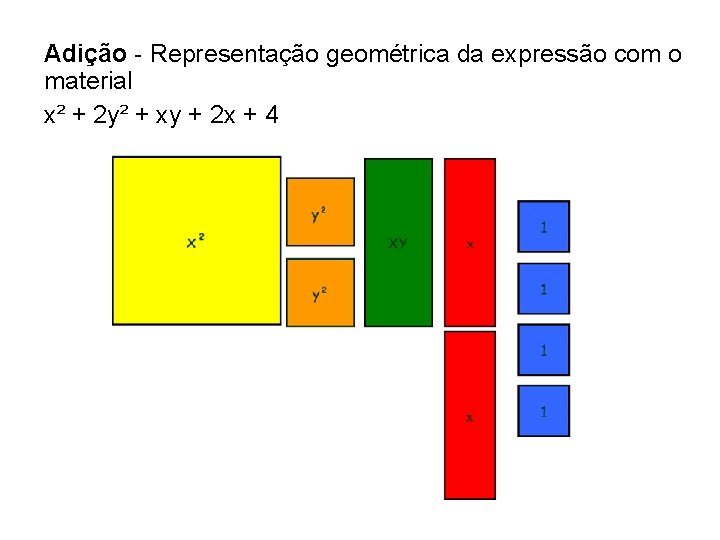
Adição - Representação geométrica da expressão com o material x² + 2 y² + xy + 2 x + 4

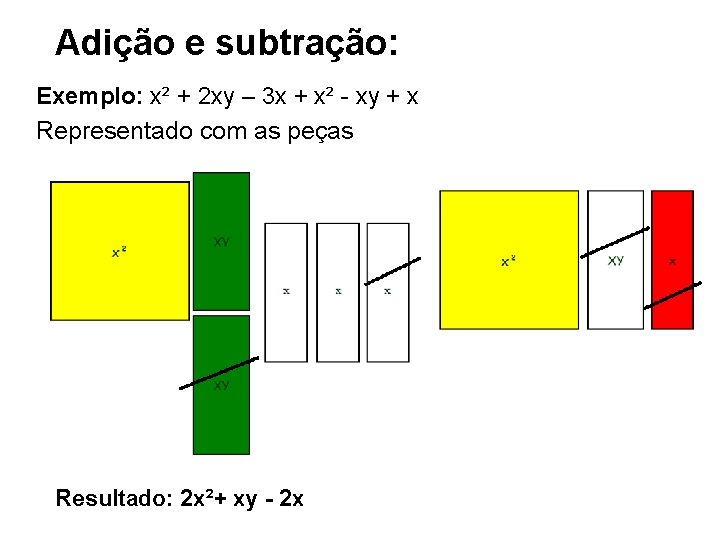
Adição e subtração: Exemplo: x² + 2 xy – 3 x + x² - xy + x Representado com as peças Resultado: 2 x²+ xy - 2 x

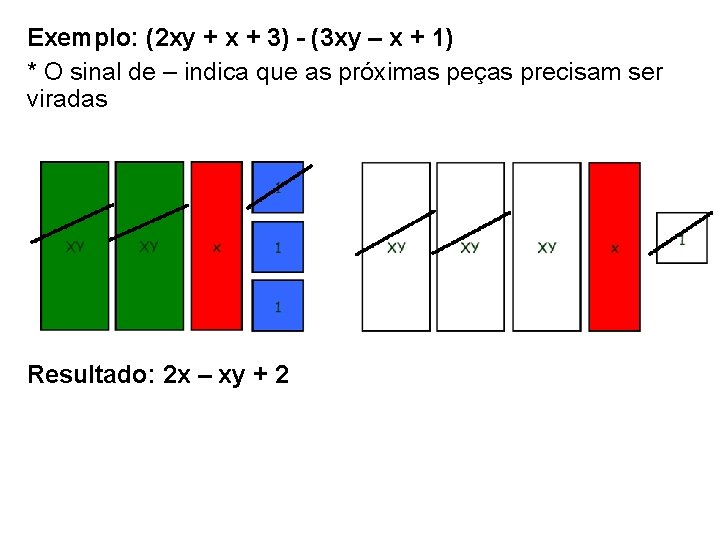
Exemplo: (2 xy + x + 3) - (3 xy – x + 1) * O sinal de – indica que as próximas peças precisam ser viradas Resultado: 2 x – xy + 2

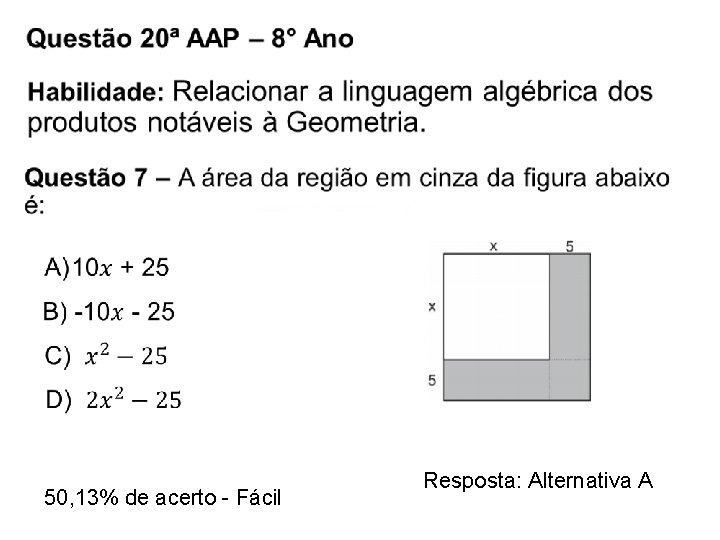
50, 13% de acerto - Fácil Resposta: Alternativa A

Habilidade: Realizar operações com polinômios. Podemos afirmar que A + B – C é igual a: 39, 66 % de acerto - Médio Resposta: Alternativa D

Sintetizando: • Representamos a operação com as figuras. • Agrupamos os termos semelhantes (mesma forma). • Somamos ou subtraímos os termos semelhantes. • Escrevemos o resultado ordenando os monômios observando a ordem decrescente dos expoentes.

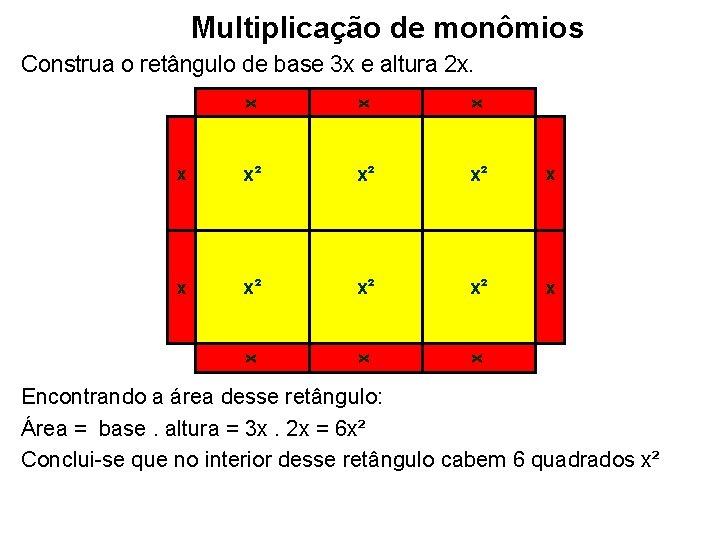
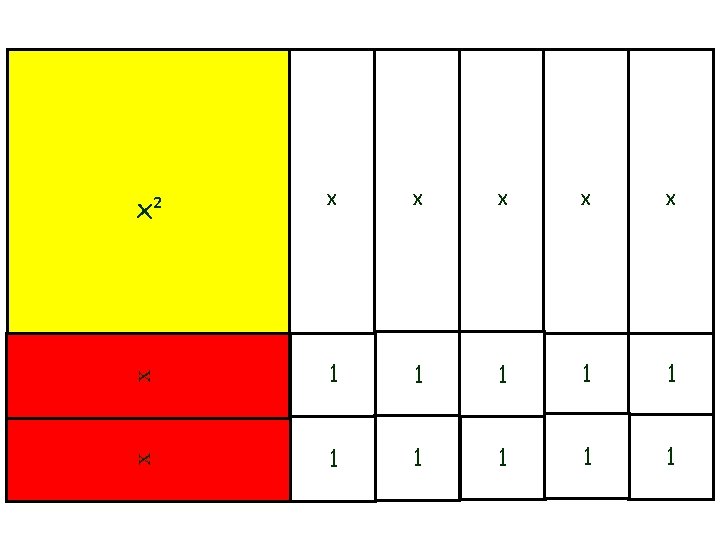
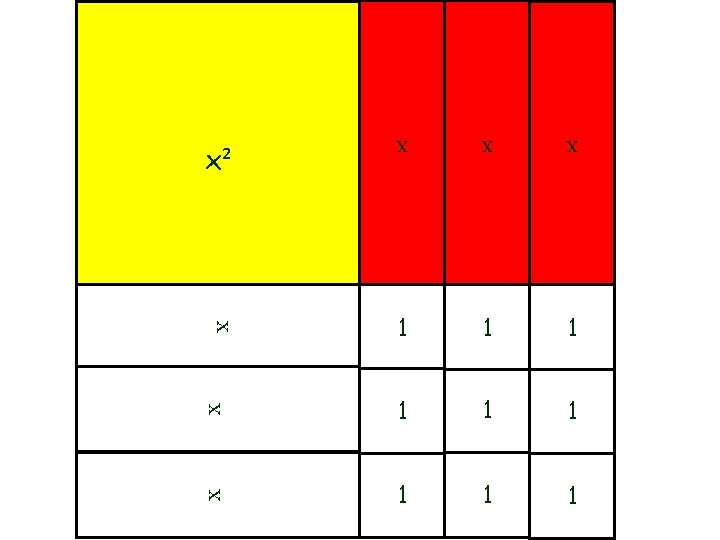
Multiplicação de monômios Construa o retângulo de base 3 x e altura 2 x. x x x² x² x² x x x x Encontrando a área desse retângulo: Área = base. altura = 3 x. 2 x = 6 x² Conclui-se que no interior desse retângulo cabem 6 quadrados x²

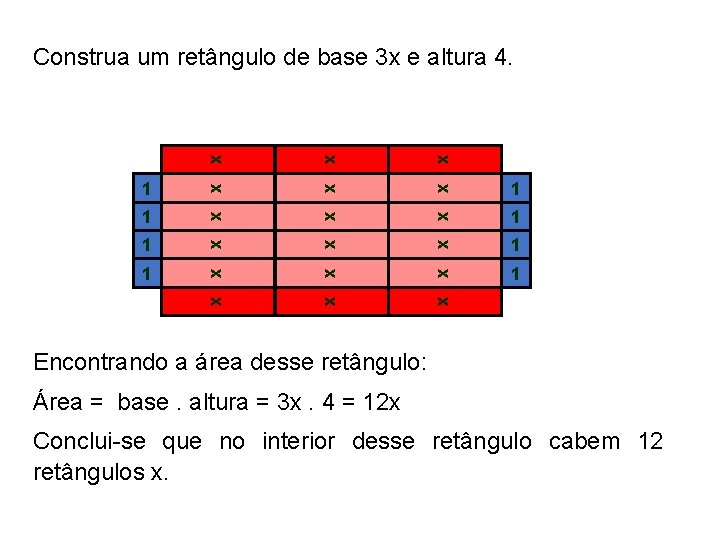
Construa um retângulo de base 3 x e altura 4. x x x 1 x 1 x x 1 Encontrando a área desse retângulo: Área = base. altura = 3 x. 4 = 12 x Conclui-se que no interior desse retângulo cabem 12 retângulos x.

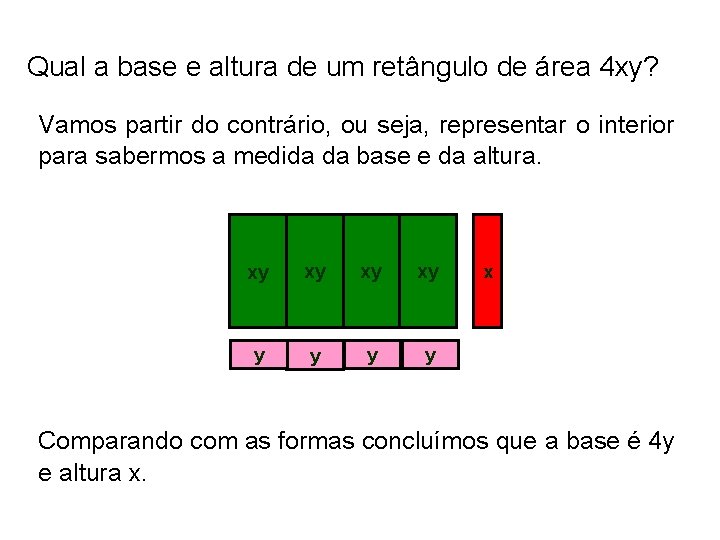
Qual a base e altura de um retângulo de área 4 xy? Vamos partir do contrário, ou seja, representar o interior para sabermos a medida da base e da altura. xy xy y y x Comparando com as formas concluímos que a base é 4 y e altura x.

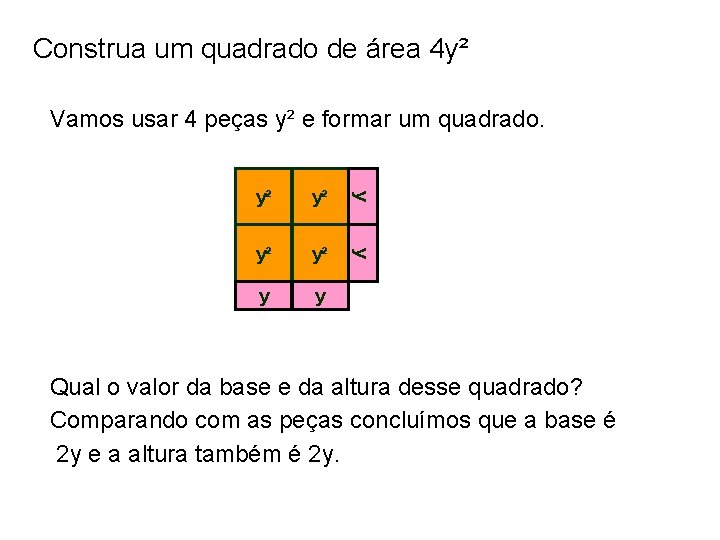
Construa um quadrado de área 4 y² Vamos usar 4 peças y² e formar um quadrado. y² y² y y y Qual o valor da base e da altura desse quadrado? Comparando com as peças concluímos que a base é 2 y e a altura também é 2 y.

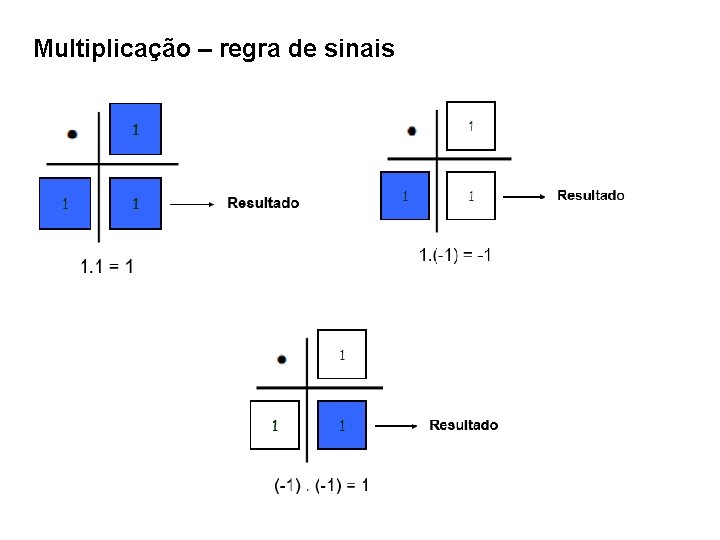
Multiplicação – regra de sinais

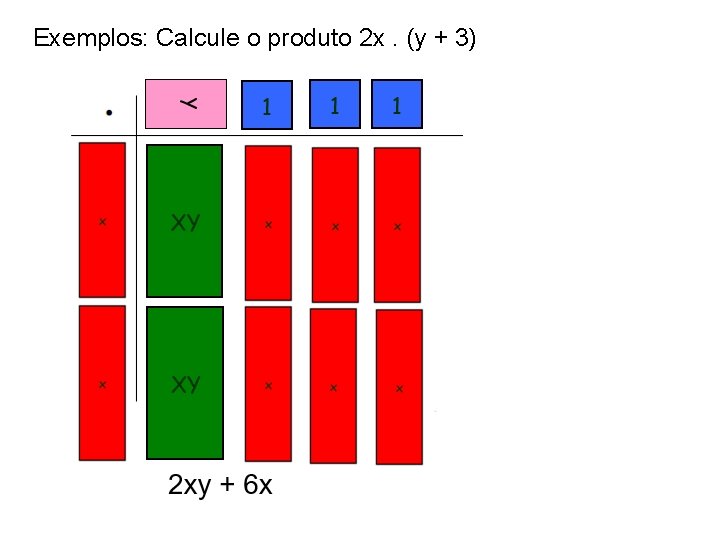
Exemplos: Calcule o produto 2 x. (y + 3)

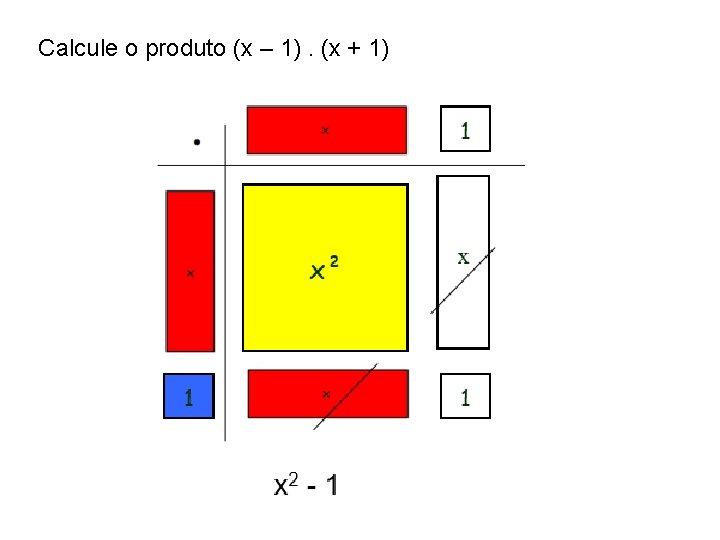
Calcule o produto (x – 1). (x + 1)

Questão 20ª AAP – 8° Ano Habilidade: Reconhecer equivalências entre expressões algébricas. Questão 3 - Ao simplificar a expressão 3(�� + �� ) − 7(�� − 2) − 4�� obtém-se: A) −�� − 6�� − 2 B) −�� − 4�� +14 C) −�� – 4�� − 14 D) �� − 4�� − 2 Resposta: Alternativa B 51, 49% de acerto - Fácil

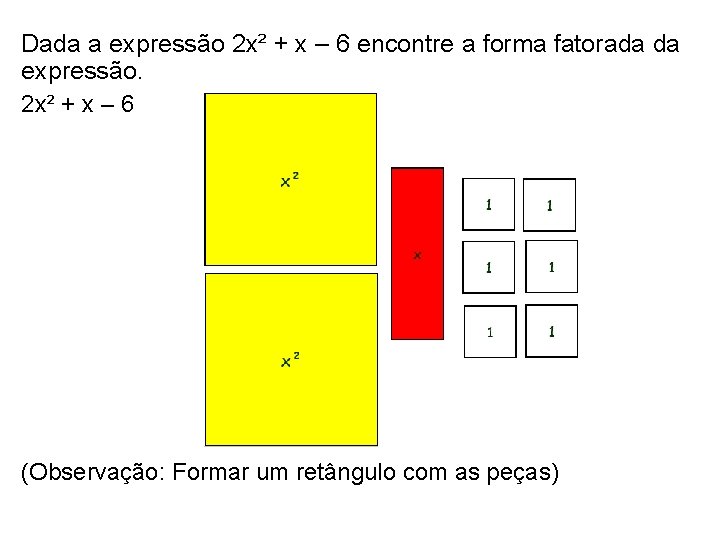
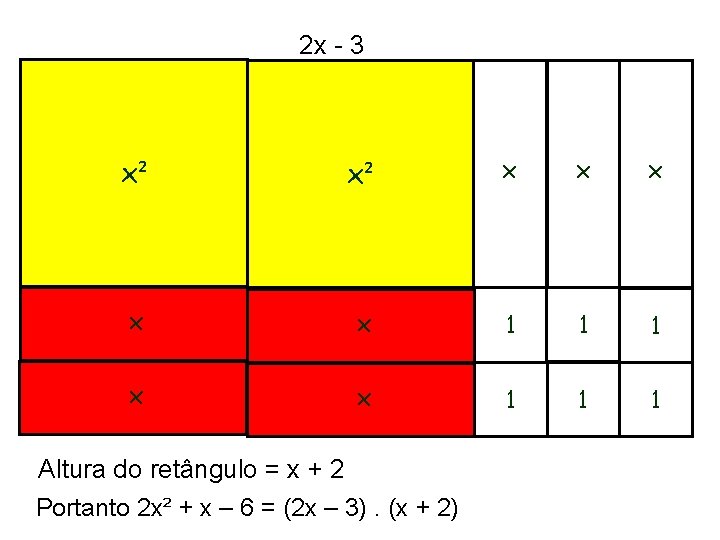
Dada a expressão 2 x² + x – 6 encontre a forma fatorada da expressão. 2 x² + x – 6 (Observação: Formar um retângulo com as peças)

x x x x² 1 1 1 x 2 x - 3 1 1 1 Altura do retângulo = x + 2 Portanto 2 x² + x – 6 = (2 x – 3). (x + 2)

Habilidade: Identificar os coeficientes e raízes de uma equação algébrica e as relações entre eles. 55, 15 % de acerto - Fácil Resposta: Alternativa E

Habilidade: Identificar os coeficientes e raízes de uma equação algébrica e as relações entre eles. A) S = - 4 e P = - 5 B) S = 4 e P = 5 C) S = 9 e P = 20 D) S = - 9 e P = - 20 E) S = - 9 e P = 20 43, 81 % de acerto - Fácil Resposta: Alternativa C

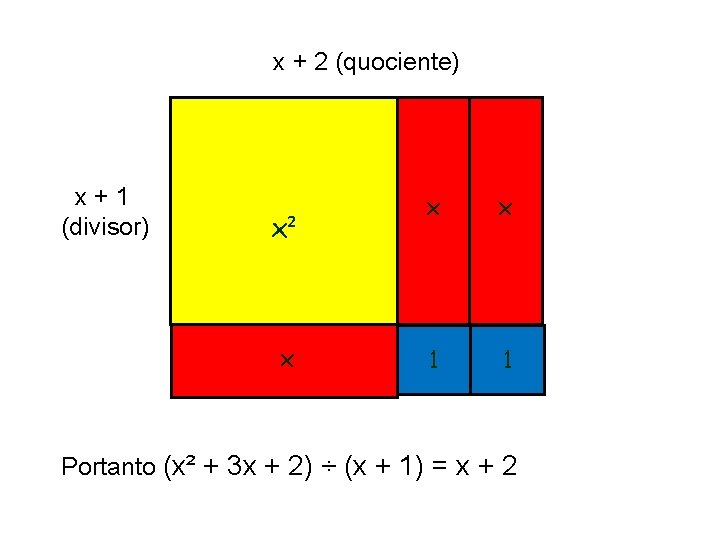
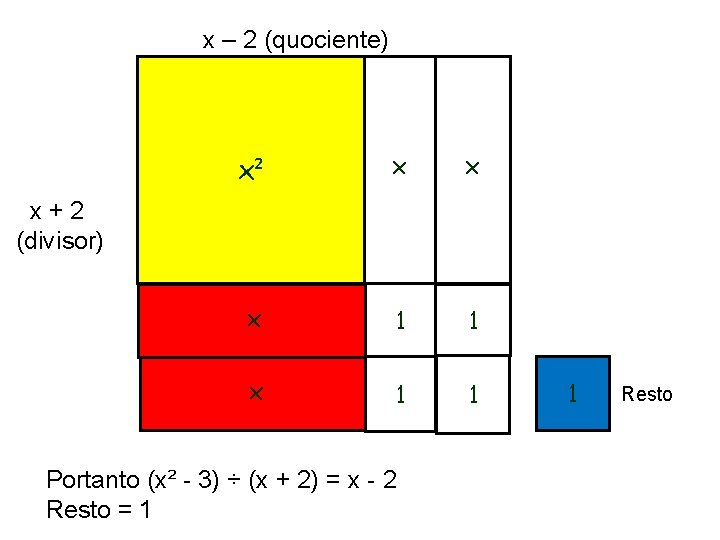
Divisão – Exata (o produto do quociente pelo divisor deverá ser igual ao dividendo) Exemplo 1: Resolva a divisão do polinômio (x² + 3 x + 2) pelo (x + 1) Observação: Utiliza-se o material para representar o dividendo (x² + 3 x + 2) formando um retângulo perfeito com um dos lados igual ao divisor (x + 1), assim o outro lado formado será o quociente.

x + 2 (quociente) x x x² x x + 1 (divisor) 1 1 Portanto (x² + 3 x + 2) ÷ (x + 1) = x + 2

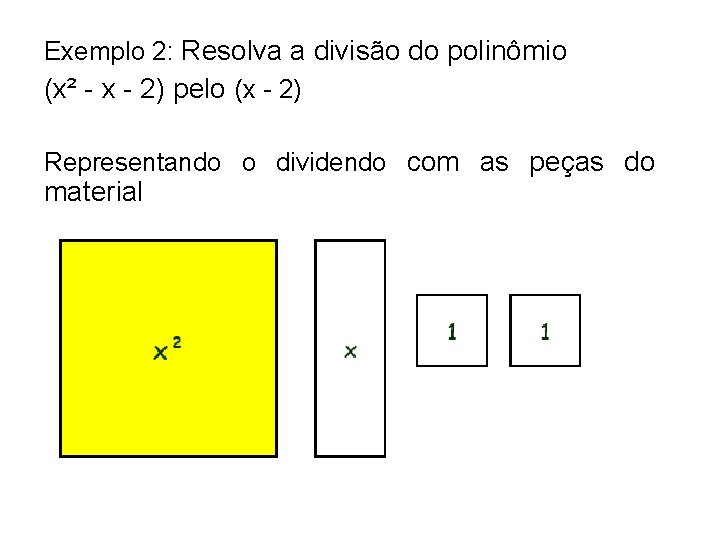
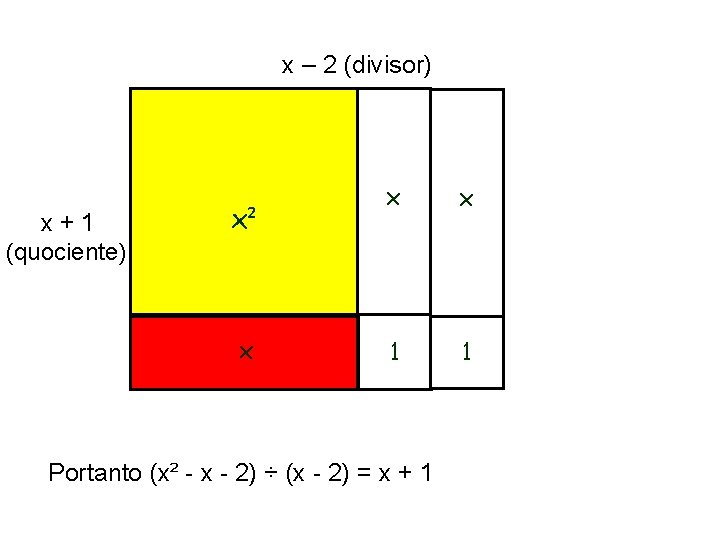
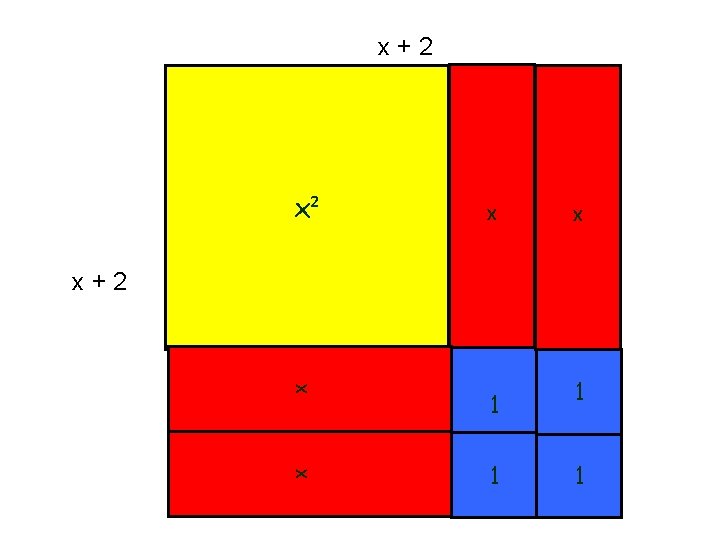
Exemplo 2: Resolva a divisão do polinômio (x² - x - 2) pelo (x - 2) Representando o dividendo com as peças do material

x² x x x + 1 (quociente) x x – 2 (divisor) 1 1 Portanto (x² - x - 2) ÷ (x - 2) = x + 1

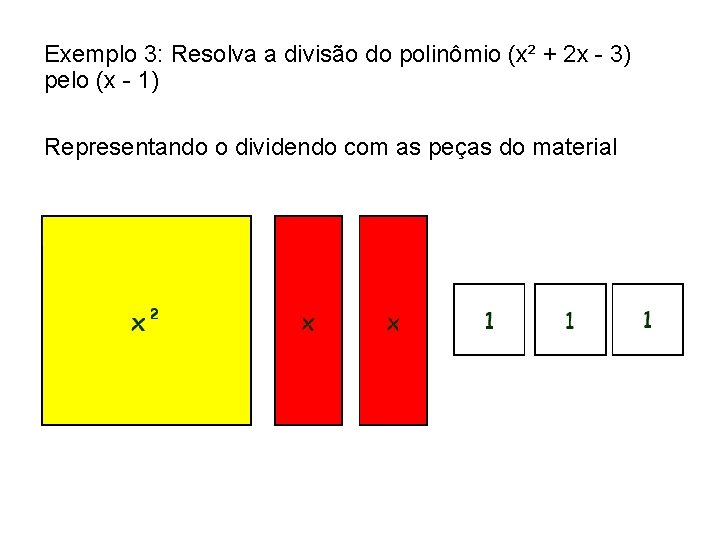
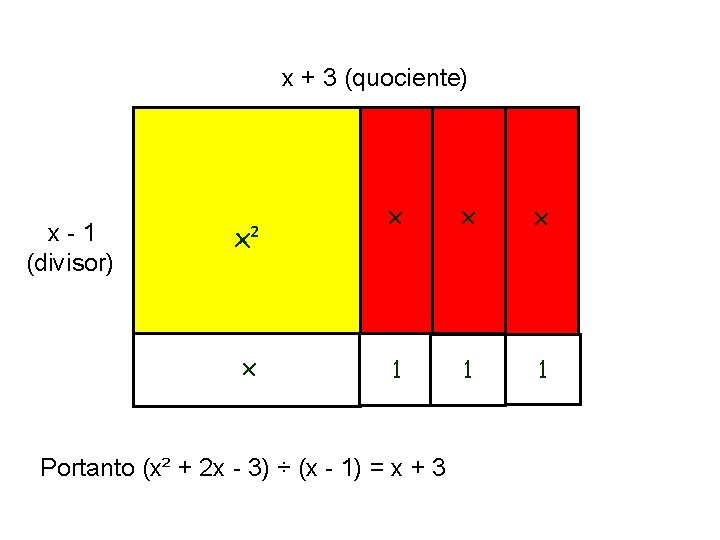
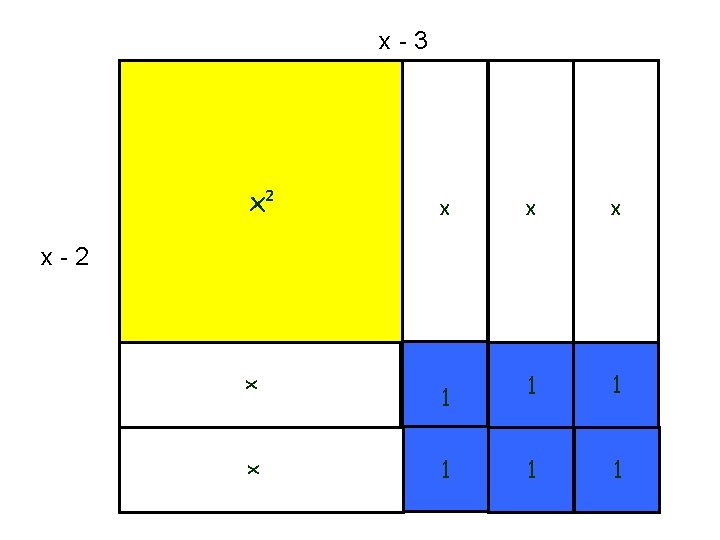
Exemplo 3: Resolva a divisão do polinômio (x² + 2 x - 3) pelo (x - 1) Representando o dividendo com as peças do material

x + 3 (quociente) x x x (divisor) x² x x - 1 1 1 1 Portanto (x² + 2 x - 3) ÷ (x - 1) = x + 3

Habilidade: Reconhecer equivalências entre expressões algébricas. Resposta: Alternativa B 32, 23% de acerto - Difícil

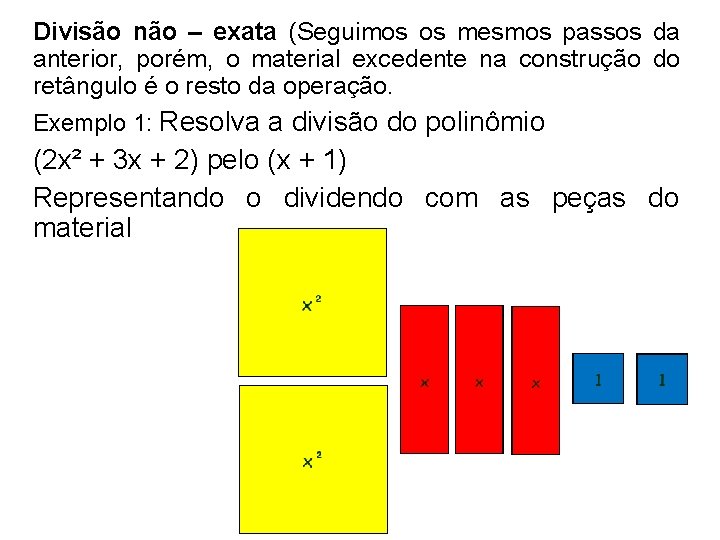
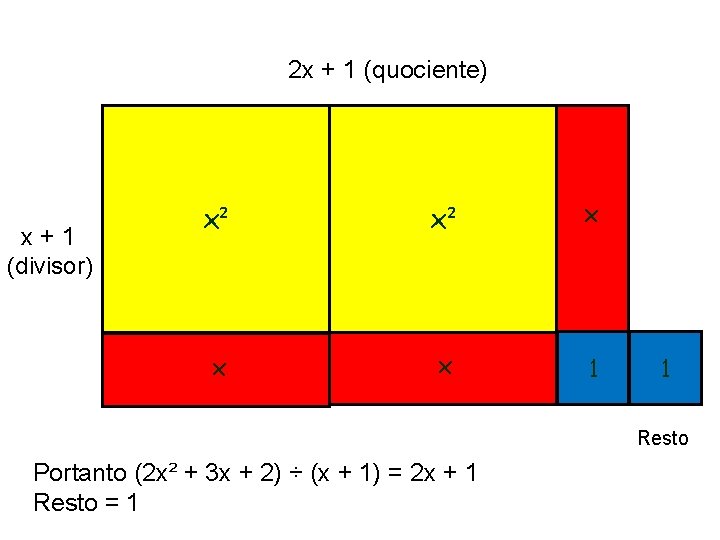
Divisão não – exata (Seguimos os mesmos passos da anterior, porém, o material excedente na construção do retângulo é o resto da operação. Exemplo 1: Resolva a divisão do polinômio (2 x² + 3 x + 2) pelo (x + 1) Representando o dividendo com as peças do material

x x² x x + 1 (divisor) x² x 2 x + 1 (quociente) 1 1 Resto Portanto (2 x² + 3 x + 2) ÷ (x + 1) = 2 x + 1 Resto = 1

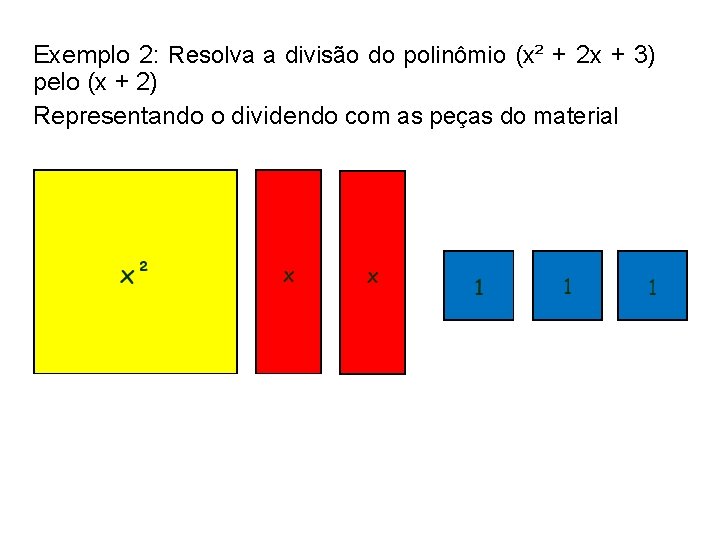
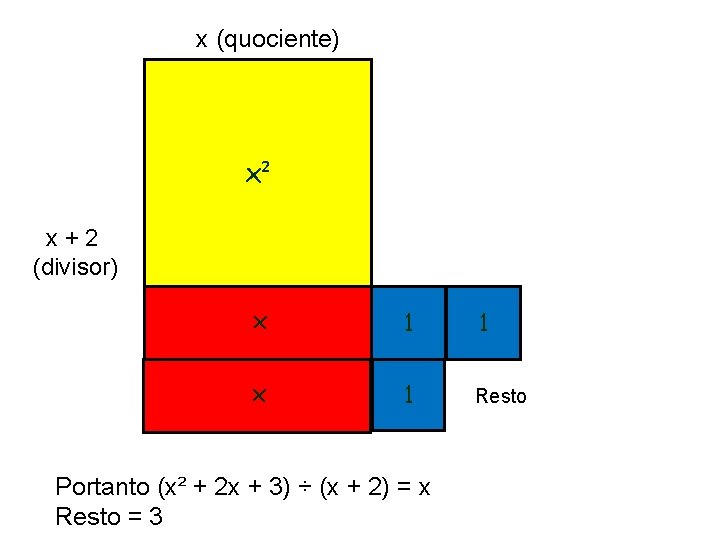
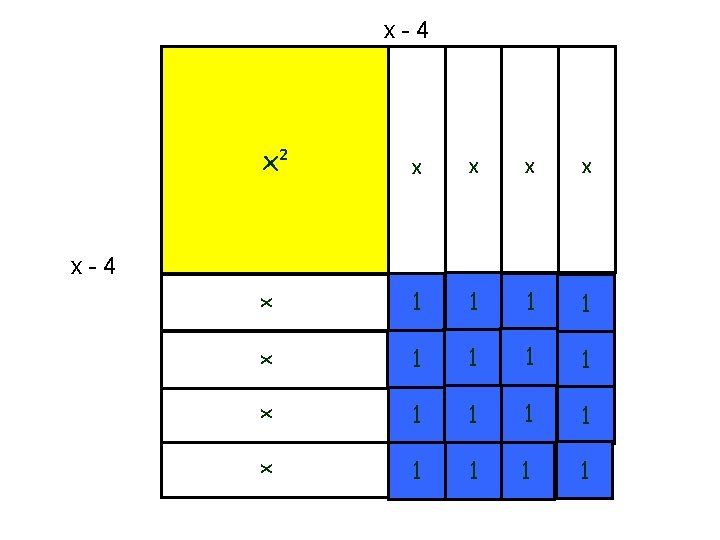
Exemplo 2: Resolva a divisão do polinômio (x² + 2 x + 3) pelo (x + 2) Representando o dividendo com as peças do material

x (quociente) x² x 1 1 x x + 2 (divisor) 1 Resto Portanto (x² + 2 x + 3) ÷ (x + 2) = x Resto = 3

Exemplo 3: Resolva a divisão do polinômio (x² - 3) pelo (x + 2) Representando o dividendo com as peças do material

x – 2 (quociente) x² x x x 1 1 x + 2 (divisor) Portanto (x² - 3) ÷ (x + 2) = x - 2 Resto = 1 1 Resto

Utilizando o material para resolver equações do 2º grau

x + 2 x x x² x 1 x x + 2 1 1 1

x - 4 x x x 1 1 1 1 x x² 1 1 x - 4

x - 3 x x² 1 1 x 1 x x - 2 1

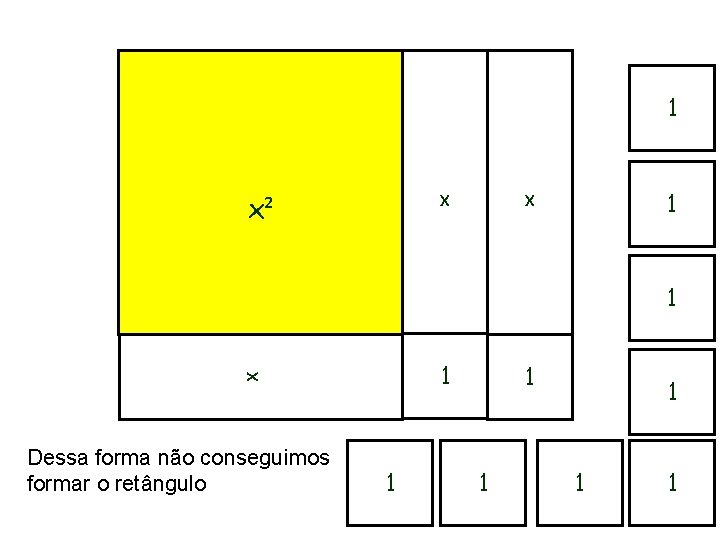
1 1 x x² x 1 Dessa forma não conseguimos formar o retângulo 1 1 1

x x x 1 1 1 1 1 x x²

1 1 1 x x x 1 1 x²

Questão 20ª AAP – 9° Ano Habilidade: Identificar a equação de 2º grau que expressa uma situação problema Questão 1 - Determine a equação de 2º grau, cuja soma de suas raízes é 1 e o produto das raízes é – 12. A) B) C) D) – x² + x - 12 = 0 – x² – x + 12 = 0 x² – x – 12 = 0 x² – x + 12 = 0 Resposta: Alternativa C 49, 04% de acerto - Médio

Itens do Saresp – Relatórios Pedagógicos

H 12 - Realizar operações simples com polinômios. (GII) Nível Diretoria – (Plataforma Foco Aprendizagem 2018 - 50, 51% - etapa 2) Exemplo 1: (Relatório Pedagógico – 2011 – 9º Ano - Adequado) Observe a figura. A expressão que representa o perímetro da figura é A) 5 x + 3. B) 5 x + 1. C) 2 x. D) 5 x – 3.

H 12 - Realizar operações simples com polinômios. (GII) Nível Diretoria – (Plataforma Foco Aprendizagem 2018 - 50, 51% - etapa 2) Exemplo 2: (Relatório Pedagógico – 2009 – 9º Ano - Avançado) Considerando os polinômios A = x – 2, B = 2 x + 1 e C = x, o valor mais simplificado para a expressão A . A - B + C é igual a: (A) x 2 – x – 3 (B) x 2 – x – 5 (C) x 2 – 5 x + 3 (D) x 3 – x 2 – 5 x + 2

H 13 - Simplificar expressões algébricas que envolvam produtos notáveis e fatoração. (GII) Nível Diretoria – (Plataforma Foco Aprendizagem 2018 – 30, 43 % - etapa 2) Exemplo 3: (Relatório Pedagógico – 2015 – 9º Ano - Avançado) A equação (x – 3) · (x – 2) = 0 é a forma fatorada de: A) x 2 – 6 = 0. B) x 2 – 5 x + 6 = 0. C) x 2 + 5 x – 6 = 0. D) 2 x – 5 = 0.

Concluímos que: Utilizar um jogo manipulativo como o Algeplan e, de fato, aprender suas regras, vai acrescentar ao aluno, pois ele estará participando de um novo jogo de linguagem. Mas, devemos perceber que as regras, mesmo semelhantes, não são plausíveis de uma transposição espontânea para a Álgebra. O aluno deverá aprender as regras do Algeplan e também as regras da Álgebra. (POLETO, 2010, p. 55) [. . . ] aprender a seguir as regras impostas no Algeplan não vai tornar desnecessária a aprendizagem das regras da Álgebra para poder participar deste jogo de linguagem. Ou, saber as regras da Álgebra não vai tornar a criança autodidata no Algeplan. (POLETO, 2010, p. 55) Com essa ideia bem organizada, podemos dizer que o trabalho em sala de aula deve se dar basicamente na diversificação dos jogos pelos quais os alunos transitam. Por isso que, como professores, temos que propiciar o trânsito por jogos de linguagem, os mais diversos possíveis. (POLETO, 2010, p. 55)

Referências Avaliação da Aprendizagem em Processo – 2° Bimestre de 2018 (8º, 9º do Ensino Fundamental Anos Finais e 3ª Série do Ensino Médio) BRASIL. Parâmetros Curriculares Nacionais: matemática. Secretaria da Educação Fundamental. Brasília: MEC/SEF, 1997. GRIFFITHS, Rose. A matemática e o brincar. In: MOYLES, Janet R. (Cols) A excelência do brincar. Porto Alegre: Editora Artmed, 1994. PASQUETTI, C. Proposta de aprendizagem de polinômios através de materiais concretos. 2008. 48 f. Trabalho de conclusão de curso (Curso de Matemática - Departamento de Ciências Exatas e da Terra) - Universidade Regional Integrada do Alto Uruguai e das Missões – URI, Erechim – RS, 2008. POLETO, S. C. Algeplan, Álgebra e Geometria: entendendo práticas matemáticas como jogos de linguagem. 2010. 57 f. Trabalho de conclusão de curso (Licenciatura em Matemática) – Universidade Federal do Rio Grande do Sul, Porto Alegre – RS, 2010. São Paulo (Estado) Secretaria da Educação. Currículo do Estado de São Paulo: Matemática e suas tecnologias/Secretaria da Educação; coordenação geral, Maria Inês Fini; coordenação de área, Nilson José Machado. 1 ed. atual. São Paulo: SE, 2012. 72 p. https: //slideplayer. com. br/slide/389996/ (Material elaborado pela Professora Kênia da Silva Souza Furtado - 2009)