Optimization Methods in Energy and Power Systems Lecture

Optimization Methods in Energy and Power Systems Lecture 7: Nonlinear and Mixed-Integer Nonlinear Programming Mahdi Pourakbari Kasmaei, 2019 Thursday, 11 April 2019

Nonlinear & Mixed-Integer Nonlinear Programming ü Introduction of Nonlinear Programming Problems (NLP) ü Formulating NLP Problems ü Introduction of Mixed-Integer NLP (MINLP) ü Formulating MINLP Problems M. Pourakbari Kasmaei, 2019 2

Nonlinear Programming (Introduction) ü Variables are continuous ü The nonlinearity can be a part of: • Objective function • The feasible region that is determined by nonlinear constraint(s). M. Pourakbari Kasmaei, 2019 3

Nonlinear Programming (Introduction) All the representation Forms in LP problems (General, Canonical, and Standard) are also available in NLP problems. M. Pourakbari Kasmaei, 2019 4

an Obj d/ ec m or F tive ig ht eas Fu be ibl nc No e R tion nl eg in io ea n r Formulating NLP Problems (General Form) M. Pourakbari Kasmaei, 2019 5

Nonlinear Programming (NLP) Example 7. 1: Economic Dispatch Cost Coefficient (€/MW) Unit Output (MW) ü In Practice, the cost function is of order 5 or higher. We use Quadratic Cost Function. M. Pourakbari Kasmaei 6

Nonlinear Programming (NLP) Example 7. 1: Economic Dispatch (NLP) M. Pourakbari Kasmaei 7

Nonlinear Programming (NLP) Example 7. 1: Economic Dispatch (NLP) # of Units Generic Formulation of ED M. Pourakbari Kasmaei 8

Nonlinear Programming (NLP) Set i /1*2/; Example Variable z; Positive Variables Pg(i); Equations Eq. Obj, Eq 1, Eq 2, Eq 3, Eq 4, Eq 5; Table gendata(i, *) a b c upplim lowlim 1 0. 0003 10. 1 671 50 0 2 0. 0013 8. 8 374 40 0; 7. 1: Economic Dispatch (NLP) ü ü Set Table Eq. Obj. . z =e= sum(i, gendata(i, 'a')*Power(Pg(i), 2) + gendata(i, 'b')*Pg(i) + gendata(i, 'c')); Eq 1. . sum(i, Pg(i)) =e= 62; Eq 2. . (2/3)*Pg('1') + Pg('2') =l= 68; Eq 3. . 2*Pg('1') + 0. 3*Pg('2') =g= 50; ü NLP Solver Eq 4(i). . Pg(i) =l= gendata(i, 'upplim'); Eq 5(i). . Pg(i) =g= gendata(i, 'lowlim'); Model NLP_ED /ALL/; Solve NLP_ED USING NLP MINIMIZING Z; M. Pourakbari Kasmaei 9

Nonlinear Programming (NLP) Attention ü For nonlinear problems, finding a suitable solver is important. • Although the nonlinearity makes some obstacles in finding the global solution, the main obstacles are related to non-convexity. • Non-convexity results in multiple local optimal solutions. M. Pourakbari Kasmaei 10

Nonlinear Programming (NLP) Example 7. 1: Economic Dispatch (NLP) ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER 1621. 425 +INF 22. 000 40. 000 +INF Solution Using CONOPT MARGINAL. . . ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 ---- EQU Eq 3 ---- EQU Eq 4 1 2 ---- EQU Eq 5 1 2 LOWER 1045. 000 62. 000 -INF 50. 000 LEVEL 1045. 000 62. 000 54. 667 56. 000 UPPER MARGINAL 1045. 000 1. 000 62. 000 10. 113 68. 000. +INF. -INF 22. 000 40. 000 50. 000 40. 000 . -1. 209 . . 22. 000 40. 000 +INF . . M. Pourakbari Kasmaei 11

Nonlinear Programming (NLP) Example 7. 1: Economic Dispatch (NLP) ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER 1621. 425 +INF MARGINAL. 22. 000 40. 000 9. 2833 E-8 EPS +INF Solution Using KNITRO ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 ---- EQU Eq 3 ---- EQU Eq 4 1 2 ---- EQU Eq 5 1 2 M. Pourakbari Kasmaei LOWER 1045. 000 62. 000 -INF 50. 000 LEVEL 1045. 000 62. 000 54. 667 56. 000 UPPER MARGINAL 1045. 000 1. 000 62. 000 10. 113 68. 000 -2. 003 E-7 +INF 8. 0213 E-6 -INF 22. 000 40. 000 50. 000 40. 000 EPS -1. 209 . . 22. 000 40. 000 +INF EPS 12

Nonlinear Programming (NLP) Example 7. 1: Economic Dispatch (NLP) ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER 1621. 425 +INF 22. 000 40. 000 +INF Solution Using LINDO MARGINAL. . . ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 ---- EQU Eq 3 ---- EQU Eq 4 1 2 ---- EQU Eq 5 1 2 M. Pourakbari Kasmaei LOWER 1045. 000 62. 000 -INF 50. 000 LEVEL 1045. 000 62. 000 54. 667 56. 000 UPPER MARGINAL 1045. 000 1. 000 62. 000 10. 113 68. 000. +INF. -INF 22. 000 40. 000 50. 000 40. 000 . . 22. 000 40. 000 +INF 2. 1244 E-8 -1. 209 EPS 13

Nonlinear Programming (NLP) Example 7. 1: Economic Dispatch (NLP) ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER 1621. 425 +INF 22. 000 40. 000 +INF Solution Using LOCALSOLVER Stopped due to time limit (1000 sec) ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 ---- EQU Eq 3 ---- EQU Eq 4 1 2 ---- EQU Eq 5 1 2 M. Pourakbari Kasmaei LOWER 1045. 000 62. 000 -INF 50. 000 LEVEL 1045. 000 62. 000 54. 667 56. 000 UPPER 1045. 000 62. 000 68. 000 +INF -INF 22. 000 40. 000 50. 000 40. 000 . . 22. 000 40. 000 +INF 14

Nonlinear Programming (NLP) It seems that there is No Big Difference among Well-known Solvers! Why? !! M. Pourakbari Kasmaei, 2019 15

Nonlinear Programming (NLP) Example 7. 2: Economic Dispatch (DNLP) Let us consider a non-smooth objective function: ü ED Problem with Valve-point Effect M. Pourakbari Kasmaei 16

Nonlinear Programming (NLP) Ø Discontinuous Nonlinear Program (DNLP) ü Model with Non-smooth Nonlinear terms with Discontinuous Derivatives, Derivatives but no discrete variables ü The same as NLP problems, except that the nonsmooth functions may appear as well. ü These models are more difficult to solve than normal NLP models and it is highly recommended to avoid using such models. M. Pourakbari Kasmaei 17

Nonlinear Programming (NLP) Set i /1*2/; Variable z; Positive Variables Pg(i); Equations Eq. Obj, Eq 1, Eq 2, Eq 3, Eq 4, Eq 5; Table gendata(i, *) a b c e f upplim lowlim 1 0. 0003 10. 1 671 170 0. 091 50 0 2 0. 0013 8. 8 374 110 0. 078 40 0; Eq. Obj. . z =e= sum(i, gendata(i, 'a')*Power(Pg(i), 2) + gendata(i, 'b')*Pg(i) +gendata(i, 'c') +abs(gendata(i, 'e')*sin(gendata(i, 'f')*(gendata(i, 'lowlim')-Pg(i))))); Eq 1. . sum(i, Pg(i)) =e= 62; ü CONOPT Eq 2. . (2/3)*Pg('1') + Pg('2') =l= 68; ü IPOPT Eq 3. . 2*Pg('1') + 0. 3*Pg('2') =g= 50; ü KNITRO Eq 4(i). . Pg(i) =l= gendata(i, 'upplim'); ü SNOPT Eq 5(i). . Pg(i) =g= gendata(i, 'lowlim'); ü …. Option DNLP= NONLINEAR_SOLVER_NAME; Model DNLP_ED /ALL/; Solve DNLP_ED USING DNLP MINIMIZING Z; Example 7. 2: ED (DNLP) M. Pourakbari Kasmaei Set i /1*2/; Variable z; Positive Variables Pg(i); Equations Eq. Obj, Eq 1, Eq 2, Eq 3, Eq 4, Eq 5; Table gendata(i, *) a b c upplim lowlim 1 0. 0003 10. 1 671 50 0 2 0. 0013 8. 8 374 40 0; Eq. Obj. . z =e= sum(i, gendata(i, 'a')*Power(Pg(i), 2) + gendata(i, 'b')*Pg(i) + gendata(i, 'c')); Eq 1. . sum(i, Pg(i)) =e= 62; Eq 2. . (2/3)*Pg('1') + Pg('2') =l= 68; Eq 3. . 2*Pg('1') + 0. 3*Pg('2') =g= 50; Eq 4(i). . Pg(i) =l= gendata(i, 'upplim'); Eq 5(i). . Pg(i) =g= gendata(i, 'lowlim'); Model NLP_ED /ALL/; Solve NLP_ED USING NLP MINIMIZING Z; 18

Nonlinear Programming (NLP) Example 7. 2: Economic Dispatch (NLP) ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER 1912. 872 +INF 50. 000 12. 000 +INF Solution Using CONOPT MARGINAL. . . ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 ---- EQU Eq 3 ---- EQU Eq 4 1 2 ---- EQU Eq 5 1 2 LOWER 1045. 000 62. 000 -INF 50. 000 LEVEL 1045. 000 62. 000 45. 333 103. 600 UPPER MARGINAL 1045. 000 1. 000 62. 000 13. 919 68. 000. +INF. -INF 50. 000 12. 000 50. 000 40. 000 -1. 288. . . 50. 000 12. 000 +INF . . M. Pourakbari Kasmaei 19

Nonlinear Programming (NLP) Example 7. 2: Economic Dispatch (NLP) ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER 1912. 872 +INF 50. 000 12. 000 +INF Solution Using MINOS MARGINAL. . . ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 ---- EQU Eq 3 ---- EQU Eq 4 1 2 ---- EQU Eq 5 1 2 LOWER 1045. 000 62. 000 -INF 50. 000 LEVEL 1045. 000 62. 000 45. 333 103. 600 UPPER MARGINAL 1045. 000 1. 000 62. 000 13. 919 68. 000. +INF. -INF 50. 000 12. 000 50. 000 40. 000 -1. 288. . . 50. 000 12. 000 +INF . . M. Pourakbari Kasmaei 20

Nonlinear Programming (NLP) Example 7. 2: Economic Dispatch (NLP) ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER 1912. 872 +INF 50. 000 12. 000 +INF Solution Using IPOPT MARGINAL. 1. 817 E-11 7. 576 E-11 ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 ---- EQU Eq 3 ---- EQU Eq 4 1 2 ---- EQU Eq 5 1 2 M. Pourakbari Kasmaei LOWER 1045. 000 62. 000 -INF 50. 000 LEVEL 1045. 000 62. 000 45. 333 103. 600 UPPER MARGINAL 1045. 000 1. 000 62. 000 13. 919 68. 000 -4. 01 E-11 +INF 1. 695 E-11 -INF 50. 000 12. 000 50. 000 40. 000 -1. 288 -3. 25 E-11 . . 50. 000 12. 000 +INF 1. 817 E-11 7. 575 E-11 21

Nonlinear Programming (NLP) Example 7. 2: Economic Dispatch (NLP) Failed in Finding the Solution! Solution Using BARON M. Pourakbari Kasmaei 22

Nonlinear Programming (NLP) Example 7. 2: Economic Dispatch (NLP) Failed in Finding the Solution! Solution Using MOSEK M. Pourakbari Kasmaei 23

Nonlinear Programming (NLP) Example 7. 2: Economic Dispatch (NLP) ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER 1778. 239 +INF MARGINAL. 22. 000 40. 000 -6. 78 E-10 EPS +INF Solution Using KNITRO ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 ---- EQU Eq 3 ---- EQU Eq 4 1 2 ---- EQU Eq 5 1 2 M. Pourakbari Kasmaei ---- VAR z ---- VAR Pg 1 2 LOWER 1045. 000 62. 000 -INF 50. 000 LOWER -INF. . LEVEL UPPER MARGINAL 1912. 872 +INF. 50. 000 12. 000 +INF 1. 817 E-11 7. 576 E-11 LEVEL UPPER MARGINAL 1045. 000 1. 000 62. 000 3. 647 54. 667 68. 000 -2. 03 E-10 56. 000 +INF 1. 8410 E-8 -INF 22. 000 40. 000 50. 000 40. 000 EPS -3. 321 . . 22. 000 40. 000 +INF EPS 24

Nonlinear Programming (NLP) Example 7. 2: Economic Dispatch (NLP) ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER 1729. 285 +INF 34. 523 27. 477 +INF MARGINAL. . . Solution Using LINDO/LINDOGLOBAL ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 ---- EQU Eq 3 ---- EQU Eq 4 1 2 ---- EQU Eq 5 1 2 M. Pourakbari Kasmaei ---- VAR z ---- VAR Pg 1 2 LOWER -INF. . LEVEL UPPER MARGINAL 1778. 239 +INF. 22. 000 40. 000 +INF -6. 78 E-10 EPS LOWER 1045. 000 62. 000 -INF 50. 000 LEVEL 1045. 000 62. 000 50. 492 77. 289 UPPER MARGINAL 1045. 000 1. 000 62. 000 4. 224 68. 000. +INF. -INF 34. 523 27. 477 50. 000 40. 000 . . 34. 523 27. 477 +INF . . 25

Nonlinear Programming (NLP) Choosing Proper Solver do Matter! M. Pourakbari Kasmaei, 2019 26

Mixed-Integer NLP (MINLP) ü The nature of problem is Nonlinear. ü At least one Integer Decision Variable Exists. ü Integer variable can be a part of Objective Function and/or the Feasible Region. M. Pourakbari Kasmaei, 2019 27

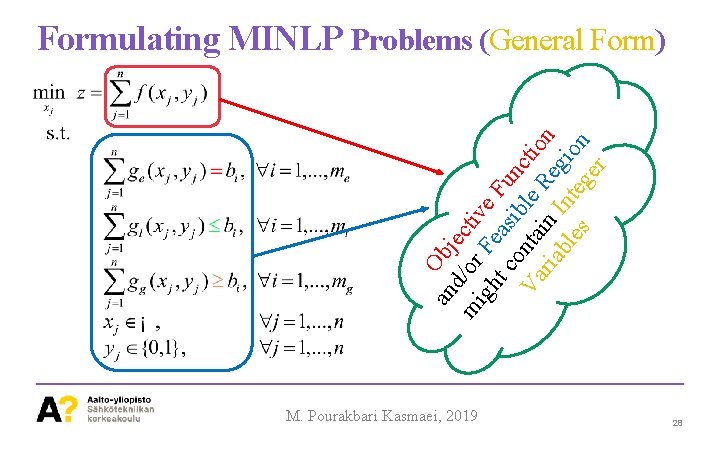
an Obj d e m /or ctiv ig F e h t ea F co sib un Va nta le ctio ria in Re n bl Int gio es eg n er Formulating MINLP Problems (General Form) M. Pourakbari Kasmaei, 2019 28

Mixed-Integer NLP (MINLP) ü Like MILP Problems, we have: • Mixed-Binary NLP (MBNLP) Problem • Integer NLP (INLP) Problems • Binary NLP (BNLP) Problems M. Pourakbari Kasmaei, 2019 29

Mixed-Integer NLP (MINLP) Example 7. 3: Economic Dispatch (MINLP) Cannot Be Handled By Commercial Solvers M. Pourakbari Kasmaei 30

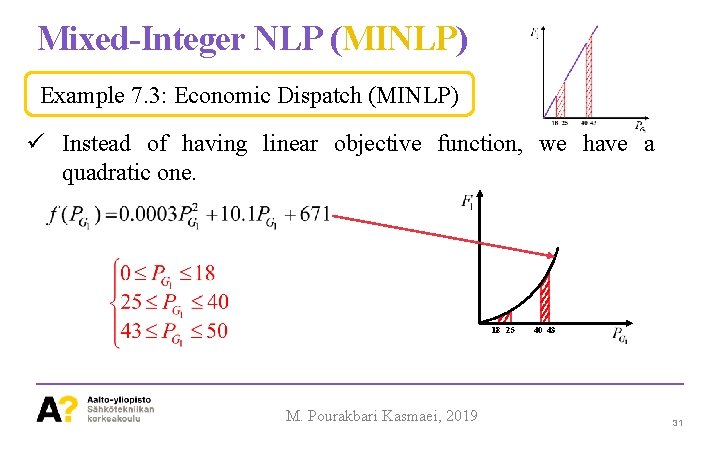
Mixed-Integer NLP (MINLP) Example 7. 3: Economic Dispatch (MINLP) ü Instead of having linear objective function, we have a quadratic one. 18 25 M. Pourakbari Kasmaei, 2019 40 43 31

Mixed-Integer NLP (MINLP) Example 7. 3: Economic Dispatch (MINLP) ü Assign Binary Variables to each Operating Zone 40 43 18 25 Only One Zone should be selected M. Pourakbari Kasmaei, 2019 32

Mixed-Integer NLP (MINLP) Set i /1*2/; Variable z; Positive Variables Pg(i); Equations Eq. Obj, Eq 1, Eq 2, Eq 3, Eq 4_1, Eq 4_2, Eq 4_3, Eq 5; Table gendata(i, *) a b c e f upplim lowlim 1 0. 0003 10. 1 671 170 0. 091 50 0 2 0. 0013 8. 8 374 110 0. 078 40 0; Eq. Obj. . z =e= sum(i, gendata(i, 'a')*Power(Pg(i), 2) + gendata(i, 'b')*Pg(i) +gendata(i, 'c')); Eq 1. . sum(i, Pg(i)) =e= 62; Eq 2. . (2/3)*Pg('1') + Pg('2') =l= 68; Eq 3. . 2*Pg('1') + 0. 3*Pg('2') =g= 50; Eq 4(i). . Pg(i) =l= gendata(i, 'upplim'); Eq 4_1. . Pg('1') =l= 18*u 1 + 40*u 2 + 50*u 3; Eq 4_2. . Pg('1') =g= 25*u 2 + 43*u 3; Eq 4_3. . u 1 + u 2 + u 3 =e= 1; Eq 5(i). . Pg(i) =g= gendata(i, 'lowlim'); Option MINLP= NONLINEAR_SOLVER_NAME; Model MINLP_ED /ALL/; Solve DNLP_ED USING MINLP MINIMIZING Z; Example 7. 3: Economic Dispatch (MINLP) M. Pourakbari Kasmaei 33

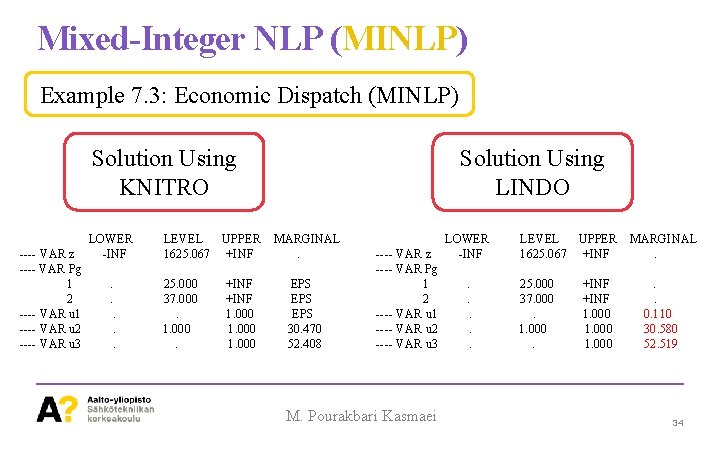
Mixed-Integer NLP (MINLP) Example 7. 3: Economic Dispatch (MINLP) Solution Using KNITRO ---- VAR z ---- VAR Pg 1 2 ---- VAR u 1 ---- VAR u 2 ---- VAR u 3 LOWER -INF. . . LEVEL UPPER 1625. 067 +INF 25. 000 37. 000. 1. 000. +INF 1. 000 Solution Using LINDO MARGINAL. EPS EPS 30. 470 52. 408 ---- VAR z ---- VAR Pg 1 2 ---- VAR u 1 ---- VAR u 2 ---- VAR u 3 M. Pourakbari Kasmaei LOWER -INF. . . LEVEL UPPER 1625. 067 +INF 25. 000 37. 000. 1. 000. +INF 1. 000 MARGINAL. . . 0. 110 30. 580 52. 519 34

Mixed-Integer NLP (MINLP) Example 7. 4: Economic Dispatch (MINLP) Non-smooth Terms M. Pourakbari Kasmaei 35

Mixed-Integer NLP (MINLP) Example 7. 4: Economic Dispatch (MINLP) ü Transform these terms into integer-based terms. 18 25 M. Pourakbari Kasmaei, 2019 40 43 36

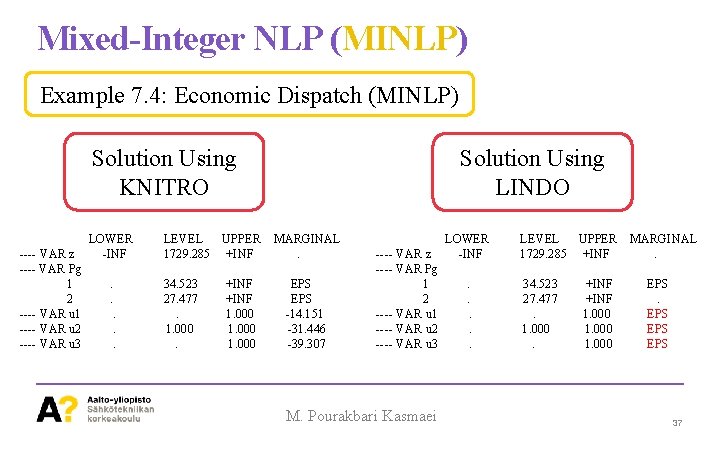
Mixed-Integer NLP (MINLP) Example 7. 4: Economic Dispatch (MINLP) Solution Using KNITRO ---- VAR z ---- VAR Pg 1 2 ---- VAR u 1 ---- VAR u 2 ---- VAR u 3 LOWER -INF. . . LEVEL UPPER 1729. 285 +INF 34. 523 27. 477. 1. 000. +INF 1. 000 Solution Using LINDO MARGINAL. EPS -14. 151 -31. 446 -39. 307 ---- VAR z ---- VAR Pg 1 2 ---- VAR u 1 ---- VAR u 2 ---- VAR u 3 M. Pourakbari Kasmaei LOWER -INF. . . LEVEL UPPER 1729. 285 +INF 34. 523 27. 477. 1. 000. +INF 1. 000 MARGINAL. EPS EPS 37

Some Linearization Techniques Linearization Of Product Terms & SOS 2 Technique M. Pourakbari Kasmaei, 2019 38

Some Linearization Techniques 1) Product of Two Binary Variables M. Pourakbari Kasmaei, 2019 39

Some Linearization Techniques 2) Product of One Binary and One Continuous M. Pourakbari Kasmaei, 2019 40

Some Linearization Techniques 3) Product of Two Continuous Variables M. Pourakbari Kasmaei, 2019 41

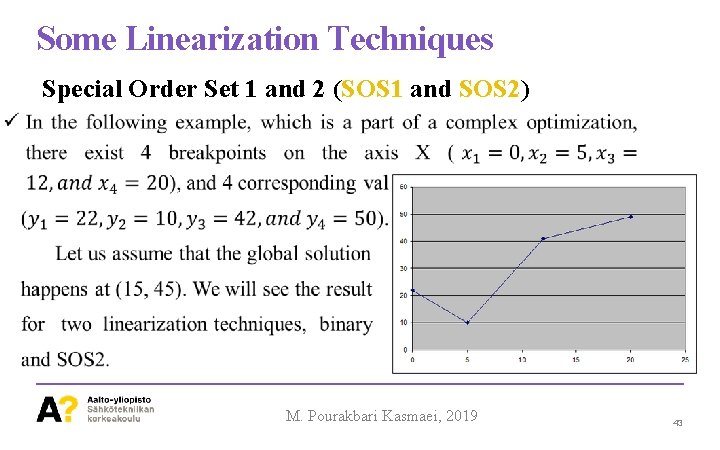
Some Linearization Techniques Special Order Set 1 and 2 (SOS 1 and SOS 2) ü SOS 1 is a set of variables for which at most one variable might be non-zero. ü SOS 2 is a set of variables for which at most two of variables might be non-zero, and if so, these two variables must be adjacent • Therefore, instead of selecting only one breakpoint, two breakpoints are selected and the weighting average of these points is the output. In other words, the value can be between these two breakpoints. M. Pourakbari Kasmaei, 2019 42

Some Linearization Techniques Special Order Set 1 and 2 (SOS 1 and SOS 2) M. Pourakbari Kasmaei, 2019 43

Some Linearization Techniques Special Order Set 1 and 2 (SOS 1 and SOS 2) M. Pourakbari Kasmaei, 2019 44

Some Linearization Techniques Special Order Set 1 and 2 (SOS 1 and SOS 2) M. Pourakbari Kasmaei, 2019 45

Thanks! M. Pourakbari Kasmaei, 2019 46