linear optimization u nonlinear optimization u quadratic optimization



















- Slides: 21



数理最適化問題の種類 線形最適化問題(linear optimization) u 非線形最適化問題(nonlinear optimization) u 二次最適化問題(quadratic optimization) u NP-Hard 整数最適化問題(integer optimization) u 混合整数最適化問題(mixed integer optimization) u




2節 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 線形最適化問題④ from gurobipy import * model = Model ( " lo 1 " ) x 1 = model. add. Var (name="x 1" ) x 2 = model. add. Var (name="x 2" ) x 3 = model. add. Var (ub=30, name="x 3" ) model. update( ) model. add. Constr (2* x 1 + x 2 + x 3 <= 60) model. add. Constr ( x 1 + 2*x 2 + x 3 <= 60) model. set. Objective (15* x 1 + 18* x 2 + 30*x 3 , GRB. MAXIMIZE) model. optimize( ) print "Opt. Value=" , model. Obj. Val for v in model. get. Vars ( ): print v. Var. Name , v. X 実行結果 Opt. Value= 1230. 0 x 1 10. 0 x 2 10. 0 x 3 30. 0




3節 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 整数最適化問題④ from gurobipy import * model = Model ( " seisu " ) x = model. add. Var ( vtype=" I " ) y = model. add. Var ( vtype=" I " ) z = model. add. Var ( vtype=" I " ) model. update ( ) model. add. Constr ( x + y + z == 32) model. add. Constr (2* x + 4*y + 8* z == 80) model. set. Objective ( y + z , GRB. MINIMIZE) model. optimize ( ) print "Opt. Val. =" , model. Obj. Val print " (x , y , z)=" , x. X, y. X, z. X 実行結果 Opt. Val. = 4. 0 (x, y, z)= 28. 0 2. 0



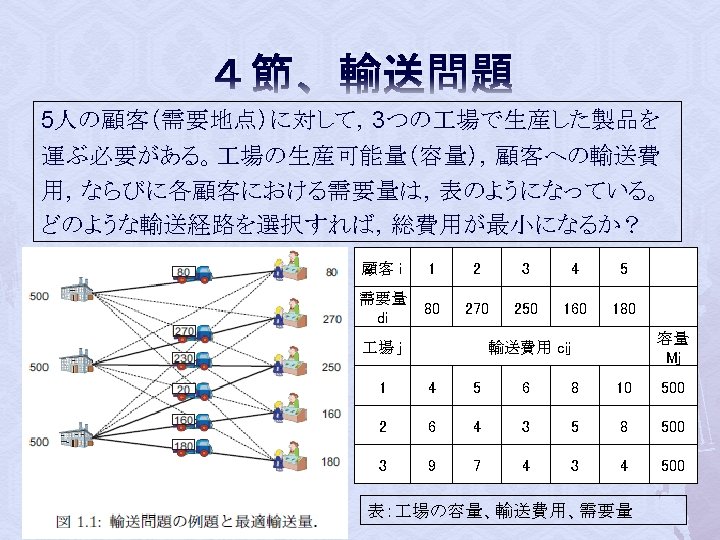
4節 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 輸送問題③ from gurobipy import * d = { 1 : 80 , 2 : 270 , 3: 250 , 4 : 160 , 5: 180} M = { 1 : 500 , 2 : 500 , 3: 500} I=[1, 2, 3, 4, 5] J=[1, 2, 3] I , d = multidict ({ 1 : 80 , 2 : 270 , 3: 250 , 4 : 160 , 5: 180 }) J , M = multidict ({ 1 : 500 , 2 : 500 , 3: 500 } ) c={(1, 1): 4, (1, 2): 6, (1, 3): 9, (2, 1): 5, (2, 2): 4, (2, 3): 7, (3, 1): 6, (3, 2): 3, (3, 3): 4, (4, 1): 8, (4, 2): 5, (4, 3): 3, ( 5 , 1 ) : 10 , ( 5 , 2 ) : 8 , ( 5 , 3 ) : 4 , }

4節 1. 2. 3. 4. 5. 6. 7. 8. 輸送問題④ model = Model ( " transportation " ) x = {} for i in I : for j in J : x [ i , j ] = model. add. Var ( vtype="C" , name="x(%s , %s ) " % ( i , j ) ) model. update ( ) for i in I : model. add. Constr ( quicksum( x [ i , j ] for j in J ) == d [ i ] , ) name="Demand(%s ) " % i 10. for j in J : model. add. Constr ( quicksum( x [ i , j ] for i in I ) <= M [ j ] , name="Capacity(%s ) " % j ) 11. model. set. Objective ( quicksum( c [ i , j ] * x [ i , j ] for ( i , j ) in x ) , GRB. MINIMIZE) 9.

4節 1. 2. 3. 4. 5. 6. 輸送問題⑤ model. optimize ( ) print "Optimal value : " , model. Obj. Val EPS = 1. e-6 for ( i , j ) in x : if x [ i , j ]. X > EPS: print " sending quantity %10 s from factory %3 s to customer %3 s " % ( x [ i , j ]. X, j , i )

4節 輸送問題⑥ 実行結果 Optimal value: 3370. 0 sending quantity 230. 0 from factory 2 to customer 3 sending quantity 20. 0 from factory 3 to customer 3 sending quantity 160. 0 from factory 3 to customer 4 sending quantity 270. 0 from factory 2 to customer 2 sending quantity 80. 0 from factory 1 to customer 1 sending quantity 180. 0 from factory 3 to customer 5



5節 双対問題③ 輸送問題のプログラムの最後に次の文を付け加える。 1. 2. 3. print "Const. Name : Slack , Dual" for c in model. get. Constrs ( ) : print "%s : %s , %s " %(c. Constr. Name , c. Slack , c. Pi )

5節 u u u u u 双対問題④ 実行結果 Const. Name: Slack , Dual Demand(1): 0. 000000 , 4. 000000 Demand(2): 0. 000000 , 5. 000000 Demand(3): 0. 000000 , 4. 000000 Demand(4): 0. 000000 , 3. 000000 Demand(5): 0. 000000 , 4. 000000 Capacity(1): 420. 000000 , 0. 000000 Capacity(2): 0. 000000 , -1. 000000 Capacity(3): 140. 000000 , 0. 000000