Optimization Methods in Energy and Power Systems Lecture

Optimization Methods in Energy and Power Systems Lecture 9: Stochastic Programming Mahdi Pourakbari Kasmaei, 2019 Thursday, 2 May 2019

Stochastic Programming Introduction of Stochastic Programming Stochastic Process Stochastic Programming • Two- and Multi-Stage Problems Quality Metrics M. Pourakbari Kasmaei, 2019 2

Stochastic Programming (Introduction) Decision-making problems in reality are plagued with uncertainty. • In case we have perfect information (the input data are welldefined), the problem is called deterministic, e. g. , all the model and examples in the previous eight lectures. • Decisions need to be made even with lack of perfect information. • Usually, the uncertain data are describable through probability functions. M. Pourakbari Kasmaei, 2019 3

Stochastic Programming (Introduction) • The input data can be presented by a collection of acceptable sets of input data associated with their probabilities of occurrence. Example 9. 1: Perfect Information on Cost Coefficient (Deterministic) Stochastic CC CC Probability (€/MW) 1. 5 0. 2 0. 7 0. 15 2. 0 0. 7 1. 0 0. 73 2. 5 0. 1 1. 2 0. 12 M. Pourakbari Kasmaei, 2019 4

Stochastic Programming (Random Variables) M. Pourakbari Kasmaei, 2019 5

Stochastic Programming (Random Variables) Example 9. 2: Electricity price at noon on a future day is a random variable. • $50/MWh with probability 0. 2 • $46/MWh with probability 0. 6 • $44/MWh with probability 0. 2 M. Pourakbari Kasmaei, 2019 6

Stochastic Programming (Statistical Moments) M. Pourakbari Kasmaei, 2019 7

Stochastic Programming (Statistical Moments) M. Pourakbari Kasmaei, 2019 8

Stochastic Programming (Stochastic Processes) Let us consider two consecutive hours for electricity price. • With perfect information: Hour 12 Hour 13 47 (€/MWh) 49 (€/MWh) M. Pourakbari Kasmaei, 2019 9

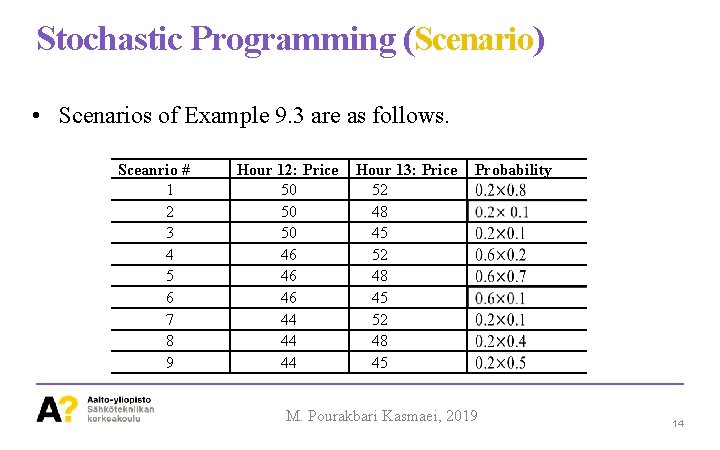
Stochastic Programming (Stochastic Processes) Example 9. 3: Under lack of perfect information, see Ex. 9. 2 for price at noon: Hour 12: Price (Probability) Hour 13: Price (Probability) 50 (0. 2) 46 (0. 6) 44 (0. 2) 52 (0. 8) 48 (0. 1) 45 (0. 1) 52 (0. 2) 48 (0. 7) 45 (0. 1) 52 (0. 1) 48 (0. 4) 45 (0. 5) • These two dependent random variables, price at 12: 00 and price at 13: 00 constitute a stochastic process. M. Pourakbari Kasmaei, 2019 10

Stochastic Programming (Scenario) A convenient manner to characterize stochastic processes is through scenarios. A scenario is a single realization of a stochastic process. Adequate number of scenarios are required to cover the most plausible realizations of the considered stochastic process. M. Pourakbari Kasmaei, 2019 11

Stochastic Programming (Scenario) Adequate Number? ? ? • Considering a small number of scenarios may not capture the important information. • A very large number of scenarios should be generated. • However, this may cause intractablity. M. Pourakbari Kasmaei, 2019 12

Stochastic Programming (Scenario) What To Do? • Large number of scenarios are clustered and the reduced numbers are used as the input scenarios for the stochastic problem. • Scenario reduction methods exist in the literature, and GAMS (scenred, scenred 2) for this purpose. M. Pourakbari Kasmaei, 2019 13

Stochastic Programming (Scenario) • Scenarios of Example 9. 3 are as follows. Sceanrio # 1 2 3 4 5 6 7 8 9 Hour 12: Price 50 50 50 46 46 46 44 44 44 Hour 13: Price 52 48 45 Probability M. Pourakbari Kasmaei, 2019 14

Stochastic Programming (Modelling) Stochastic Programming is used to cope with the uncertainties due to incomplete information in the input data. The decision should be made over a decision horizon that may contain a number of stages. The amount of available information is usually different from one stage to another. • To cover the concept of stage-based stochastic programming we consider the two-stage and multi-stage stochastic programming problems. M. Pourakbari Kasmaei, 2019 15

Stochastic Programming (Two-stage Problems) M. Pourakbari Kasmaei, 2019 16

Stochastic Programming (Two-stage Problems) M. Pourakbari Kasmaei, 2019 17

Stochastic Programming (Two-stage Problems) In Two-Stage Problems we have the following types of decisions: • First-stage or here-and-now decisions. The decisions are made before the realization of the stochastic process. Variables standing for the here-and-now decisions do not depend on each realization of the stochastic process. M. Pourakbari Kasmaei, 2019 18

Stochastic Programming (Two-stage Problems) • Second-stage or wait-and-see decisions. The decisions are made after knowing the actual realization of the stochastic process. Variables standing for the wait-and-see decisions depend on the each realization of the stochastic process. M. Pourakbari Kasmaei, 2019 19

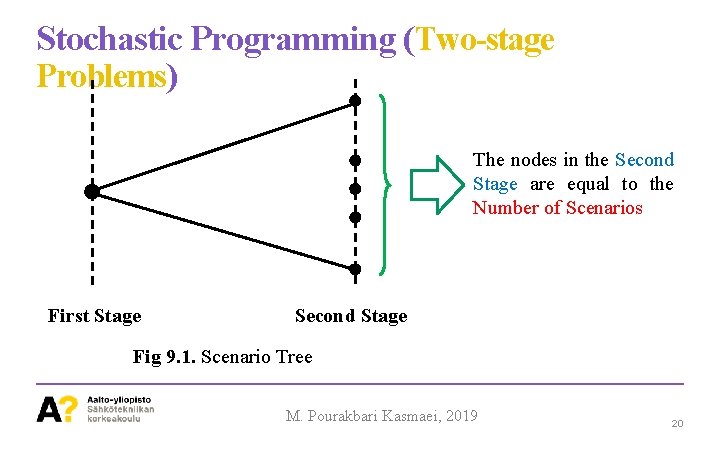
Stochastic Programming (Two-stage Problems) The nodes in the Second Stage are equal to the Number of Scenarios First Stage Second Stage Fig 9. 1. Scenario Tree M. Pourakbari Kasmaei, 2019 20

Stochastic Programming (Two-stage Problems) In a Scenario tree, the branches represent different realizations of the random variables. All these decisions to be optimal, should be derived simultaneously by solving a single optimization problem, so that the relationships among the decision variables are adequately considered. M. Pourakbari Kasmaei, 2019 21

Stochastic Programming (Two-stage Problems General )form of a Two-Stage Linear Programming Problem is as follows. First Stage variable Second Stage variable M. Pourakbari Kasmaei, 2019 22

Stochastic Programming (Two-stage Problems) The Two-Stage model can be equivalently modeled as follows. • This is the deterministic equivalent problem of the stochastic programming problem, presented recently. M. Pourakbari Kasmaei, 2019 23

Stochastic Programming (Two-stage Problems) Stochastic programming problems can be mathematically formulated in two different ways: • Node-variable formulation; the decision variables are associated with decision points. • Scenario-variable formulation; the decision variables are associated with scenarios. M. Pourakbari Kasmaei, 2019 24

Stochastic Programming (Two-stage Problems) Node-variable formulation is more compact than the Scenario-variable formulation, and is particularly well suited for a direct solution approach. Scenario-variable formulation requires a larger number of variables and constraints than the Node-variable formulation but presents an useable structure that is well suited for decomposition. M. Pourakbari Kasmaei, 2019 25

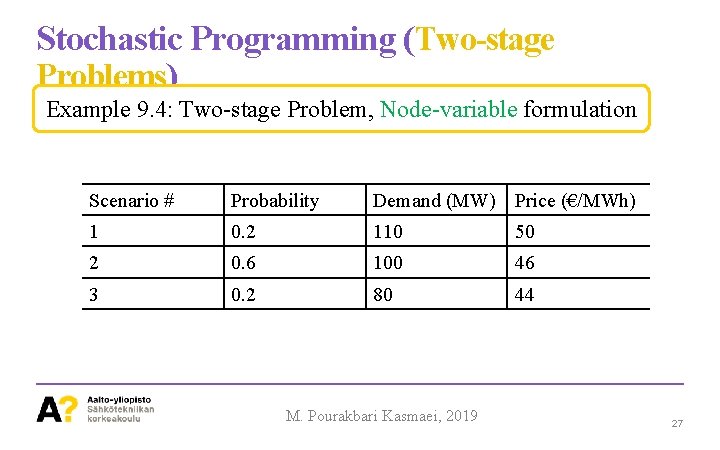
Stochastic Programming (Two-stage Problems ) Example 9. 4: Two-stage Problem, Node-variable formulation A consumer is facing both uncertain electricity demand price for the next week. • Both the price and demand are uncertain but constant throughout the week, see the following Table. • This consumer can buy up to 90 MW at € 45/MWh throughout next week, by signing a bilateral contract before next week, i. e. , before knowing the actual demand pool price. M. Pourakbari Kasmaei, 2019 26

Stochastic Programming (Two-stage Problems) Example 9. 4: Two-stage Problem, Node-variable formulation Scenario # Probability Demand (MW) Price (€/MWh) 1 0. 2 110 50 2 0. 6 100 46 3 0. 2 80 44 M. Pourakbari Kasmaei, 2019 27

Stochastic Programming (Two-stage Problems ) Example 9. 4: Two-stage Problem, Node-variable formulation The problem can be formulated as a two-stage problem. • At the first stage, the consumer has to decide how much to buy from the contract • The second stage make decisions for pool purchases for each of the three realizations (scenarios). M. Pourakbari Kasmaei, 2019 28

Stochastic Programming (Two-stage Problems ) Example 9. 4: Two-stage Problem, Node-variable formulation Bilateral Contract Pool Decisions M. Pourakbari Kasmaei, 2019 29

Stochastic Programming (Two-stage Problems ) Example 9. 4: Two-stage Problem, Node-variable formulation Let us solve it together! M. Pourakbari Kasmaei, 2019 30

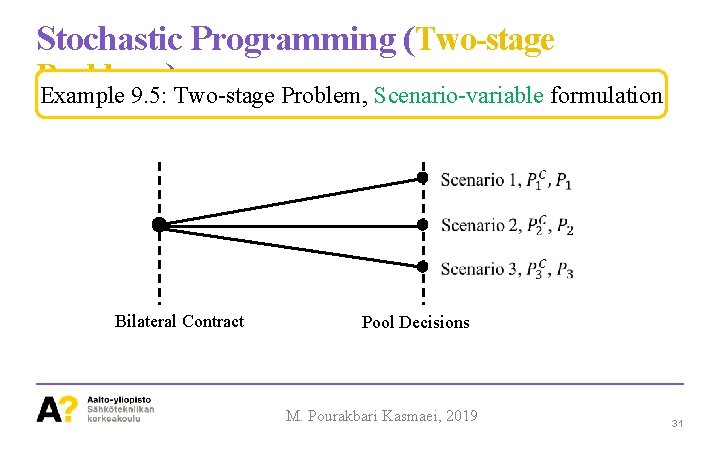
Stochastic Programming (Two-stage Problems ) Example 9. 5: Two-stage Problem, Scenario-variable formulation Bilateral Contract Pool Decisions M. Pourakbari Kasmaei, 2019 31

Stochastic Programming (Two-stage Problems ) Example 9. 5: Two-stage Problem, Scenario-variable formulation Let us solve it together! M. Pourakbari Kasmaei, 2019 32

Thanks! M. Pourakbari Kasmaei, 2019 33