Optimization formulation Optimization methods help us find solutions

Constrained formulation • To avoid a non-smooth function, we can add a bound design

Graphical optimization • Recall the linear constrained optimization formulation. • With only two design

Standard notation • The standard form of an optimization problem used by most textbooks

Column design example • Height is fixed, design variables are D and t. •

Standard dimensionless formulation • Normalized constraints are better both numerically and for communicating degree

Problems • Provide two formulations for minimizing the surface area of a cylinder of

Slides: 10

Download presentation

Optimization formulation • Optimization methods help us find solutions to problems where we seek to find the best of something. • This lecture is about how we formulate the problem mathematically. • In this lecture we make the assumption that we have choices and that we can attach numerical values to the ‘goodness’ of each alternative. • This is not always the case. We may have problems where the only thing we can do is compare pairs of alternatives and tell which one is better, but not by how much. • Can you think of an example?

Young Modulus Example •

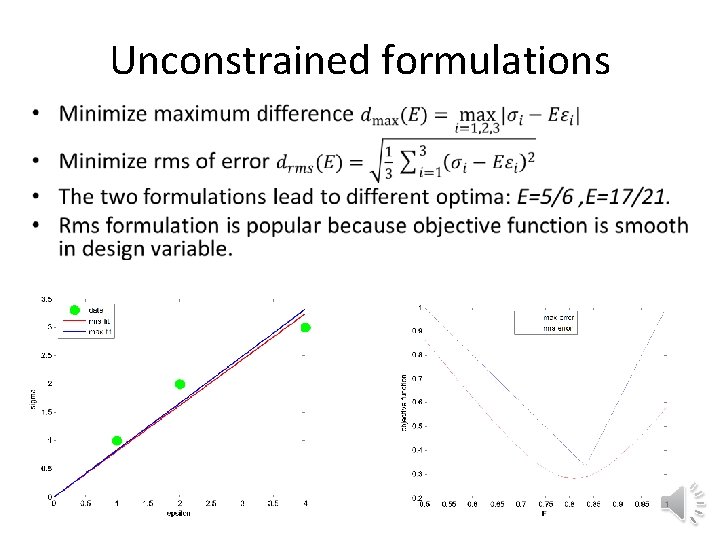
Unconstrained formulations •

Constrained formulation • To avoid a non-smooth function, we can add a bound design variable b, as well as error bounds • The objective function is equal to one design, b, variable. E appears only in the constraints. • Not only is the new objective and constraints smooth, but they are also linear. • Here we know the sign of the differences so we can replace with

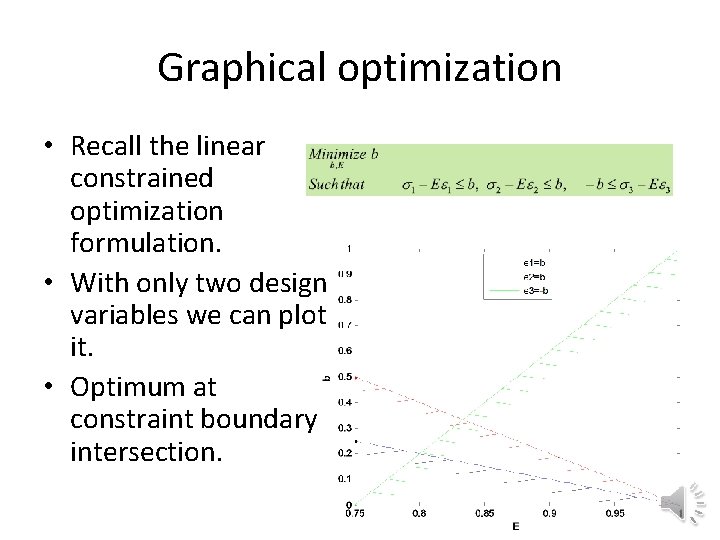
Graphical optimization • Recall the linear constrained optimization formulation. • With only two design variables we can plot it. • Optimum at constraint boundary intersection.

Standard notation • The standard form of an optimization problem used by most textbooks and software is • Standard form of Young’s modulus fit

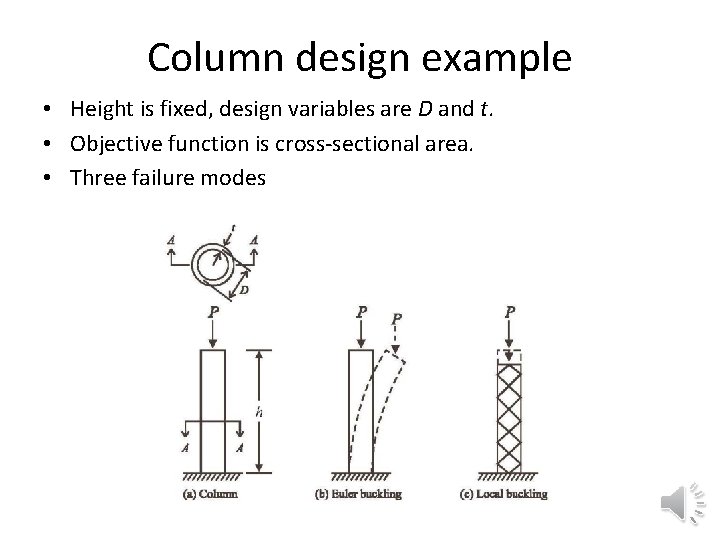
Column design example • Height is fixed, design variables are D and t. • Objective function is cross-sectional area. • Three failure modes

Failure modes •

Standard dimensionless formulation • Normalized constraints are better both numerically and for communicating degree of satisfaction.

Problems • Provide two formulations for minimizing the surface area of a cylinder of a given volume when the diameter and height are the design variables. One formulation should use the volume as equality constraint, and another use it to reduce the number of design variables. • You need to go from point A to point B in minimum time while maintaining a safe distance from point C. Formulate an optimization problem to find the path with no more than three design variables when A=(0, 0), B=(10, 10), C=(4, 4), and the minimum safe distance is 7.