Optimization Methods in Energy and Power Systems Lecture

Optimization Methods in Energy and Power Systems Lecture 2: Solving LP Problems Mahdi Pourakbari Kasmaei, 2019 Thursday, 07 March 2019

Solving LP Problems ü Picturing (Geometric View) ü Algebraically ü Simplex 2

Solving LP Problems (Geometric View) ü Two Main Characteristics • The feasible region, if exists, is always a multidimensional analogue of a polygon. • The objective function is always increasing or decreasing in the same direction, which is perpendicular to the contours. 3

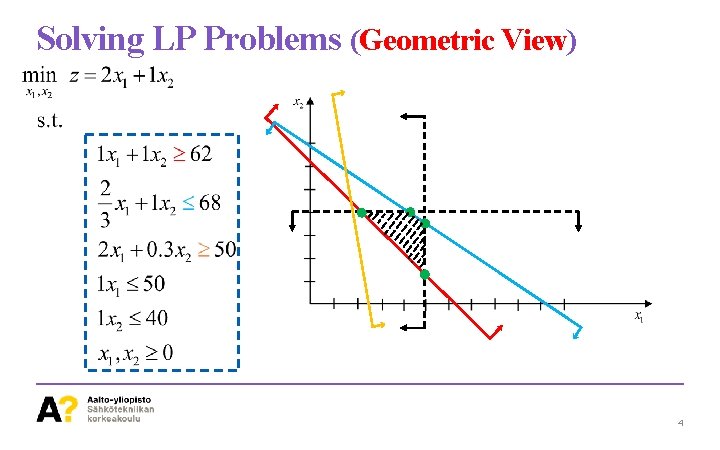
Solving LP Problems (Geometric View) 4

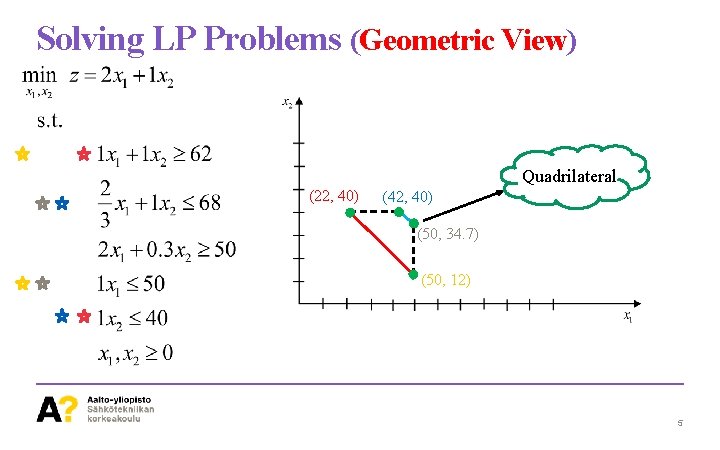
Solving LP Problems (Geometric View) Quadrilateral (22, 40) (42, 40) (50, 34. 7) (50, 12) 5

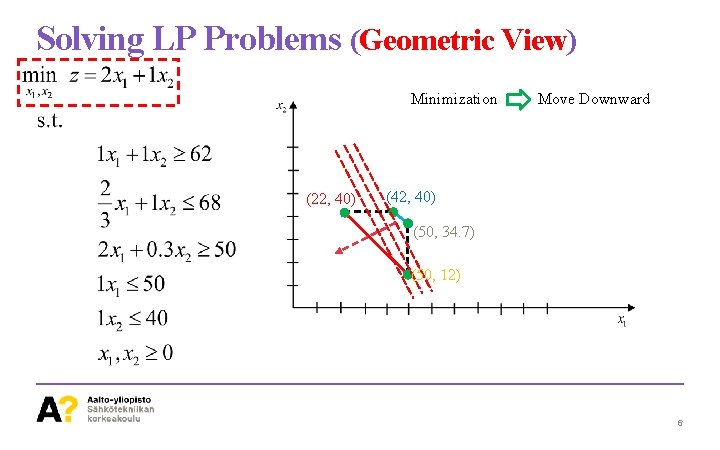
Solving LP Problems (Geometric View) Minimization (22, 40) Move Downward (42, 40) (50, 34. 7) (50, 12) 6

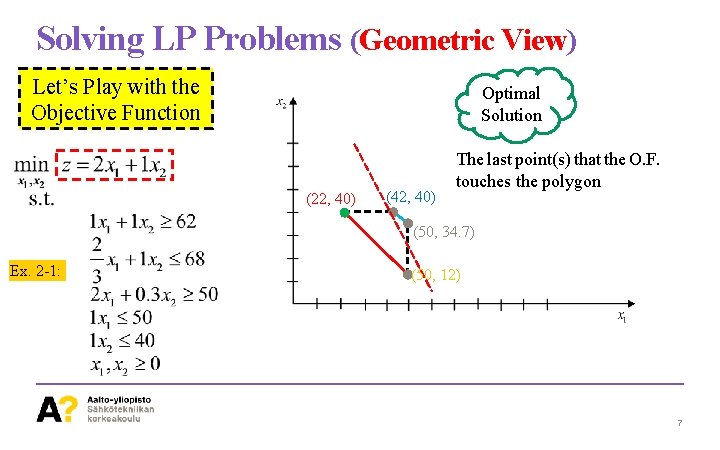
Solving LP Problems (Geometric View) Let’s Play with the Objective Function Optimal Solution (22, 40) (42, 40) The last point(s) that the O. F. touches the polygon (50, 34. 7) Ex. 2 -1: (50, 12) 7

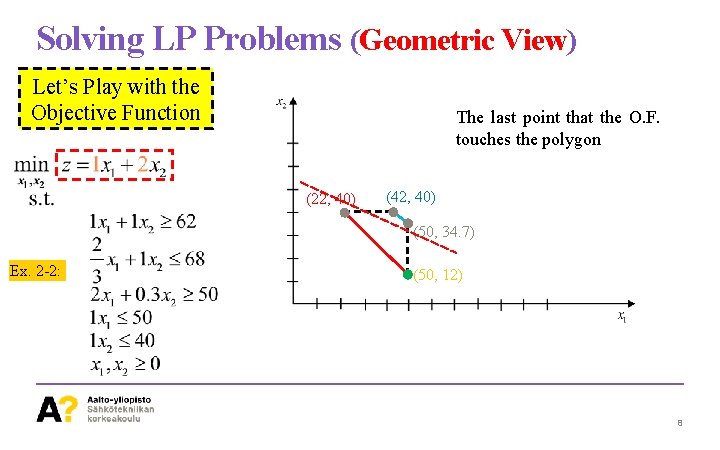
Solving LP Problems (Geometric View) Let’s Play with the Objective Function The last point that the O. F. touches the polygon (22, 40) (42, 40) (50, 34. 7) Ex. 2 -2: (50, 12) 8

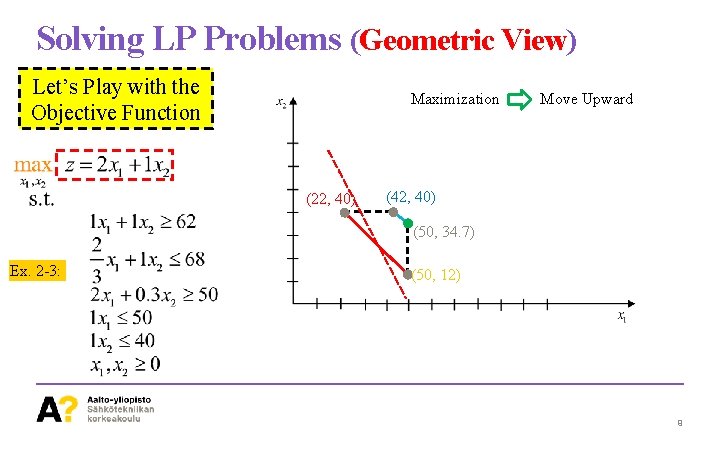
Solving LP Problems (Geometric View) Let’s Play with the Objective Function Maximization (22, 40) Move Upward (42, 40) (50, 34. 7) Ex. 2 -3: (50, 12) 9

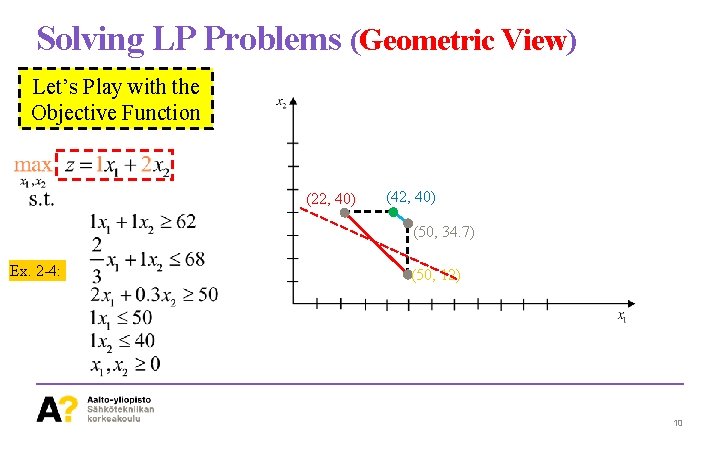
Solving LP Problems (Geometric View) Let’s Play with the Objective Function (22, 40) (42, 40) (50, 34. 7) Ex. 2 -4: (50, 12) 10

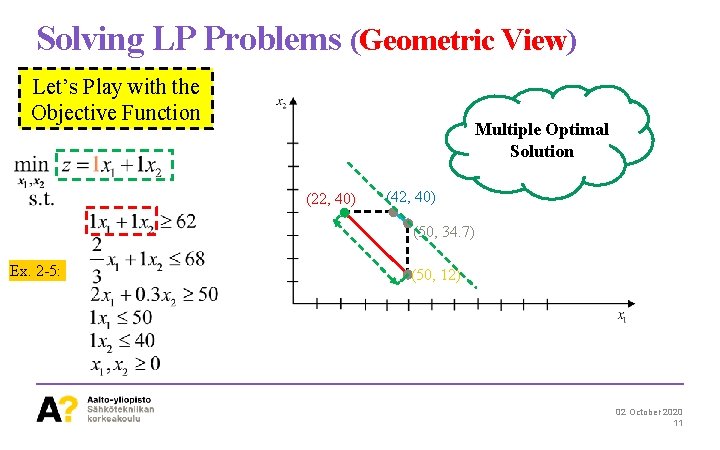
Solving LP Problems (Geometric View) Let’s Play with the Objective Function Multiple Optimal Solution (22, 40) (42, 40) (50, 34. 7) Ex. 2 -5: (50, 12) 02 October 2020 11

Solving LP Problems (Geometric View) (22, 40) (42, 40) (50, 34. 7) (50, 12) ü Vertices or Extreme Points of the Feasible Region are Important; Optimal Solution is one of these points. ü Multiple Optimal Solution occurs if the counter lines of the O. F. are parallel to a side of the polytope. Optimal Solution(s) exist in the Boundary (Point or Line) 12

Solving LP Problems (Class Activity) Together we are Stronger! 13

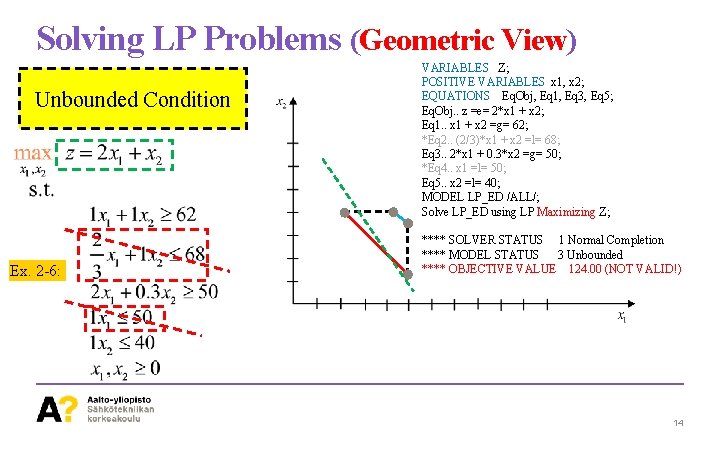
Solving LP Problems (Geometric View) Unbounded Condition Ex. 2 -6: VARIABLES Z; POSITIVE VARIABLES x 1, x 2; EQUATIONS Eq. Obj, Eq 1, Eq 3, Eq 5; Eq. Obj. . z =e= 2*x 1 + x 2; Eq 1. . x 1 + x 2 =g= 62; *Eq 2. . (2/3)*x 1 + x 2 =l= 68; Eq 3. . 2*x 1 + 0. 3*x 2 =g= 50; *Eq 4. . x 1 =l= 50; Eq 5. . x 2 =l= 40; MODEL LP_ED /ALL/; Solve LP_ED using LP Maximizing Z; **** SOLVER STATUS 1 Normal Completion **** MODEL STATUS 3 Unbounded **** OBJECTIVE VALUE 124. 00 (NOT VALID!) 14

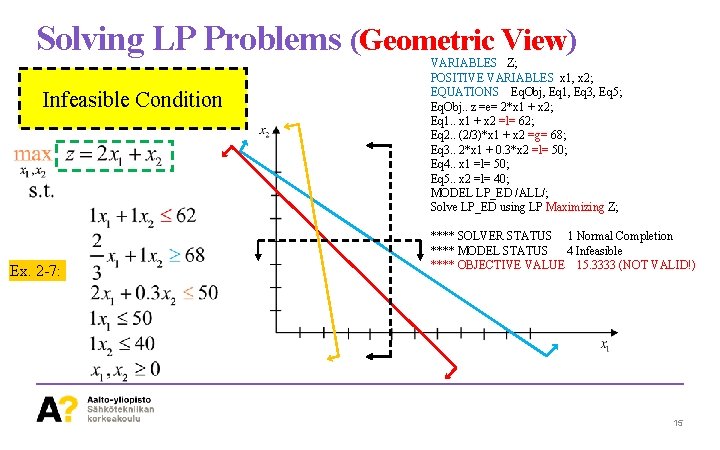
Solving LP Problems (Geometric View) Infeasible Condition Ex. 2 -7: VARIABLES Z; POSITIVE VARIABLES x 1, x 2; EQUATIONS Eq. Obj, Eq 1, Eq 3, Eq 5; Eq. Obj. . z =e= 2*x 1 + x 2; Eq 1. . x 1 + x 2 =l= 62; Eq 2. . (2/3)*x 1 + x 2 =g= 68; Eq 3. . 2*x 1 + 0. 3*x 2 =l= 50; Eq 4. . x 1 =l= 50; Eq 5. . x 2 =l= 40; MODEL LP_ED /ALL/; Solve LP_ED using LP Maximizing Z; **** SOLVER STATUS 1 Normal Completion **** MODEL STATUS 4 Infeasible **** OBJECTIVE VALUE 15. 3333 (NOT VALID!) 15

Solving LP Problems (Algebraically) ü From the Geometric View: • Looking for extreme points is important. ü In Algebraic View: • The extreme points (the intersection of hyperplanes) are found using algebraic techniques. • Determine away to characterize points that may be optimal solutions of an LPP • We need the Standard Form 16

Solving LP Problems (Algebraically) Standard Form 17

Solving LP Problems (Algebraically) Matrix Form 18

Solving LP Problems (Algebraically) Matrix Form 19

Solving LP Problems (Algebraically) We Consider the Equality Constraints (Feasible Region) form algebraic standpoint 7 5 It has more Columns (Variables) than Rows (Equations) 20

Solving LP Problems (Algebraically) ü A way to obtain the solutions is selecting a number of columns equal to the rows. ü Take a way Excess Columns and Assign Zero to the corresponding variables. ü The obtained solutions this way are called Basic Solutions 21

Solving LP Problems (Algebraically) 22

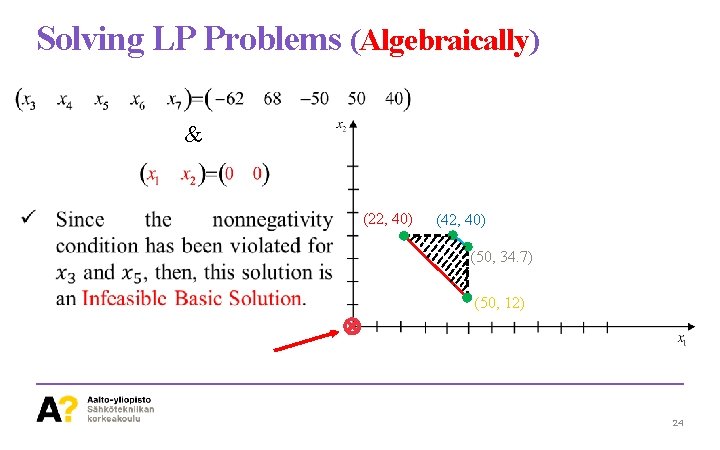
Solving LP Problems (Algebraically) ü Therefore we have, Negative Values!! We have Problem!!!! And after solving: & 23

Solving LP Problems (Algebraically) & (22, 40) (42, 40) (50, 34. 7) (50, 12) 24

Solving LP Problems (Algebraically) 25

Solving LP Problems (Algebraically) ü Therefore we have, And after solving: & 26

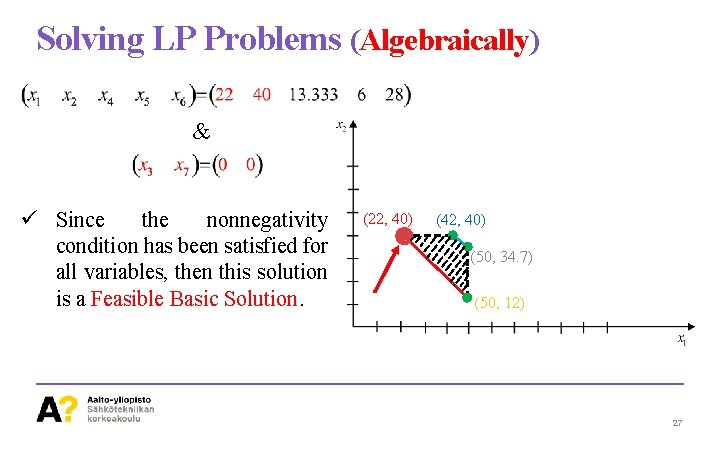
Solving LP Problems (Algebraically) & ü Since the nonnegativity condition has been satisfied for all variables, then this solution is a Feasible Basic Solution. (22, 40) (42, 40) (50, 34. 7) (50, 12) 27

Solving LP Problems (Algebraically) ü Number of combinations of 7 columns taking 5 is 21. ü Now, we will consider the feasible basic solutions. 28

Solving LP Problems (Algebraically) ü The feasible basic solutions are as follows. & & 29

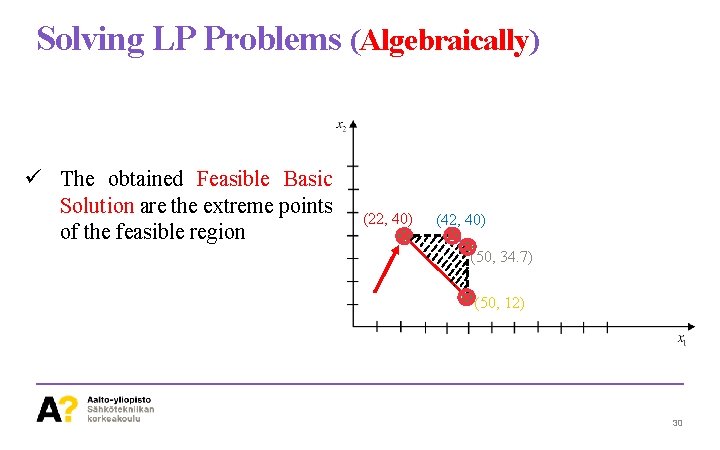
Solving LP Problems (Algebraically) ü The obtained Feasible Basic Solution are the extreme points of the feasible region (22, 40) (42, 40) (50, 34. 7) (50, 12) 30

Concluding Remarks ü In Geometrical Method, each Extreme Point of the feasible region is a Basic Feasible Solution of the Algebraic method; In Geometric viewpoint, General Form can be used, while in Algebraic viewpoint, Standard Form is used. Minimization Problem ü If an LP problem has a solution, this solution is one of the Extreme Points (Basic Feasible Solution). 31

Concluding Remarks ü Therefore, we may use the Geometric Viewpoint to find all the Extreme Points, however, this is good for systems with two decision variables. ü Another possible strategy is checking all Basic Feasible Solutions which may take too much time. ü An alternative solution strategy is to find a Basic Feasible Solution and then jump to another Basic Feasible Solution while decreasing the objective function until no further decrease is possible. This is the Simplex Algorithm. 32

Thanks! 33