Optimization Methods in Energy and Power Systems Lecture

Optimization Methods in Energy and Power Systems Lecture 5: Duality & Bilevel Programming Mahdi Pourakbari Kasmaei, 2019 Thursday, 28 March 2019

Linear Programming ü Duality Properties • Weak Duality • Strong Duality ü Bilevel Programming • Introduction • Application & Formulation 2

LP Problems (Duality in General Form) Constraints Variabes (Min Problem) (Max Problem) Variabes Constraints ü Previously on Duality… 3

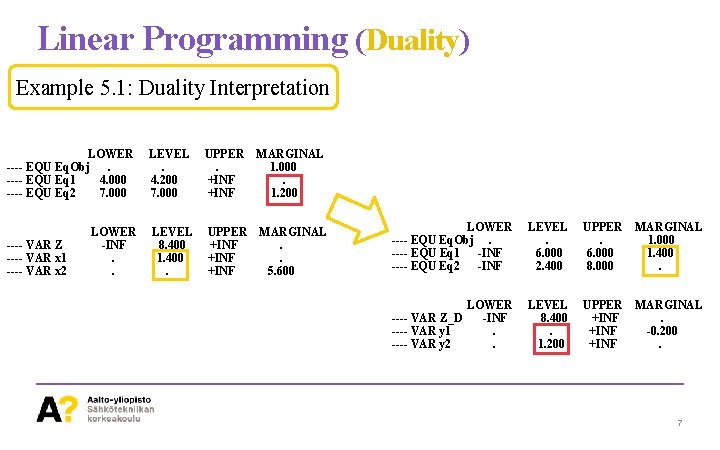
Linear Programming (Duality) Example 5. 1: Duality Interpretation 4

Linear Programming (Duality) Example 5. 1: Duality Interpretation Variables Z_P; Positive Variables x 1, x 2; Equations Eq. Obj, Eq 1, Eq 2; Eq. Obj. . z =e= 6*x 1 + 8*x 2; Eq 1. . 3*x 1 + x 2 =g= 4; Eq 2. . 5*x 1 + 2*x 2 =g= 7; Shadow Price Model LP_ED /ALL/; Solve LP_ED using LP Minimizing Z_P; Dual Variable ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 LOWER. 4. 000 7. 000 LEVEL. 4. 200 7. 000 UPPER. +INF MARGINAL 1. 000. 1. 200 ---- VAR Z ---- VAR x 1 ---- VAR x 2 LOWER -INF. . LEVEL 8. 400 1. 400. UPPER +INF MARGINAL. . 5. 600 5

Linear Programming (Duality) Example 5. 1: Duality Interpretation Variables Z_D; Positive Variables y 1, y 2; Equations Eq. Obj, Eq 1, Eq 2; Eq. Obj. . z =e= 4*y 1 + 7*y 2; Eq 1. . 3*y 1 + 5*y 2 =l= 6; Eq 2. . 1*y 1 + 2*y 2 =l= 8; Shadow Price Model LP_ED /ALL/; Solve LP_ED using LP Maximizing Z_D; ---- EQU Eq. Obj ---- EQU Eq 1 ---- EQU Eq 2 LOWER. -INF LEVEL. 6. 000 2. 400 UPPER. 6. 000 8. 000 MARGINAL 1. 000 1. 400. ---- VAR Z_D ---- VAR y 1 ---- VAR y 2 LOWER -INF. . LEVEL 8. 400. 1. 200 UPPER +INF MARGINAL. -0. 200. 6

Linear Programming (Duality) Example 5. 1: Duality Interpretation LOWER ---- EQU Eq. Obj. ---- EQU Eq 1 4. 000 ---- EQU Eq 2 7. 000 LEVEL. 4. 200 7. 000 UPPER. +INF MARGINAL 1. 000. 1. 200 LOWER -INF. . LEVEL 8. 400 1. 400. UPPER +INF MARGINAL. . 5. 600 ---- VAR Z ---- VAR x 1 ---- VAR x 2 LOWER ---- EQU Eq. Obj. ---- EQU Eq 1 -INF ---- EQU Eq 2 -INF LEVEL. 6. 000 2. 400 UPPER. 6. 000 8. 000 MARGINAL 1. 000 1. 400. LOWER -INF. . LEVEL 8. 400. 1. 200 UPPER +INF MARGINAL. -0. 200. ---- VAR Z_D ---- VAR y 1 ---- VAR y 2 7

Linear Programming (Duality) ü Shadow Prices are Equivalent to the values of Dual Variables. ü Dual Variables of Dual Problem are Equivalent to the Primal Variables. 8

Linear Programming (Duality) Weak Duality Inequality & Strong Duality Equality 9

Linear Programming (Weak Duality) • If the Primal is Min Problem: • And the Dual is Max Problem: Weak Duality Inequality ü Therefore, if x, and y are feasible in the primal and dual problems, , we have: 10

Linear Programming (Weak Duality) ü The Weak-duality property says that the objectivefunction value corresponds to any feasible point in the Dual Problem provides a bound on the objectivefunction value of any feasible point in the Primal Problem and vice versa. (1) 11

Linear Programming (Duality Gap) Duality Gap ü For a pair of feasible solutions The difference: Is called the Duality Gap 12

Linear Programming (Weak Duality) Ø Weak-duality property applies to any Form of primal problem and its dual (Canonical, Standard, etc. ). Ø Depending on the directions of the inequalities, signs of the variables, and Max/Min objective in the Primal and Dual, the direction of the inequality (1) may change. Ø To apply the weak-duality property, it is beneficial to convert the primal problem into Canonical Form. 13

Linear Programming (Strong Duality) • If the Primal is Min Problem: • And the Dual is Max Problem: Strong Duality Equality 14

Linear Programming (Strong Duality) • Strong Duality is the binding condition of the Weak Duality Inequality and states that the Duality Gap for the pairs of Optimal Solution is Zero. 15

LP Problems (Bilevel Programming) Bilevel Programming 16

LP Problems (Bilevel Programming) Ø Bilevel Programmig? • An Optimization Problem that contains another Optimization Problem in the Constraints. • Lower level actions depend on upper level decisions. • The Upper-level problem is called Leader, and the Lower-level problem is called Follower. 17

LP Problems (Bilevel Programming) Ø General Optimization Problem • One Objective Function, and a Set of Constraints 18

LP Problems (Bilevel Programming) Ø Multiobjective Optimization Problem • More than One Objective Function, and a Set of Constraints for both of them. 19

LP Problems (Bilevel Programming) Ø Multiobjective Optimization Problem • Usually can be seen in the following representation 20

LP Problems (Bilevel Programming) Ø Bilevel Optimization Problem • An Optimization Problem that contains another Optimization Problem in the Constraints. Upper Level Lower Level 21

LP Problems (Bilevel Programming) Ø Applications, to name but a few • Transportation (taxation, network design, trip demand estimation) • Management (coordination of multidivisional firms, network facility location, credit allocation), • Planning (agricultural policies, electric utility). • Market 22

LP Problems (Bilevel Programming) Ø Key Concept in Game Theory ü Situations involving more than one decision-maker (player). ü Leads to the notion of conflict or competition. 23

LP Problems (Bilevel Programming) Ø Two Objective Function in One Optimization Problem? ? ? ! We’ve got a Problem!!!! 24

LP Problems (Bilevel Programming) 25

LP Problems (Bilevel Programming) Ø How to solve Bilevel Problem • Strong Duality Property: ü Step 1: Find the Dual of the lower level ü Step 2: Apply the Strong Duality Property (Condition) ü Step 3: Consider all the Constraints of Primal and Dual models of the Lower Level problem and the Strong Duality Condition together ü Step 4: Consider equations obtained in Step 3 as a set of new Constraint for the Upper Level problem. 26

LP Problems (Bilevel Programming) Ø Step 1: Let us first work on the Lower Level, for the sake of clarity, we add new indices P and D (stand for Primal and Dual, respectively); Find its Dual as: 27

LP Problems (Bilevel Programming) Ø Step 2: We will use the Strong Duality Condition Ø One star ”*” term stand for the optimal solution of the Upper level Problem, while double-star ”**” terms are the optimal solutions of the Primal and Dual Model of the lower level problem. 28

LP Problems (Bilevel Programming) Ø Step 3: The constraints of primal and dual of the lower level, and the strong duality condition are considered. Ø As can be seen, there is no objective for this problem. Note that the double-star terms ”**” are decision-making variables here. 29

LP Problems (Bilevel Programming) Ø Step 4: now, let’s consider these constraints as a new set of constraints for the upper level. Ø Note that, after finding the equivalent single-level model, all the Parameters with ”*” turns into variables. 30

LP Problems (Bilevel Programming) Example 5. 2: Bilevel Programming 31

LP Problems (Bilevel Programming) Example 5. 1: Step 1: find the dual of LL problem 32

LP Problems (Bilevel Programming) Example 5. 2: Step 2: Consider the strong duality Condition 33

LP Problems (Bilevel Programming) Example 5. 2: Step 3: Consider all the Constraints of Primal and Dual models of the Lower Level problem and the Strong Duality Condition together 34

LP Problems (Bilevel Programming) Example 5. 2: Step 4: Find the single-level equivalent 35

Thanks! 36