On Homomorphic Encryption and Secure Computation challenge response

On Homomorphic Encryption and Secure Computation challenge response Shai Halevi June 16, 2011

Computing on Encrypted Data Wouldn’t it be nice to be able to… o Encrypt my data in the cloud o While still allowing the cloud to search/sort/edit/… this data on my behalf o Keeping the data in the cloud in encrypted form Ø Without needing to ship it back and forth to be decrypted June 16, 2011 2

Computing on Encrypted Data Wouldn’t it be nice to be able to… o Encrypt my queries to the cloud o While still allowing the cloud to process them o Cloud returns encrypted answers Ø that I can decrypt June 16, 2011 3

Computing on Encrypted Data Directions • From: Tel-Aviv University, Tel-Aviv, Israel • To: Technion, Haifa, Israel June 16, 2011 $skj#h. S 28 ksyt. A@ … 4

Computing on Encrypted Data $kjh 9*mslt@na 0 &ma. Xxjq 02 bflx m^00 a 2 nm 5, A 4. p. E. abxp 3 m 58 bsa (3 sa. M%w, snanba nq~m. D=3 akm 2, A Z, ltnhde 83|3 mz{n dewiunb 4]gnb. Ta* kjew^bw. J^mdns 0 June 16, 2011 5

Constructing Homomorphic Encryption

Privacy Homomorphisms [RAD 78] Plaintext space P x 1 x 2 ci Enc(xi) Ciphertext space C c 1 * y c 2 # y Dec(d) d Some examples: o “Raw RSA”: c xe mod N (x cd mod N) Ø x 1 e x x 2 e = (x 1 x x 2)e mod N o GM 84: Enc(0) R QR, Enc(1) R QNR (in ZN*) Ø Enc(x 1) x Enc(x 2) = Enc(x 1 x 2) mod N June 16, 2011 7

More Privacy Homomorphisms o Mult-mod-p [El. Gamal’ 84] o Add-mod-N [Pallier’ 98] o Quadratic-polys mod p [BGN’ 06] o Branching programs [IP’ 07] o Later, a “different type of solution” for any circuit [Yao’ 82, …] ØAlso NC 1 circuits [SYY’ 00] June 16, 2011 8

(x, +)-Homomorphic Encryption It will be really nice to have… o Plaintext space Z 2 (w/ ops +, x) o Ciphertexts live in an algebraic ring R (w/ ops +, x) o Homomorphic for both + and x Ø Enc(x 1) + Enc(x 2) in R = Enc(x 1+ x 2 mod 2) Ø Enc(x 1) x Enc(x 2) in R = Enc(x 1 x x 2 mod 2) o Then we can compute any function on the encryptions Ø Since every binary function is a polynomial o We won’t get exactly this, but it’s a good motivation June 16, 2011 9

Some Notations o An encryption scheme: (Key. Gen, Enc, Dec) ØPlaintext-space = {0, 1} Ø(pk, sk) Key. Gen($), c Encpk(b), b Decsk(c) o Semantic security [GM’ 84]: (pk, Encpk(0)) (pk, Encpk(1)) means indistinguishable by efficient algorithms June 16, 2011 10

Homomorphic Encryption o H = {Key. Gen, Enc, Dec, Eval} c* Evalpk(f, c) c* o Homomorphic: Decsk(Evalpk( f, Encpk(x))) = f(x) Ø c* may not look like a “fresh” ciphertext Ø As long as it decrypts to f(x) o Function-private: c* hides f o Compact: Decrypting c* easier than computing f Ø |c*| independent of the complexity of f June 16, 2011 11

(x, +)-Homomorphic Encryption, the [Gentry 09] blueprint Evaluate any function in four “easy” steps o Step 1: Encryption from linear ECCs Ø Additive homomorphism o Step 2: ECC lives inside a ring Ø Also multiplicative homomorphism Ø But only for a few operations (i. e. , low-degree poly’s) o Step 3: Bootstrapping Ø Few ops (but not too few) any number of ops o Step 4: Everything else June 16, 2011 12

Step One: Encryption from Linear ECCs o For “random looking” codes, hard to distinguish close/far from code o Many cryptosystems built on this hardness ØE. g. , [Mc. Eliece’ 78, AD’ 97, GGH’ 97, R’ 03, …] June 16, 2011 13

Encryption from linear ECCs o Key. Gen: choose a “random” code C ØSecret key: “good representation” of C § Allows correction of “large” errors ØPublic key: “bad representation” of C o Enc(0): a word close to C o Enc(1): a random word ØFar from C (with high probability) June 16, 2011 14

An Example: Integers mod p (similar to [Regev’ 03]) p N o Code determined by an integer p ØCodewords: multiples of p o Good representation: p itself o Bad representation: ri << p ØN = pq, and also many xi = pqi + ri o Enc(0): subset-sum(xi’s)+r mod N o Enc(1): random integer mod N June 16, 2011 15

A Different Input Encoding o Both Enc(0), Enc(1) close to the code ØEnc(0): distance to code is even ØEnc(1): distance to code is odd o In our example of integers mod p: ØEnc(b) = 2(subset-sum(xi’s)+r) +b mod N ØDec(c) = (c mod p) mod 2 June 16, 2011 16

Additive Homomorphism o c 1+c 2 = (codeword 1+codeword 2) +2(r 1+r 2)+b 1+b 2 Øcodeword 1+codeword 2 Code ØIf 2(r 1+r 2)+b 1+b 2 < min-dist/2, then it is the dist(c 1+c 2, Code) = 2(r 1+r 2)+b 1+b 2 dist(c 1+c 2, Code) mod 2 = b 1+b 2 o Additively-homomorphic while close to Code June 16, 2011 17

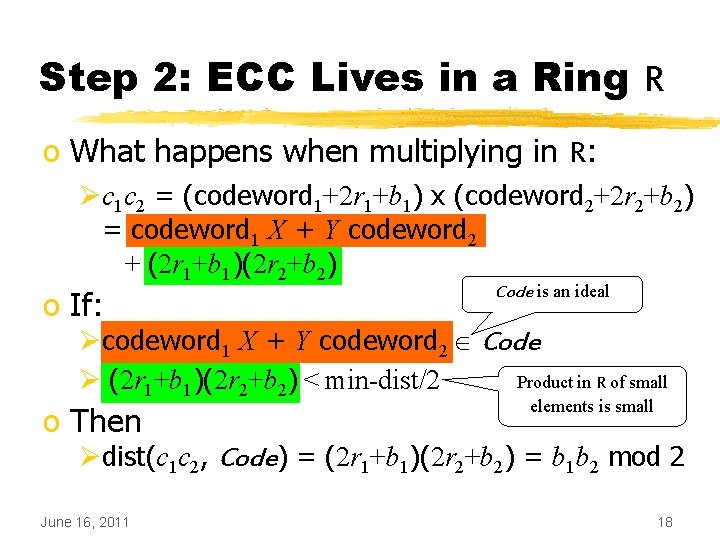
Step 2: ECC Lives in a Ring R o What happens when multiplying in R: Øc 1 c 2 = (codeword 1+2 r 1+b 1) x (codeword 2+2 r 2+b 2) = codeword 1 X + Y codeword 2 + (2 r 1+b 1)(2 r 2+b 2) o If: Code is an ideal Øcodeword 1 X + Y codeword 2 Code Product in R of small Ø (2 r 1+b 1)(2 r 2+b 2) < min-dist/2 o Then elements is small Ødist(c 1 c 2, Code) = (2 r 1+b 1)(2 r 2+b 2) = b 1 b 2 mod 2 June 16, 2011 18

Instantiations o [Gentry ‘ 09] Polynomial Rings Ø Security based on hardness of “Bounded-Distance Decoding” in ideal lattices o [v. DGHV ‘ 10] Integer Ring Ø Security based on hardness of the “approximate. GCD” problem o [GHV ‘ 10] Matrix Rings* Ø Only degree-2 polynomials, security based on hardness of “Learning with Errors” o [BV ‘ 11 a] Polynomial Rings Ø Security based on “ring LWE” June 16, 2011 19

Step 3: Bootstrapping [G’ 09] o So far, can evaluate low-degree polynomials x 1 x 2 … P P(x 1, x 2 , …, xt) xt June 16, 2011 26

Step 3: Bootstrapping [G’ 09] o So far, can evaluate low-degree polynomials x 1 x 2 … P P(x 1, x 2 , …, xt) xt o Can eval y=P(x 1, x 2…, xn) when xi’s are “fresh” o But y is an “evaluated ciphertext” ØCan still be decrypted ØBut eval Q(y) will increase noise too much June 16, 2011 27

Step 3: Bootstrapping [G’ 09] o So far, can evaluate low-degree polynomials x 1 x 2 … P P(x 1, x 2 , …, xt) xt o Bootstrapping to handle higher degrees: o For ciphertext c, consider Dc(sk) = Decsk(c) ØHope: Dc(*) is a low-degree polynomial in sk ØThen so are Ac 1, c 2(sk) = Decsk(c 1) + Decsk(c 2) and Mc 1, c 2(sk) = Decsk(c 1) x Decsk(c 2) June 16, 2011 28

Step 3: Bootstrapping [G’ 09] o Include in the public key also Encpk(sk) x 1 c 1 sk 2 … skn June 16, 2011 x 2 c 2 Requires “circular security” Mc 1, c 2 c Mc 1, c 2(sk) = Decsk(c 1) x Decsk(c 2) = x 1 x x 2 29

Step 3: Bootstrapping [G’ 09] o Include in the public key also Encpk(sk) x 1 c 1 sk 2 … skn x 2 c 2 Requires “circular security” Mc 1, c 2 c Mc 1, c 2(sk) = Decsk(c 1) x Decsk(c 2) = x 1 x x 2 o Homomorphic computation applied only to the “fresh” encryption of sk June 16, 2011 30

Step 4: Everything Else o Cryptosystems from [G’ 09, v. DGHV’ 10, BG’ 11 a] cannot handle their own decryption o Tricks to “squash” the decryption procedure, making it low-degree June 16, 2011 31

Performance o Evaluating only low-degree polynomials may be reasonable o But bootstrapping is inherently inefficient ØHomomorphic decryption for each multiplication o Best implementation so far is [GH’ 11 a] ØPublic key size ~ 2 GB ØEvaluating a multiplication takes 30 minutes June 16, 2011 32

Beyond the [G’ 09] Blueprint o [GH’ 11 b] no “squashing”, still very inefficient o [BV’ 11 b] no underlying ring, only vectors ØAlso no “squashing”, but still inefficient o [G’ 11] no bootstrapping ØBuilds heavily on [BV’ 11 b] ØReduces noise “cheaply” after each multiplication ØShould be at least 2 -3 orders of magnitude better than [GV’ 11 a] June 16, 2011 33

Homomorphic Encryption vs. Secure Computation

Secure Function Evaluation (SFE) Client Alice has data x Server Bob has function f Alice wants to learn f(x) 1. Without telling Bob what x is 2. Bob may not want Alice to know f 3. Client Alice may also want server Bob to do most of the work computing f(x) June 16, 2011 35

Two-Message SFE [Yao’ 82, …] Alice(x) (c, s) SFE 1(x) y SFE 3(s, r) Bob(f) c r r SFE 2(f, c) o Many different instantiations are available Ø Based on hardness of factoring/DL/lattices/… o Alice’s x and Bob’s f are kept private o But Alice does as much work as Bob Ø Bob’s reply of size poly(n) x (|f|+|x|) June 16, 2011 36

Recall: Homomorphic Encryption o H = {Key. Gen, Enc, Dec, Eval} o Semantic security: (pk, Encpk(0)) (pk, Encpk(1)) c* o Homomorphic: Decsk(Evalpk( f, Encpk(x))) = f(x) Ø c* may not look like a “fresh” ciphertext Ø As long as it decrypts to f(x) o Function-private: c* hides f o Compact: Decrypting c* easier than computing f Ø |c*| independent of the complexity of f June 16, 2011 37

Aside: a Trivial Solution o Eval(f, c) = <f, c>, Dec*(<f, c>) = f (Dec(c)) o Neither function-private, nor compact o Not very useful in applications June 16, 2011 38

HE Two-Message SFE o Alice encrypts data x Øsends to Bob c Enc(x) o Bob computes on encrypted data Øsets c* Eval(f, c) Øc* is supposed to be an encryption of f(x) ØHopefully it hides f (function-private scheme) o Alice decrypts, recovers y Dec(c*) June 16, 2011 39

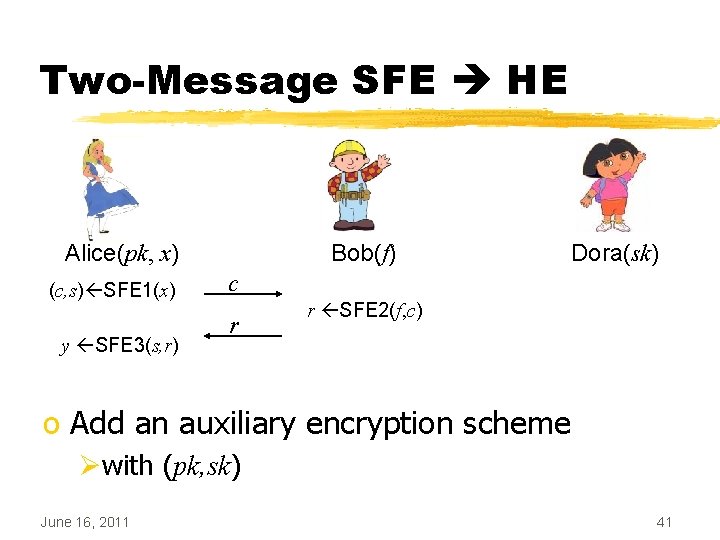
Two-Message SFE HE o Roughly: ØAlice’s message c SFE 1(x) is Enc(x) ØBob’s reply r SFE 2(f, c) is Eval(f, c) o Not quite public-key encryption yet ØWhere are (pk, sk)? ØCan be fixed with an auxiliary PKE scheme June 16, 2011 40

Two-Message SFE HE Alice(pk, Alice(x)x) (c, s) SFE 1(x) y SFE 3(s, r) Bob(f) Dora(sk) c r r SFE 2(f, c) o Add an auxiliary encryption scheme Øwith (pk, sk) June 16, 2011 41

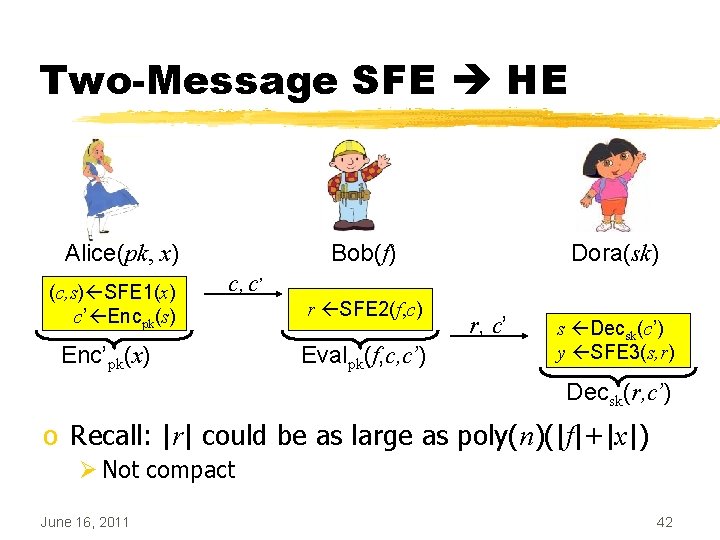
Two-Message SFE HE Alice(pk, x) (c, s) SFE 1(x) c’ Encpk(s) Bob(f) Dora(sk) c, c’ Enc’pk(x) r SFE 2(f, c) Evalpk(f, c, c’) r, c’ s Decsk(c’) y SFE 3(s, r) Decsk(r, c’) o Recall: |r| could be as large as poly(n)(|f|+|x|) Ø Not compact June 16, 2011 42

A More Complex Setting: i-Hop HE [GHV’ 10 b] Alice(x) c 0 Enc(x) Bob(f) c 0 Charlie(g) c 1 Eval(f, c 0) c 1 c 2 Eval(g, c 1) Dora(sk) c 2 y Dec(c 2) 2 -Hop Homomorphic Encryption o c 1 is not a fresh ciphertext Ø May look completely different o Can Charlie process it at all? Ø What about security? June 16, 2011 43

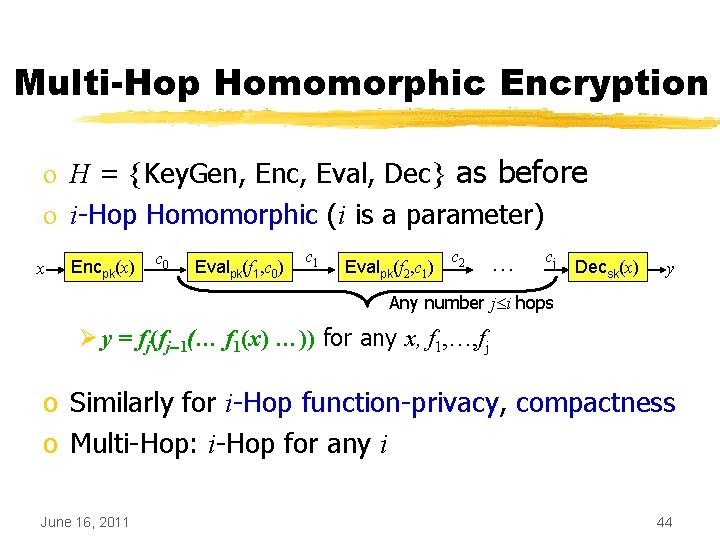
Multi-Hop Homomorphic Encryption o H = {Key. Gen, Enc, Eval, Dec} as before o i-Hop Homomorphic (i is a parameter) x Encpk(x) c 0 Evalpk(f 1, c 0) c 1 Evalpk(f 2, c 1) c 2 … cj Decsk(x) y Any number j i hops Ø y = fj(fj-1(… f 1(x) …)) for any x, f 1, …, fj o Similarly for i-Hop function-privacy, compactness o Multi-Hop: i-Hop for any i June 16, 2011 44

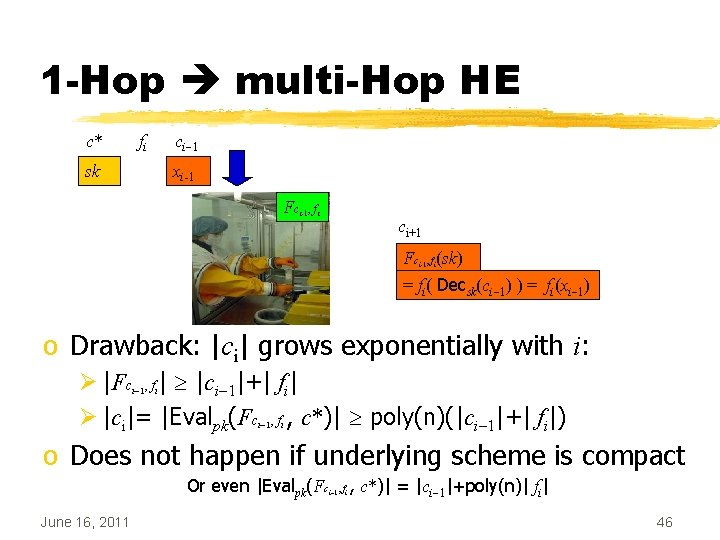
1 -Hop multi-Hop HE o (Key. Gen, Enc, Eval, Dec) is 1 -Hop HE ØCan evaluate any single function on ctxt o We have c 1=Evalpk(f 1, c 0), and some other f 2 Bootstrapping: o Include with pk also c*=Encpk(sk) o Consider Fc , f (sk) = f 2( Decsk(c 1) ) 1 2 ØLet c 2=Evalpk(Fc , f , c*) 1 June 16, 2011 2 45

1 -Hop multi-Hop HE c* fi ci-1 sk xi-1 Fci-1, fi ci+1 Fc , f (sk) = fi( Decsk(ci-1) ) = fi(xi-1) i-1 i o Drawback: |ci| grows exponentially with i: Ø |Fc , f | |ci-1|+| fi| Ø |ci|= |Evalpk(Fc , f , c*)| poly(n)(|ci-1|+| fi|) i-1 i o Does not happen if underlying scheme is compact Or even |Evalpk(Fc June 16, 2011 i-1, fi , c*)| = |ci-1|+poly(n)| fi| 46

Other Constructions o Private 1 -hop HE + Compact 1 -hop HE Compact, Private multi-hop HE o A direct construction of multi-hop HE from Yao’s protocol June 16, 2011 47

Summary o Homomorphic Encryption is useful ØEspecially multi-hop HE o A method for constructing HE schemes from linear ECCs in rings ØTwo (+e) known instances so far o Connection to two-message protocols for secure computation June 16, 2011 48

Thank You