4 Transient Response 4 4 Forced response Natural

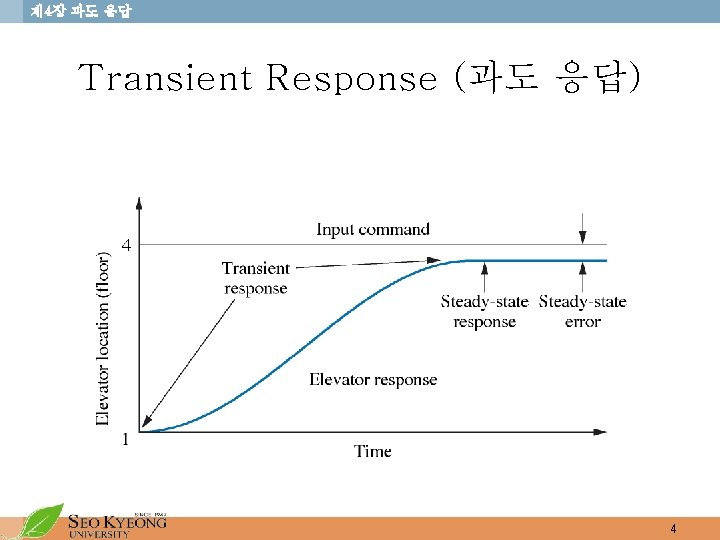
제 4장 과도 응답 Transient Response (과도 응답) 4

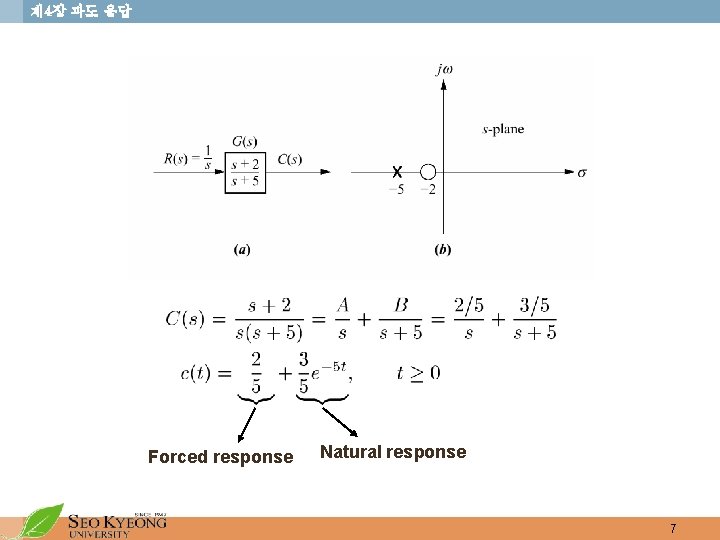
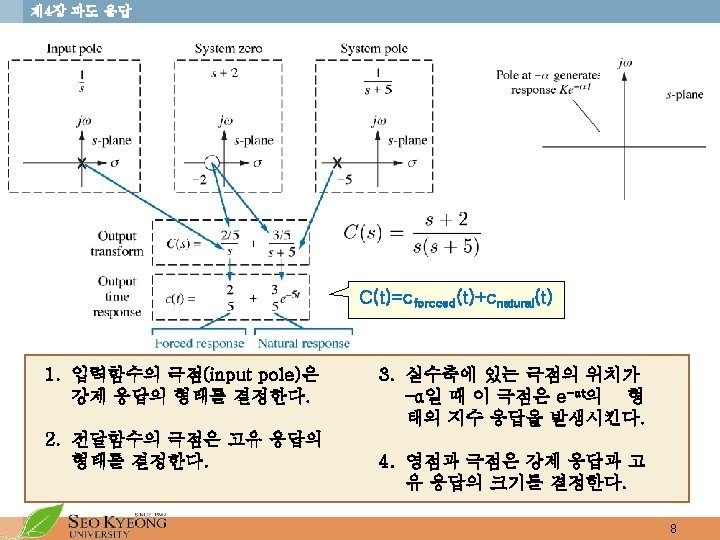
제 4장 과도 응답 Forced response Natural response 7

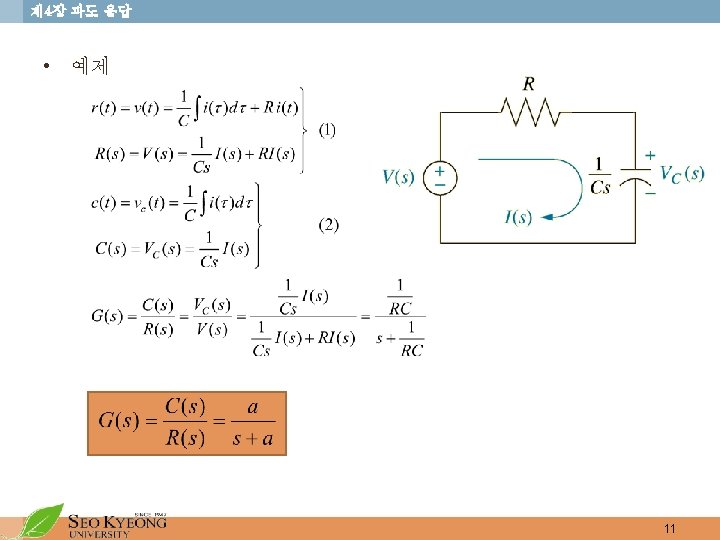
제 4장 과도 응답 • 예제. 4. 1 Forced response Natural response 9

제 4장 과도 응답 1차 시스템 (First-Order System) • If the input is a unit step, • Taking ILT • Where, is forced response (here, is natural response (here, ) ) 10

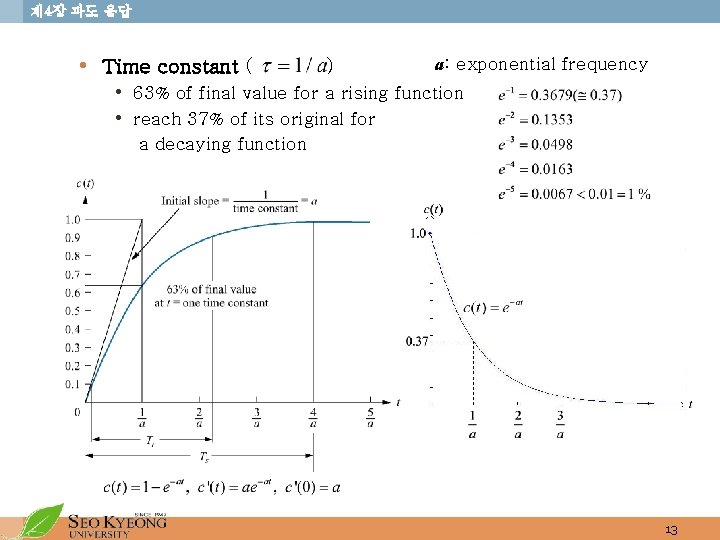
제 4장 과도 응답 • Time constant ( ) a: exponential frequency • 63% of final value for a rising function • reach 37% of its original for a decaying function 13

제 4장 과도 응답 • or • Where, • : time constant : exponential frequency Further the pole from the imaginary axis, the faster the transient response. • Rise Time ( ) • Rise time is defined as the time for the waveform to go from 0. 1 to 0. 9 of its final value. 14

제 4장 과도 응답 • Settling time ( ) • Settling time is defined as the time for the response to reach and stay with 2% of its final value. 15

제 4장 과도 응답 2차 시스템 • The parameters of a second-order system change the form of the response whereas a first-order system change the speed of the response. • Basic system 16

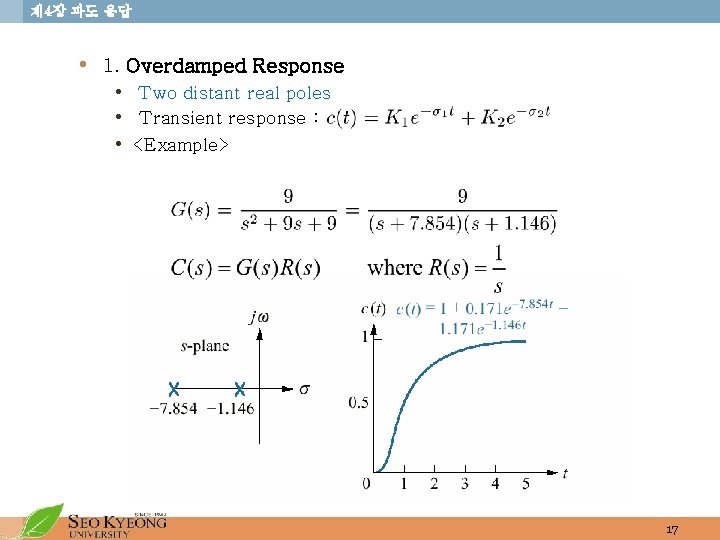
제 4장 과도 응답 • 1. Overdamped Response • Two distant real poles • Transient response : • <Example> 17

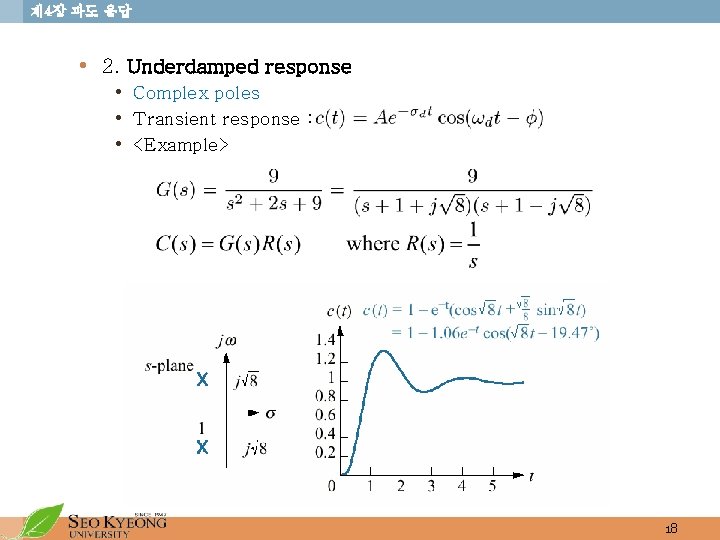
제 4장 과도 응답 • 2. Underdamped response • Complex poles • Transient response : • <Example> 18

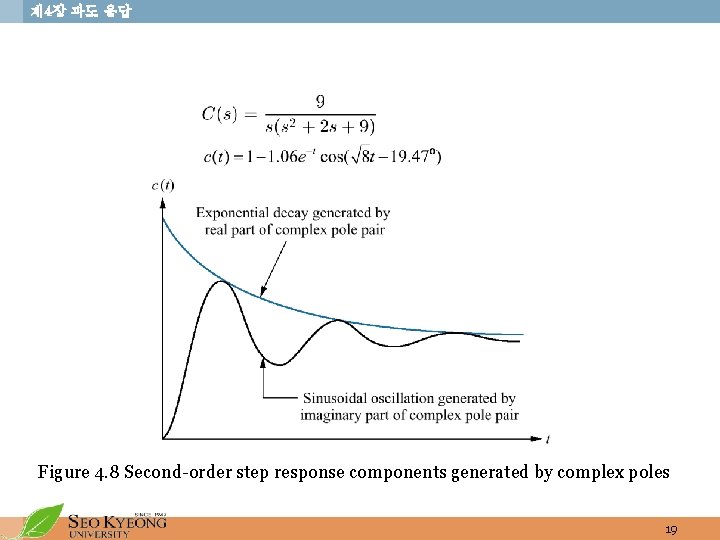
제 4장 과도 응답 Figure 4. 8 Second-order step response components generated by complex poles 19

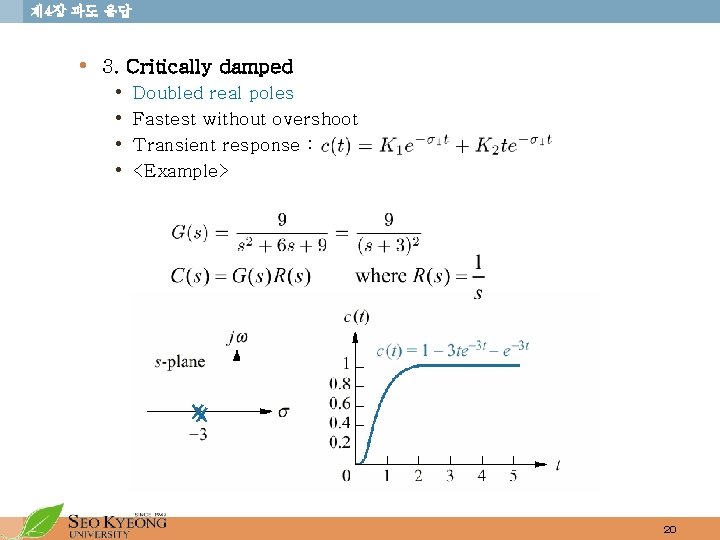
제 4장 과도 응답 • 3. Critically damped • • Doubled real poles Fastest without overshoot Transient response : <Example> 20

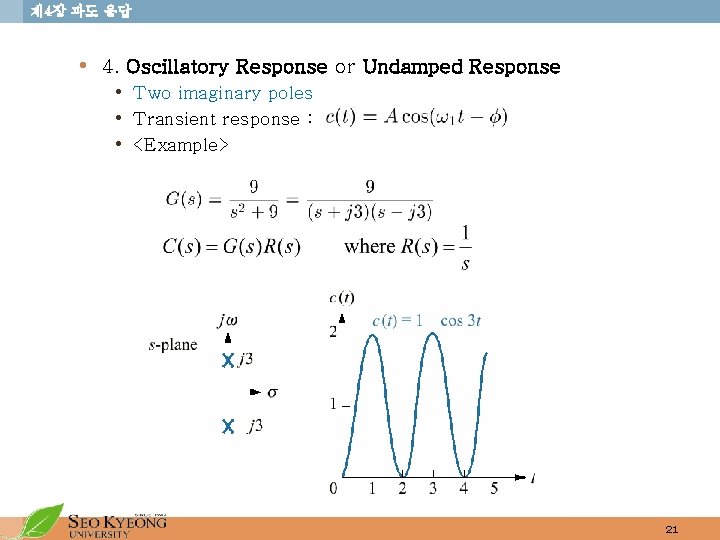
제 4장 과도 응답 • 4. Oscillatory Response or Undamped Response • Two imaginary poles • Transient response : • <Example> 21

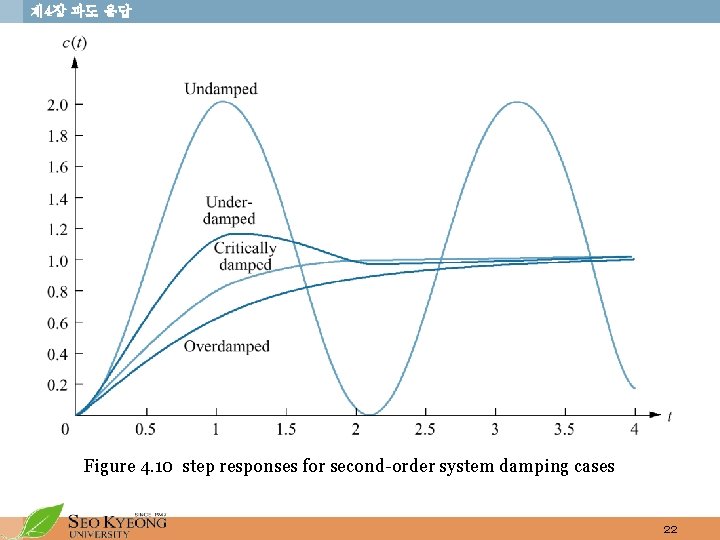
제 4장 과도 응답 Figure 4. 10 step responses for second-order system damping cases 22

제 4장 과도 응답 일반적인 2차 시스템 • Consider the general system • Let a=0, then the G(s) is similar to then • then exponential decay frequency : a/2

제 4장 과도 응답 • distance of the roots from the origin is • From angle, 25

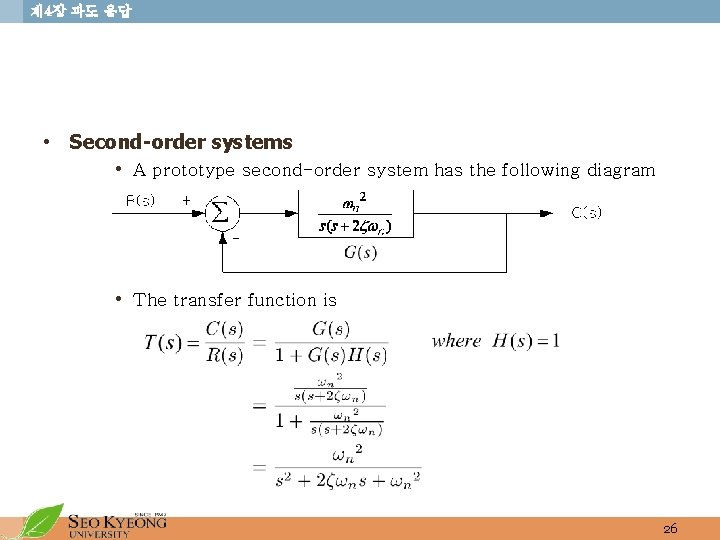
제 4장 과도 응답 • Second-order systems • A prototype second-order system has the following diagram • The transfer function is 26

제 4장 과도 응답 • The response to a unit step input • or is • Taking the ILT yield • Where, 27

제 4장 과도 응답 • There are 4 cases to consider • 1) If , real and unequal roots → The response is said to be overdamped. • 2) If , real and equal roots → The response is said to be critically damped. 29

제 4장 과도 응답 • 3) If complex conjugates roots or → The response is said to be underdamped. • 4) If , imaginary roots → The response is said to be undamped or oscillatory. 30

제 4장 과도 응답 • The system in (2) oscillates at frequency , so is called the natural frequency of the prototype second order system. is the frequency of oscillation of the system without damping. • The system, if underdamped, oscillates at frequency • is called the damped frequency. • The damping of the underdamped system depends on the exponential term • is called the damping factor. • At critical damping, so 31

제 4장 과도 응답 Underdamped Second-Order Systems 32

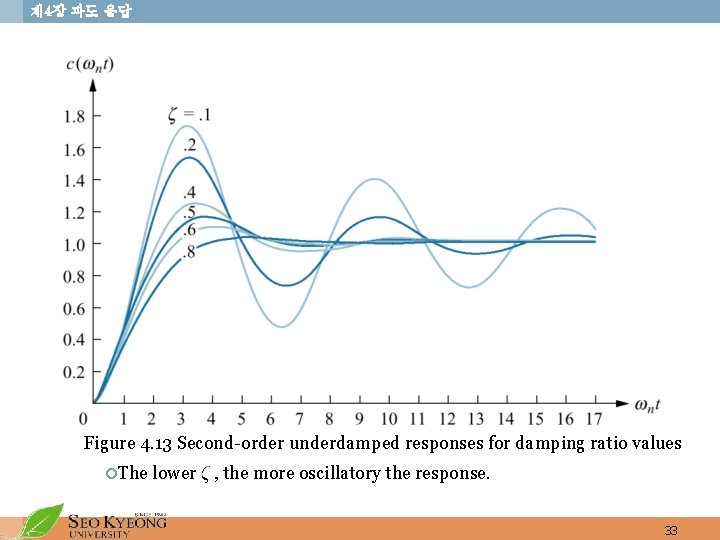
제 4장 과도 응답 Figure 4. 13 Second-order underdamped responses for damping ratio values ¡The lower , the more oscillatory the response. 33

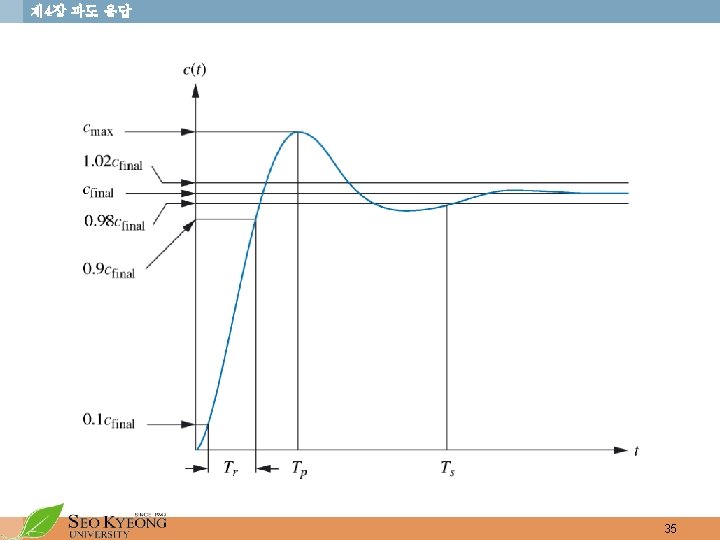
제 4장 과도 응답 • Evaluation of the peak time or Maximum overshoots • The response of the prototype second-order system to a unitstep input is • The derivative : when set to zero, gives the necessary condition for the relative minima and maxima. We get 36

제 4장 과도 응답 • For (1) to be satisfied, we have the possible solutions It gives • The maxima can be found be taking the second derivative or by evaluating for various From (1) it should be easy to see that the first relative maximum occurs at 37

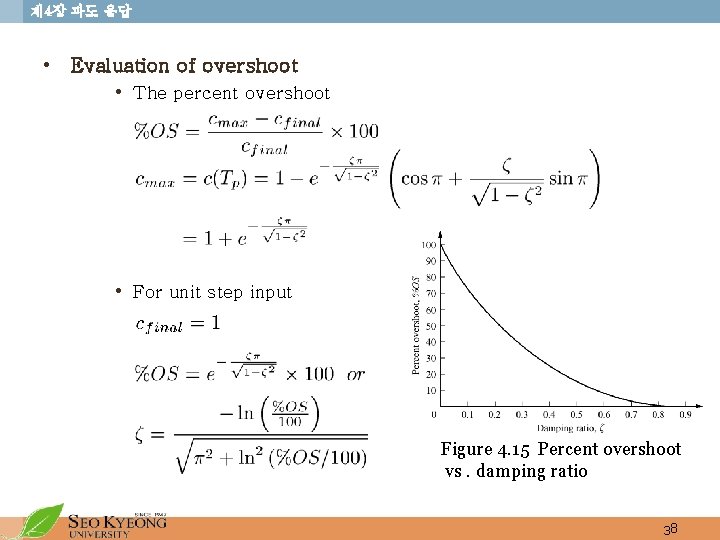
제 4장 과도 응답 • Evaluation of overshoot • The percent overshoot • For unit step input Figure 4. 15 Percent overshoot vs. damping ratio 38

제 4장 과도 응답 • Evaluation of (overshoot 2%) 39

제 4장 과도 응답 • The relationship between ( , %OS , underdamped second-order system. ) and ( ) for • Here, poles are Figure 4. 17 Pole plot for an underdamped second-order system 40

제 4장 과도 응답 • Let • Then, • Real part: Exponential damping frequency • Imaginary part: Damped frequency of oscillation • • : inversely proportional to • : only a function of 41

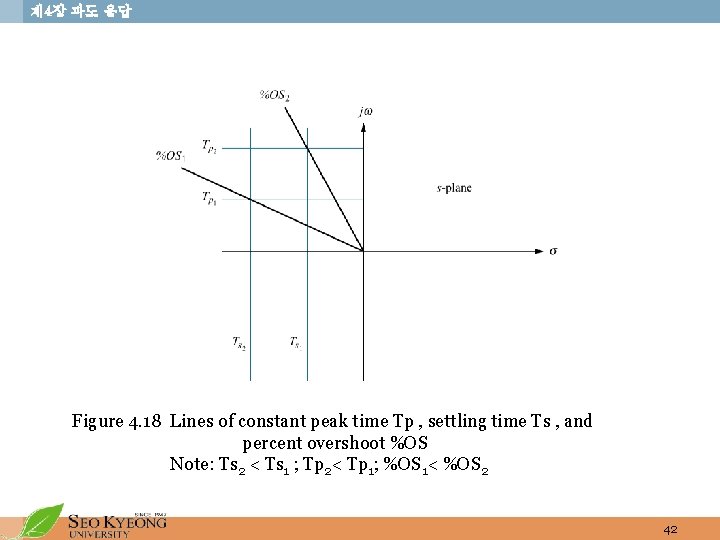
제 4장 과도 응답 Figure 4. 18 Lines of constant peak time Tp , settling time Ts , and percent overshoot %OS Note: Ts 2 < Ts 1 ; Tp 2< Tp 1; %OS 1< %OS 2 42

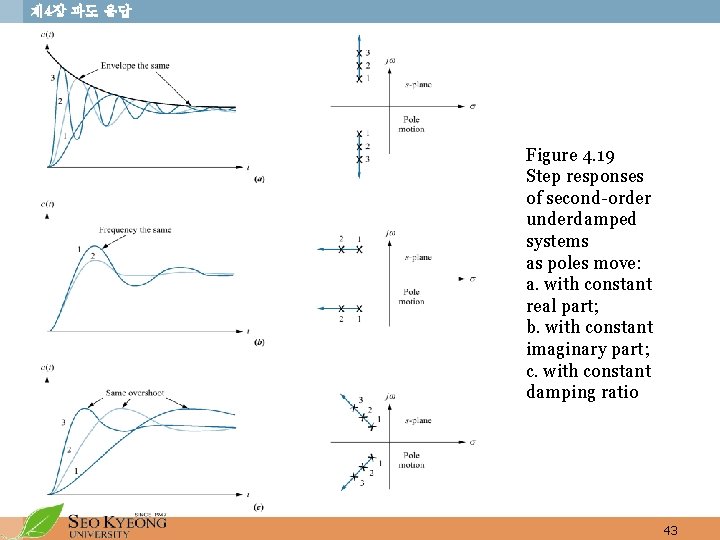
제 4장 과도 응답 Figure 4. 19 Step responses of second-order underdamped systems as poles move: a. with constant real part; b. with constant imaginary part; c. with constant damping ratio 43

제 4장 과도 응답 • EX) Given the following circuit, find 44

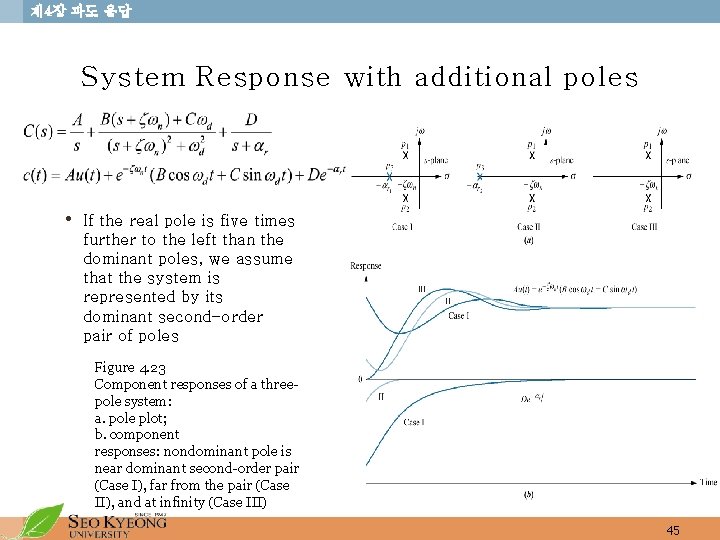
제 4장 과도 응답 System Response with additional poles • If the real pole is five times further to the left than the dominant poles, we assume that the system is represented by its dominant second-order pair of poles Figure 4. 23 Component responses of a threepole system: a. pole plot; b. component responses: nondominant pole is near dominant second-order pair (Case I), far from the pair (Case II), and at infinity (Case III) 45

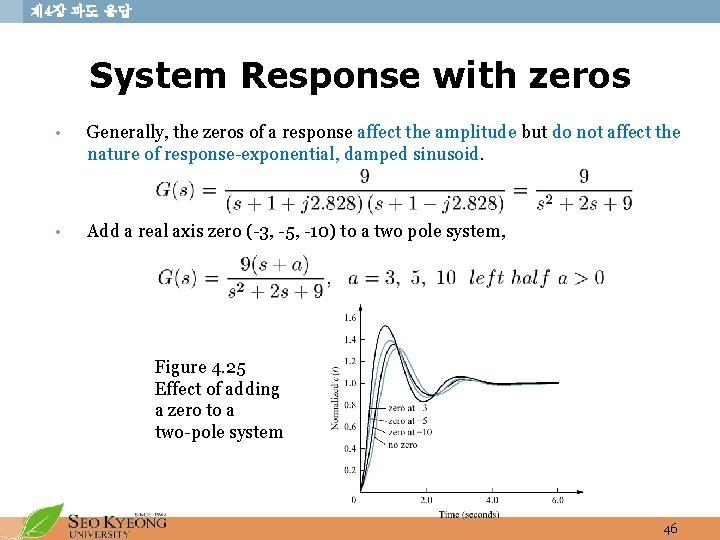
제 4장 과도 응답 System Response with zeros • Generally, the zeros of a response affect the amplitude but do not affect the nature of response-exponential, damped sinusoid. • Add a real axis zero (-3, -5, -10) to a two pole system, Figure 4. 25 Effect of adding a zero to a two-pole system 46

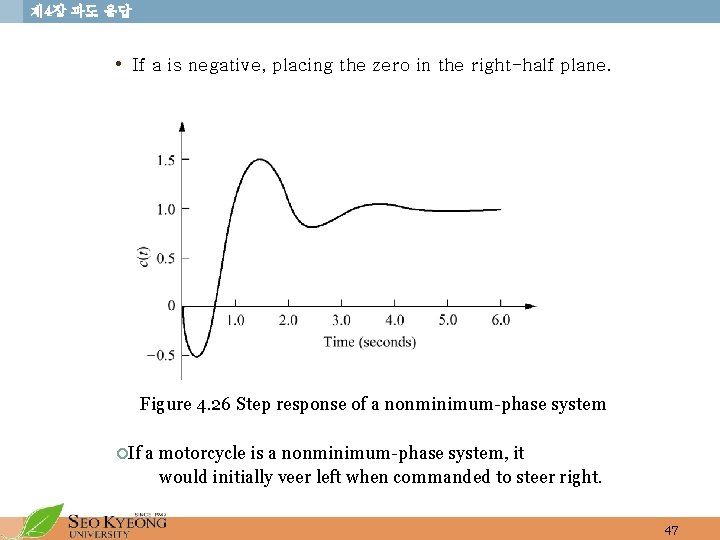
제 4장 과도 응답 • If a is negative, placing the zero in the right-half plane. Figure 4. 26 Step response of a nonminimum-phase system ¡If a motorcycle is a nonminimum-phase system, it would initially veer left when commanded to steer right. 47

제 4장 과도 응답 • Effect of zeros • Analysis I • If the zero is far from the poles, then a is large compared to b and c • The zero look like a simple gain factor and does not change the relative amplitudes of the components of the response. 48

제 4장 과도 응답 • Analysis 2 • Another way to look at the effect of zero • add a zero to a transfer function derivative version • If , and scaled version is very large, is a scaled version of original response. • If , and is not very large, both response important. • If , and is very small, derivative term dominate more overshoot in the second-order system. • If , nonminimum-phase, opposite directions (a. C(s), s. C(s)) 49

제 4장 과도 응답 • Pole-Zero cancellation • PFE, 50