Dynamic Response Unit step signal Step response ysHss












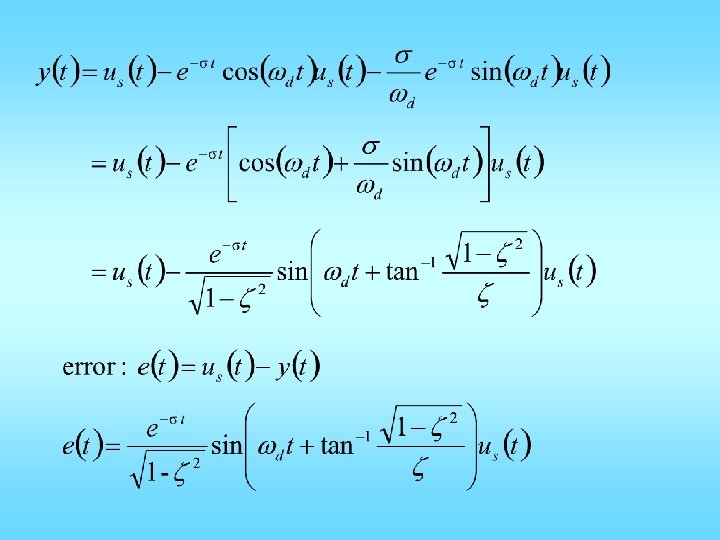
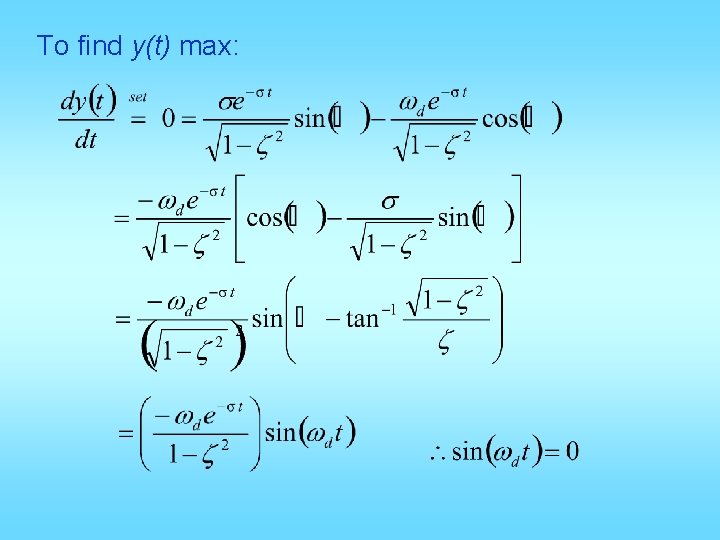


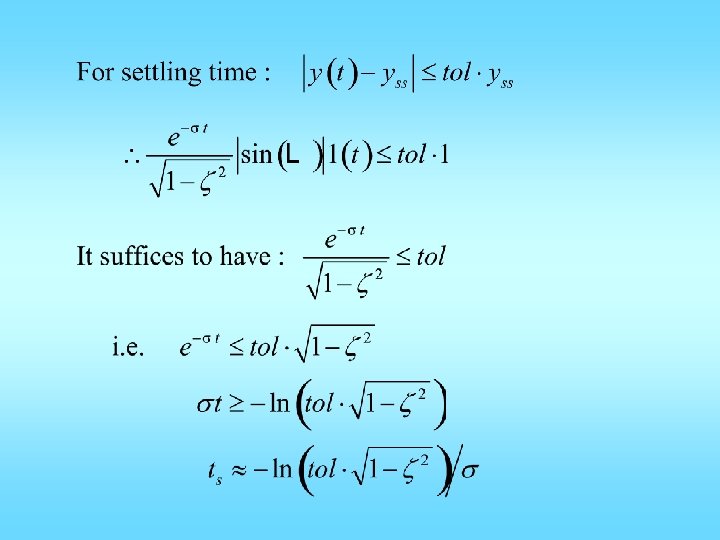



- Slides: 34

Dynamic Response • Unit step signal: • Step response: y(s)=H(s)/s, y(t)=L-1{H(s)/s} Time domain response specifications • Defined based on unit step response • Defined for closed-loop system


Transient Response • First order system transient response – Step response specs and relationship to pole location • Second order system transient response – Step response specs and relationship to pole location • Effects of additional poles and zeros

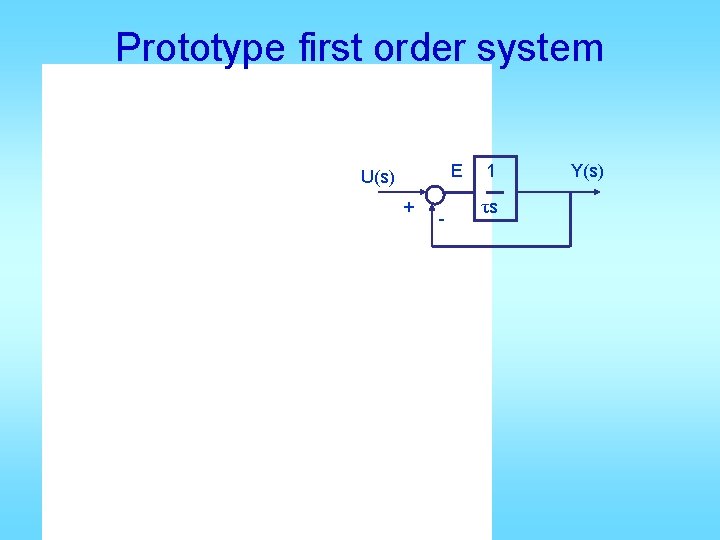
Prototype first order system E U(s) + - 1 τs Y(s)

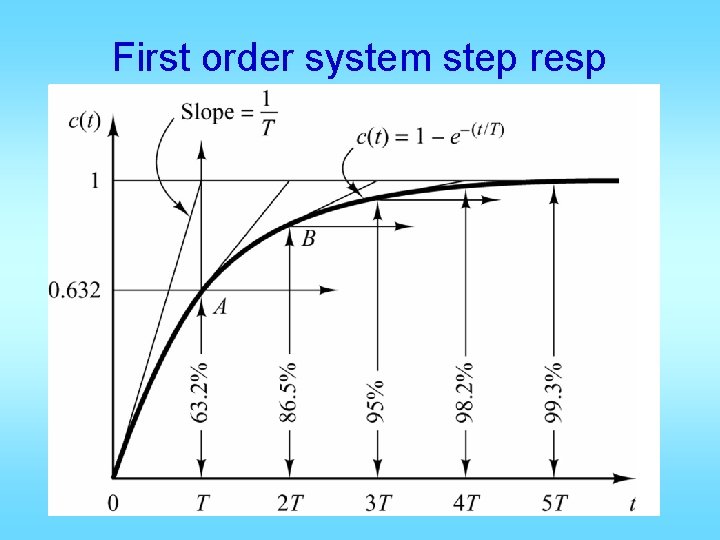
First order system step resp Normalized time t/t

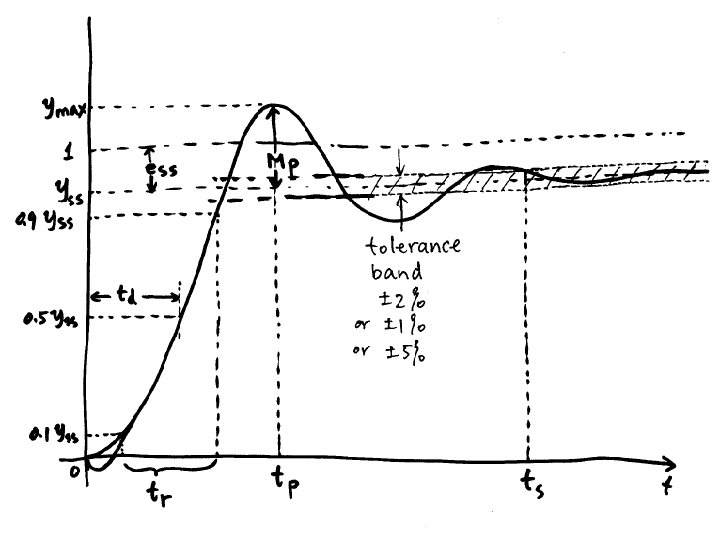
Prototype first order system • • • No overshoot, tp=inf, Mp = 0 Yss=1, ess=0 Settling time ts = [-ln(tol)]/p Delay time td = [-ln(0. 5)]/p Rise time tr = [ln(0. 9) – ln(0. 1)]/p • All times proportional to 1/p= t • Larger p means faster response

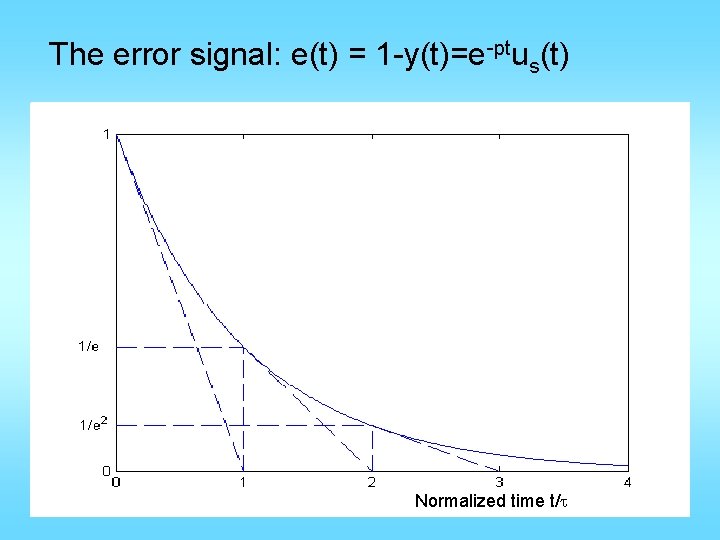
The error signal: e(t) = 1 -y(t)=e-ptus(t) Normalized time t/t

In every τ seconds, the error is reduced by 63. 2%

General First-order system We know how this responds to input Step response starts at y(0+)=k, final value kz/p 1/p = t is still time constant; in every t, y(t) moves 63. 2% closer to final value

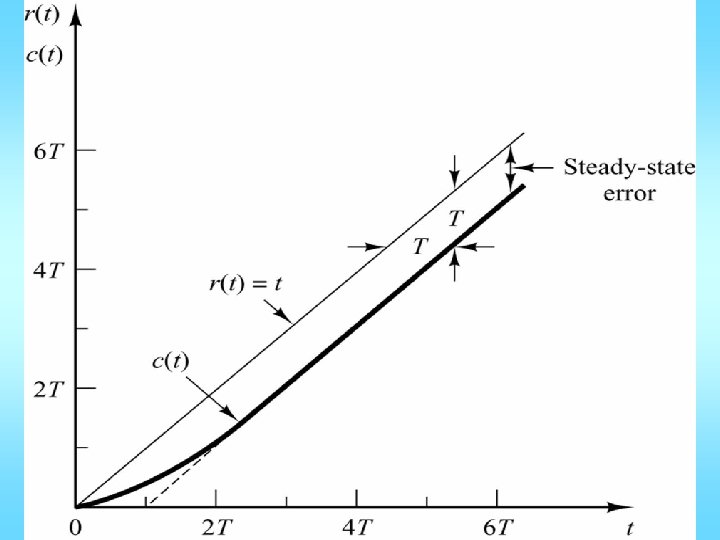
Unit ramp response:


Note: In step response, the steady-state tracking error = zero.

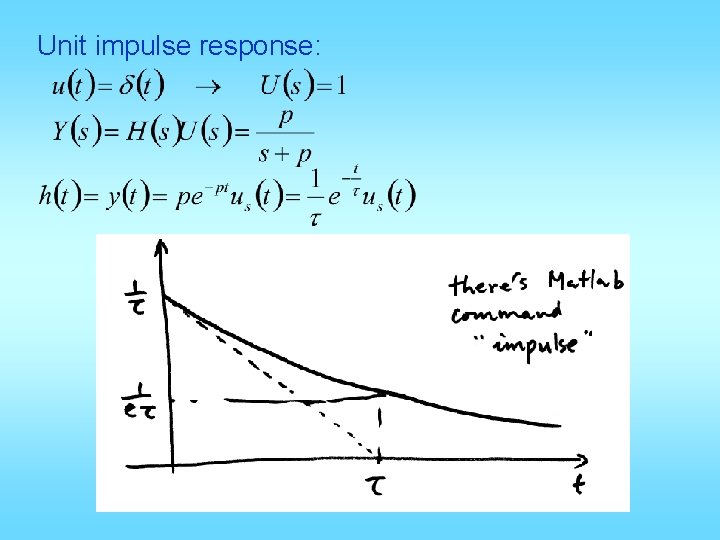
Unit impulse response:

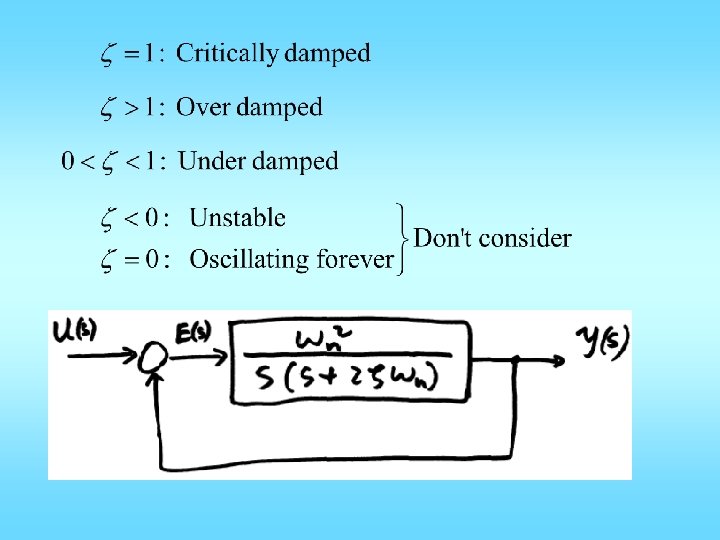
Prototype nd 2 order system:



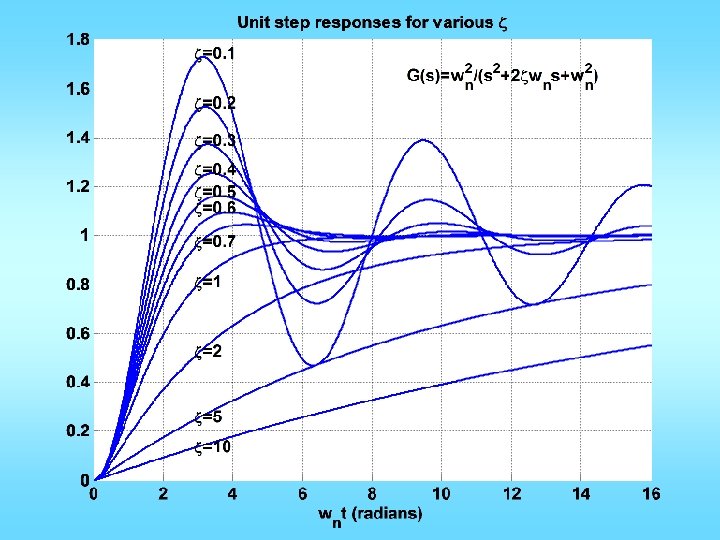
xi=[0. 7 1 2 5 10 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6]; x=['zeta=0. 7'; 'zeta=1 '; 'zeta=2 '; 'zeta=5 '; 'zeta=10 '; 'zeta=0. 1'; 'zeta=0. 2'; 'zeta=0. 3'; 'zeta=0. 4'; 'zeta=0. 5'; 'zeta=0. 6']; T=0: 0. 01: 16; figure; hold; for k=1: length(xi) n=[1]; d=[1 2*xi(k) 1]; y=step(n, d, T); plot(T, y); if xi(k)>=0. 7 text(T(290), y(310), x(k, : )); else text(T(290), max(y)+0. 02, x(k, : )); end grid; end text(9, 1. 65, 'G(s)=w_n^2/(s^2+2zetaw_ns+w_n^2)') title('Unit step responses for various zeta') xlabel('w_nt (radians)') Can use omega in stead of w

annotation Create annotations including lines, arrows, text arrows, double arrows, text boxes, rectangles, and ellipses xlabel, ylabel, zlabel Add a text label to the respective axis title Add a title to a graph colorbar Add a colorbar to a graph legend Add a legend to a graph

For example: “help annotation” explains how to use the annotation command to add text, lines, arrows, and so on at desired positions in the graph ANNOTATION('textbox', POSITION) creates a textbox annotation at the position specified in normalized figure units by the vector POSITION ANNOTATION('line', X, Y) creates a line annotation with endpoints specified in normalized figure coordinates by the vectors X and Y ANNOTATION('arrow', X, Y) creates an arrow annotation with endpoints specified Example: ah=annotation('arrow', [. 9. 5], [. 9, . 5], 'Color', 'r'); th=annotation('textarrow', [. 3, . 6], [. 7, . 4], 'String', 'ABC');

Unit step response: 1) Under damped, 0 < ζ < 1

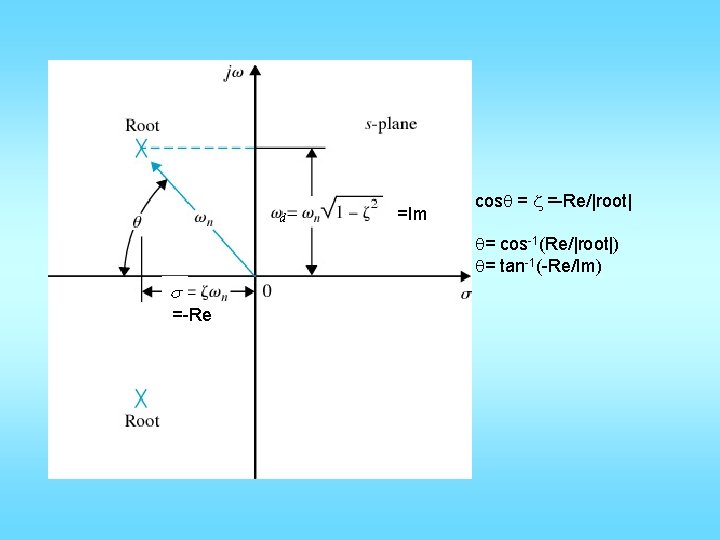
d =Im cosq = z =-Re/|root| q= cos-1(Re/|root|) q= tan-1(-Re/Im) s =-Re
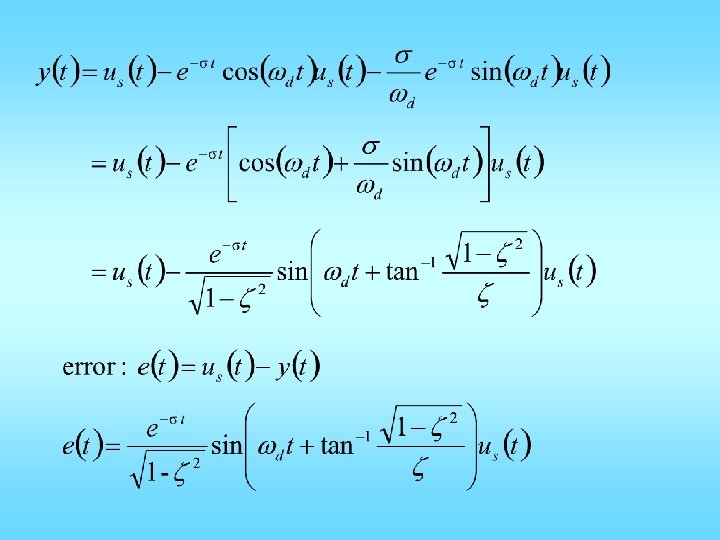
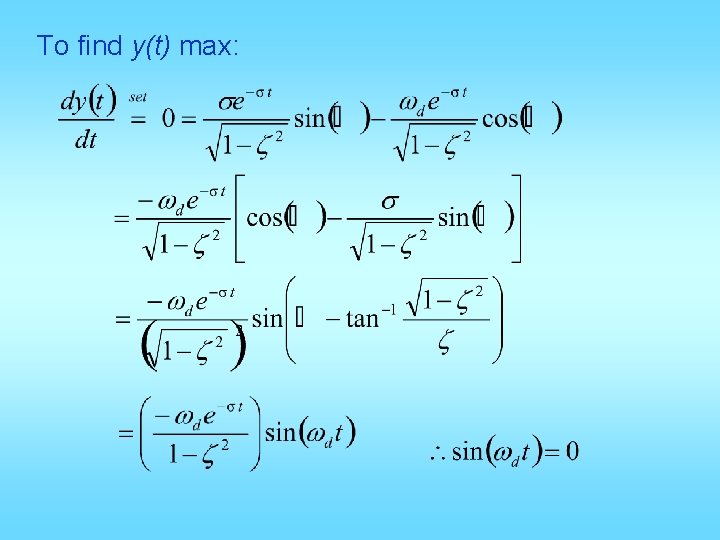
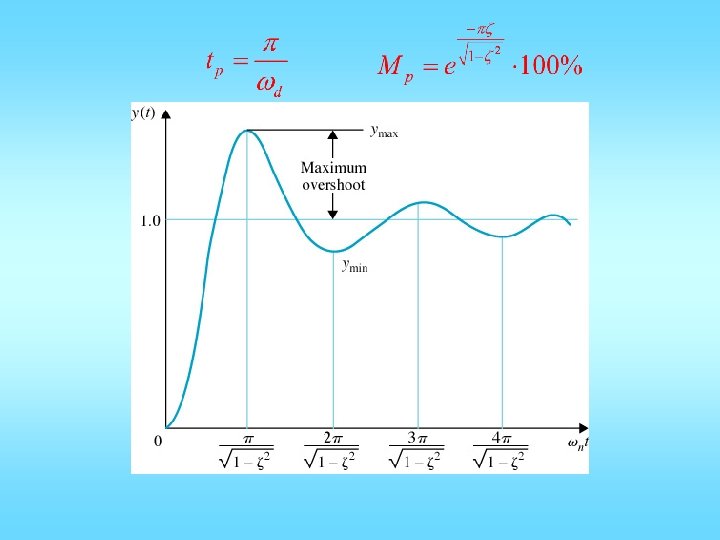
To find y(t) max:



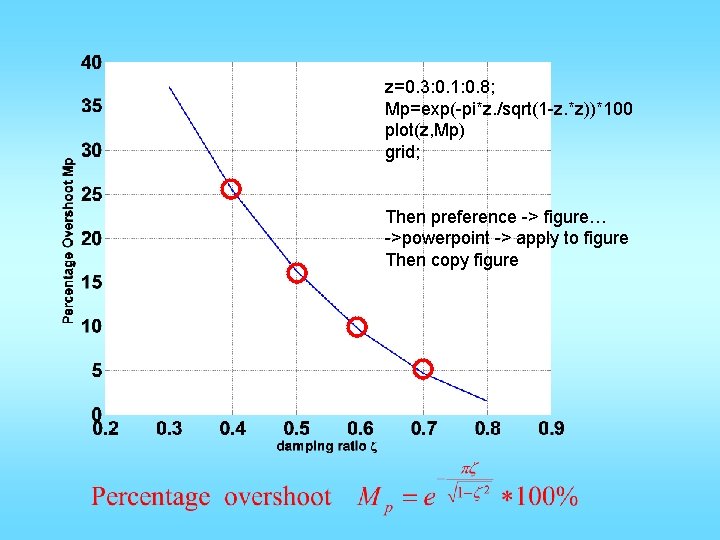
z=0. 3: 0. 1: 0. 8; Mp=exp(-pi*z. /sqrt(1 -z. *z))*100 plot(z, Mp) grid; Then preference -> figure… ->powerpoint -> apply to figure Then copy figure

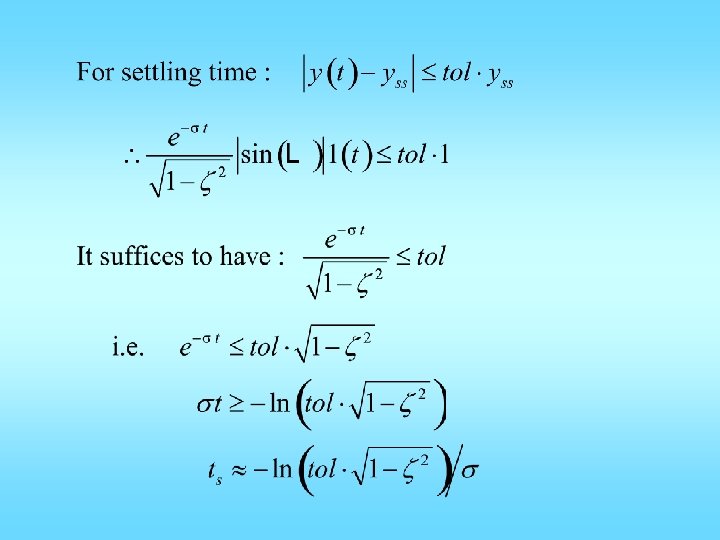


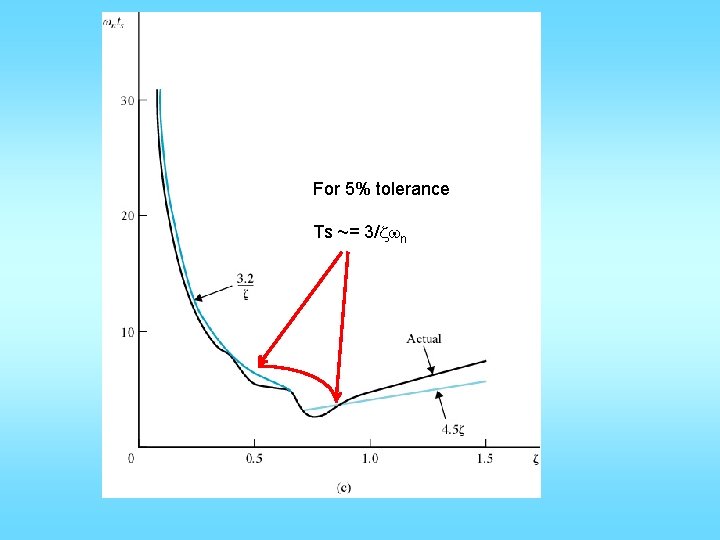
For 5% tolerance Ts ~= 3/zwn

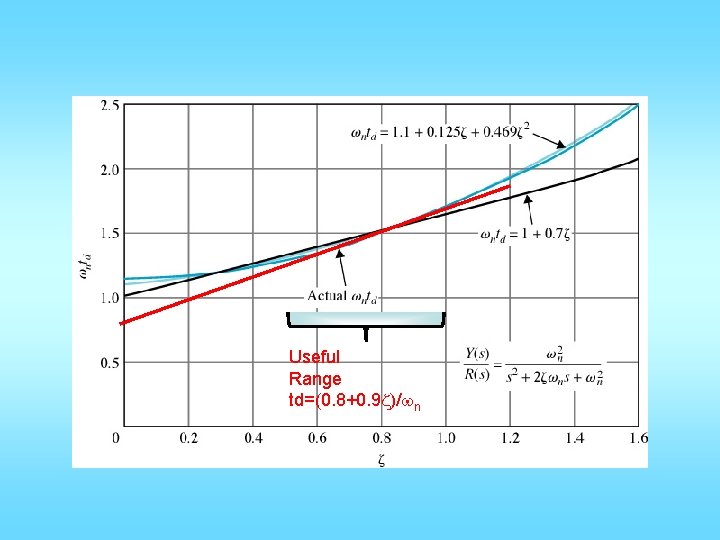
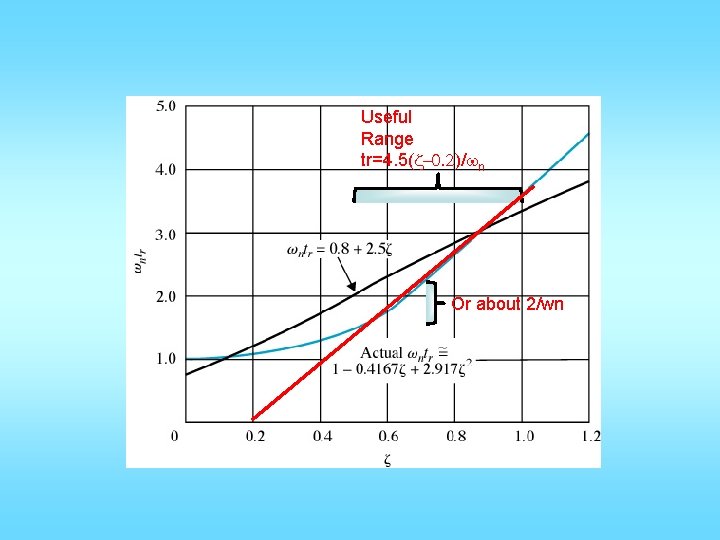
• Delay time is not used very much • For delay time, solve y(t)=0. 5 and solve for t • For rise time, set y(t) = 0. 1 & 0. 9, solve for t • This is very difficult • Based on numerical simulation:

Useful Range td=(0. 8+0. 9 z)/wn

Useful Range tr=4. 5(z-0. 2)/wn Or about 2/wn

Putting all things together: Settling time:
 Step 1 step 2 step 3 step 4
Step 1 step 2 step 3 step 4 Step response
Step response What is laplace transform
What is laplace transform Baseband signal and bandpass signal
Baseband signal and bandpass signal Baseband signal and bandpass signal
Baseband signal and bandpass signal Digital signal as a composite analog signal
Digital signal as a composite analog signal Classification of signals
Classification of signals Dynamic dynamic - bloom
Dynamic dynamic - bloom Stimulus-response model
Stimulus-response model Stimulus receptor signal response
Stimulus receptor signal response Stimulus receptor signal response
Stimulus receptor signal response Unit 6 review questions
Unit 6 review questions What is dynamic response in control system
What is dynamic response in control system Unit doublet signal
Unit doublet signal Natural response and forced response
Natural response and forced response Natural response circuit
Natural response circuit Primary immune response and secondary immune response
Primary immune response and secondary immune response First order rc
First order rc Rl circuit natural response
Rl circuit natural response Disking teeth
Disking teeth Creating a dinosaur sculpture type of graphic organizer
Creating a dinosaur sculpture type of graphic organizer Informative essay outline
Informative essay outline Body paragraph starters
Body paragraph starters Step back step up
Step back step up How to factor equations
How to factor equations Simultaneous equations step by step
Simultaneous equations step by step Simultaneous equations step by step
Simultaneous equations step by step Combining like terms steps
Combining like terms steps The process of photosynthesis step by step
The process of photosynthesis step by step Bayes filter matlab
Bayes filter matlab Real application testing
Real application testing Netbackup bare metal restore step by step
Netbackup bare metal restore step by step Solving trigonometric equations
Solving trigonometric equations Linda evangelista face shape
Linda evangelista face shape Step by step punnett square
Step by step punnett square