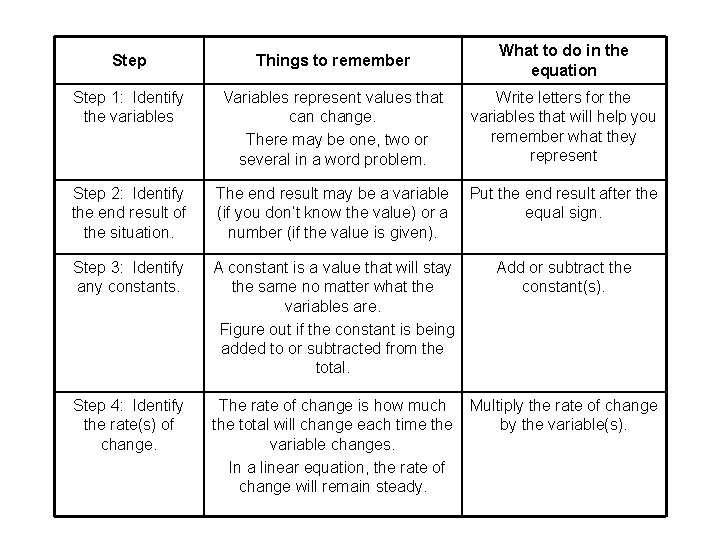
Step 1 Step 2 Step 3 Step 4










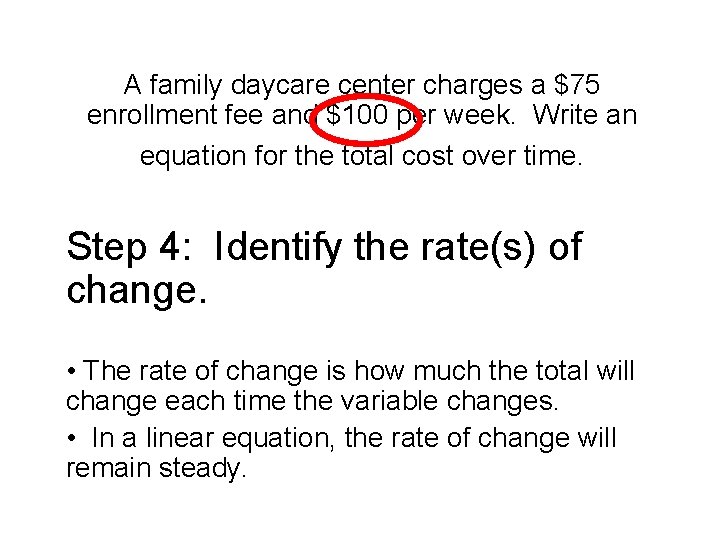

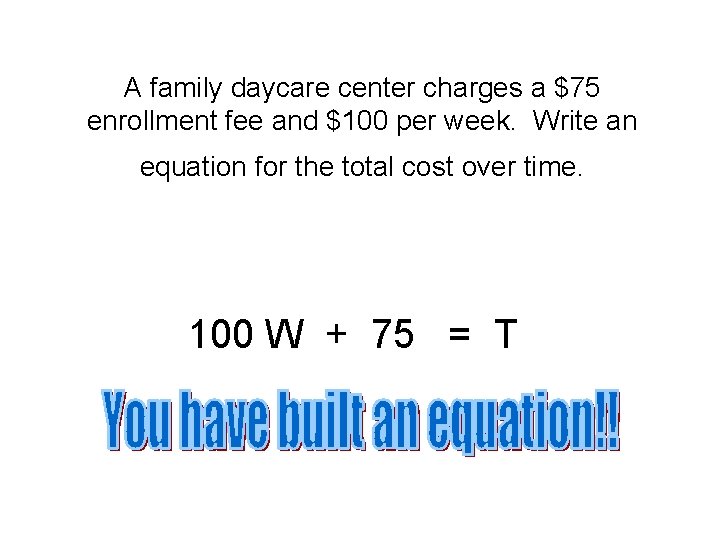



















- Slides: 35


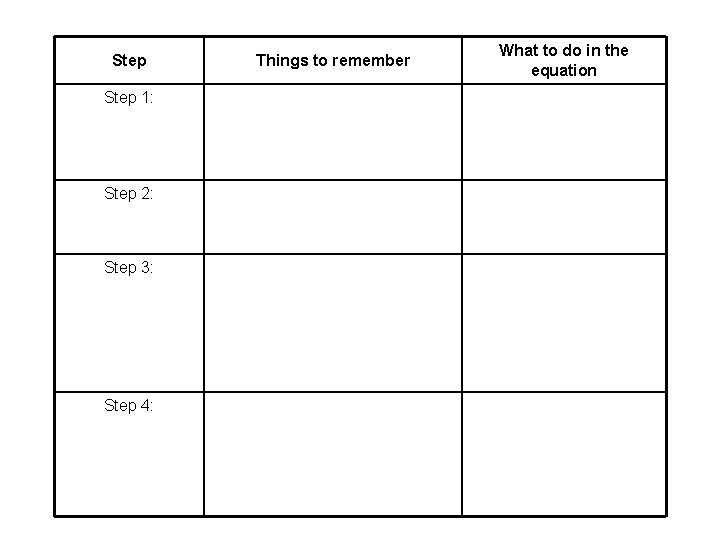
Step 1: Step 2: Step 3: Step 4: Things to remember What to do in the equation

HINT WORDS • Addition: add, plus, increased, sum, more than, in addition • Subtraction: difference, less than, decreased, minus, declines • Multiply: multiply, per, each, installments, percent, of, times • Divide: divided by, split, quotient, per

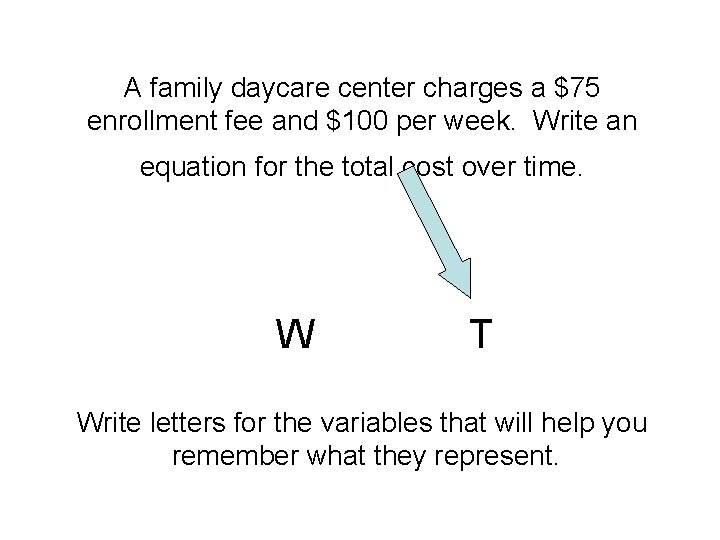
A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time.

A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. Step 1: Identify the variables • Variables represent values that can change. • There may be one, two or several in a word problem.

A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. W Write letters for the variables that will help you remember what they represent.

A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. W T Write letters for the variables that will help you remember what they represent.

A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. Step 2: Identify the end result of the situation. • This may be a variable (if you don’t know the value) or a number (if the value is given).

A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. W T Put the end result after the equal sign.

A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. W = T Put the end result after the equal sign.

A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. Step 3: Identify any constants. • A constant is a value that will stay the same no matter what the variables are. • Figure out if the constant is being added to or subtracted from the total.

A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. W + 75 = T Add or subtract the constant(s).
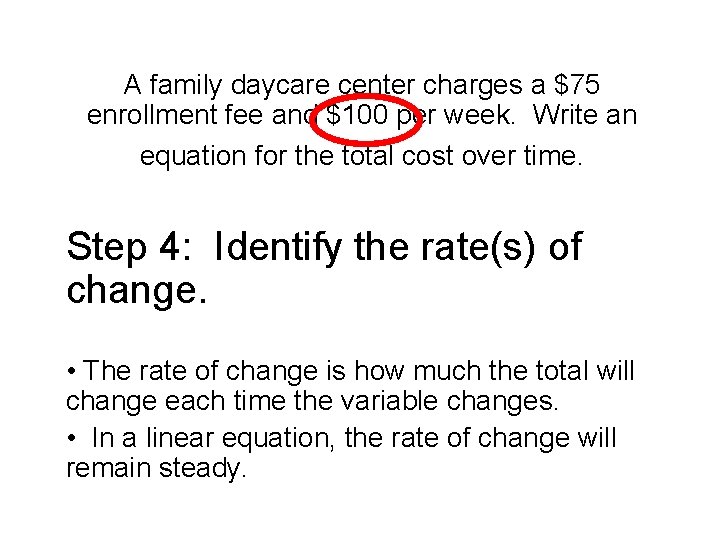
A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. Step 4: Identify the rate(s) of change. • The rate of change is how much the total will change each time the variable changes. • In a linear equation, the rate of change will remain steady.

A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. 100 W + 75 = T Multiply the rate of change by the variable(s).
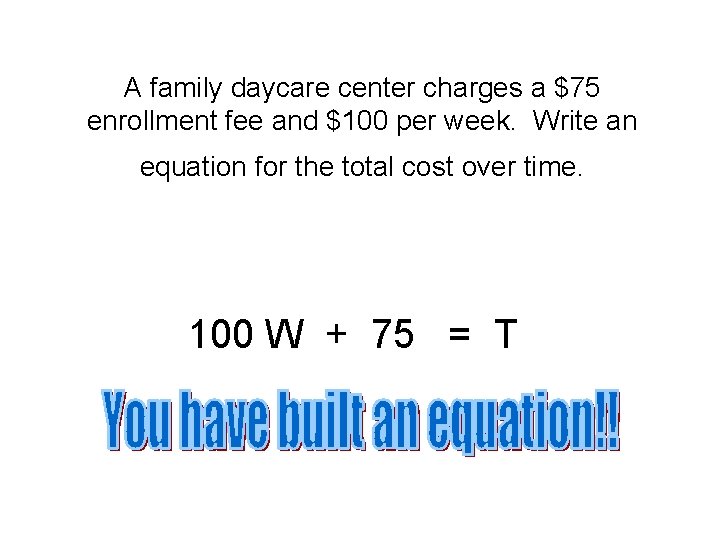
A family daycare center charges a $75 enrollment fee and $100 per week. Write an equation for the total cost over time. 100 W + 75 = T

Next problem: The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time.

The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time. Step 1: Identify the variables

The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time. W T Step 1: Identify the variables

The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time. W T Step 1: Identify the variables. Step 2: Identify the end result of the situation

The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time. W = T Step 1: Identify the variables. Step 2: Identify the end result of the situation

The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time. W = T Step 1: Identify the variables. Step 2: Identify the end result of the situation Step 3: Identify any constants.

The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time. None! W = T Step 1: Identify the variables. Step 2: Identify the end result of the situation Step 3: Identify any constants.

The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time. W = T Step 1: Identify the variables. Step 2: Identify the end result of the situation Step 3: Identify any constants. Step 4: Identify the rate(s) of change.

The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time. 110 W = T Step 1: Identify the variables. Step 2: Identify the end result of the situation Step 3: Identify any constants. Step 4: Identify the rate(s) of change.

The daycare center down the street charges no enrollment fee, but $110 per week. Write an equation for the total cost over time. 110 W = T

Naima and her friends have $40 to spend at the movie theater. Each large popcorn costs $5 and each small soda costs $2. Write an equation for the number of snacks she can buy with the money she has.

Naima and her friends have $40 to spend at the movie theater. Each large popcorn costs $5 and each small soda costs $2. Write an equation for the number of snacks she can buy with the money she has. Step 1: Identify the variables

Naima and her friends have $40 to spend at the movie theater. Each large popcorn costs $5 and each small soda costs $2. Write an equation for the number of snacks she can buy with the money she has. P S Step 1: Identify the variables

Naima and her friends have $40 to spend at the movie theater. Each large popcorn costs $5 and each small soda costs $2. Write an equation for the number of snacks she can buy with the money she has. P S Step 1: Identify the variables. Step 2: Identify the end result of the situation

Naima and her friends have $40 to spend at the movie theater. Each large popcorn costs $5 and each small soda costs $2. Write an equation for the number of snacks she can buy with the money she has. P S = 40 Step 1: Identify the variables. Step 2: Identify the end result of the situation

Naima and her friends have $40 to spend at the movie theater. Each large popcorn costs $5 and each small soda costs $2. Write an equation for the number of snacks she can buy with the money she has. None! P S = 40 Step 1: Identify the variables. Step 2: Identify the end result of the situation Step 3: Identify any constants.

Naima and her friends have $40 to spend at the movie theater. Each large popcorn costs $5 and each small soda costs $2. Write an equation for the number of snacks she can buy with the money she has. P S = 40 Step 1: Identify the variables. Step 2: Identify the end result of the situation Step 3: Identify any constants. Step 4: Identify the rate(s) of change.

Naima and her friends have $40 to spend at the movie theater. Each large popcorn costs $5 and each small soda costs $2. Write an equation for the number of snacks she can buy with the money she has. 5 P 2 S = 40 Step 1: Identify the variables. Step 2: Identify the end result of the situation Step 3: Identify any constants. Step 4: Identify the rate(s) of change.

Naima and her friends have $40 to spend at the movie theater. Each large popcorn costs $5 and each small soda costs $2. Write an equation for the number of snacks she can buy with the money she has. 5 P + 2 S = 40

Step Things to remember What to do in the equation Step 1: Identify the variables Variables represent values that can change. There may be one, two or several in a word problem. Write letters for the variables that will help you remember what they represent Step 2: Identify the end result of the situation. The end result may be a variable (if you don’t know the value) or a number (if the value is given). Put the end result after the equal sign. Step 3: Identify any constants. A constant is a value that will stay the same no matter what the variables are. Figure out if the constant is being added to or subtracted from the total. Add or subtract the constant(s). Step 4: Identify the rate(s) of change. The rate of change is how much the total will change each time the variable changes. In a linear equation, the rate of change will remain steady. Multiply the rate of change by the variable(s).