Response of FirstOrder Circuits RL Circuits RC Circuits






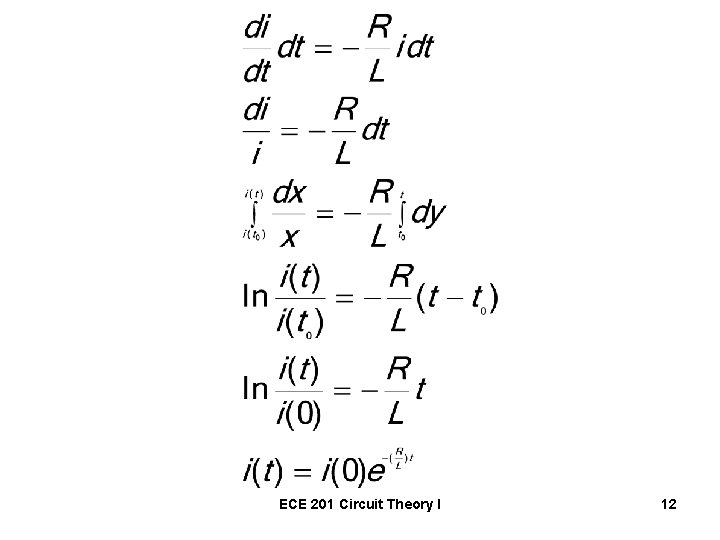





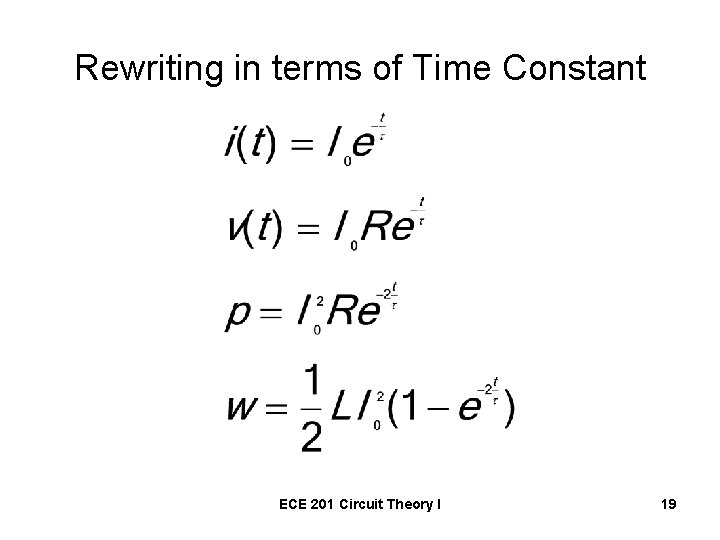



- Slides: 23

Response of First-Order Circuits RL Circuits RC Circuits ECE 201 Circuit Theory I 1

The Natural Response of a Circuit • The currents and voltages that arise when energy stored in an inductor or capacitor is suddenly released into a resistive circuit. • These “signals” are determined by the circuit itself, not by external sources! ECE 201 Circuit Theory I 2

Step Response • The sudden application of a DC voltage or current source is referred to as a “step”. • The step response consists of the voltages and currents that arise when energy is being absorbed by an inductor or capacitor. ECE 201 Circuit Theory I 3

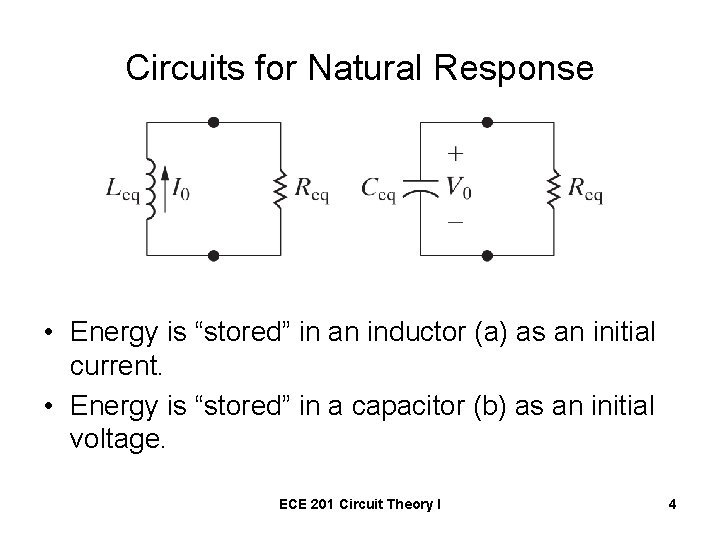
Circuits for Natural Response • Energy is “stored” in an inductor (a) as an initial current. • Energy is “stored” in a capacitor (b) as an initial voltage. ECE 201 Circuit Theory I 4

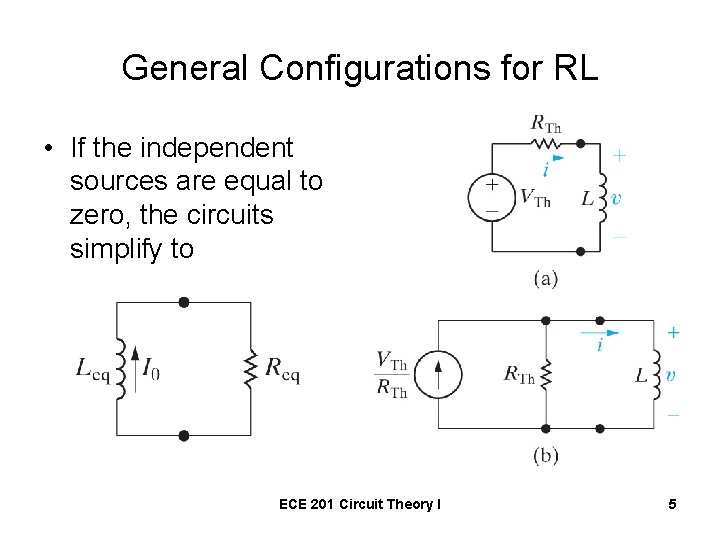
General Configurations for RL • If the independent sources are equal to zero, the circuits simplify to ECE 201 Circuit Theory I 5

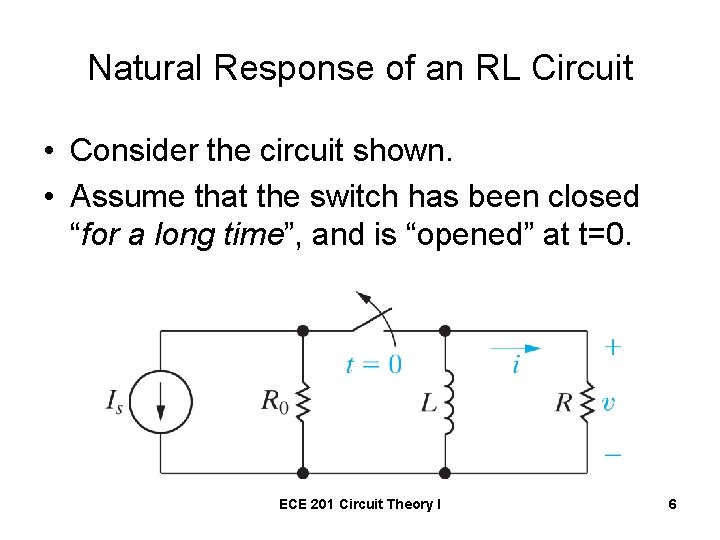
Natural Response of an RL Circuit • Consider the circuit shown. • Assume that the switch has been closed “for a long time”, and is “opened” at t=0. ECE 201 Circuit Theory I 6

What does “for a long time” Mean? • All of the currents and voltages have reached a constant (dc) value. • What is the voltage across the inductor just before the switch is opened? ECE 201 Circuit Theory I 7

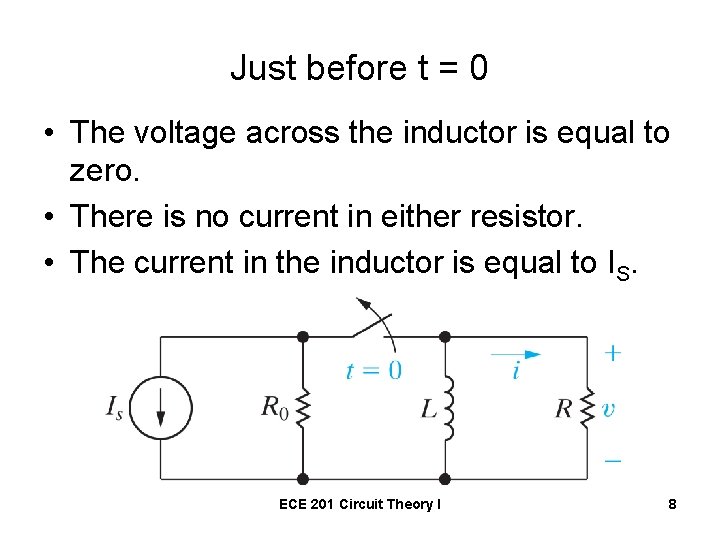
Just before t = 0 • The voltage across the inductor is equal to zero. • There is no current in either resistor. • The current in the inductor is equal to IS. ECE 201 Circuit Theory I 8

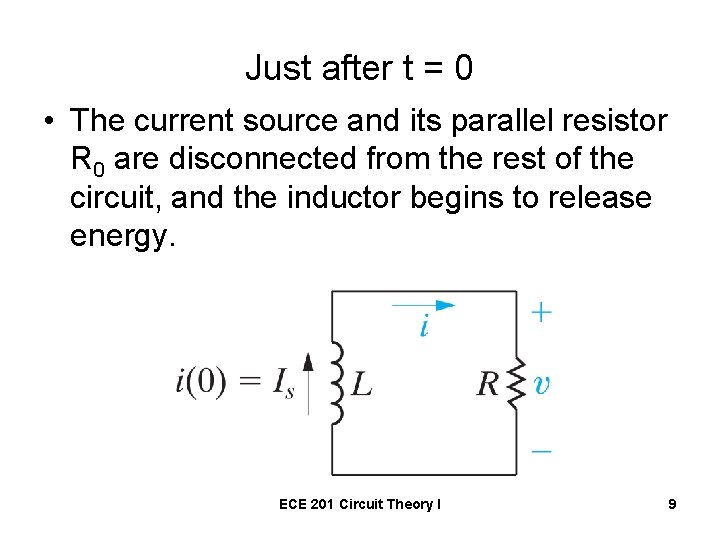
Just after t = 0 • The current source and its parallel resistor R 0 are disconnected from the rest of the circuit, and the inductor begins to release energy. ECE 201 Circuit Theory I 9

The expression for the current ECE 201 Circuit Theory I 10

A first-order ordinary differential equation with constant coefficients. How do we solve it? ECE 201 Circuit Theory I 11
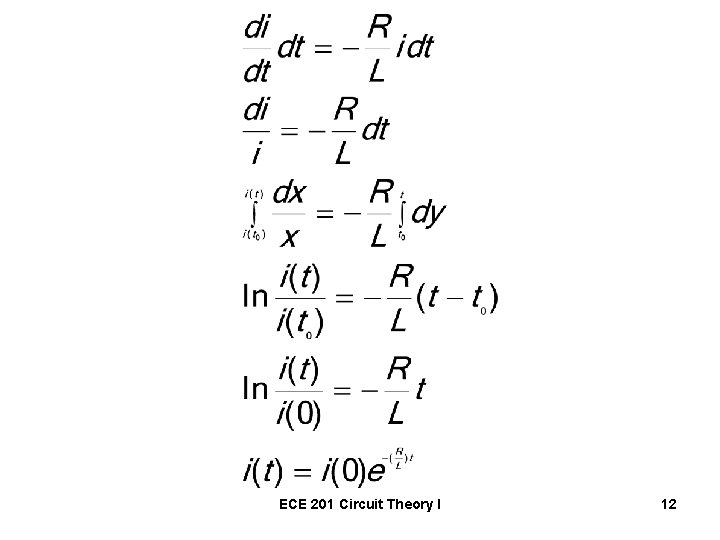
ECE 201 Circuit Theory I 12

The current in an inductor cannot change instantaneously • Let the time just before switching be called t(0 -). • The time just after switching will be called t(0+). • For the inductor, ECE 201 Circuit Theory I 13

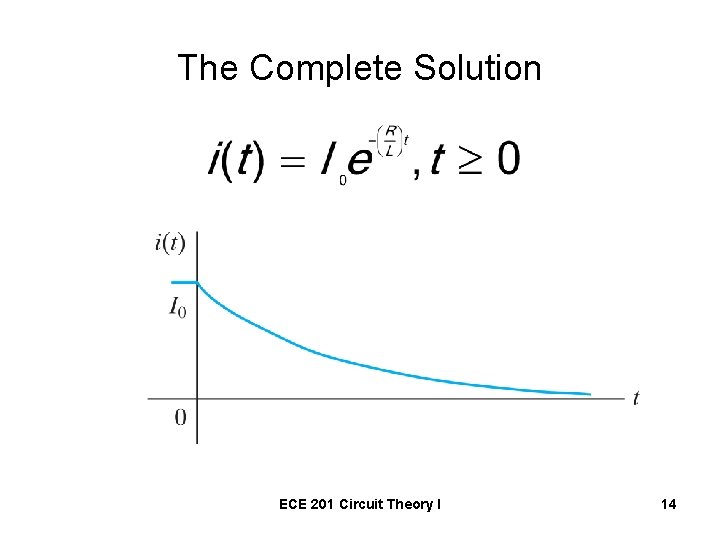
The Complete Solution ECE 201 Circuit Theory I 14

The voltage drop across the resistor ECE 201 Circuit Theory I 15

The Power Dissipated in the Resistor ECE 201 Circuit Theory I 16

The Energy Delivered to the Resistor ECE 201 Circuit Theory I 17

Time Constant • The rate at which the current or voltage approaches zero. ECE 201 Circuit Theory I 18
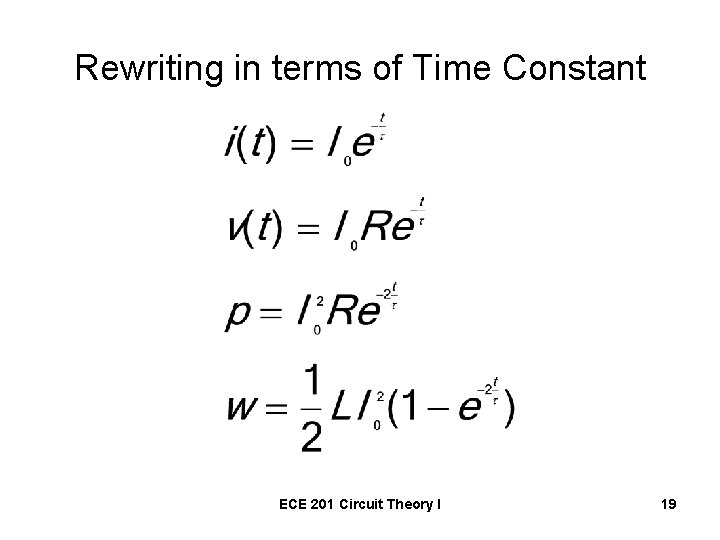
Rewriting in terms of Time Constant ECE 201 Circuit Theory I 19

Table 7. 1 page 217 of the text ECE 201 Circuit Theory I 20

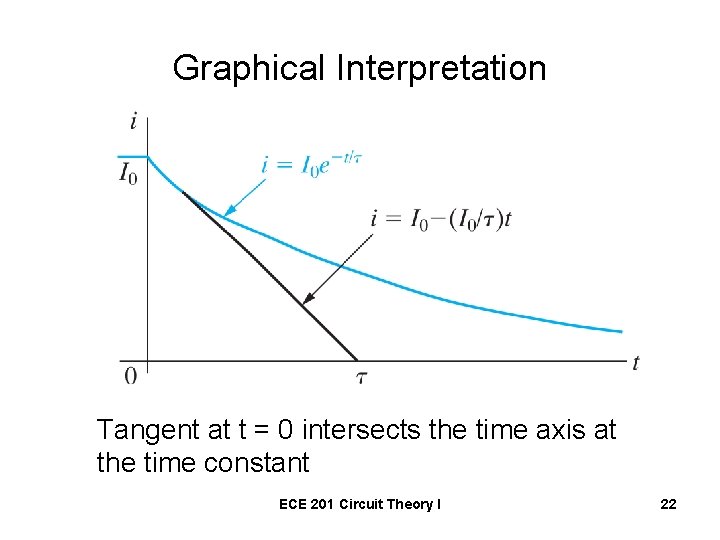
Graphical Interpretation of Time Constant • Determine the time constant from the plot of the circuit’s natural response. Straight Line Approximation ECE 201 Circuit Theory I 21

Graphical Interpretation Tangent at t = 0 intersects the time axis at the time constant ECE 201 Circuit Theory I 22

Procedure to Determine the Natural Response of an RL Circuit • Find the initial current through the inductor. • Find the time constant, τ, of the circuit (L/R). • Generate i(t) from I 0 and τ using ECE 201 Circuit Theory I 23
 Advantages of parallel circuit over series circuit
Advantages of parallel circuit over series circuit First-order circuits
First-order circuits Natural response and forced response
Natural response and forced response Natural response circuit
Natural response circuit Primary immune response and secondary immune response
Primary immune response and secondary immune response Electric circuits grade 6
Electric circuits grade 6 Lesson 8 comparing series and parallel rlc circuits
Lesson 8 comparing series and parallel rlc circuits Circuits activator answer key
Circuits activator answer key Electromotive force and circuits
Electromotive force and circuits The laplace transform in circuit analysis
The laplace transform in circuit analysis Jan m rabaey digital integrated circuits
Jan m rabaey digital integrated circuits Clamping diode circuit
Clamping diode circuit Electric circuits equations
Electric circuits equations Ap physics circuit practice problems
Ap physics circuit practice problems Frequency selective circuit
Frequency selective circuit Microelectronic circuits
Microelectronic circuits Types of elements in electrical circuits
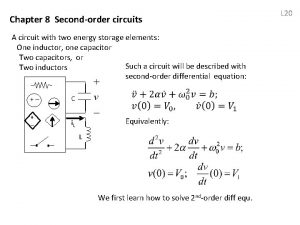
Types of elements in electrical circuits The circuit chapter 8
The circuit chapter 8 Babinski sign
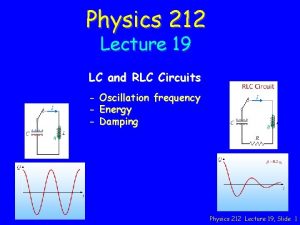
Babinski sign Rc rl lc rlc circuits
Rc rl lc rlc circuits 14-13
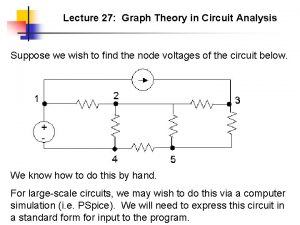
14-13 Solving circuits using graph theory
Solving circuits using graph theory Discrete math circuits
Discrete math circuits First and second order circuits
First and second order circuits