Propositional logic versus firstorder logic Apply firstorder logic

知識表現 推理 • Propositional logic versus first-order logic (命題論理対一階述語論理 ) • Apply first-order logic e. g. A family relations A proof 1

Sentence in propositional logic • Sentence Atomic. Sentence | Complex. Sentence • Atomic. Sentence proposition symbols like P, Q, R 原子文 True | False • Complex. Sentence (Sentence) 複文 | Sentence Connectives like P Q (P Q) ( P Q) 連結語 True | False • Connectives: (not), (and), (or), (implies), and (equivalent) (必然的に）伴う 2

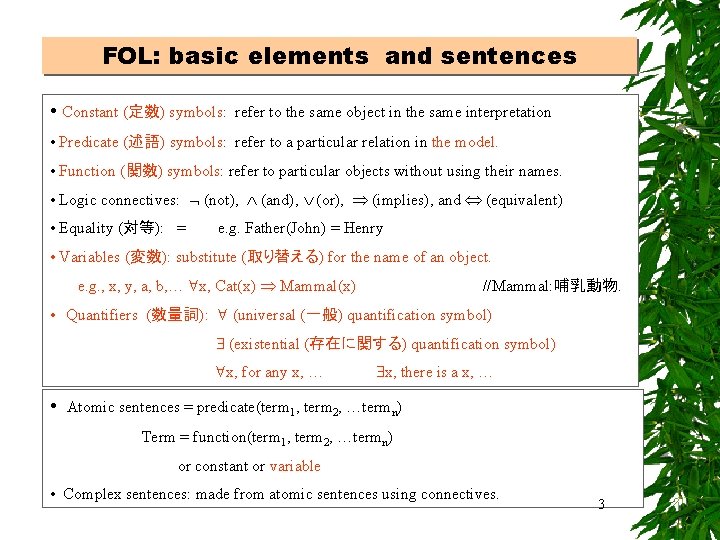
FOL: basic elements and sentences • Constant (定数) symbols: refer to the same object in the same interpretation • Predicate (述語) symbols: refer to a particular relation in the model. • Function (関数) symbols: refer to particular objects without using their names. • Logic connectives: (not), (and), (or), (implies), and (equivalent) • Equality (対等): = e. g. Father(John) = Henry • Variables (変数): substitute (取り替える) for the name of an object. e. g. , x, y, a, b, … x, Cat(x) Mammal(x) //Mammal: 哺乳動物. • Quantifiers (数量詞): (universal (一般) quantification symbol) (existential (存在に関する) quantification symbol) x, for any x, … • x, there is a x, … Atomic sentences = predicate(term 1, term 2, …termn) Term = function(term 1, term 2, …termn) or constant or variable • Complex sentences: made from atomic sentences using connectives. 3

Seven inference rules for propositional Logic • R(1) Implication-Elimination , • R(2) And-Elimination 1 2 … n • R(3) And-Introduction 1, 2, …, n 1 2 … n • R(4) Or-Introduction i 1 2 … n i • R(5) Double-Negation Elimination • R(6) Unit Resolution , • R(7) Logic connectives: , 4

The three new inference rules added to FOL • R(8) Universal-Elimination: For any sentence , variable v, and ground term g: v Ground term is a term that contains no variables. SUBST({v/g}, ) e. g. , x Likes(x, Ice. Cream), we can use the substitute {x/Rose} and infer Like(Rose, Ice. Cream). v/g • R(9) Existential-Elimination: For any sentence , variable v, and constant symbol k that does not appear elsewhere in the knowledge base: v SUBST({v/k}, ) k e. g. , x Kill(x, Victim), we can infer Kill(Murderer, Victim), as long as Murderer does not appear elsewhere in the knowledge base. • R(10) Existential-Introduction: For any sentence , variable v that does not occur in , and ground term g that does occur in : e. g. , from Likes(Rose, Ice. Cream) we can infer x Likes(x, Ice. Cream). v SUBST({g/v}, ) 5

Representing Simple Rules Variables: x, P, C, . . . Generalised Facts: female(P), parent(P, C), . . . Conjunctions: parent(P, C) female(P) Rules: P, C parent(P, C) female(P) mother(P, C) 6

Knowledge Bases: Rules Family Relations GP, P, C parent(P, C) female(P) mother(P, C) parent(P, C) male(P) father(P, C) parent(GP, P) parent(P, C) grandparent(GP, C) parent(GP, P) female(GP) parent(P, C) grandmother(GP, C) grandparent(GP, C) male(GP) grandfather(GP, C) 7

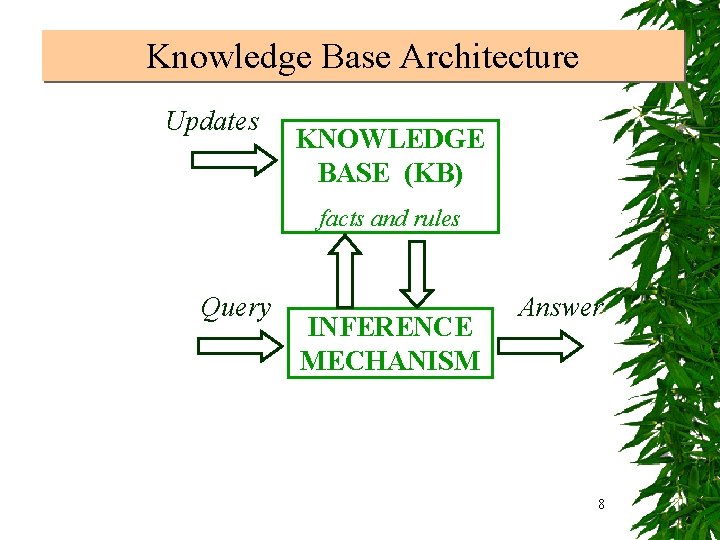
Knowledge Base Architecture Updates KNOWLEDGE BASE (KB) facts and rules Query INFERENCE MECHANISM Answer 8

Example of proof in first-order logic Bob is a buffalo | 1. Buffalo(Bob) --f 1 Pat is a pig | 2. Pig(Pat) --f 2 Buffaloes run faster than pigs | 3. x, y Buffalo(x) Pig(y) Faster(x, y) --r 1 --------------------------------------------------To proof: Bob runs faster than Pat -------------------------------------------------Apply R(3) to f 1 And f 2 | 4. Buffalo(Bob) Pig(Pat) --f 3 (And-Introduction) Apply R(8) to r 1 {x/Bob, y/Pat} | 5. Buffalo(Bob) Pig(Pat) Faster(Bob, Pat) --f 4 (Universal-Elimination) Apply R(1) to f 3 And f 4 (Inplication-Elimination ) | 6. Faster(Bob, Pat) --f 5 9

Search with primitive inference rules Operators are inference rules States are sets of sentences Goal test checks state to see if it contains query sentence R(1) to R(10) are common inference pattern 123 Apply R(3) to 1 & 2 1234 Apply R(8) to 3 12345 Apply R(1) to 4 & 5 123456 10

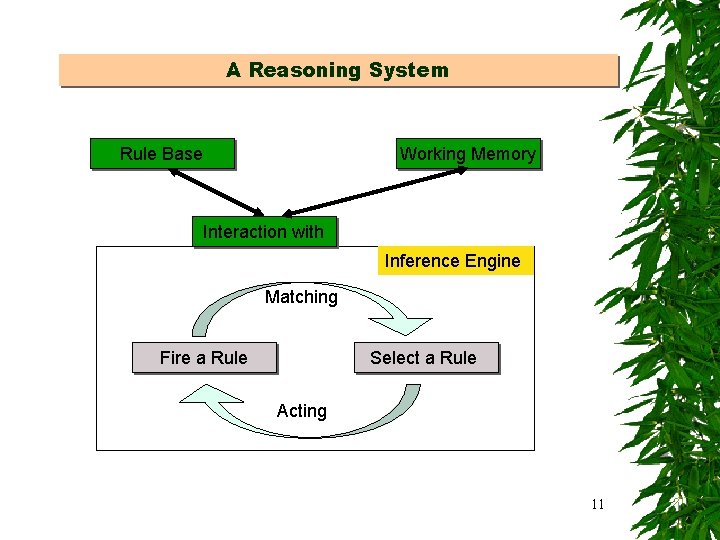
A Reasoning System Rule Base Working Memory Interaction with Inference Engine Matching Fire a Rule Select a Rule Acting 11

Finding gold The agent has been in [1, 1]->[2, 1]->[1, 2] and knows there is a wumpus in [1, 3] and a pit in [3, 1] then goes to [2, 2] continues to [3, 2] (forward since it perceives nothing special) Now, percept sentences (add a new one): there is a breeze in the square [3, 2] B 3, 2 Since knowledge is not enough to judge whether [4, 2] and [3, 3] are safe or not, the agent goes back to [2, 2], turn left and goes to [2, 3]. Now, percept sentences(add new ones): there is a glitter in the square [2, 3] G 2, 3 The agent has been in [1, 1]->[2, 1]->[1, 2] -> [2, 2] -> [3, 2] -> [2, 2]-> [2, 3] Here is the answer: the gold is in [2, 3]. 12

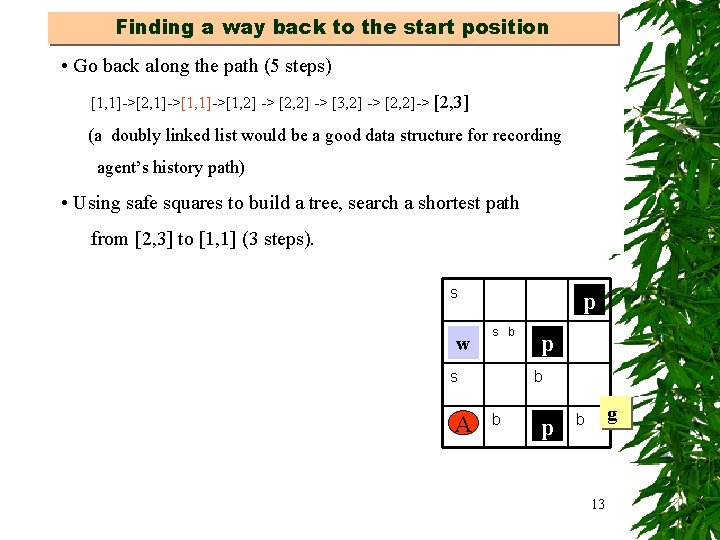
Finding a way back to the start position • Go back along the path (5 steps) [1, 1]->[2, 1]->[1, 2] -> [2, 2] -> [3, 2] -> [2, 2]-> [2, 3] (a doubly linked list would be a good data structure for recording agent’s history path) • Using safe squares to build a tree, search a shortest path from [2, 3] to [1, 1] (3 steps). s w p s b s A p b b p g b 13

Appendix (追加) Apply first-order logic to making inference in the Wumpus world. (If you have time, please take a look this appendix. ) A gold finding agent in the Wumpus world 14

• Predicates and rules At(p, l, S) : Agent p is at the location l in the situation S Percept([Smell, b, g, u, v], l, S, t): Agent perceives smell at time t at the location l in the situation S • Perception rules R 1: b, g, u, v, l, s, t Percept([Smell, b, g, u, v], s, t) Smell(t) R 2: sm, g, u, v, l, s, t Percept([sm, Breeze, g, u, v], s, t) Breeze(t) R 3: sm, b, u, v, l, s, t Percept([sm, b, Glitter, u, v], s, t) At. Gold. Room(t) R 4: sm, b, u, v, l, s, t Percept([sm, b, g, Wall, v], s, t) Wall(t) R 6: sm, b, g, u, v, l, s, t Percept([sm, b, g, u, v], s, t) Smell(t) Breeze(t) At. Gold. Room(t) Wall(t) • Action rules R 7: i, j Result(Forward, li) = lj i j l i, j Result(Turn, Sm) = Sn m n Orientation rules R 8: s (Orientation(p, s ) =0 Face(p, east) ) (Orientation(p, s) = 90 Face(p, north ) (Orientation(p, s) = 180 Face(p, west) (Orientation(p, s) = 270 Face(p, south) ) R 9: a, d, p, s Orientation(p, Result(a, s)) =d [(a=Turn(Right) d=Mod(Orientation(p, s) – 90, 360)) (a=Turn(Left) d=Mod(Orientation(p, s) + 90, 15 360) ) (Orientation(p, s)=d (a=Turn(Right) a=Turn(Left)))]

• Location rules R 10: l, l x, y [x, y] R 11: (a) x, y Location. Toward([x, y], 0) = [x+1, y] (b) x, y Location. Toward([x, y], 90) = [x, y+1] R 12: (a) x, y Location. Toward([x, y], 180) = [x-1, y] (b) x, y Location. Toward([x, y], 270) = [x+1, y-1] R 13: p, l, s At(p, l, s) Location. Ahead(p, S) = Location. Toward(l, Orientation(p, s)) R 14: l 1, l 2 Adjacent(l 1, l 2) d l 1=Location. Toward(l 2, d) R 15: x, y Wall([x, y]) (x=0 x=5 y=0 y=5) R 16: a, d, p, s At(p, l, Result(a, s)) [(a=Forward l = Location. Ahead(p, s) Wall(l)) (At(p, l, s) a Forward)] • Hidden properties (rules) R 17: l, s At(Agent, l, s) Smell(l) R 18: l, s At(Agent, l, s) Breeze(l) R 19: l 1, s Breeze(l 1) l 2 At(Pit, l 2, s) (l 2, = l 1 Adjacent(, l 1, l 2)) R 20: l 1, l 2, s At(Pit, l 1) Adjacent(, l 1, l 2) Breeze(l 2) R 21: l 1, s Breeze(l 1) l 2 At(Pit, l 2, s ) (l 2, = l 1 Adjacent(, l 1, l 2)) 16

• Hidden properties (rules) R 22: l 1, s Smell(l 1) l 2 At(Wumpus, l 2, s) (l 2, = l 1 Adjacent(, l 1, l 2)) R 23: l 1, l 2, s At(Wumpus, l 1) Adjacent(, l 1, l 2) Smell(l 2) R 24: l 1, s Smell(l 1) l 2 At(Wumpus, l 2, s ) (l 2, = l 1 Adjacent(, l 1, l 2)) R 25: x, y, g, u, v, s, t Percept([None, g, u, v], t) At(Agent, x, s) Adjacent(, x, y) OK(y) R 26: x, t ( At(Wumpus, x, t) At(Pit, x, t)) OK(x) • Obtaining Gold R 27: x, s At. Gold. Room( x, s) Present(Gold, x, s) R 28: x, s Present( x, s) Portable(x) Holding(x, Result(Grab, s)) R 29: x, s Holding(x, Result(Release, s)) R 30: a, x, s Holding(x, s) (a Release) Holding(x, Result(a, s)) R 31: a, x, s Holding(x, s) (a Grab (Present(x, s) Portable(x)) Holding(x, Result(a, s)) P true afterwards [an action made P true already and no action made P false] R 32: a, x, s Holding(x, Result(a, s)) 17 [(a=Grab (Present(x, s) Portable(x)) (Holding(x, s) a Release) ]

Since the world is not changing, our inferences below drop time term. Initial state At(Agent, [1, 1]) Apply And-Elimination rule to R 6, we obtain C 1 Smell([1, 1]) , Breeze([1, 1]) , At. Gold. Room([1, 1]) , Wall([1, 1]) Apply And-Elimination rule to R 21 and apply R 15, we obtain C 2 At(Pit, [1, 1]), At(Pit, [2, 1]), Wall([1, 0]), Wall([0, 1]) Apply And-Elimination rule to R 24, we obtain C 3 At(Wumpus, [1, 1]), At(Wumpus, [2, 1]), At(Wumpus, [1, 2]) Apply R 26 to C 2 and C 3, we obtain C 4 OK([1, 1]), OK([2, 1]), OK([1, 2]) Apply R 11(a) and R 16, we obtain At(Agent, [2, 1]) Apply And-Elimination rule to R 2, we obtain C 5 Smell([2, 1]) , Breeze([2, 1]) , At. Gold. Room([2, 1]) , Wall([2, 1]) Apply R 19 to Breeze([2, 1]), we obtain C 6 At(Pit, [1, 1]) At(Pit, [2, 2]) At(Pit, [3, 1]) 18

Apply unit resolution twice to C 6, we obtain C 7 At(Pit, [2, 2]) At(Pit, [3, 1]) Use C 4 and C 7, (for a conservative agent, it would not go where is not sure), and apply R 9, R 12(a) and R 16, we obtain At(Agent, [1, 1]), Orientation(Agent, [1, 1])=180 Use C 4 and apply R 9, R 11(b) and R 16, we obtain At(Agent, [1, 2]), Orientation(Agent, [1, 2])=90 Apply R 22 to Smell([1, 2]), we obtain C 8 At(Wumpus, [1, 1]) At(Wumpus, [1, 3]) At(Wumpus, [1, 2]) At(Wumpus, [2, 2]) Apply unit resolution twice to C 8, we obtain C 9 At(Wumpus, [2, 2]) At(Wumpus, [1, 3]) Apply R 24 and And-Elimination rule to Smell([2, 1]), we obtain C 10 At(Wumpus, [1, 1]), At(Wumpus, [1, 2]), At(Wumpus, [2, 1]) Apply unit resolution to C 9, we obtain C 11 At(Wumpus, [1, 3]) Apply R 21 and And-Eleimination rule to Breeze([1, 2]), we obtain C 12 At(Pit, [1, 1]), At(Pit, [2, 2]), At(Pit, [3, 1]) 19

Apply R 26 to C 10 and C 12, we obtain C 13 OK([2, 2]), Use C 13 and apply R 9, R 11(a) and R 16, we obtain At(Agent, [2, 2]), Orientation(Agent, [2, 2])=0 Use C 4 and apply R 9, R 11(b) and R 16, we obtain At(Agent, [1, 2]), Orientation(Agent, [1, 2])=90 Apply R 21 and And-Elimination rule to Breeze([2, 2]), and apply R 24 and And-Elimination rule to Smell([2, 2]), we obtain C 14 At(Pit, [2, 1]), At(Pit, [1, 2]), At(Pit, [2, 3], At(Pit, [2, 3]) C 15 At(Wumpus, [2, 1]), At(Wumpus, [1, 2]), At(Wumpus, [2, 3], At(Wumpus, [3, 2]) Apply R 26 to C 14 and C 15, we obtain C 16 OK([2, 3]), OK([3, 2]) Apply R 11(a) and R 16, we obtain At(Agent, [3, 2]) Apply R 19 to Breeze([3, 2]), we obtain C 17 At(Pit, [2, 2]) At(Pit, [2, 3]) At(Pit, [3, 2]) At(Pit, [3, 1]) At(Pit, [4, 2]) Apply twice unit resolution to C 9, we obtain C 18 At(Pit, [3, 2]) At(Pit, [3, 1]) At(Pit, [4, 2]) 20

For safe, agent goes back to [2, 2] Use C 13 and apply R 9, R 12(a) and R 16, we obtain At(Agent, [2, 2]), Orientation(Agent, [2, 2])=180 Use C 16 and apply R 9, R 11(b) and R 16, we obtain At(Agent, [2, 3]), Orientation(Agent, [2, 3])=90 Apply R 3, we obtain C 19 At. Gold. Room( [2, 3]) Apply R 32, we obtain C 20 Holding([2, 3], Result(Grab)) The rest of question is how to go back safely? 21