Lecture 18 Review First order circuit natural response

Lecture 18 • Review: • First order circuit natural response • Forced response of first order circuits • Step response of first order circuits • Examples • Related educational materials: –Chapter 7. 4, 7. 5

Natural response of first order circuits – review • Circuit being analyzed has a single equivalent energy storage element • Circuit being analyzed is “source free” • Any sources are isolated from the circuit during the time when circuit response is determined • Circuit response is due to initial energy storage • Circuit response decays to zero as t

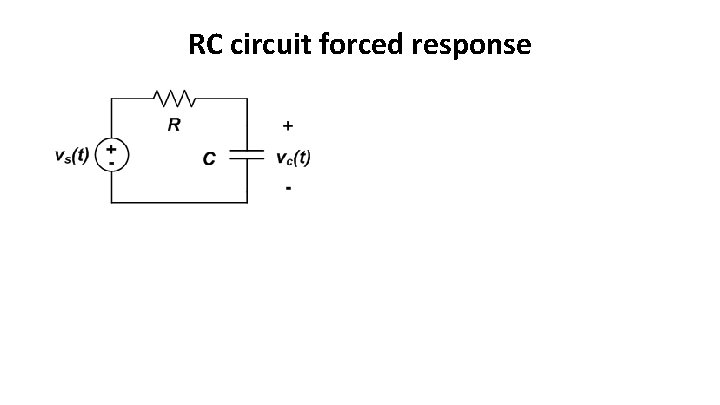
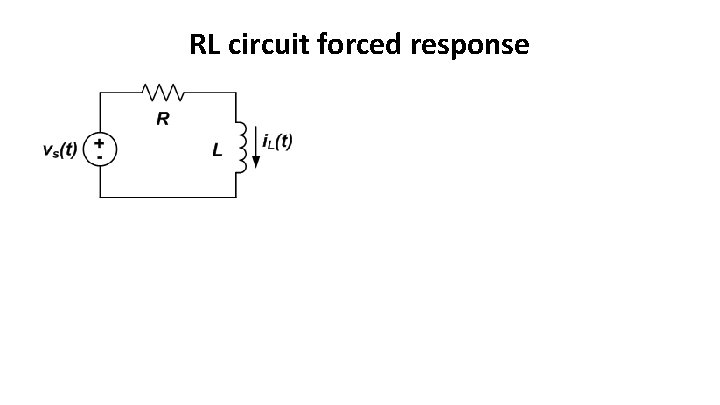
First order circuit forced response – overview • Now consider the response of circuits with sources • Notes: • We will typically write our equations in terms of currents through inductors and voltages across capacitors • The above circuits are very general; consider them to be the Thévenin equivalent of a more complex circuit

RC circuit forced response

RL circuit forced response

First order circuit forced response – summary • Forced RC circuit response: • Forced RL circuit response:

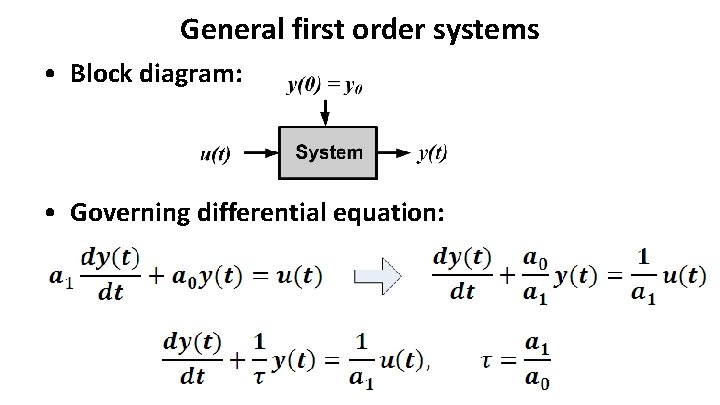
General first order systems • Block diagram: • Governing differential equation:

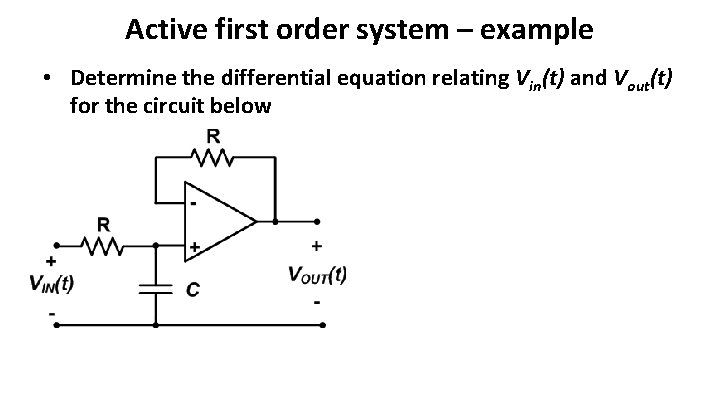
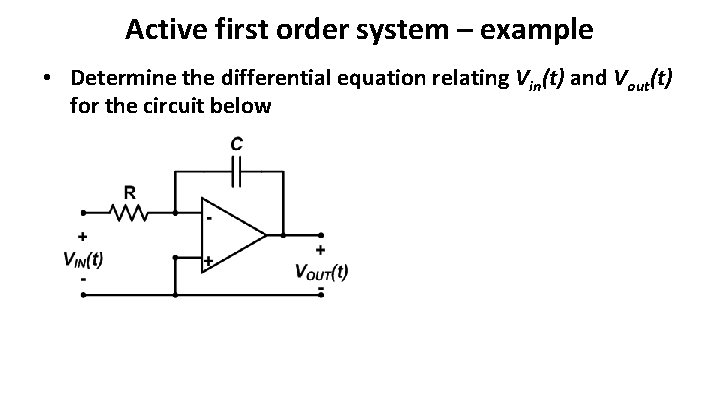
Active first order system – example • Determine the differential equation relating Vin(t) and Vout(t) for the circuit below

Active first order system – example • Determine the differential equation relating Vin(t) and Vout(t) for the circuit below

Step Response – introduction • Our previous results are valid for any forcing function, u(t) • In this course, we will be mostly concerned with a couple of specific forcing functions: • Step inputs • Sinusoidal inputs • We will defer our discussion of sinusoidal inputs until later

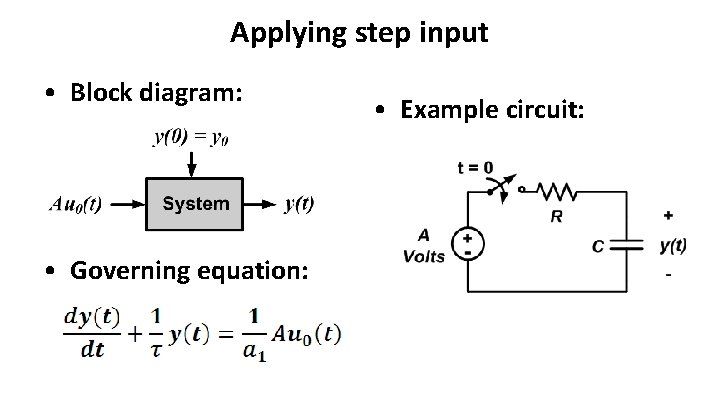
Applying step input • Block diagram: • Governing equation: • Example circuit:

First order system step response • Solution is of the form: • yh(t) is homogeneous solution • Due to the system’s response to initial conditions • yh(t) 0 as t • yp(t) is the particular solution • Due to the particular forcing function, u(t), applied to the system • y (t) yp(t) as t

First order system – homogeneous solution • Assume form of solution: • Substitute into homogeneous D. E. and solve for s : • Homogeneous solution:

First order system – particular solution • Recall that the particular solution must: 1. Satisfy the original differential equation as t 2. Have the same form as the forcing function • As t :

First order system particular solution -- continued • As t , the original differential equation becomes: • The particular solution is then

First order system step response • Superimpose the homogeneous and particular solutions: • Substituting our previous results: • K 1 and K 2 are determined from initial conditions and steady-state response; is a property of the circuit

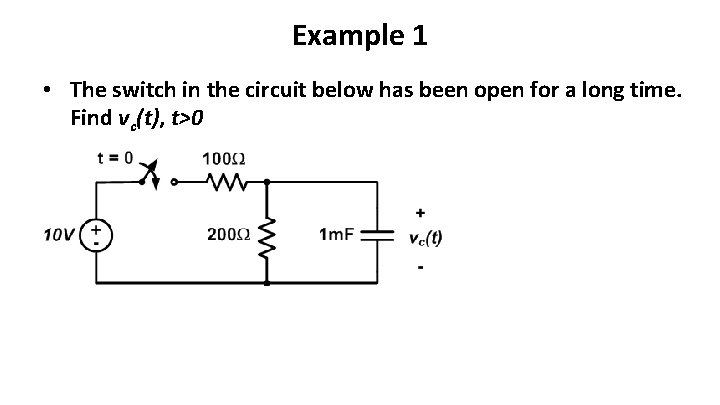
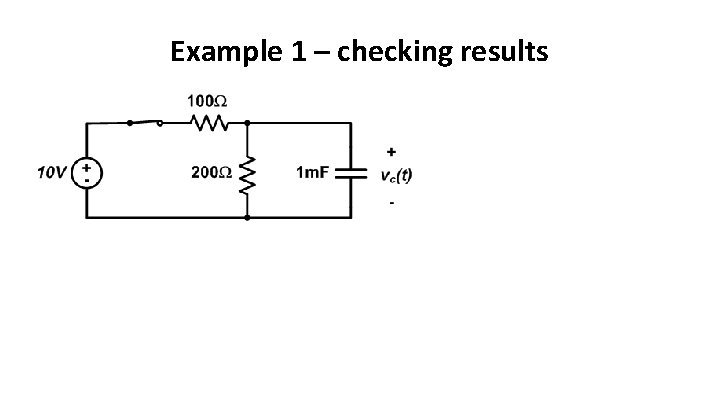
Example 1 • The switch in the circuit below has been open for a long time. Find vc(t), t>0

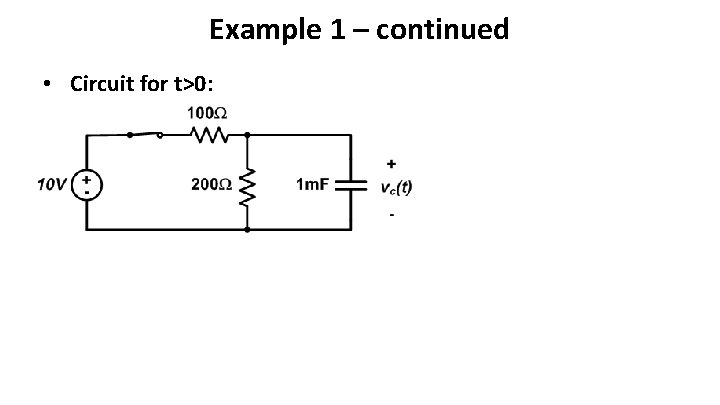
Example 1 – continued • Circuit for t>0:

Example 1 – continued again • Apply initial and final conditions to determine K 1 and K 2 Governing equation: Form of solution:

Example 1 – checking results