Response of FirstOrder Circuits RL Circuits RC Circuits





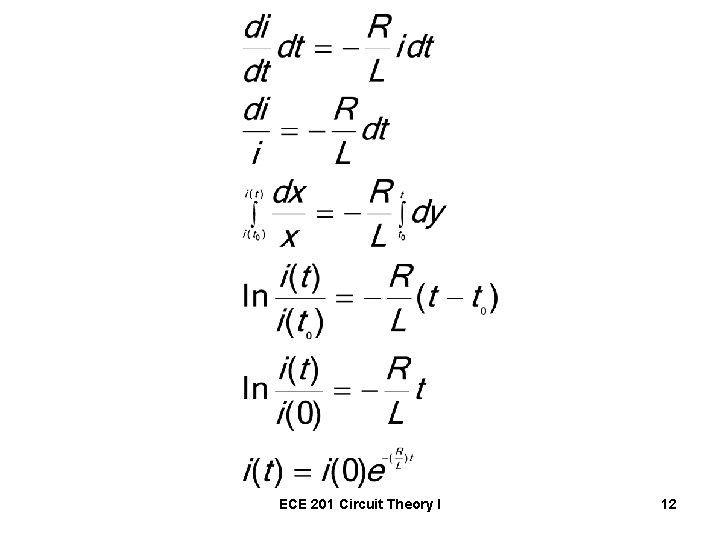





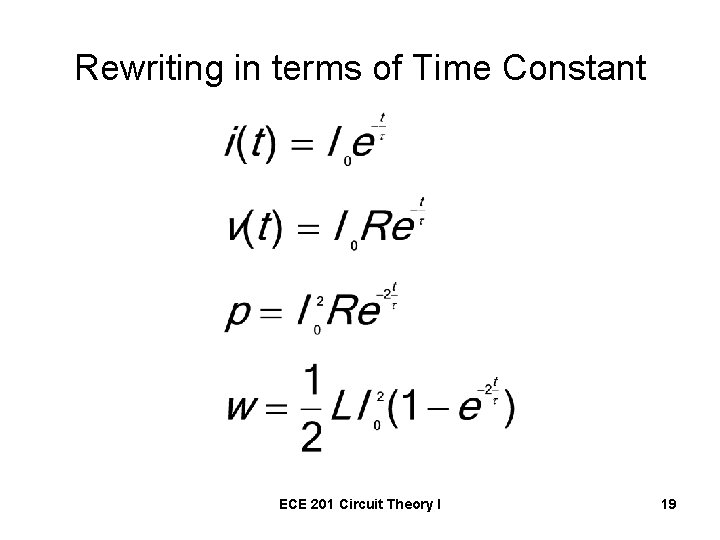



- Slides: 23

Response of First-Order Circuits RL Circuits RC Circuits ECE 201 Circuit Theory I 1

The Natural Response of a Circuit • The currents and voltages that arise when energy stored in an inductor or capacitor is suddenly released into a resistive circuit. • These “signals” are determined by the circuit itself, not by external sources! ECE 201 Circuit Theory I 2

Step Response • The sudden application of a DC voltage or current source is referred to as a “step”. • The step response consists of the voltages and currents that arise when energy is being absorbed by an inductor or capacitor. ECE 201 Circuit Theory I 3

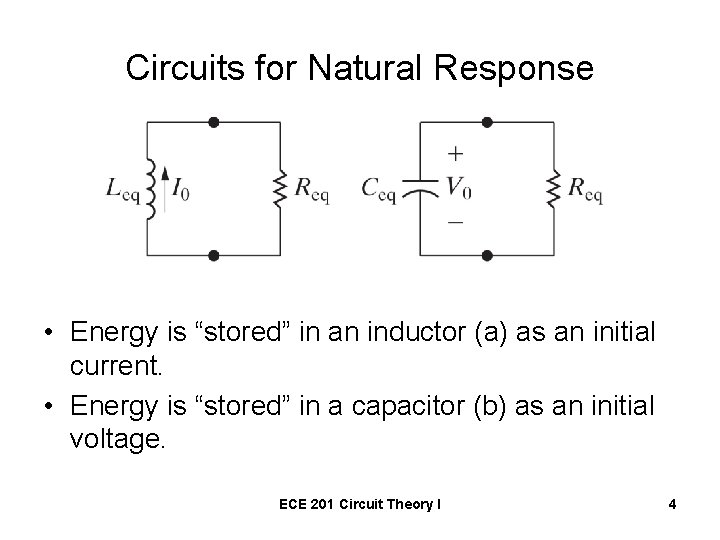
Circuits for Natural Response • Energy is “stored” in an inductor (a) as an initial current. • Energy is “stored” in a capacitor (b) as an initial voltage. ECE 201 Circuit Theory I 4

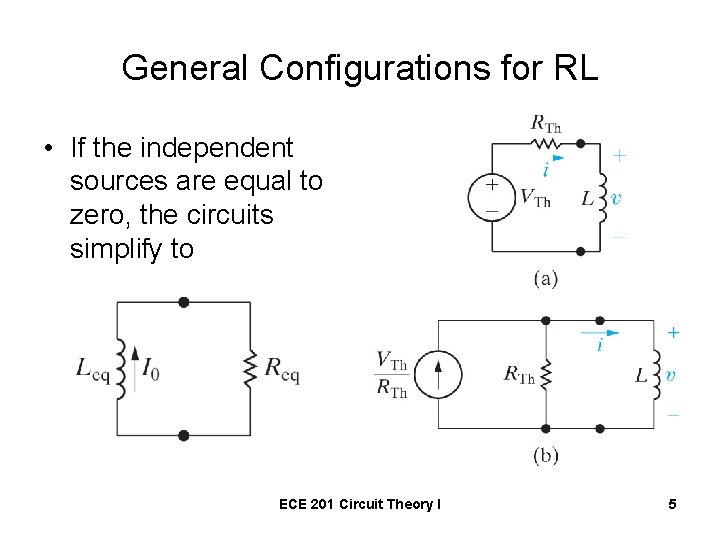
General Configurations for RL • If the independent sources are equal to zero, the circuits simplify to ECE 201 Circuit Theory I 5

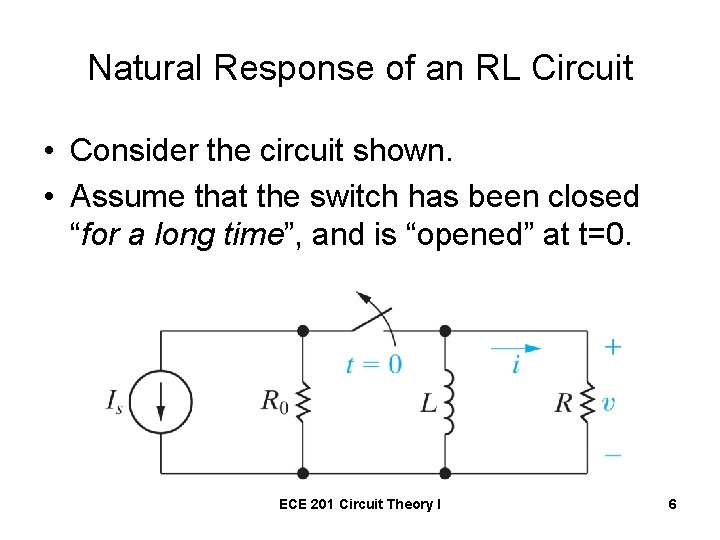
Natural Response of an RL Circuit • Consider the circuit shown. • Assume that the switch has been closed “for a long time”, and is “opened” at t=0. ECE 201 Circuit Theory I 6

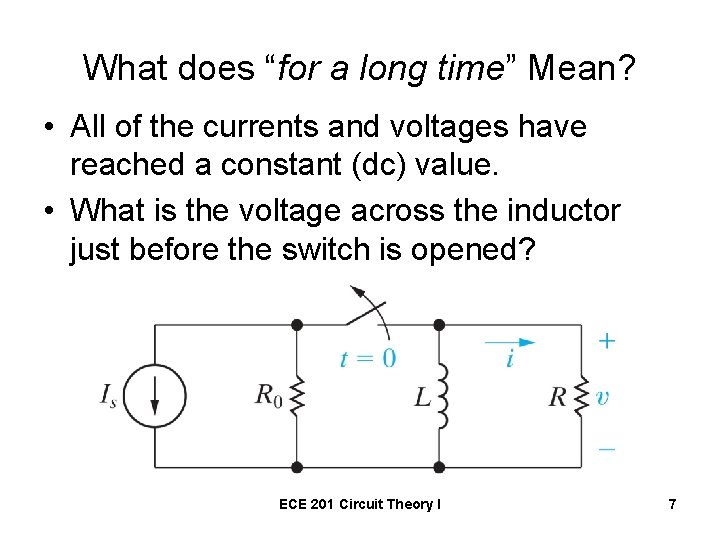
What does “for a long time” Mean? • All of the currents and voltages have reached a constant (dc) value. • What is the voltage across the inductor just before the switch is opened? ECE 201 Circuit Theory I 7

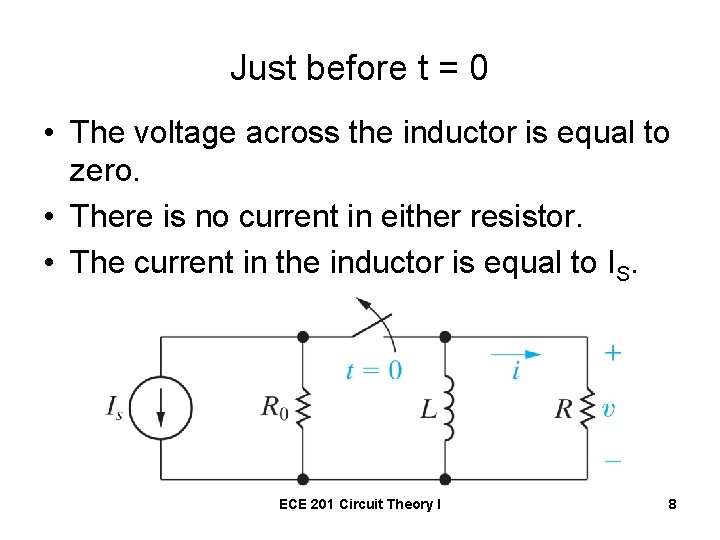
Just before t = 0 • The voltage across the inductor is equal to zero. • There is no current in either resistor. • The current in the inductor is equal to IS. ECE 201 Circuit Theory I 8

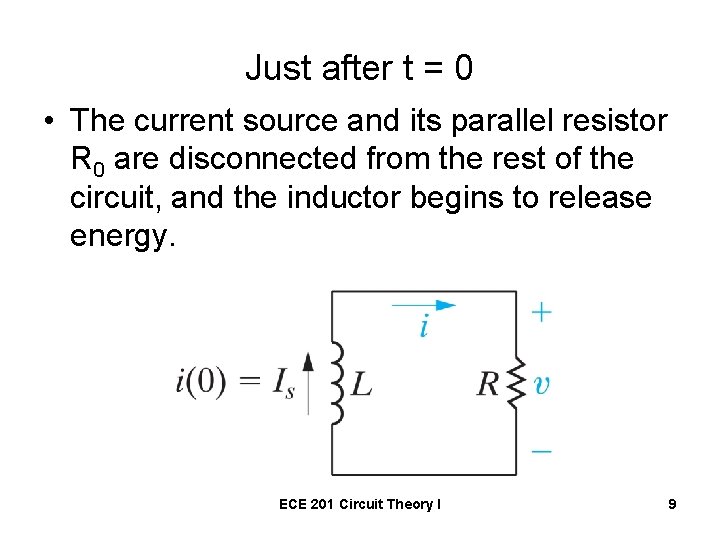
Just after t = 0 • The current source and its parallel resistor R 0 are disconnected from the rest of the circuit, and the inductor begins to release energy. ECE 201 Circuit Theory I 9

The expression for the current ECE 201 Circuit Theory I 10

A first-order ordinary differential equation with constant coefficients. How do we solve it? ECE 201 Circuit Theory I 11
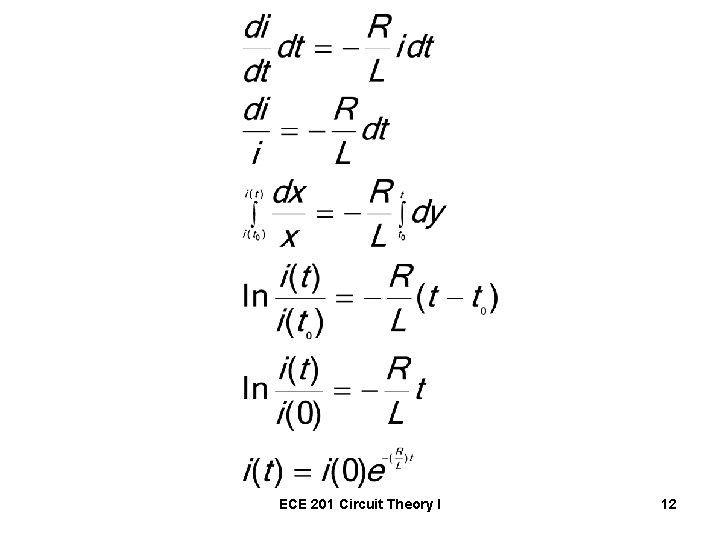
ECE 201 Circuit Theory I 12

The current in an inductor cannot change instantaneously • Let the time just before switching be called t(0 -). • The time just after switching will be called t(0+). • For the inductor, ECE 201 Circuit Theory I 13

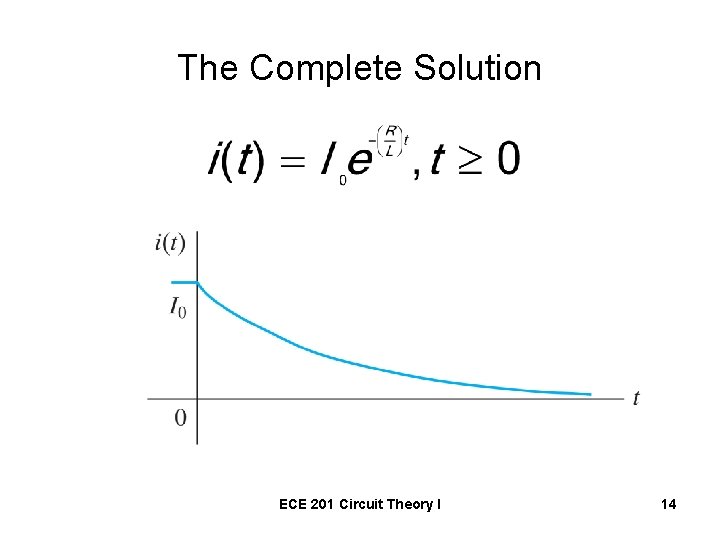
The Complete Solution ECE 201 Circuit Theory I 14

The voltage drop across the resistor ECE 201 Circuit Theory I 15

The Power Dissipated in the Resistor ECE 201 Circuit Theory I 16

The Energy Delivered to the Resistor ECE 201 Circuit Theory I 17

Time Constant • The rate at which the current or voltage approaches zero. ECE 201 Circuit Theory I 18
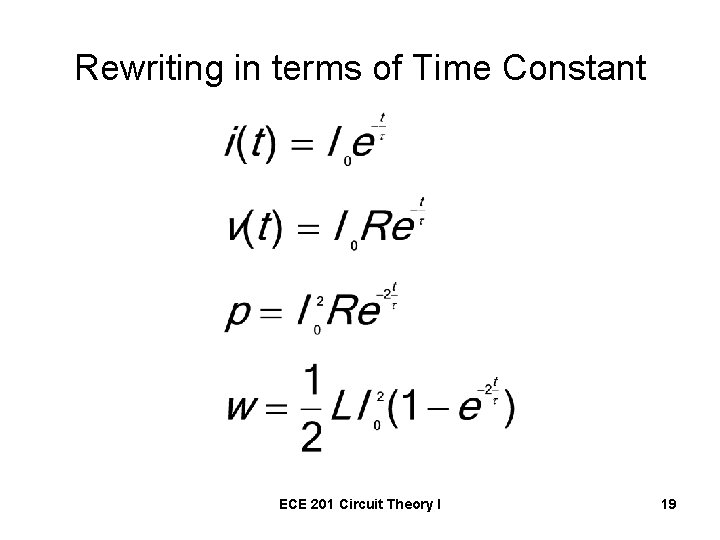
Rewriting in terms of Time Constant ECE 201 Circuit Theory I 19

Table 7. 1 page 233 of the text ECE 201 Circuit Theory I 20

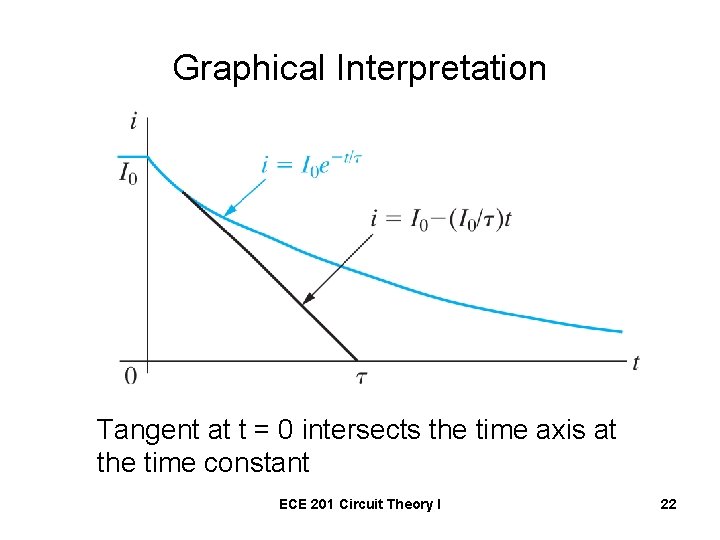
Graphical Interpretation of Time Constant • Determine the time constant from the plot of the circuit’s natural response. Straight Line Approximation ECE 201 Circuit Theory I 21

Graphical Interpretation Tangent at t = 0 intersects the time axis at the time constant ECE 201 Circuit Theory I 22

Procedure to Determine the Natural Response of an RL Circuit • Find the initial current through the inductor. • Find the time constant, τ, of the circuit (L/R). • Generate i(t) from I 0 and τ using ECE 201 Circuit Theory I 23