Industrial Calculations For Transient Heat Conduction P M




















- Slides: 29

Industrial Calculations For Transient Heat Conduction P M V Subbarao Associate Professor Mechanical Engineering Department IIT Delhi Applications where rate/duration of heating/cooling is a Design Parameter……

General Form of Fourier’s Equation Cartesian coordinates: Cylindrical coordinates: Spherical coordinates:

One-dimensional Transient Conduction • One-dimensional transient conduction refers to a case where the temperature varies temporally and in one spatial direction. • For example, temperature varies with x and time. • Three cases of 1 -D conduction are commonly studied: conduction through a plate, in a cylinder, and in a sphere. • In all three cases, the surface of the solid is exposed to convection. • The exact analytical solutions to the three cases are very complicated. • Industry uses an approximate solution, obtained by using graphical tools. • The graphs allow you to find the centerline temperature at any given time, and the temperature at any location based on the centerline temperature.

One Dimensional Fourier’s Equations Constant thermal conductivity & No heat generation: Cartesian coordinates: Cylindrical coordinates: Spherical coordinates:

Primitive Variables & derived Variables Characteristic Space Dimension : L or ro Characterisitc Time Dimension : ? Characteristic Temperature Variables: Initial Temperature : T 0 Far Field Fluid Temperature : T Characterisitc Medium Property : a

Extent of Solution Domain Highest Measure of Excess Temperature : q 0 =|T 0 -T | Instantaneous local Excess temperature: q = |T -T | Cartesian coordinates: Cylindrical coordinates: Spherical coordinates:

Nature of Solution Cartesian coordinates: Cylindrical coordinates: Spherical coordinates:

Dimensional Analysis & Similarity Variables Buckingham Method The Buckingham theorem states that the function relationship among n quantities or variables whose units may be given in terms of m fundamental units or dimensions may be written as (n – m) dimensionless groups. The variables in local instantaneous temperature excess (q) calculation are: q 0, x, L, t, h, k, C and r. Total number of variables : 8 Fundamental variables : 4 Number of non-dimensional variables : 4

Final form of Equations: The π groups must be independent of each other and no one group should be formed by multiplying together powers of other groups. The recurring set must contain three variables that cannot themselves be formed into a dimensionless group. In this case there are two restriction : Both q and q 0 cannot be chosen as they can be formed into a dimensionless group, (q 0/q). Similarly, x and L cannot be chosen.

Heisler Parameters • Heisler divided the problem into two parts. • Part 1 : Instantaneous center line temperature. Variables are q 0, , L, t, and a. • Part 2 : Spatial temperature distribution for a given center line temperature. Variables are : qcenter, , x, L, and a. • • Two different charts were developed. Three parameters are needed to use each of these charts: First Chart : Normalized centerline temperature, the Fourier Number, and the Biot Number. The definition for each parameter are listed below:

Mid Plane Temperature of Slab

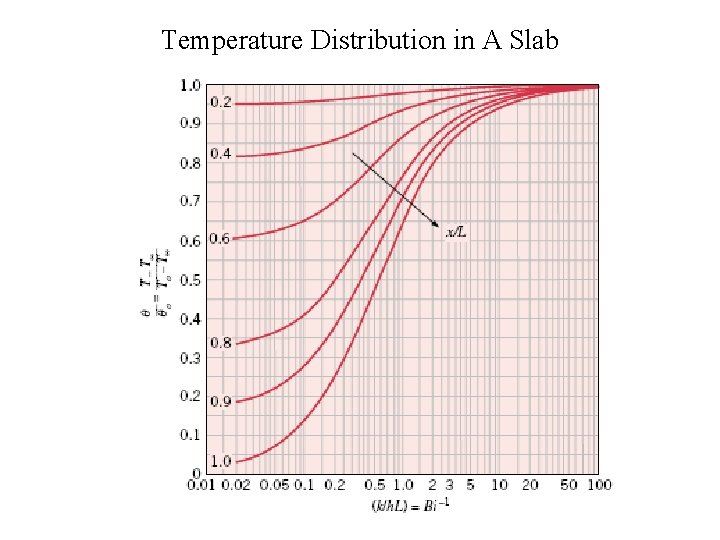
Reading the Graphs • To find the centerline temperature, first calculate Fo and Bi-1. • This chart has Fo on the horizontal axis, θ 0* on the vertical, and lines representing different values of Bi-1. • Locate the line corresponding to the Bi-1 you have calculated. • Next, locate the value of Fo on the x-axis, and draw a vertical line from the axis so that it intersects the Bi-1 line. • From the intersection point, draw a horizontal line. • The value at which the horizontal line crosses the y-axis is the normalized centerline temperature. • To find the temperature at any location within the solid, we now will use the second chart.

Mid Plane Temperature of Slab

Temperature Distribution in A Slab

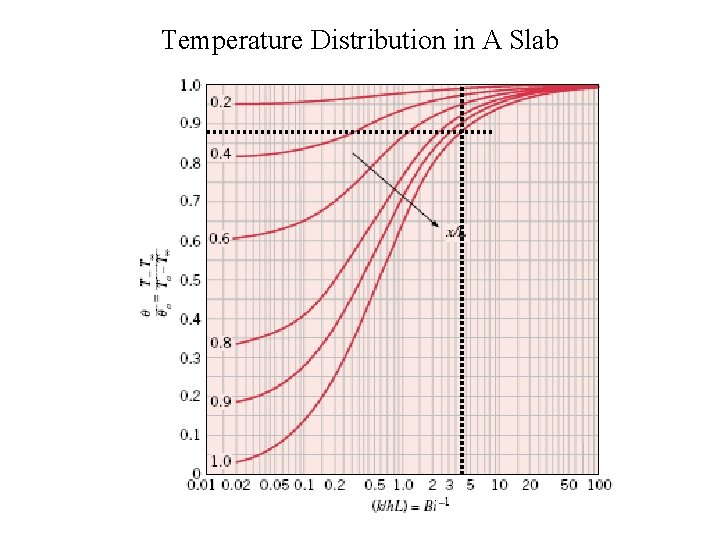
• The second chart has Bi-1 on the horizontal axis, normalized temperature on the vertical axis, and lines corresponding to normalized distance, x/L or r/r 0. • Calculate the normalized distance for the point which you are interested in, and locate the corresponding line on the graph. • Using the calculated value of Bi-1, draw a vertical line through the graph. • Draw a horizontal line from the point of intersection between normalized distance curve and the vertical line. • The point at which the horizontal line intersects the y-axis is the normalized temperature at that location.

Temperature Distribution in A Slab

Change in Internal Energy of A Slab

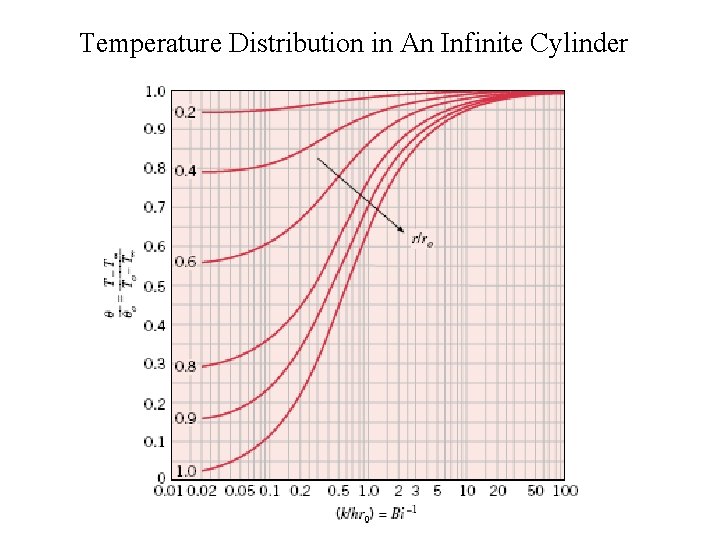
Centre Line Temperature of An Infinite Cylinder

Temperature Distribution in An Infinite Cylinder

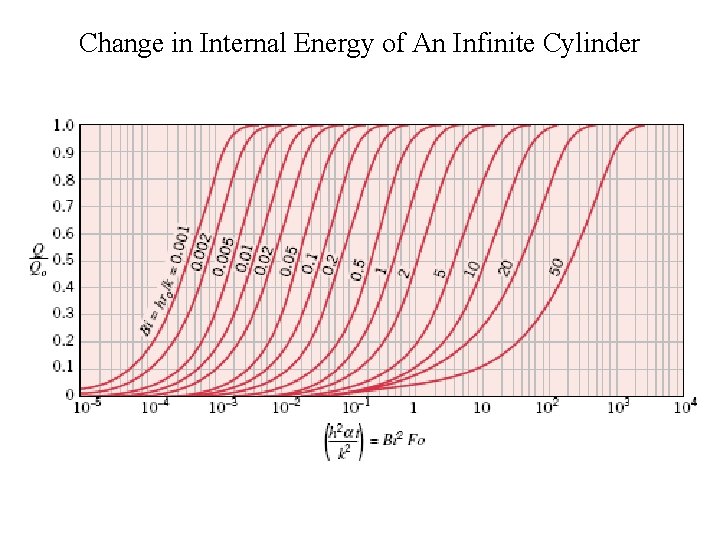
Change in Internal Energy of An Infinite Cylinder

Centre Temperature of A Sphere

Temperature Distribution in A Sphere

Change in Internal Energy of A Sphere

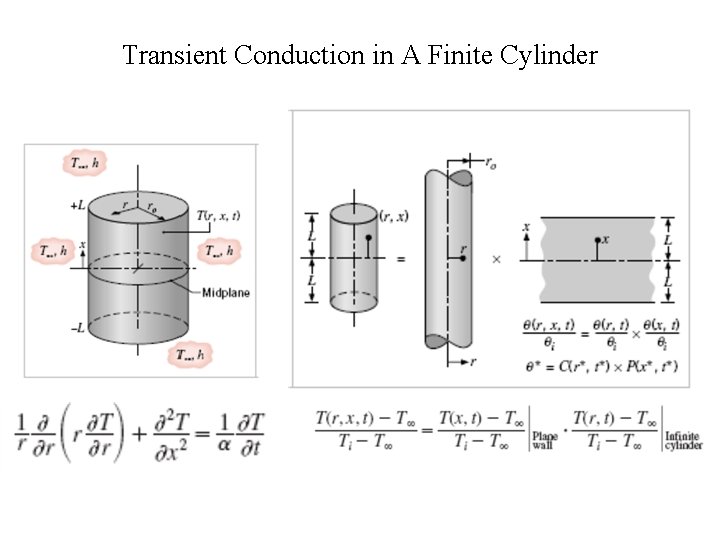
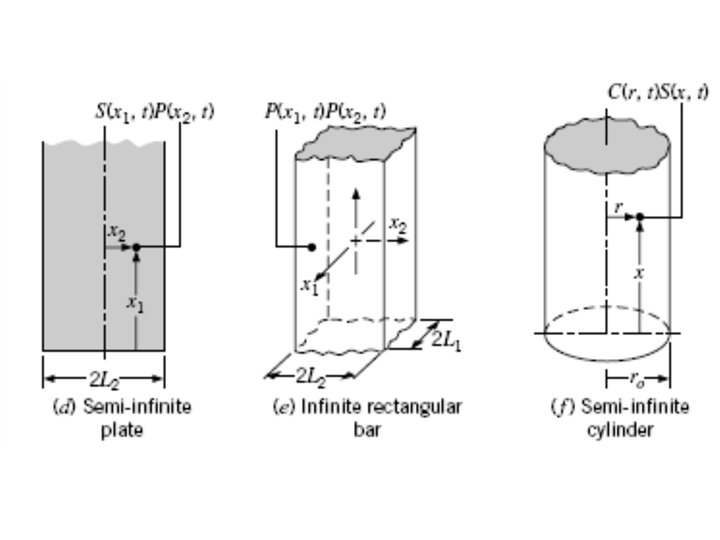
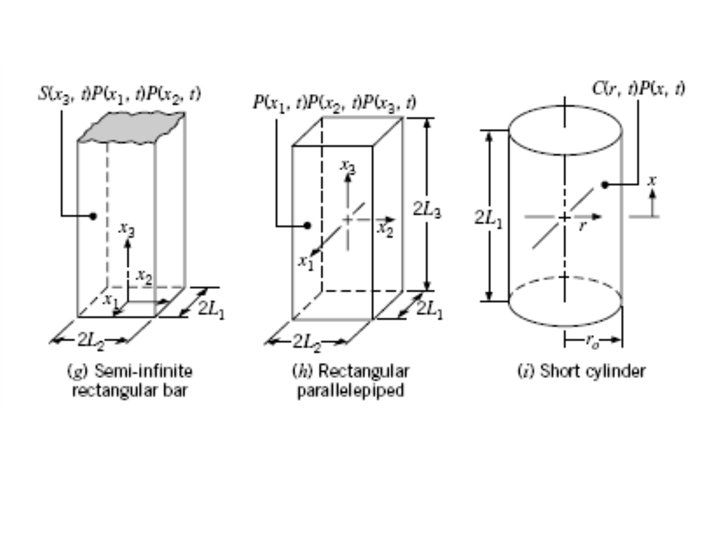
Multi-dimensional Transient Conduction Finite Cartesian Bodies: Finite Cylindrical Bodies:

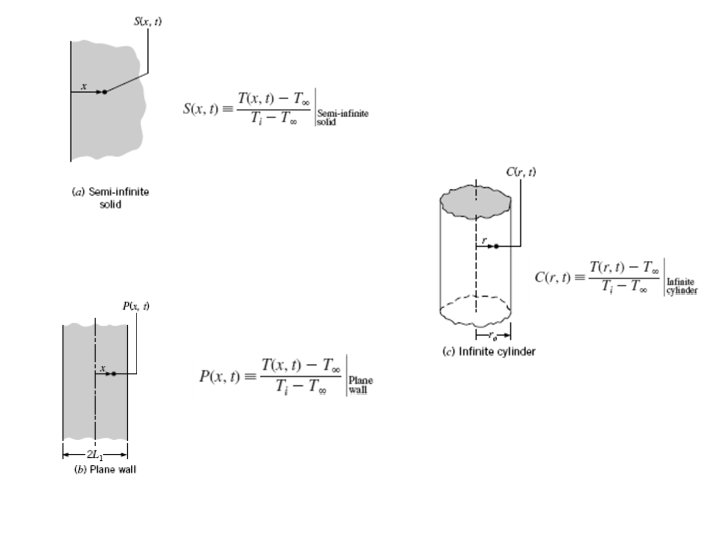
Multi-dimensional Conduction • The analysis of multidimensional conduction is simplified by approximating the shapes as a combination of two or more semi-infinite or 1 -D geometries. • For example, a short cylinder can be constructed by intersecting a 1 -D plate with a 1 -D cylinder. • Similarly, a rectangular box can be constructed by intersecting three 1 -D plates, perpendicular to each other. • In such cases, the temperature at any location and time within the solid is simply the product of the solutions corresponding to the geometries used to construct the shape. • For example, in a rectangular box, T(x*, y*, z*, t) - the temperature at time t and location x*, y*, z* - is equal to the product of three 1 -D solutions: T 1(x*, t), T 2(y*, t), and T 3(z*, t).

Transient Conduction in A Finite Cylinder



 5'0 in cm
5'0 in cm Types of connections in steel structures
Types of connections in steel structures Radial heat conduction
Radial heat conduction Heat capacity formula
Heat capacity formula Specific heat
Specific heat Heat formula
Heat formula Heat treatment calculations
Heat treatment calculations Single pipe heat exchanger
Single pipe heat exchanger Double pipe heat exchanger calculations
Double pipe heat exchanger calculations Heat loss in babies
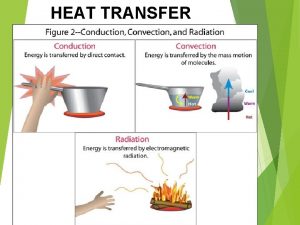
Heat loss in babies Conduction convection radiation examples
Conduction convection radiation examples We transferü
We transferü Radiation examples
Radiation examples Heat transfer types
Heat transfer types One dimensional steady state conduction
One dimensional steady state conduction Heat transfer objectives
Heat transfer objectives Heat conduction expert
Heat conduction expert Heat transfer electrical analogy
Heat transfer electrical analogy Linear heat conduction experiment
Linear heat conduction experiment What is heat transfer conduction convection and radiation
What is heat transfer conduction convection and radiation How does heat energy flow
How does heat energy flow Fourier's law heat transfer
Fourier's law heat transfer Thermal resistance formula
Thermal resistance formula Linear and radial heat conduction
Linear and radial heat conduction Conservation of energy heat transfer
Conservation of energy heat transfer Examples of conduction
Examples of conduction Heat conduction animation
Heat conduction animation Method of heat transfer
Method of heat transfer Conduction vs insulation
Conduction vs insulation Tcola
Tcola